舰用隔振橡胶超弹性力学本构模型研究

金 著，赵应龙，杨 雪

（1.海军工程大学振动与噪声研究所，武汉 430033；2.船舶振动噪声重点实验室，武汉 430033）

0 引 言

随着舰船振动噪声控制水平的提高，橡胶减振器在舰船设备上的应用也日趋普及，制作舰用橡胶隔振器所使用的橡胶材料可称为舰用隔振橡胶材料，通常具有耐油、耐盐雾、耐高温等特性[1]。由于疲劳、老化等因素的影响，隔振橡胶材料性能会逐渐降低，进而影响隔振器寿命，因此，研究橡胶隔振器的寿命特性离不开对决定其使用寿命的橡胶材料基本特性的研究[2-3]。非线性超弹性力学特性是橡胶材料最重要的基本特性之一。

对于橡胶材料和橡胶隔振器的研究已持续多年，但针对舰用隔振橡胶材料非线性超弹性力学特性的具体研究过程和数据少有报道，这对舰用橡胶隔振器的结构设计和材料选型带来了不利影响[4]。

本文结合弹性力学、超弹性体材料本构模型等相关理论，开展舰用隔振橡胶材料的单轴、平面和等双轴拉伸试验；将试验数据代入常用本构模型进行参数拟合，通过分析三种拉伸试验拟合原理、对比不同本构模型拟合效果，确定能够较准确描述舰用隔振橡胶材料应力应变本构关系的本构模型及模型参数；通过对由拉伸试验橡胶材料制作的舰用橡胶减振器开展静态仿真分析和静态试验，验证本构模型的准确性和工程实用性。

1 超弹性理论与本构模型

1.1 超弹性理论

对于橡胶类超弹性体材料，其本构模型可表述为

式中，σ为Cauchy 应力张量，F是变形梯度张量，p是静水压力，为材料的应变储能函数，C为右Cau⁃chy-Green变形张量[5-6]。

在主坐标系下，材料沿主轴方向的伸长率称为主伸长率，用λi表示，此时变形梯度张量F为

可见，只要确定应变能函数W，橡胶材料的应力应变关系，也即本构模型就可确定。

1.2 本构模型

建立橡胶材料超弹性力学本构模型的核心是寻找最合适的应变能函数表达式。

现有模型主要分两类：一类是基于分子热力学的统计模型，其优点是模型具有物理意义，缺点是模型复杂，使用不便，包括Arruda-Boyce 模型和Van der Waals 模型等；另一类是基于唯象理论的连续介质力学模型，其优点是使用灵活，可以通过设置较多参数实现对非线性和大应变材料力学行为的精确描述，缺点是缺乏物理意义以及由于模型参数较多，确定参数所需开展的试验也较多，常用模型包括：Ogden 模型、Mooney-Rivlin 模型、Neo-Hooke 模型、Yeoh 模型、多项式模型以及减缩多项式模型等[8]。

上述部分模型之间还存在相互转化关系，比如：由Ogden 模型可以导出Mooney-Rivlin 模型和Neo-Hookean 模型；多项式模型可以化为Mooney-Rivlin 模型；减缩多项式模型可以化为Neo-Hookean模型和Yeoh模型。关于常见本构模型的具体研究，可参考文献[8]。

2 舰用隔振橡胶材料拉伸试验

橡胶材料拉伸试验数据常用来拟合其本构模型，其原理是通过特殊应力状态下的拉伸试验获得主应力和主伸长率的对应关系，再选取合适的应变能函数模型，通过拟合得到应变能函数的诸参数，进而完成橡胶材料本构模型的构建。常见的拉伸试验类型有：单轴拉伸试验、平面纯剪拉伸试验和等双轴拉伸试验。

2.1 拉伸试验理论

单轴拉伸试验中，标识段橡胶材料处于只有一个主方向上存在主应力、其他两个主方向上主应力为零的应力状态，其主轴方向上的主伸长率λi和柯西主应力σi满足下式[9]：

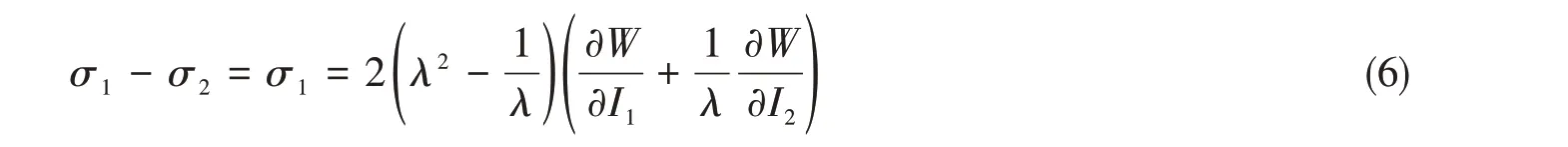
在橡胶材料拉伸试验中，通常试验得到的是标识段橡胶材料的工程主应变分量εE1和工程主应力σE1，满足下式：

该式为单轴拉伸试验的基本拟合方程。

平面拉伸试验设计目标是使试片标距段内的橡胶材料在试验过程中处于主应力分量σ3=0、由主应力分量σ1和σ2产生的纯剪应力状态，其工程主应变分量εE1和工程主应力σE1关系式为

该式为平面拉伸试验的基本拟合方程。

等双轴拉伸试验设计目标是使试片标距段内的橡胶材料在试验过程中处于两个主方向上应力相等、另一个主方向上应力为零的应力状态，其工程主应变分量εE1和工程主应力σE1关系式为

该式为等双轴拉伸试验的基本拟合方程。

2.2 拉伸试验

使用专用拉伸试验仪器及工装分别开展上述三种拉伸试验。其中，单轴拉伸试验使用哑铃状试片，平面拉伸试验使用矩形试片，等双轴拉伸试验使用齿轮形试片，每种试验均在恒温环境下使用三张相同试片重复三次，试验现场见图1。

图1 隔振橡胶材料拉伸试验Fig.1 Tensile tests of isolation rubber

试验结果经处理后如图2～4所示。

图2 单轴拉伸试验结果Fig.2 Results of uniaxial tensile test

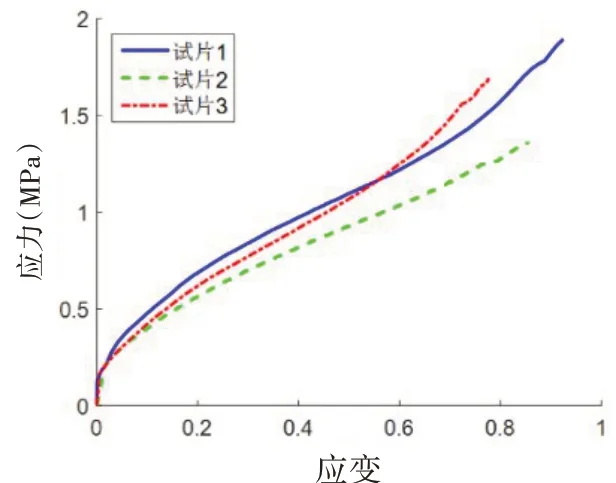
图3 平面拉伸试验结果Fig.3 Results of plane tensile test

图4 等双轴拉伸试验结果Fig.4 Results of biaxial tensile test

由试验结果可见，三种拉伸试验均表现出较高的重复一致性。对三种拉伸试验，后文中均取试片1的数据进行研究。

3 超弹性力学本构模型建模

橡胶材料常用的本构模型有十几种，根据舰用隔振橡胶材料拉伸试验数据的拟合效果选择一种适合该橡胶的本构模型对后续研究具有重要意义。

3.1 本构参数拟合

使用上一章中三种拉伸试验数据对常用的九种橡胶材料本构模型进行拟合。拟合所得本构模型的应力应变关系与测试数据的对比情况如图5所示。

3.2 本构参数选取与建模

由图5 可见，使用不同本构模型得到的拟合结果对三种应力状态拉伸试验数据的还原度各不相同，比如，对等双轴拉伸试验数据拟合效果好的，对其他两种试验数据拟合效果可能较差，也有对三种试验数据拟合效果均不太理想的。在选取合适

本构模型时，应考虑三种试验的影响权重。

单轴、平面和等双轴拉伸试验中，橡胶的主伸长率分别满足关系式[9]：

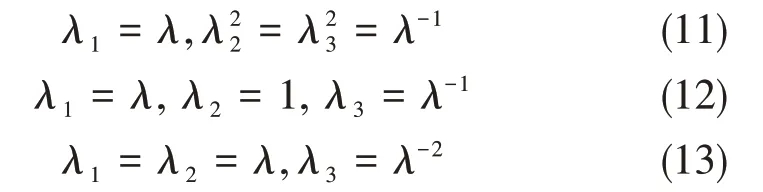
据此，可作出三种试验下橡胶材料主伸长率λ1和λ2的关系图，如图6所示。

图6 三种拉伸试验主伸长率的关系Fig.6 Relationship among the main elongation rates of three tensile tests

对于橡胶类不可压缩超弹性体材料，其一点的应变状态由主伸长率λ1和λ2即可确定，因此，图6 中λ1-λ2平面上的所有点，即为材料全部可能的应变状态之集合。而通过一个拉伸试验，则可得到该平面上的一条曲线。显然，曲线越多、线与线之间的位置关系越理想，就能越全面地描述材料的应变状态。这一原则可作为三种拉伸试验结果影响权重的定性分析依据。

可见，图6中单轴拉伸试验和等双轴拉伸试验曲线组合的位置关系最为理想，能尽可能多地覆盖平面的区域，即能够较好地描述材料的应变状态，而平面拉伸试验曲线则可认为是一种补充。

因此，在选取适合舰用隔振橡胶的本构模型时，优先考虑模型对单轴和等双轴拉伸试验数据的拟合效果。此外，在同样较好的拟合效果前提下，应优先选取参数较少、计算简便的模型。

根据上述原则，从拟合结果来看，首先排除对三种试验数据拟合效果都不好的Mooney-Rivlin 模型、Neo-Hooke 模型、二阶减缩多项式模型、一阶Ogden 模型和Arruda-Boyce 模型，剩下的四种模型拟合效果均较为理想。二阶多项式模型、Yeoh模型、二阶Ogden模型以及Van der Waals模型的模型参数分别为5、3、4、4 个，且Yeoh 模型最为简易，便于开展更深入的理论计算。因此，本文研究中选用适用于高质量高精度研究、且拟合效果较好、计算简便的Yeoh 模型（即三阶减缩多项式模型）作为舰用隔振橡胶材料本构模型。

使用Yeoh模型拟合的结果为

单位均为MPa。

4 仿真与试验验证

以某一型舰船上应用广泛的橡胶隔振器为例，对建立的舰用隔振橡胶材料Yeoh 本构模型开展验证研究。

该减振器由三部分组成：支持承、卡板和橡胶弹性体。其中卡板是减振器的金属框架，起连接基座和橡胶弹性体的作用；支持承下部包裹在橡胶弹性体中，上部与被减振设备连接。额定载荷为3000 N，额定载荷下静变形约4 mm，结构示意图如图7所示。

图7 目标橡胶隔振器结构示意图Fig.7 Structure of target rubber isolator

通过仿真计算该减振器在额定载荷作用下的变形量，并与试验数据进行对比，即可验证本构模型的准确性。

4.1 仿真计算

建立隔振器仿真模型时，橡胶材料使用前述本构模型；用捆绑约束定义橡胶和金属接触面；所有单元均使用六面体单元，橡胶单元使用C3D8RH，金属单元使用C3D8H；边界条件为下表面固定，支持承只允许垂向移动；载荷条件为支持承上表面施加垂直向下的3000 N载荷。

仿真计算得到的减振器垂向静变形云图如图8 所示，支持承上表面控制点的力位移特性曲线计算结果如图9所示，其中在3000 N载荷下，垂向变形量为3.97 mm。

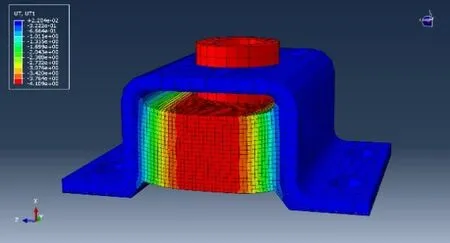
图8 橡胶隔振器垂向位移云图Fig.8 Cloud chart of rubber isolator’s vertical displacement

图9 橡胶隔振器位移—载荷曲线Fig.9 Displacement-load curve of rubber isolator

4.2 试验验证

对使用拉伸试验中橡胶材料制成的28 只舰用橡胶减振器开展垂向静变形测试，测试结果如表1所示。

表1 橡胶隔振器静变形试验结果Tab.1 Measurement results of the static deformation of rubber isolators

从测试结果可见，28 只橡胶隔振器在额定载荷下垂向静变形的均值为4.02 mm，与仿真计算结果3.97 mm 相比，误差仅为1.24%。可见，本文确立的超弹性本构模型及其参数，能较好地满足舰用隔振橡胶材料应力应变本构关系仿真计算需求，具有较高的准确性和工程实用性。

5 结 论

本文通过橡胶类超弹性体材料本构模型理论和拉伸试验研究，确立了舰用隔振橡胶材料本构模型，并通过仿真分析和试验，验证了模型的准确性。主要结论如下：

（1）Yeoh 模型适合用于描述舰用隔振橡胶材料超弹性力学特性，且具备模型参数少和计算资源占用少的优点。

（2）本文确定的Yeoh 模型参数可作为舰用橡胶减振器橡胶材料超弹性力学参数，能够较精确地描述橡胶减振器的静态力学性能。

（3）对三种拉伸试验数据，应优先考虑本构模型对单轴和等双轴拉伸试验数据的拟合效果。

本文的研究成果可为舰用隔振橡胶材料超弹性力学特性分析和舰用隔振器设计计算等研究提供材料数据和方法思路，具有一定的工程指导意义。