船体裂纹板双轴非比例低周疲劳载荷下累积塑性行为研究

2023-02-04邓军林涂雯羚董大伟邱圣临卢瑞涛

船舶力学 2023年1期

邓军林，涂雯羚，许允，董大伟，邱圣临，卢瑞涛

（1.北部湾大学机械与船舶海洋工程学院，广西钦州 535011；2.中国船级社广州审图中心，广州 510235）

关键字：船体裂纹板；双轴低周疲劳；非比例载荷；累积塑性；疲劳寿命

0 引言

结构承受交变载荷所产生的疲劳损伤，一直是船舶、海洋结构面临的问题，而多轴载荷下结构疲劳寿命的分析研究则是问题的关键[1]。现有的相关研究成果集中于在单轴交变载荷作用下的结构断裂问题，而对于实际海况中，船舶结构发生的总体破坏大多是在多轴及不同相位载荷影响下，船体梁的纵向构件承受不同程度的交变载荷作用，导致危险断面处的纵向构件发生轴向弯曲甚至扭转，危险断面的承载能力随之不断降低，最终引起船舶结构的总体破坏[2-3]。因此，船体结构疲劳寿命的准确评估对于保证船舶结构在营运过程中的安全具有重要意义。

通常，多轴低周疲劳船体板在交变载荷的作用下会受到低周疲劳裂纹扩展的断裂破坏以及因结构材料延展性丧失而产生的累积塑性破坏。根据早期的事故分析研究，Fujita等[4]发现，船体结构变形产生的累积塑性损伤，导致船体结构在足够的交变载荷下发生断裂失效，并且累积塑性变形随循环加载次数的增加而增大；随后，刘应华等[5]通过大量实验后明确指出，结构在承受应力水平较大的循环载荷时，会进入塑性变形不断累积或不断反复的破坏过程，并最终导致结构破坏，其破坏形式分别对应于累积塑性变形破坏或低周疲劳破坏；黄震球在1995年前后就已十分重视对船体在循环载荷下累积塑性破坏的研究，进行了大量的相关理论分析及模型实验研究工作[6-7]，进一步强调累积塑性破坏准则在船舶总体强度分析中的关键性作用；任慧龙[8]开展了基于累积塑性破坏的船体结构极限强度研究工作，也指出了累积塑性的影响作用。当船体产生的塑性变形的累积值超过某一限定值后，会引发船体局部结构低周疲劳裂纹的萌生、扩展并最终导致结构的总体断裂破坏。

事实上，早在20世纪中旬，就已有学者提出了船舶结构塑性损伤的概念，但并没有得到充分的重视[9]。1970 年，Coffin[10]指出累积塑性应变会造成额外的损伤，并可能导致疲劳寿命缩短[11]。1990 年，Mansour等[12]提到在计算塑性设计方法和损伤率时，应考虑塑性累积损伤的影响。近年来，研究人员对低周疲劳失效与累积塑性损伤相互作用进行了大量实验和理论研究。Satyadevi[13]提出的断裂准则中明确指出，对于低周疲劳寿命必须考虑累积塑性的影响；同时，Xia[14]在进行不对称循环应力试验中发现，结构材料会产生累积塑性变形，造成结构内部损伤，进而降低低周疲劳寿命。随后，Kang[15]对SS304 不锈钢进行了一系列低周疲劳与累积塑性损伤作用实验，结果表明，最终的疲劳失效寿命和累积塑性应变在很大程度上取决于平均应力、应力幅和应力比，并提出了考虑累积塑性影响的疲劳失效模型来预测疲劳寿命。然而，现有的实验结果大多为单轴循环应力载荷下低周疲劳与累积塑性的相互作用。因此，对于多轴非比例低周疲劳载荷下的船体结构，更应考虑累积塑性损伤这一重要影响因素。

对于多轴疲劳载荷作用下的应力应变关系，尚德广[16]等对45号钢材料的薄壁管试件进行了拉-扭联合作用的疲劳实验研究，整理了不同载荷形式下的拉压分量滞回线与扭转分量滞回线；Qu等[17]则总结了拉-扭多轴疲劳实验中Q235b钢圆管型拉扭试件及其焊接试件在比例加载和90°非比例加载下的循环应力应变曲线，并指出在非比例实验中，圆管试件存在着明显的循环强化效应；Foletti等[18]在研究多轴低周疲劳短裂纹扩展行为时，得到了不同应力幅作用下的稳定应力应变闭环曲线。实际上，学者们对多轴疲劳循环应力应变关系的研究大多是以拉-扭的圆管试件为实验对象，而对于双轴非比例拉伸的板材试件的研究则寥寥无几。

本文将通过实验研究分析船体斜裂纹板在双轴非比例载荷下累积塑性与低周疲劳的耦合作用。重点探究在不同应力比R、双轴应力比λ和相位差φ时，裂纹尖端塑性应变的累积效应以及应力应变相互变化关系。在此基础上，通过建立的双轴非比例低周疲劳载荷下基于累积塑性的裂纹板低周疲劳寿命预测模型对试件的疲劳寿命进行分析。研究可为准确评估在非比例双轴低周疲劳作用下，累积塑性对船体板疲劳寿命的影响提供重要依据。

1 理论分析

船体薄板构件一般处于平面应力状态，二轴低周疲劳载荷作用下，裂纹板尖端的弹塑性应力应变本构关系是由应力应变曲线结合弹性理论、塑性理论求得，考虑增量物理方程[19]（广义霍克定律）和塑性流动规则与可塑性表面的关系，其表达式如下：

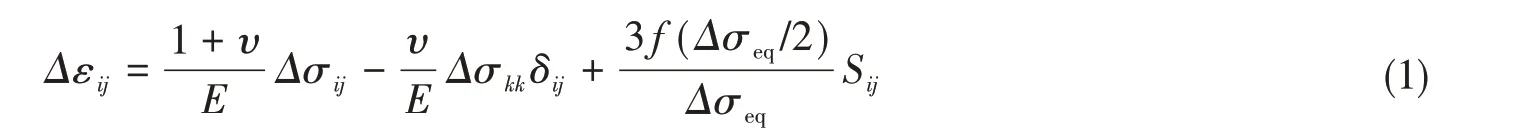
式中，Δεij和Δσij是应变和应力张量分量的增量，E是杨氏模量，υ是泊松比，ΔSij和Δσeq通过下式计算获得：

采用Chaboche非线性硬化模型[20]作为本构模型参数，材料屈服函数为

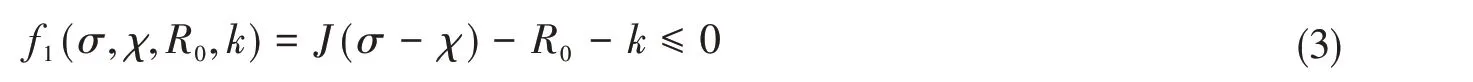
式中，χ是非线性运动硬化变量，R0是各向同性硬化变量，k是初始半径的屈服面，J是von Mises距离内的偏应力空间，并且，

其中，σ'和χ'分别是σ和χ的差值。

塑性流动法则为

非线性运动硬化χ和各向同性硬化变量R0可以表示为

式中，C1、a1、C2、a2、b、Q是材料常数，通过实验来确定，ε̇p是累积塑性应变率。

根据讨论Chaboche 模型的文献[21]，塑性应变与累积塑性应变之间的微分关系，在n+1 循环中累积塑性应变可以表示为

式中，dεp,n+1是第一个n+1 个载荷循环后裂纹尖端等效塑性应变增量，可以根据Newton-Raphson 迭代法通过n+1个载荷循环后裂纹板裂纹尖端应力-应变关系来获得。将式（7）代入文献[22]中的Newton-Raphson 迭代法，可获得n+1个循环后的裂纹尖端塑性应变增量dεp,n+1。另外，也可以获得相应的塑性应变增量。依次更新相应的参数，可以求得在第i个循环中相应的塑性应变增量。因此，双轴低周疲劳载荷下裂纹板裂纹尖端在n+1个载荷循环的塑性应变增量Δεp可以表示为

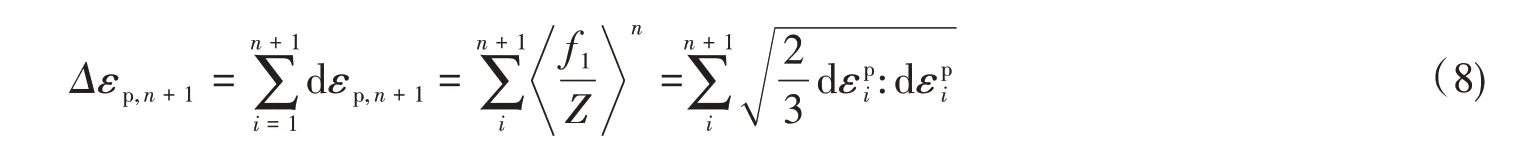
通过式（8）可获得第n+1 次载荷循环后的塑性应变增量Δεp，n+1。依次更新相应参量，即可求得每次对应循环下的塑性应变增量。方程（8）即是在n+1 个载荷循环后裂纹板裂纹尖端累积增量塑性应变值的表达式。

双轴非比例低周疲劳载荷下，裂纹板von Mises等效塑性应变根据文献[23]通过使用X轴和Y轴方向的累积塑性应变分量ɛp，x和ɛp，y获得。

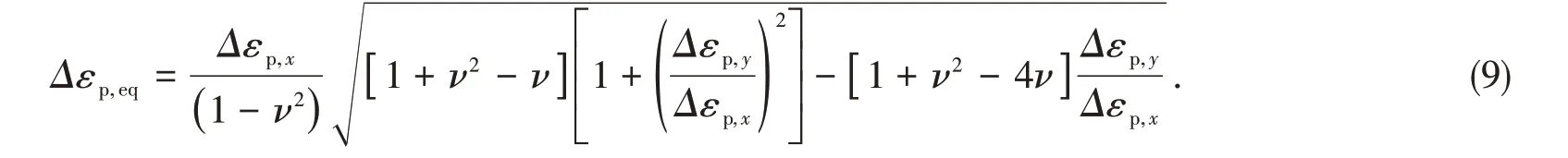
将根据方程（8）获得的对应载荷循环下的累积塑性应变作为双轴非比例低周疲劳载荷下裂纹板在X轴和Y轴方向的塑性变形分量代入方程（9），即可获得在双轴非比例低周疲劳载荷下裂纹板在相应载荷循环后裂纹尖端von Mises等效塑性应变。

2 实验研究

2.1 实验装置

本次实验所用的试件材料为Q235 钢，其化学成分为（以重量%计）：C-0.17，Mn-0.49，Si-0.23，P-0.026 和Si-0.025。为了更好地研究非比例载荷下双轴低周疲劳裂纹扩展中的累积塑性现象，选用常规十字型试件，其长度和宽度分别为190 mm和76 mm，试件整体板厚为8 mm，中部圆形区域板厚削减为3.8 mm。两臂交界处设置椭圆形圆角，减小交界处的应力集中，以确保试件中心产生较高且均匀的应变区域。试件采用放电法加工，并设置长度为8 mm的预制裂纹，其几何尺寸如图1所示。实验装置使用MTS 505.60 四通道电液伺服，并利用计算机控制伺服液压执行器；所有实验均采用双轴应力控制，并在室温下进行正弦波形周期加载，加载频率为1 Hz。试件的实验数据通过高精度应变采集裂纹扩展区域内水平和垂直方向上的实时应变值。

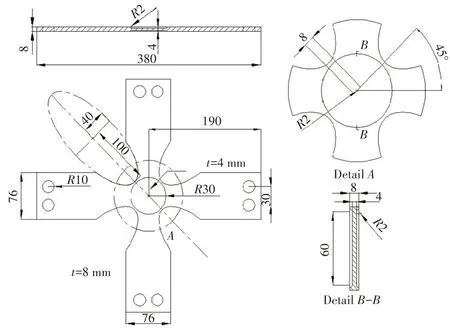
图1 双轴低周疲劳试验十字型试件Fig.1 Biaxial low-cycle fatigue test cruciform specimen

图2为试验加载工装示意图。在助动器的安装过程中，使用水平仪和铅垂线辅助安装，保证两作动器的水平和垂直，以此来实现加载力的平面正交性。疲劳试件和实验工装通过销轴实现紧密联接，工装①和工装②通过螺栓固定于相互正交的工字梁框架内，工装③、④则分别安装在水平方向和垂直方向的2 个作动头上。测试时我们选用合适的载荷大小及平均应力，考虑不同相位差、双轴应力比和应力比对双轴非比例低周疲劳累积塑性现象的影响。

图2 实验装置及裂纹尖端处应变片放大图Fig.2 Magnified view of the experimental setup and strain gauge at the crack tip

本文采用双轴低周疲劳载荷为拉伸载荷，在载荷设计中以水平应力分量σx和垂直应力分量σy作为基准，通过控制变量法，考虑了应力比R、双轴应力比λ和相位差φ三种不同因素，以此来探究各种载荷形式对裂纹尖端累积塑性现象的影响。通过单调拉伸试验，得到了Q235 钢的基本应力-应变曲线，如图3 所示。从图中可以看出，Q235 钢的弹性模量和屈服强度实测值分别为206 GPa和430 MPa。

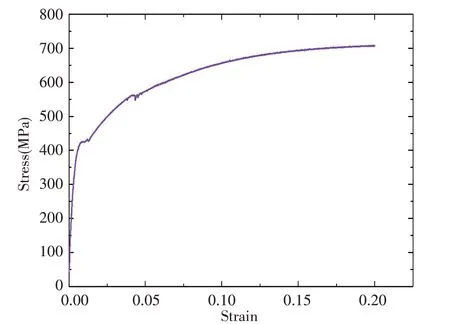
图3 Q235钢在室温条件下进行单轴拉伸试验得到的应力应变曲线Fig.3 Stress-strain curve of Q235 steel obtained by uniaxial tensile test at room temperature

2.2 实验结果与讨论

2.2.1 裂纹尖端应力应变场

为了研究裂纹尖端应力应变行为，图4 分别给出了不同应力比、多轴比以及相位差下裂纹尖端应力应变迟滞回线。

图4（a）表明，随着循环次数的增加，应力应变曲线逐渐趋于稳定，稳定后的迟滞回线其应变水平随着R的增加而增大。这主要是因为R越大，对应的平均载荷应力值也更大，所以引起的应变水平更高。但是稳定后迟滞回线的应变值仍在不断累积，出现了明显的循环弱化。图4（b）为不同相位差下双轴应力应变曲线。由于主应力方向持续变化，循环应力应变曲线比等比例载荷（φ=0）的迟滞曲线更加饱满。在φ小于90°时，循环应力应变曲线变化不是很明显，从图中可以看出，随着φ的增加，应力应变水平缓慢增加；然而当φ持续增加到90°时，迟滞曲线的应力水平稳定上升，同时应变水平也逐渐升高。然而，当相位差φ为180°时，循环迟滞曲线的应变出现了大幅度衰减，其原因是这一相位差下疲劳载荷的合应力值较小，且其载荷路径与等比例加载下合力大小相同、方向相反。因此，在不同相位差下双轴拉-拉载荷下应力应变曲线与等比例载荷下有明显差异。从图4（c）可以看出，随着双轴应力比λ的增加，迟滞回线所形成的圆环越发有扁平趋势，但双轴应力比对最初应力范围的影响呈正相关。随着双轴应力比λ的增加，应变范围逐渐变小，迟滞回线出现了顺时针旋转的趋势。当λ为0.5 时，此时Y方向垂直应力更大，即主应力方向与预制裂纹的角度更大，因此其循环应力应变曲线的应变水平和应力范围都是最大的。这一点进一步体现了在不同双轴应力比的二轴低周疲劳载荷下主应力方向发生改变所带来的影响。然而，随着λ的增加，载荷的主应力方向逐渐偏向于裂纹的平行方向，相应的循环应力应变水平也越来越低。因此，裂纹尖端的应力应变水平与预制裂纹垂直方向的载荷幅值密切相关，而平行方向的载荷值对应力应变水平影响较小。Lee[24]在研究不同双轴应力比载荷作用下中心穿透裂纹铝合金板的二轴低周疲劳裂纹扩展行为时，观测到由载荷主应力方向改变所引起的裂纹扩展方向偏转现象。

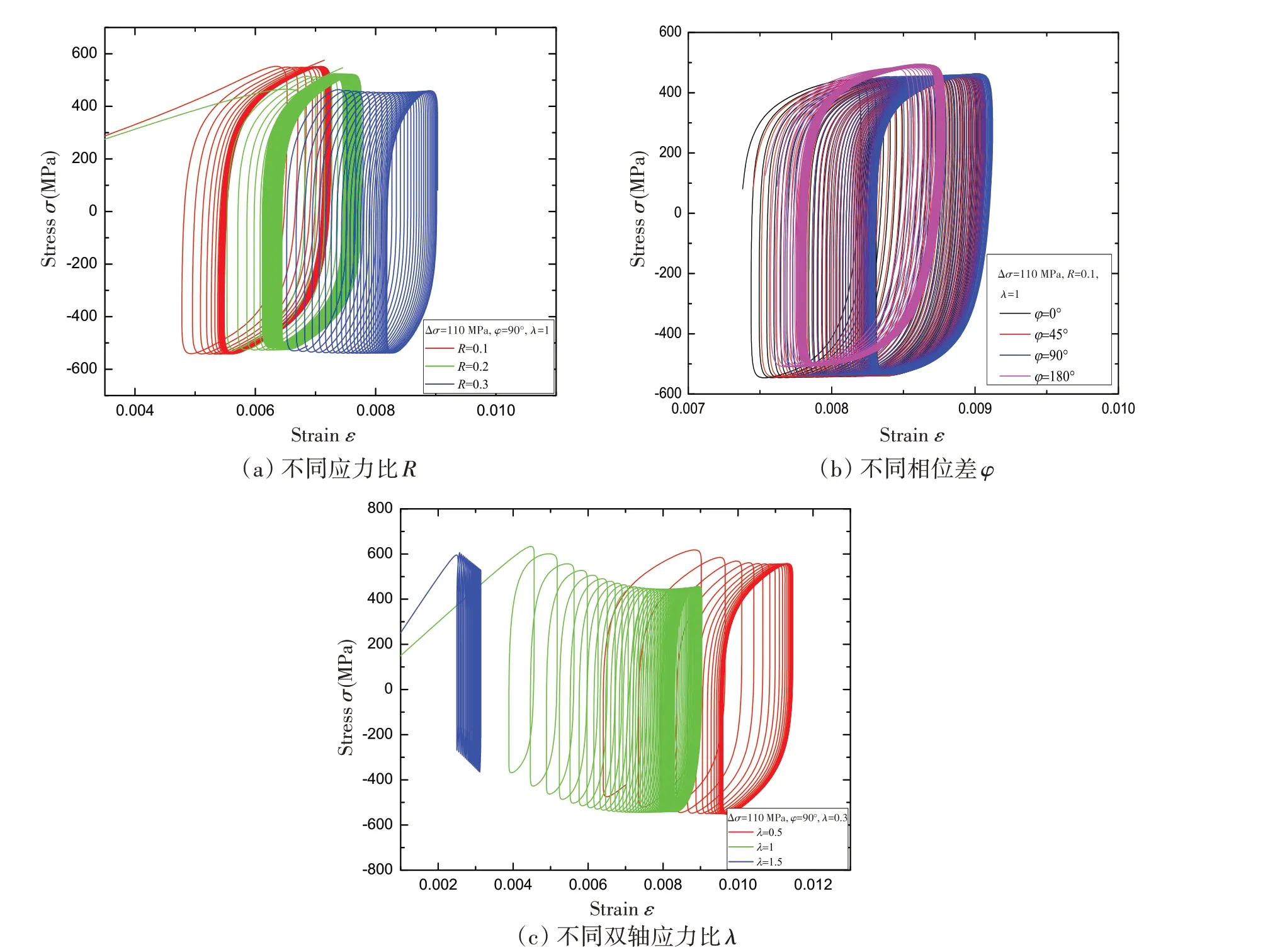
图4 不同双轴非比例低周疲劳载荷作用下裂纹板应力应变迟滞回线Fig.4 Stress-strain hysteresis loops of cracked plates under different biaxial non-proportional low-cycle fatigue loadings

2.2.2 累积塑性变形分析

通过uTek 动态数据分析系统得到了各工况下应变值与加载循环次数的关系曲线，如图5 所示。根据结果可知，在各工况载荷下水平方向上的应变和垂直应变均出现了塑性累积现象，每个循环周期内的最大应变值是逐渐累积增长的。特别地，在非比例加载过程中，由于载荷的主应力方向持续旋转改变，使得裂纹尖端局部区域受压产生负的压缩应变值，对45°方向上的合应变测量值造成了很大的影响。

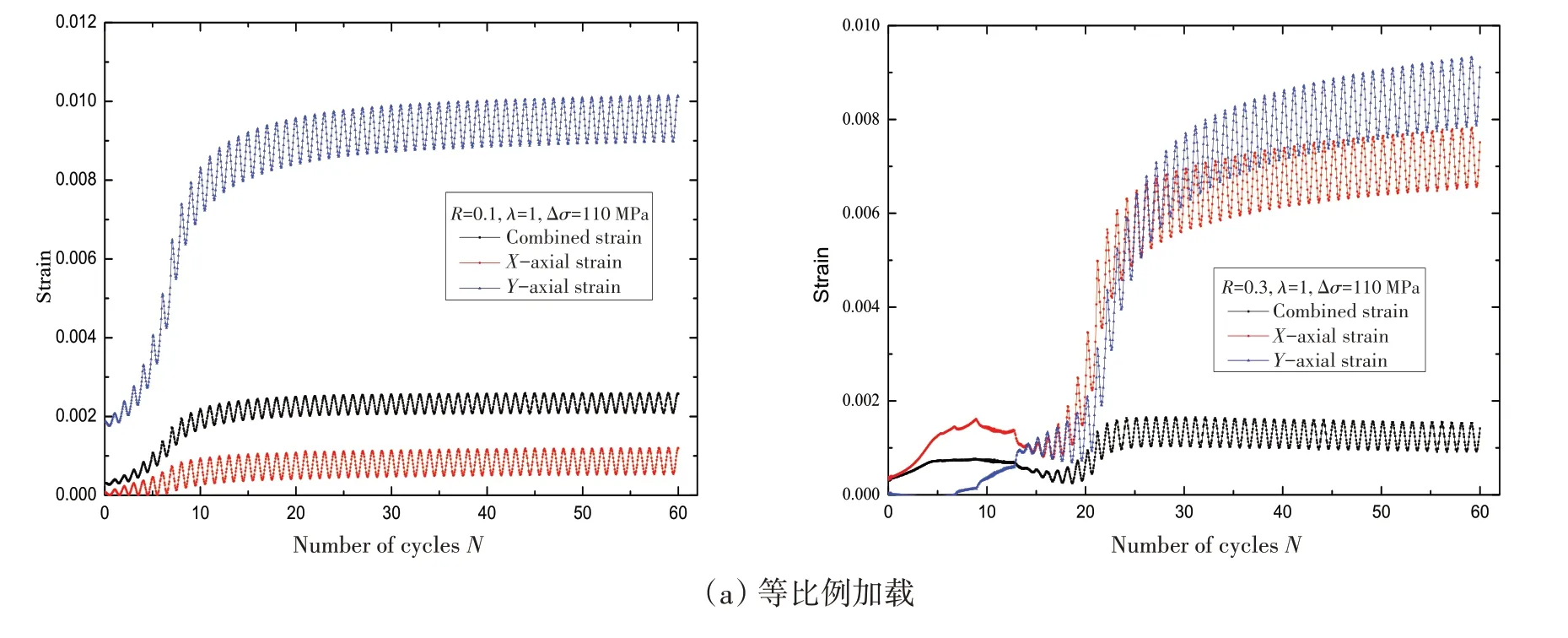
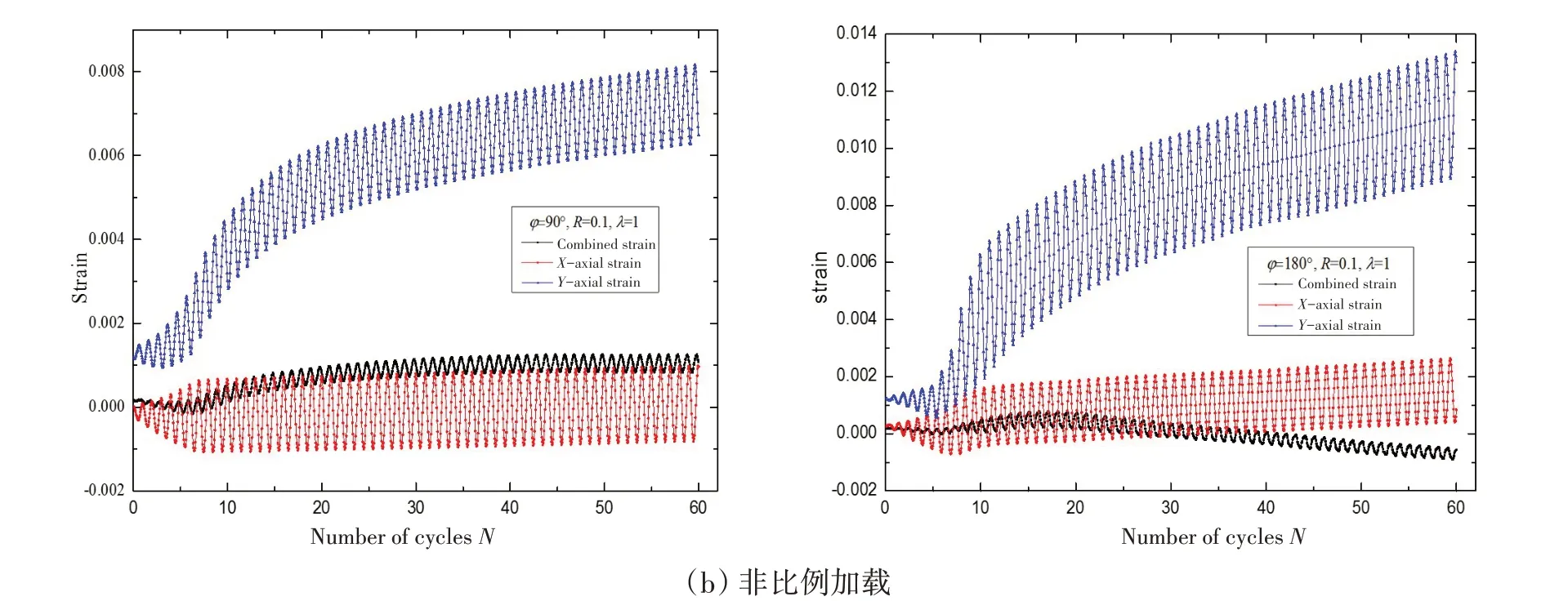
图5 典型工况下试件应变的变化关系曲线Fig.5 Strain variation curves of specimens under typical loading conditions

为了研究裂纹扩展过程中不同载荷条件下裂纹尖端累积塑性应变的变化情况，在实验中采用控制变量方法，仅改变双轴低周疲劳载荷中的应力比R、双轴应力比λ和相位差φ。经过一系列的实验测量，在不同应力比、双轴应力比以及不同相位差载荷作用下的裂纹尖端塑性应变增量Δεp与循环次数N的对应关系曲线如图6所示。

图6 不同双轴非比例低周疲劳载荷作用下裂纹板累积塑性应变率关系曲线Fig.6 Accumulative plastic strain rate curves of cracked plates under different biaxial non-proportional low-cycle fatigue loadings

由图6（a）显示的实验结果可以看出，在非比例循环载荷作用下，裂纹尖端的累积塑性应变随应力比的增加呈正相关。这是因为随着应力比的增长，试件裂纹尖端的应力水平越大，塑性应变的累积率也越高。说明塑性累积率与试件裂纹尖端的应力水平相关。图6（b）显示，在非比例双轴低周疲劳循环载荷作用下，不同双轴应力比的累积率与循环次数的关系呈下降趋势。这是由于不同双轴应力比通常对应着不同的水平应力分量和垂直应力分量。但相位差的存在，导致其合应力的方向时刻发生改变，因此裂纹尖端的应力水平会随垂直应力的大小发生改变，当λ=0.5 时，其垂直应力水平最大，即其合应力方向偏向Y轴，随着λ的增加塑性应变累积率逐渐降低，实验结果也符合这一规律。图6（c）表明在不同相位差作用下累积塑性应变率随相位差的增加而逐渐增大。但对于每个条件下累积塑性应变率与循环次数关系曲线，可以看出曲线由最开始达到峰值后缓慢降低，这是由于试件在进行双轴拉-拉实验时，在裂纹萌生初期加载状态不稳定，到后续扩展区域加载状态稳定增长，直至后期试件发生断裂失效，塑性应变累积率急速下降。

实验结果表明，随着加载的持续，塑性应变累积率由最开始不稳定到逐渐减低直至非零的稳定值。Tchankov[25]在研究COD 应变范围与循环次数的对应关系时，也得出了类似的结论。很明显，在双轴非比例低周疲劳实验中，试件都出现了塑性累积现象。

2.2.3 低周疲劳与累积塑性相互作用

为了探究非比例加载条件下低周疲劳和累积塑性相互作用，对Q235 钢在不同应力比、双轴应力比和相位差条件下进行了双轴拉-拉载荷试验，直至发生低周疲劳失效。图7所示为累积塑性应变与循环次数的关系，从图7（a）可以看出，在双轴应力比及相位差恒定时，对于不同应力比的加载情况，累积塑性应变随循环周期的增加由最初的不稳定状态到急剧增加，增加速率先增加后逐渐下降，直至达到非零的稳定值。图7（b）为等比例加载下不同应力比累积塑性应变与循环次数的关系图。可以清晰地观察到，累积塑性应变随循环次数的增加而增加，并且对于不同应力比，随着应力比的增大累积塑性也增加到稳定值。结果表明，累积塑性应变及其增长率随应力比的增加而单调增加。这是由于随着应力比增加，材料所产生的累积损伤逐渐增大，导致材料抵抗变形的能力慢慢丧失，从而最终影响累积塑性应变的增长率快速上升，直到后期试件疲劳失效，累积塑性增长率值达到稳定。这与Deng等[9]进行单轴AH32 钢试验所得结果类似。说明在双轴非比例低周疲劳拉-拉载荷实验中，应力比对船体裂纹板的累积递增塑性应变影响较为明显。

图7 不同应力比下累积塑性与循环次数关系Fig.7 Relationship between accumulative plasticity and cycles at different stress ratios

图8 为比例与非比例两种加载情况下，不同双轴应力比对累积塑性应变与循环次数的影响关系曲线图。在两种加载条件下，累积塑性应变及其增长率都随循环次数的增加而增加直至稳定状态。在不同双轴应力比下，累积塑性应变随λ的增大而逐渐减小。这是由于在进行双轴实验时，选用具有45°预制斜裂纹的十字型试件，双轴施加载荷的主应力方向逐渐偏向于裂纹的平行方向，导致相应的塑性应变水平越来越低，从而延缓其累积塑性增长率。然而，在等比例加载下，从图8（b）可以发现，当λ=0时，即为y方向上的单轴加载，其主应力方向与预制裂纹呈现45°夹角；当λ≠0时，其主应力方向与预制裂纹之间的夹角远小于45°。即在单轴载荷下，其累积塑性应变值是最大的，进而其累积塑性应变与增长率比λ≠0时大得多。由此可以看出，裂纹尖端的累积塑性现象与双轴比λ密切相关，双轴的载荷可以转化为主应力与初始裂纹间夹角，平行方向的载荷值对应力应变水平影响较小。

通过实验结果得到的累积塑性应变，用以表示低周疲劳与累积塑性损伤相互作用，从图9可以看出它与相位差的关系。结果表明，累积塑性应变随相位差的增加而增加，在其他条件不变的前提下，具有相位差的累积塑性应变都小于φ为0°时等比例加载的值。这是由于相位差的存在，非比例载荷的主应力方向会持续变化，没有一个固定的主应力方向，对于不同相位差所对应的加载路径也会随循环次数的增大而发生改变，从而导致其累积塑性应变水平增加缓慢。因此，相位差的增加对累积塑性应变的值略有影响，这与主应力路径循环载荷下发生的累积塑性损伤相对应。

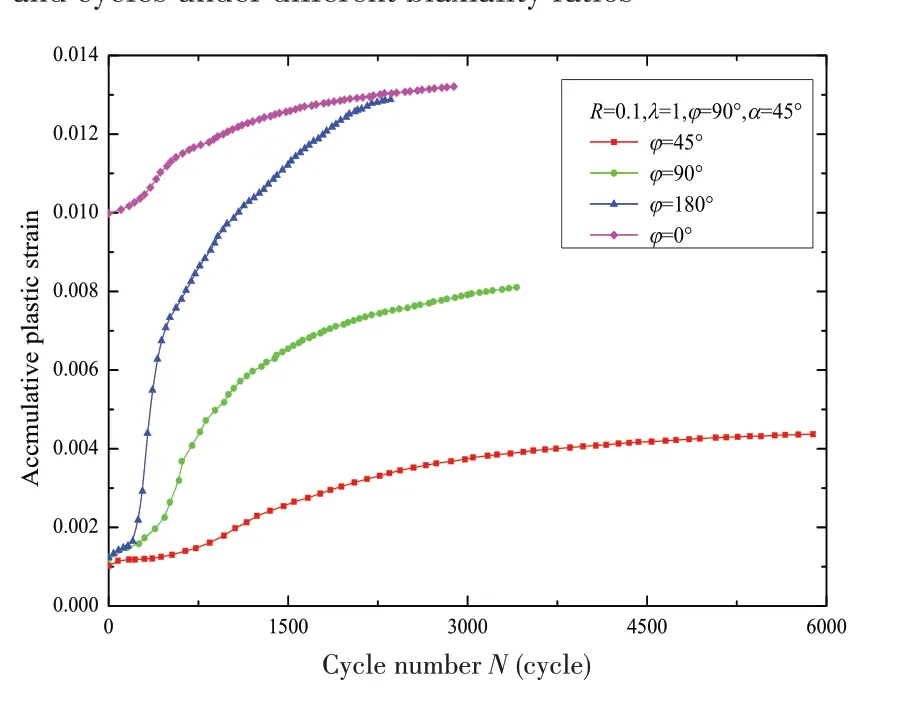
图9 不同相位差下累积塑性与循环次数关系Fig.9 Relationship between accumulative plasticity and cycles under different phase differences

2.3 疲劳寿命

将方程（9）求得的双轴非比例低周疲劳载荷下裂纹板累积塑性应变代入经典Manson-coffin 方程[26]即可获得裂纹板双轴非比例低周疲劳寿命。为了验证本文提出的双轴非比例低周疲劳寿命预测模型的可靠性，与实验结果进行了对比分析。图10～11 分别为不同相位差和双轴应力比下材质为Q235钢的十字形试件低周疲劳寿命关系曲线。

图10 显示了不同相位差下Q235 钢试件双轴非比例低周疲劳寿命对应关系。可以发现疲劳寿命随相位差的增加而减小，在应力比R为0.1时，相位差为45°的疲劳寿命最长。这意味着在非比例循环应力中产生的累积塑性损伤会导致额外的疲劳损伤，从而缩短疲劳寿命。当相位差和双轴应力比不变时，应力比的增加使疲劳寿命有下降趋势，此时材料的失效主要受较大的累积塑性应变控制，说明Q235 钢的疲劳寿命随应力比的增加而降低。因此，Q235 钢的非比例循环应力产生累积塑性应变，从而降低了试件的疲劳寿命，在不同应力比及相位差的循环应力作用下的低周疲劳研究中应考虑这种相互作用。

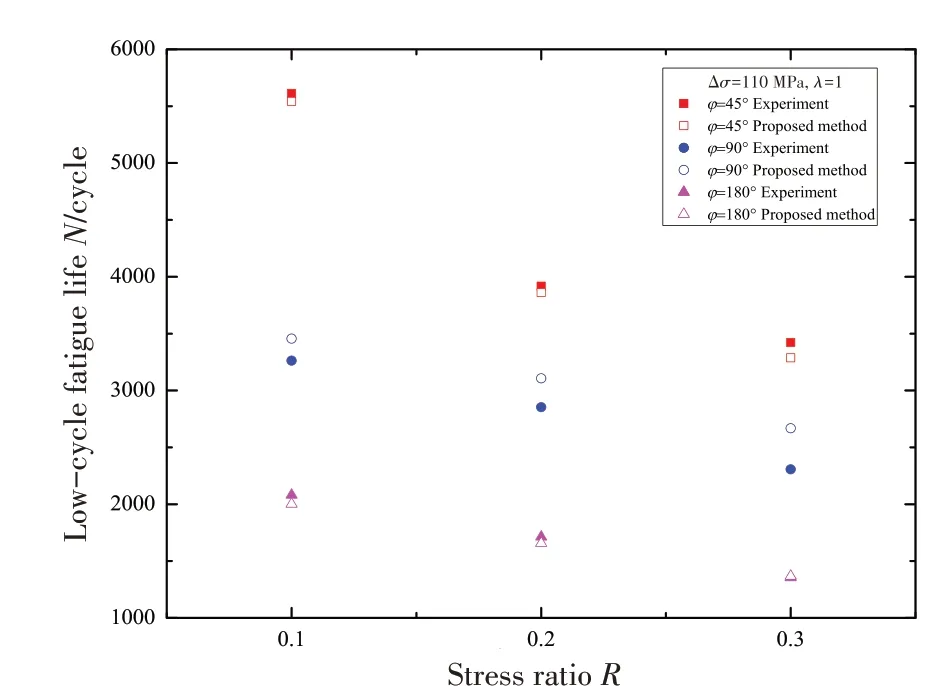
图10 不同相位差下试件双轴非比例低周疲劳寿命对应关系Fig.10 Relationship of biaxial non-proportional low-cycle fatigue life of specimens with different phase differ⁃ences

图11表明在双轴非比例循环应力下，不同双轴应力比λ对Q235钢试件双轴非比例低周疲劳寿命的影响更为显著。从图11中可以看出，在相同应力比R下，低周疲劳寿命随双轴应力比λ的增加而单调减小。由于双轴应力比λ的增加引起的累积塑性应变较大，从而导致疲劳寿命相应较小。并且，在相同双轴比λ下低周疲劳寿命随应力比R的增加而单调降低。当双轴比λ越大时，在双轴非比例循环应力下会产生较大的累积塑性变形，从而降低了试件的双轴非比例低周疲劳寿命。因此，双轴比λ较大时，Q235钢试件的双轴非比例低周疲劳寿命明显受累积塑性应变的不利影响。

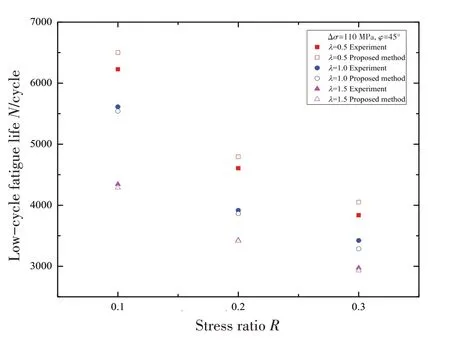
图11 不同双轴比下试件双轴非比例低周疲劳寿命对应关系Fig.11 Relationship of biaxial non-proportional low cycle fatigue life of specimens with different biaxiality ratios

实验结果表明，双轴非比例循环应力下产生的累积塑性应变对Q235钢的低周疲劳寿命影响十分显著，会大大降低疲劳寿命。因此，考虑低周期疲劳与累积塑性损伤的相互作用效应，能够更好地描述Q235 钢的低周期疲劳寿命。图10～11 表明，本文提出的基于累积塑性变形的双轴非比例低周疲劳寿命预测模型在不同相位差、双轴比下预测值基本能接近实验值，说明本文提出的预测模型能对双轴非比例低周疲劳寿命进行评估。