矩形窗口球阀流体控制性能研究

2023-02-03杨恒虎刘柏圻廖静王伟波

机床与液压 2023年1期

杨恒虎，刘柏圻，廖静，王伟波

(1.重庆川仪调节阀有限公司，重庆 401121；2.重庆川仪自动化股份有限公司技术中心调节阀研究所，重庆 400707)

0 前言

现代自动化工艺系统中，阀门起流体控制的作用，是管路系统中不可或缺的控制装置[1]。球阀是集结构简单、经济效益高、密封严密可靠、开关方便等优点于一身的阀门[2-3]，其销量占据各类阀门总销量的50%以上。而球阀中应用最广的是O形球阀，只起开关作用。为优化球阀的控制性能，众多学者开发了V形窗口球阀，并运用仿真技术对其性能进行研究。张皓男等[4]、吴相和唐铃凤[5]运用数值仿真技术对DN50 V形球阀内部流场及流量控制特性进行研究，并根据仿真结果，优化了阀门性能。焦喜娟[6]对DN50 V形窗口球阀的流通面积进行理论分析，并用有限元软件研究了结构参数对空化的影响；毛伟[7]也运用仿真手段对V形球阀的空化特性进行了深入研究。石柯[8]、马传京[9]采用数值仿真方法与实验研究方法，分析球阀稳态与瞬态工况下阀门开度及阀芯开启速度对内部流动特性的影响，结果表明利用CFD软件可以预测球阀启闭过程瞬态及动态特性。目前，有限元仿真结果与流量试验结果误差较小[10]，使得仿真技术成为阀门行业研究的主要手段。为拓展球阀的应用工况，本文作者提出一种矩形窗口球阀，分析其结构特点，并采用有限元仿真技术对口径为DN50矩形窗口球阀的流场控制性能与流量控制性能进行研究，为工业自动化控制设备的研究与发展奠定了基础。

1 矩形窗口球阀

1.1 矩形窗口球阀结构

矩形窗口球阀与O形窗口球阀整体结构基本相同，但球芯窗口的开口形式为矩形，其整机结构示意见图1。球芯窗口形状见图2，其流道上下面为平行平面，左右两侧为对应口径的圆弧流道面，因其开口形状近似为矩形，称为矩形窗口球阀；图中球芯窗口宽度D为25 mm。

图2 球阀窗口形状Fig.2 Opening shape of ball valve

1.2 矩形窗口球阀流量控制原理

矩形窗口球阀为旋转类阀门，通过球芯旋转，控制阀座圆形流道与球芯上的矩形流道相交形成的流通面积大小，实现阀门流量控制。图3展示了矩形窗口球阀在开度30%～100%时，球芯窗口与阀座流道相交形成的流通面积，即图中阴影部分。因球阀结构密封的需要，阀座流道通径大于球芯流道通径，致使球阀开启过程中存在较大死区。DN50球阀的有效开启开度为30%～100%，因此后续仿真分析开度也为30%～100%。

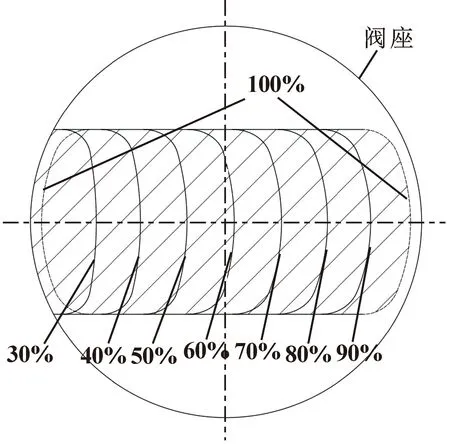
图3 流通面积示意Fig.3 Flow area

2 流量控制理论

流量控制性能是指阀门流量与相对开度的变化关系，而阀门的流量系数表征着阀门流通能力，其值只与阀门自身结构有关，与介质等其他参数无关，因此，阀门的流量控制性能也常用流量系数与相对开度的变化关系来表征。目前调节阀常用的控制性能为线性与等百分比特性。线性特性是指调节阀单位开度变化下的流量系数变化量相等，可由式(1)计算。等百分比特性是指调节阀单位开度下的流量系数的变化量与此开度流量系数的比值相等，可由式(2)计算。

(1)

(2)

式中：Lm为开启行程；Lmax为最大行程；Cm为行程Lm时的流量系数；Cmax为行程Lmax时的流量系数；R为流量变化率，通常取50。

根据相关文献研究结果，阀门流量系数可通过两种方式计算得到：流通面积计算流量系数与流量试验计算流量系数。文献[11]中得到阀门流量系数Kv与流通面积的关系式(3)，而国际通用流量系数为Cv值，其与Kv值关系为式(4)，联立式(3)(4)可得阀门流量系数与流通面积的关系：

(3)

Cv=1.156Kv

(4)

(5)

式中：A1为管道流通面积，m2；A2为节流处流通面积，m2；Kv为5～40 ℃的水在105Pa压差下，每小时流过调节阀的立方米数，m3/h；Cv为15.56 ℃的水在6.894 8 Pa压差下，每分钟流过调节阀的体积流量。

式(5)揭示了阀门流通能力与流通面积的基本关系，即流通能力随流通面积的增加而增大，但相应公式的理论推导建立在节流处流线平直的简单节流孔且节流过程中无能量损失，不能真实反映阀门的流量系数。

文献[12]规定了阀门试验条件下的流量系数的计算公式，公式中的各参数值通过流量试验得到。因此，试验条件下计算得到的流量系数更准确。

(6)

式中：Q为体积流量，m3/h；ρ1/ρ0为相对密度，当介质为15 ℃的水时，值为1；Δp为上、下游取压口的压力差，kPa；N1为数字常数0.086 5。

3 矩形窗口球阀流场控制分析

3.1 计算区域的网格划分与边界设置

为获取矩形窗口球阀内部流场控制的详细情况，运用有限元仿真软件对阀门不同开度下的介质流动状态进行模拟。限于篇幅，此处仅选取口径为DN50、窗口宽度为25 mm的矩形窗口球阀，开度在30%、60%、100%时的流场分布分析。依据文献[13]所述，三维建模时取管道长度为2D，阀后管道长度为6D(D为管道直径)。参阅文献[1,14]中的仿真模型，为节约计算资源，提高计算效率，结合矩形球阀结构对称的特点，采用一半模型进行模拟分析，流体域模型如图4所示。对流体域模型采用结构化与非结构化网格相结合的方法进行网格划分[15]，即阀前后管道划分为六面体网格，阀体区域划分四面网格，网格交界面处节点对齐，总网格数量50万左右。网格划分结果如图5所示。

图4 开度100%流体三维模型Fig.4 Three-dimensional fluid model of valve opening at 100%

图5 开度100%网格模型Fig.5 Mesh model of valve opening at 100%

因阀门流量系数与介质参数等无关，此处为提高求解收敛速度，采用标准的k-e湍流模型，采用近壁面函数，模拟固体边界对流体流动影响；边界条件采用压力进口1 MPa及压力出口0 MPa，湍流强度为5%，水力直径设置为0.05 m，并将介质设置为液态水，其密度为998.2 kg/m3，动力黏度为0.001 003 Pa·s。

3.2 流体速度分布图

图6(a)(b)(c)分别为矩形窗口球阀在30%、60%、100%开度下，对称面上速度分布。可知：矩形窗口球阀在开启过程中，在球芯处形成“S”形流道；随着开度不断增大，“S”形流道角度逐渐变小，当开度为100%时，流道变为直通。从球芯流道形状变化可知，随开度的增大，球阀的流通能力逐步增强。从对称面速度分布图可知：3个开度的高流速区均出现在球芯进口处，球芯出口处也存在较高流速，但相较于进口，有所降低。3个开度的最大流速分别为32、43、63 m/s，与开度呈正相关关系。因此，矩形窗口球阀的流量随开度的增大而增大。

图6 对称面速度分布

3.3 流体流线分布图

图7(a)(b)(c)分别为矩形窗口球阀在30%、60%、100%开度下，介质内部流线分布。可见：介质在球芯窗口与前阀座流道相交形成的流通孔处汇聚，随之与球芯流道壁面形成撞击，最后再汇聚通过球芯窗口与后阀座流道相交形成的流通孔，流出阀门。其中，30%、60%开度下，介质将在球芯流道内形成涡流，极大地扰乱了介质的流动状态。此外，介质在通过阀芯后，在阀后一段管道内也形成巨大涡流，且30%开度比60%的规模更大；而开度为100%时，整个管道流线平直，已无大型涡流产生。涡流的产生极大地增加了介质流动阻力，降低阀门流通能力。从开度30%、60%、100%的介质流线分布可知：随着球阀开度的增加，介质流动状态趋于平稳，流通能力逐渐增强。

图7 介质流线分布Fig.7 Distribution map of pathline：(a)opening at 30%；(b)opening at 60%；(c)opening at 100%

经过对比分析发现，图6与图7所示速度分布与流线分布，与文献[8]中非简化模型仿真所得的XY截面的速度分布图与迹线分布图基本保持一致，证实了在一定的误差范围内采用文中简化模型仿真的准确性。

3.4 流体压力分布图

图8(a)(b)(c)分别为30%、60%、100%开度下，对称面上各处压力随流动方向的压力值分布。可见：不同开度下的阀门进出口处压力值趋于定值，表明进出口介质流动已达到稳定的流动状态，阀前后进出口管道长度合适。在阀芯处，存在明显的压降过程，且随着开度的增大，压降规律逐渐发生变化。当阀开度为30%时，在阀芯处形成明显的两级压降，且球芯进口与出口处的压降量基本相当。当阀开度为60%时，也存在比较明显的两级压降，但介质压力在球芯进口处已经降至0.2 MPa左右，在球芯出口处，压力更是降至-0.2 MPa，形成负压；介质过球芯后，压力逐渐升高至0 MPa；此开度下，阀芯进口处压降量大于出口处压降量。当开度100%时，已无明显的两级降压特征，在球芯进口处压力迅速降至-0.8 MPa，在阀芯出口压力恢复至-0.5 MPa左右，随着介质流动压力恢复至设置的0 MPa。

分析结果表明：虽然矩形窗口进出口流通面积相同，但随着开度的增加，球芯进口处节流降压效果要明显强于球芯出口处的节流降压效果，导致球阀在开启过程中，由两级降压过渡到一级降压。此外，100%开度下阀前管道介质压力0.6 MPa，与设置的1 MPa相差较大，而开度30%与60%时的压力几乎与设置的进口压力1 MPa相同。这表明随着开度增大，压力能转变动能的量在不断增加，转化效率逐步提高，流量逐渐增大。

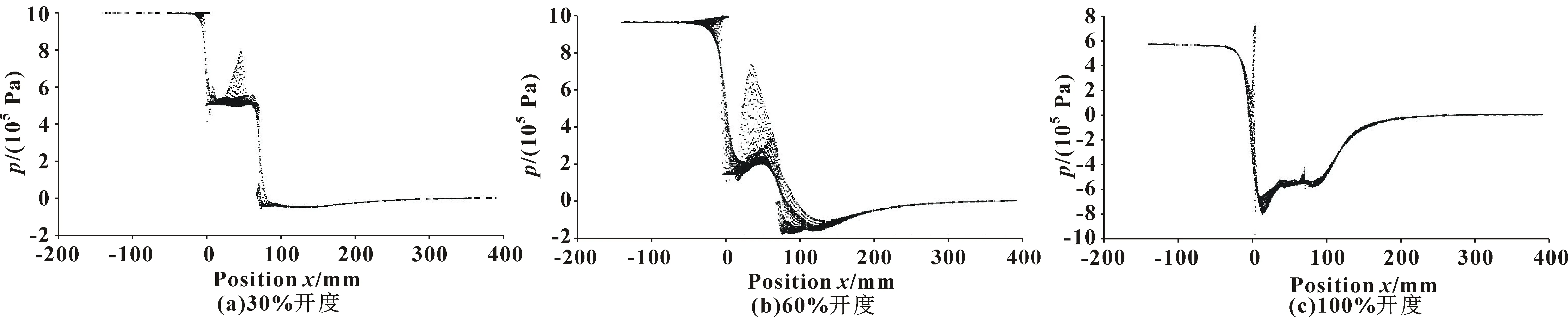
图8 对称面压力分布

4 矩形窗口球阀流量控制分析

4.1 矩形窗口球阀流通面积分析

研究的球阀通径仍为DN50，此处取仿真分析的矩形窗口宽度D的范围为5～45 mm，并且窗口宽度每增加5 mm，测试矩形窗口球阀的调节特性。因DN50球阀的有效开启开度为30%～100%，因此，仿真分析开度取30%、40%、50%、60%、70%、80%、90%、100%。

利用二维绘图软件，测得不同窗口宽度下，矩形窗口球阀30%～100%开度下的流通面积，如表1所示。

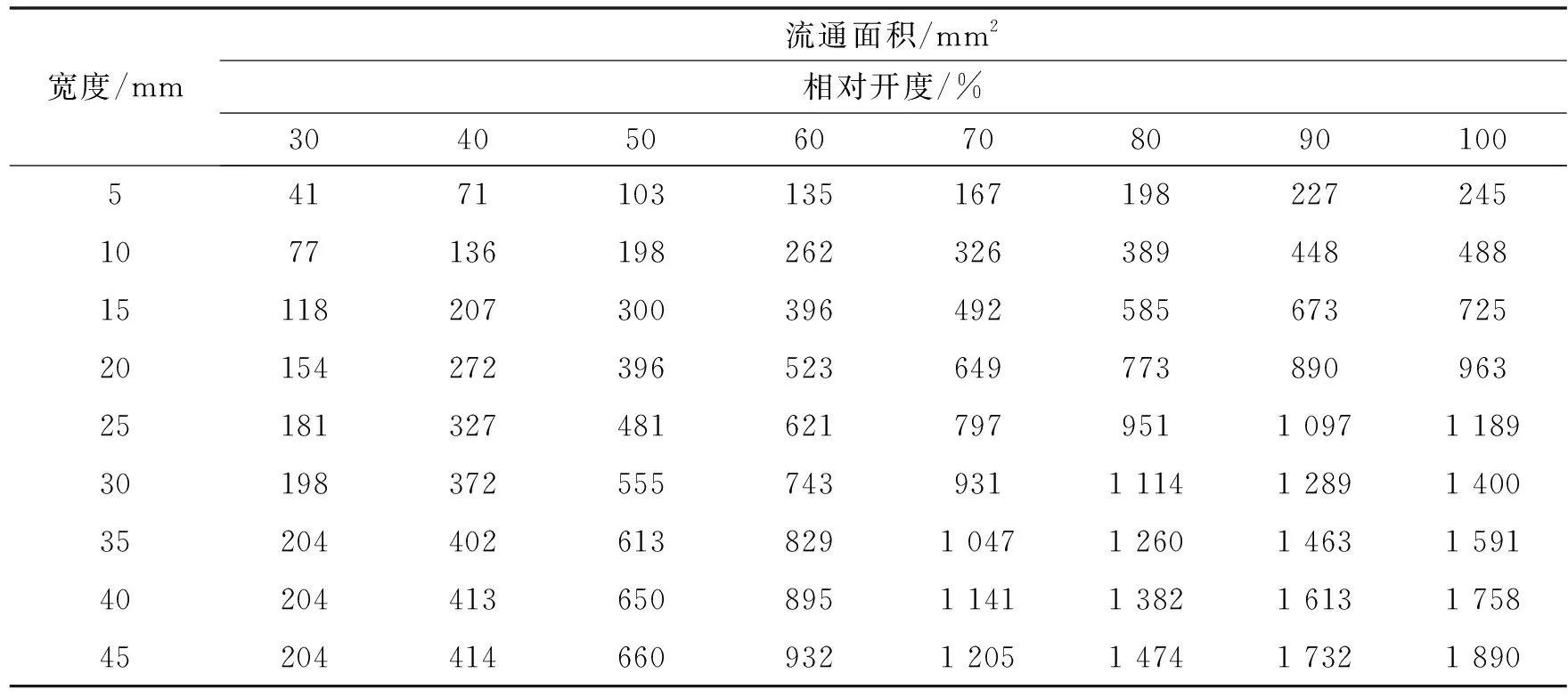
表1 矩形窗口球阀流通面积Tab.1 Flow area of rectangular-opening ball valve

可知：随着窗口宽度的增加，矩形窗口球阀100%开度的流通面积逐渐增加，但增长量逐步减小，这是由矩形窗口的两侧边为圆弧边决定的。对于其他开度也存在流通面积随宽度增加而增加的普遍规律。但对于小开度30%，在窗口宽度达到35 mm后，此开度下的流通面积不再随宽度的增加而增加，此时的流通面积由矩形窗口的圆弧边与阀座圆形通径相交形成，为球阀结构所能达到的最大流通面积，窗口宽度已不能控制流通面积的大小，这也是球阀作为调节阀的局限性。

图9展示了不同窗口宽度的矩形窗口球阀，各开度与100%开度的流通面积比值随相对开度的变化关系。可见，比值与相对开度呈现近似直线的变化规律。这表明，对于同一窗口宽度的矩形球阀，流通面积随开度的增加基本相等。此外，随着窗口宽度的增加，曲线斜率逐渐增加，这是由于矩形窗口两边为圆弧边所致；但整体上，各窗口宽度的球阀变化曲线基本重合，表明矩形窗口球阀的流通面积随相对开度的变化规律基本相同。

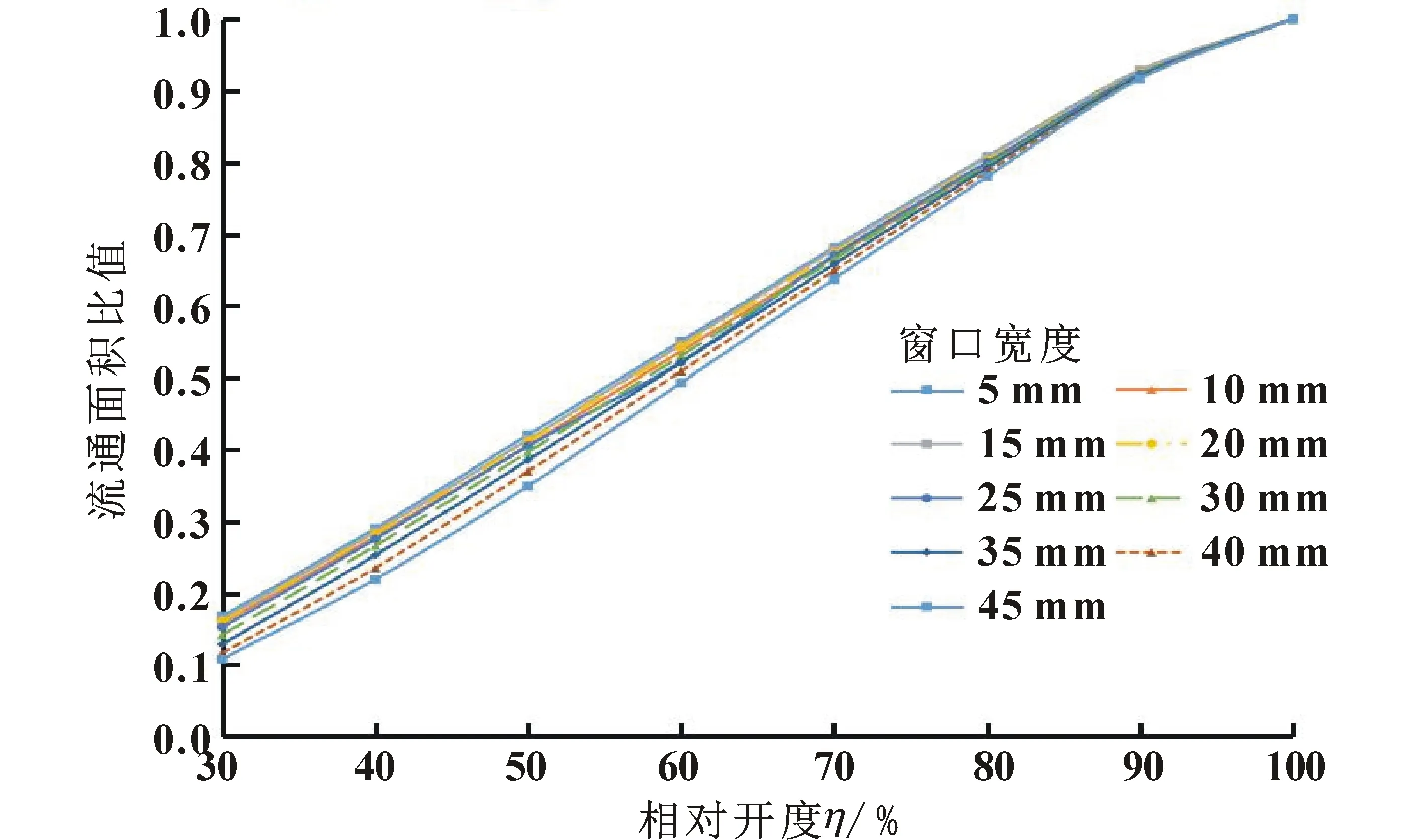
图9 流通面积比与开度变化曲线Fig.9 Change rules of flow area ratio with valve opening

4.2 矩形窗口球阀流量控制曲线分析

采用有限元仿真软件，对矩形球芯窗口不同开度下的介质流动进行模拟，读取式(6)计算所需的压差及流量，并计算得表2所示的矩形窗口球阀各开度的模拟Cv值。可知：Cv随窗口宽度或相对开度的增大而增大，与流通面积的变化趋势保持一致。当窗口宽度达到35 mm后，30%开度时的Cv值将不再随宽度的增加而增加，这也与流通面积的变化规律相同。

表2 矩形窗口球阀模拟Cv值Tab.2 Simulated Cv value of rectangular-opening ball valve

将不同窗口宽度球阀各开度与100%开度的Cv值比值与相对开度的变化关系绘制于同一张图，可得图10所示的不同窗口宽度的矩形球阀的流量控制曲线。各条曲线不再重合为一条曲线，呈现线性与等百分比曲线共存现象，具有与流通面积不同的变化规律。分析图10可得：(1)所有曲线位于流量变化率为50∶1的理论线性曲线以下，表明矩形窗口球阀的调节特性不能设计为常规的线性特性；(2)窗口宽度为5～15 mm时，球阀的调节特性基本呈现线性特性，与流通面积变化趋势相同，具有较好的相关性；(3)窗口宽度大于等于20 mm时，球阀的调节特性均呈等百分调节特性，且随着窗口宽度的增加，流量变化率逐渐增大，这表现出与流通面积不同的变化规律；(4)窗口宽度为25～30 mm时，特性曲线与流量变化率为50∶1的理论等百分比曲线重合度较高，可以作为常规等百分比特性的调节阀使用。