RV减速器柔性因素对动态传动误差影响分析

2023-02-03贾吉帅周建星曾群锋李高铠王宏伟张荣华

机床与液压 2023年1期

贾吉帅，周建星，曾群锋，李高铠，王宏伟，张荣华

(1.新疆大学机械工程学院，新疆乌鲁木齐 830047；2.西安交通大学现代设计及转子轴承系统教育部重点实验室，陕西西安 710049)

0 前言

RV(Rotate Vector)减速器由一级渐开线行星轮传动和二级摆线行星轮传动组成，因具有传动效率高、抗冲击能力强、寿命长、传动精度高和回差小等优点，而被广泛应用于精密回转机构中。传动精度一直以来都是RV减速器的技术核心和研究重点，减速器传动精度会直接影响装备的运行精度和工作表现，而系统中各构件受载变形是产生传动误差的主要原因之一，因此将接触和支承弹性变形这样的柔性因素对传动误差的影响量化研究对减速器的设计和优化具有重要工程意义。

目前，国内外学者针对RV减速器传动精度进行了一系列研究。研究主要集中于静态传动精度研究和动态传动特性研究。静态层面的研究主要通过几何法[1-2]，如何卫东等[3]以传动精度、回差、扭转刚度、传动效率和承载能力作为约束条件，提出了机器人用RV减速器中摆线齿轮的修形方案。关天民等[4-5]将承载能力作为目标函数，得到了重载摆线齿轮轮齿修形量的优化方案。随后LIN等[6]基于齿面接触定量分析了不同修形组合引起的传动误差。REN等[7]通过调整摆线齿廓上5个关键点的位置来设计修形间隙曲线的修形方法，用以提高摆线针轮传动的承载能力和传动精度。这些学者在静态几何层面探究了摆线齿轮齿形因素对减速器静态传动精度的影响。动态传动精度方面，韩林山等[8-9]推导并验证了涵盖齿形误差、装配误差和装配间隙的减速器非线性运动微分方程，并进行了传动误差对装配误差的灵敏度分析。在此基础之上XU等[10-11]提出了一种轴承-摆线针轮传动的广义动力学模型，在考虑摆线齿轮副间隙和径向间隙的情况下，分析了该传动机构的特性和动态接触响应。这些研究考虑了减速器中复杂的几何结构关系，在动态层面对减速器的传动精度进行了较深入的研究。RV传动系统中的振动特性、动应力及扭转刚度是传动精度的重要影响因素，对此也开展了大量研究[12-13]。王辉等人[14]分析了摆线齿轮多齿啮合的动态过程和齿面接触应力的分布规律。吴素珍等[15]结合有限元分析技术，得到了减速器曲拐轴承各滚针的应力状态。杨玉虎等[16]通过有限元分析了RV减速器扭转刚度特性，得出轴承刚度是影响整机扭转刚度变化的主要因素。这些研究从根源处揭示减速器动态传动误差的成因，扩展了RV减速器分析的维度，但是关于接触和各支承处弹性变形对减速器传动误差的影响没有横向展开，进行量化对比分析。

综上所述，RV减速器的几何结构和运动关系非常复杂，分析难度较高。以往学者对该类型减速器的误差影响因素的研究大多集中于齿形、装配和制造误差对传动精度的影响以及零部件强度、刚度的有限元分析，关于支承及齿轮接触变形对减速器传动精度影响的深入分析未见文献报道。鉴于此，本文作者建立计入支承柔性和Hertz接触刚度的BX40E减速器线性动力学模型，提取减速器齿轮的动载荷、输出转速和动态传动误差信号，讨论负载转矩、输入转速与上述物理量的关系，分析齿轮接触和支承处弹性变形对转动误差的贡献，最后量化评价柔性支承及接触刚度对传动精度影响的灵敏度。

1 传动误差研究方法

RV减速器轮齿接触变形和轴孔支承处弹性变形是传动误差产生的根源之一。本文作者在以往学者研究的基础之上，探究了减速器内各处支承柔性以及轮齿接触刚度对减速器传动精度的影响，研究流程可分为3个模块，即动力学建模模块、误差贡献量分析模块和动态传动误差灵敏度分析模块，如图1所示。

图1 动态传动误差影响流程

首先，对减速器进行几何建模和动力学建模，在此过程中，为考虑接触和支承处弹性变形对传动误差的影响，采用Palmgren公式和Hertz接触理论确定系统的支承刚度和接触刚度。然后，通过该模型提取齿轮动载荷、动态传动误差和输出转速信号，统计分析输入输出信号对应关系，通过对比已有文献结论，验证动力学模型的合理性。继而分析一、二级齿轮接触变形及支承柔性变形对传动误差的贡献量。最后，使用有限差分法计算BX40E减速器动态传动误差对各柔性因素的灵敏度，并对结果进行比较分析。

2 RV传动系统动力学建模

2.1 RV传动系统参数

以BX40E减速器为研究对象，其结构简图与几何模型如图2所示，各齿轮基本参数如表1所示。

图2 BX40E结构简图与几何模型Fig.2 Diagram and geometric model of BX40E reducer

表1 减速器齿轮基本参数Tab.1 Basic parameters of the gear system

减速器包含渐开线行星齿轮传动机构I、摆线针轮行星传动机构II及行星架输出机构Ⅲ。减速器工作时，运动从太阳轮输入，通过啮合传至行星齿轮，进行一级减速。太阳轮顺时针方向旋转，行星轮及曲柄轴整体在公转的同时逆时针自转，自转运动又带动摆线齿轮作偏心运动，针齿与摆线齿轮啮合使它围绕针轮轴线公转的同时并顺时针方向自转，自转最终通过曲柄轴传递至行星架输出机构，完成输出。

2.2 坐标与模型参数设置

文中建立了计入支承和啮合处弹性变形的RV传动系统平移-扭转耦合多自由度线性动力学模型，如图3所示。

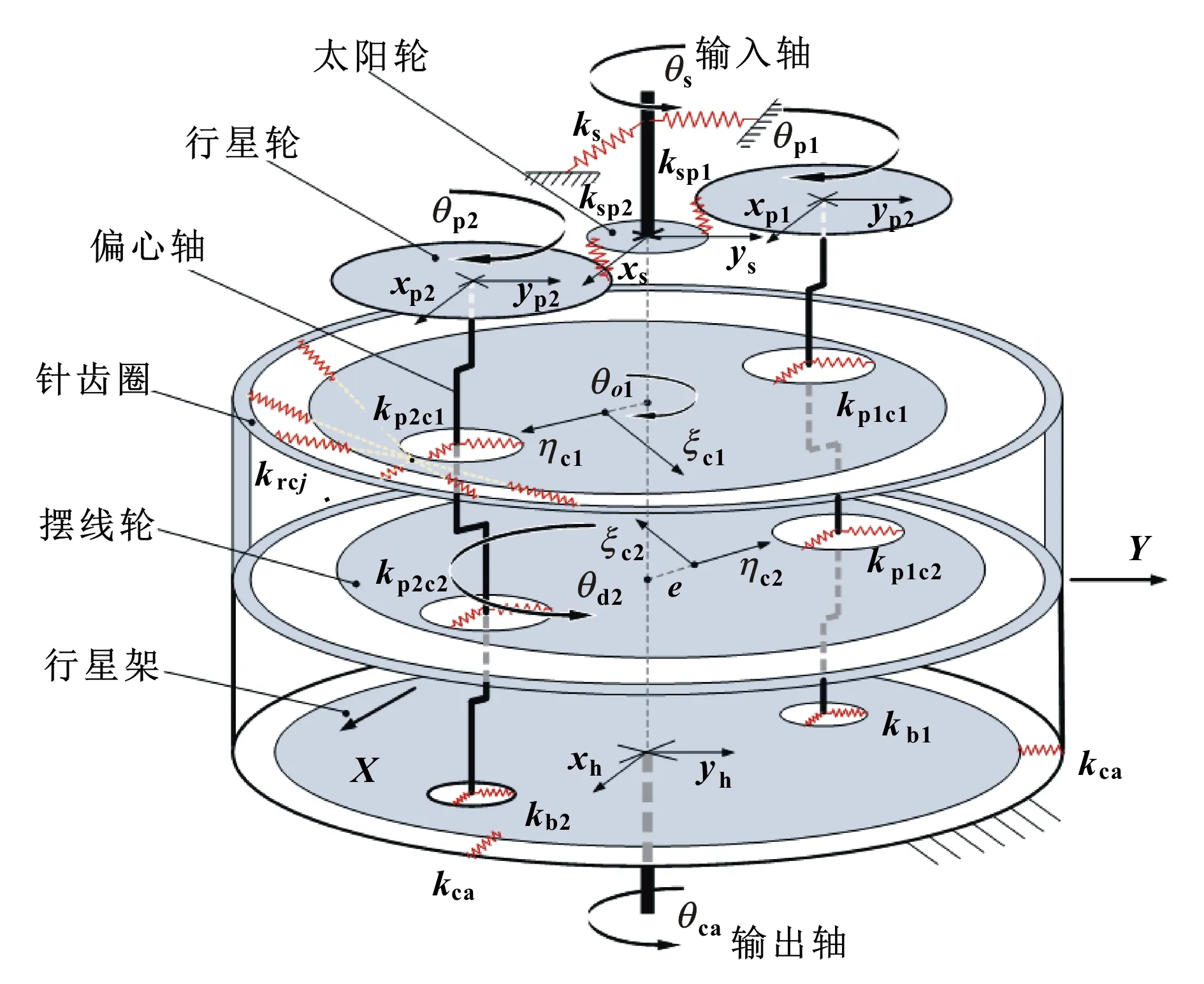
图3 RV减速器动力学模型Fig.3 Dynamic model of RV reducer

模型构建时取针齿圈中心O为原点，水平方向为X，竖直方向为Y建立全局坐标系。定义摆线齿轮的理论质心Oc为原点，以摆线轮的偏心方向为ηcj轴，沿其公转角方向转动90°为ξcj轴，建立摆线齿轮的局部动坐标系。使摆线齿轮在起始位置处时局部动坐标与全局坐标方向一致，e为摆线齿轮的偏心距，Rb为摆线齿轮节圆半径，Ra为太阳轮与行星轮的中心距。定义Φi=2π(i-1)/2 (i=1,2)为行星架上曲柄轴孔的相对位置，定义Ψj=(j-1)π(j=1,2)表示摆线齿轮理论质心Oc的相对位置。

图3中，ks和kpi分别表示太阳轮轴的支承刚度和第i(i=1,2)个行星轮轴的支承刚度，通过悬臂梁受力时的挠曲变形量来确定；kbi、kca和kpicj分别为曲柄轴与行星架输出盘轴孔间的支承刚度系数、行星架输出盘与针齿壳间的支承刚度系数和第i(i=1,2)个曲柄轴与第j(j=1,2)个摆线轮轴孔间的支承刚度系数。刚度系数通过Palmgren公式来确定[8]，如下式所示：

(1)

(2)

式中：Ei、υi分别为接触材料的弹性模量和泊松比；l为两弹性体接触线长度；F为接触弹性体的载荷。

图3中，kspi代表太阳轮与第i个行星轮的接触刚度，krcj为第j个摆线齿轮与针齿圈间的接触刚度，轮齿接触采用Hertz接触模型，如图4所示。

图4 摆线齿轮啮合接触模型Fig.4 Meshing contact model of cycloid gear

由图4可以看出：齿轮的啮合过程可以等效为两质体的相互接触，考虑材料阻尼，广义的Hertz接触力可以表示为

(3)

(4)

(5)

式中：r1、r2分别为两相接触体的曲率半径；Ei、υi分别为接触材料的弹性模量和泊松比。

2.3 RV减速器系统动力学模型

根据胡克定律，支承处的作用力可表示为支承刚度与位移的乘积。令太阳轮在支承处的微位移为xs、ys和θs，则太阳轮的支承作用力可表示为

Fsx=ksxs

(6)

Fsy=ksys

(7)

令行星轮轴的3个微位移分别为xpi、ypi和θpi-θp,摆线齿轮的3个微位移分别为ηdj、θdj-θc和θOj-θp,则摆线轮对曲柄轴的支承作用力可表示为

Fjix=kpicj(xpi+scjix

(8)

Fjiy=kpicj(ypi+scjiy

(9)

其中:scjix和scjiy为摆线齿轮在支承处的微位移，其表达式为

scjix=Ra(θdj-θcsin(θc+Φi-ηdjsin(θp+Ψj

(10)

scjiy=-Ra(θdj-θccos(θc+Φi+

ηdjcos(θp+Ψj

(11)

令行星架的3个微位移分别为xca、yca和θca-θc，行星架对曲柄轴间的支撑作用力可表示为

Fcaix=kbi(sbix+xpi

(12)

Fcaiy=kbi(sbiy+ypi

(13)

其中:sbix和sbiy分别为行星架输出盘在支承处x、y方向上的微位移，其表达式为

sbix=-xca+Ra(θca-θcsin(θc+Φi

(14)

sbiy=-yca-Ra(θca-θccos(θc+Φi

(15)

行星架对针齿壳间的支撑作用力可表示为

Fcax=kcaxca

(16)

Fcay=kcayca

(17)

齿轮之间的啮合作用力的值可以表示为轮齿接触刚度与齿轮在啮合线方向上位移的乘积。所以太阳轮与行星轮的啮合作用力可表示为

Fspi=kspi(ss+spi

(18)

其中：ss和spi分别为太阳轮和行星轮在啮合线上产生的微位移，可表示为

ss=xscosα+yssinα

(19)

spi=-xpicosα-ypisinα-rp(θpi-θp

(20)

摆线齿轮与针齿的啮合作用力可表示为

Fjk=kcjrkscjrk

(21)

其中：scjrk代表摆线齿轮与针齿在啮合线上的微位移，其表达式为

scjrk=ηdjcosαjk-Rb(θdj-θcsinαjk

(22)

结合上述运动部件的受力分析、根据牛顿力学理论，建立第二级摆线齿轮传动的运动微分方程如式(23)[8]所示：

(23)

式中：ms、mp、mc和mca分别为太阳轮、行星轮、摆线齿轮和行星架输出盘的质量；Js、Jp、Jc和Jca分别为太阳轮、行星轮、摆线齿轮和行星架输出盘的转动惯量；rs和rp分别为太阳轮和行星轮的基圆半径；α和αjk分别为第一、二级齿轮传动的压力角；ωp和ωc分别为行星架的理论角速度；Tout为负载扭矩。

将减速器的运动微分方程整理为矩阵形如下:

(24)

式中：M和C分别表示减速器系统的质量总装矩阵、阻尼总装矩阵；Km为啮合接触刚度矩阵；Kb为支撑刚度矩阵；Tout为负载矩阵；X为系统各构件的位移向量，其表达式为

3 计算结果分析

3.1 系统的动载荷

输入转速300 r/min，负载400 N·m工况下，计算得到一、二级齿轮传动啮合力动载荷时频域历程如图5、图6所示。

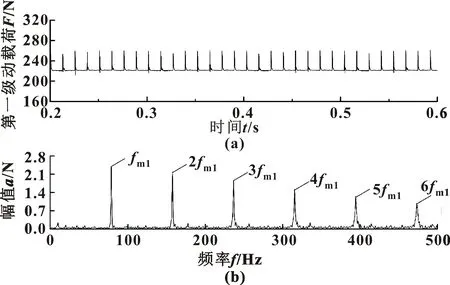
图5 一级齿轮啮合力动载荷时域(a)、频域(b)图像

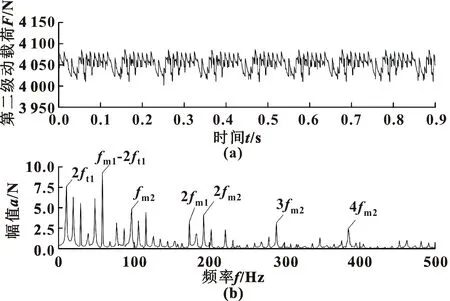
图6 二级齿轮啮合力动载荷时域(a)、频域(b)图像

由图5可看到：渐开线齿轮传动中，齿轮啮合状态单双齿交替，啮合刚度周期性变化，导致两级齿轮啮合力动载荷周期性变化。第一级动载荷的周期为0.013 0 s，均值为222.46 N；在频域历程中系统的响应以一级齿轮的啮合频率fm1及其倍频成分为主。由图6可以看出：第二级齿轮动载荷周期T为0.009 0 s，均值为4 052.66 N。由于第二级传动处于多齿啮合状态，轮齿啮合过渡过程比较平缓，动载荷较小，故在二级传动的动载荷中有一级传动的频率成分。频谱中的高频成分中以二级摆线齿轮的啮合频率fm2及其倍频成分为主。

3.2 系统的动态传动精度

文中采用动态传动误差评价各工况下减速器模型的动态传动精度。动态传动误差θerr(t)可表示为

(25)

式中:θout(t)为瞬时输出转角；θin(t)为瞬时输入转角；I为传动比。

减速器动态传动误差θerr(t)的绝对值越大，传动精度越差，反之则越好。减速器动态传动误差和输出轴转速的时频域历程如图7、图8所示。

图7 动态传动误差时域(a)、频域(b)图像

图8 输出轴转速时域(a)、频域(b)图像

由于两级齿轮的啮合刚度具有时变性，减速器动态传动误差值相应周期性变化。由图7可得：误差均值为0.654′，幅值为0.012′。在频域历程中，系统响应以一、二级齿轮的啮合频率fm1、fm2以及各自倍频成分为主。

由图8可得：减速器输出转速均值为-22.2 °/s；在频域历程中，系统响应以一、二级齿轮的啮合频率fm1和fm2以及其倍频成分为主。

从以上对减速器输出信号的时频域分析还可以看出：在计入支承和啮合弹性变形的情况下，减速器动力学模型的输出信号与理论计算一致，反映了真实减速器产品的动力学响应特性。

3.3 负载对动态传动精度的影响

为探究减速器动态传动精度与负载之间的关系，将负载作为输入变量进行求解，结果如图9所示。

图9 负载对啮合力动载荷和传动误差的影响

随着负载增加，支承和接触处弹性变形量也随之升高，导致输出转角误差呈现增长趋势。由图9可以看出：随着负载增大，减速器的一、二级齿轮动载荷幅值和动态传动误差呈现增长趋势，这一趋势与文献[17]中的实验测试结果吻合。

为探究各级传动接触及支承变形对减速器动态传动误差贡献量随负载变化的关系，定义误差贡献比率CI、CII和Cflex分别为第一级、第二级齿轮接触变形和支承弹性变形对输出转角误差的贡献比例，其中：

(26)

(27)

(28)

式中：θe1、θe2和θeflex分别为第一级齿轮接触、第二级齿轮接触和支承柔性引起的输出误差转角。各柔性因素对动态传动误差的贡献比例及输出转速幅值随负载变化关系如图10所示。可以看出：两级齿轮动载荷幅值随着负载增加，输出轴转速幅值也随负载增加而增加。可见随着负载增大，输出转速的平稳性也越来越差。在误差贡献方面，一级齿轮由于处于高速级，同时动载荷均值较小，导致第一级传动对输出转角误差贡献较小，不到5%；支承柔性因素所带来的转角误差量相对较高，占误差总量的30%左右，并且随着负载增大该比例呈现上升趋势；二级传动对输出转角误差的贡献量最大，占总误差量的60%以上，这是因为二级齿轮的动载荷均值非常大，同时二级摆线齿轮的自转与输出轴同步，导致输出转角误差对该级传动的接触弹性变形更敏感。

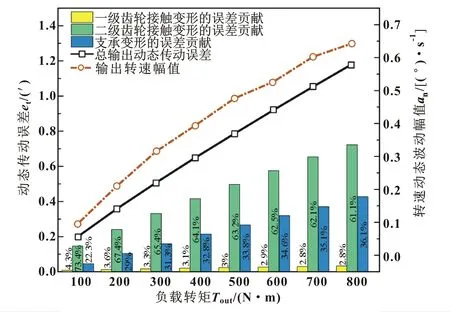
图10 负载对输出转速波动和动态传动误差成分的影响

3.4 转速对动态传动精度的影响

为探究减速器动态传动误差与转速之间的关系，将转速作为输入变量进行解算，结果如图11所示。

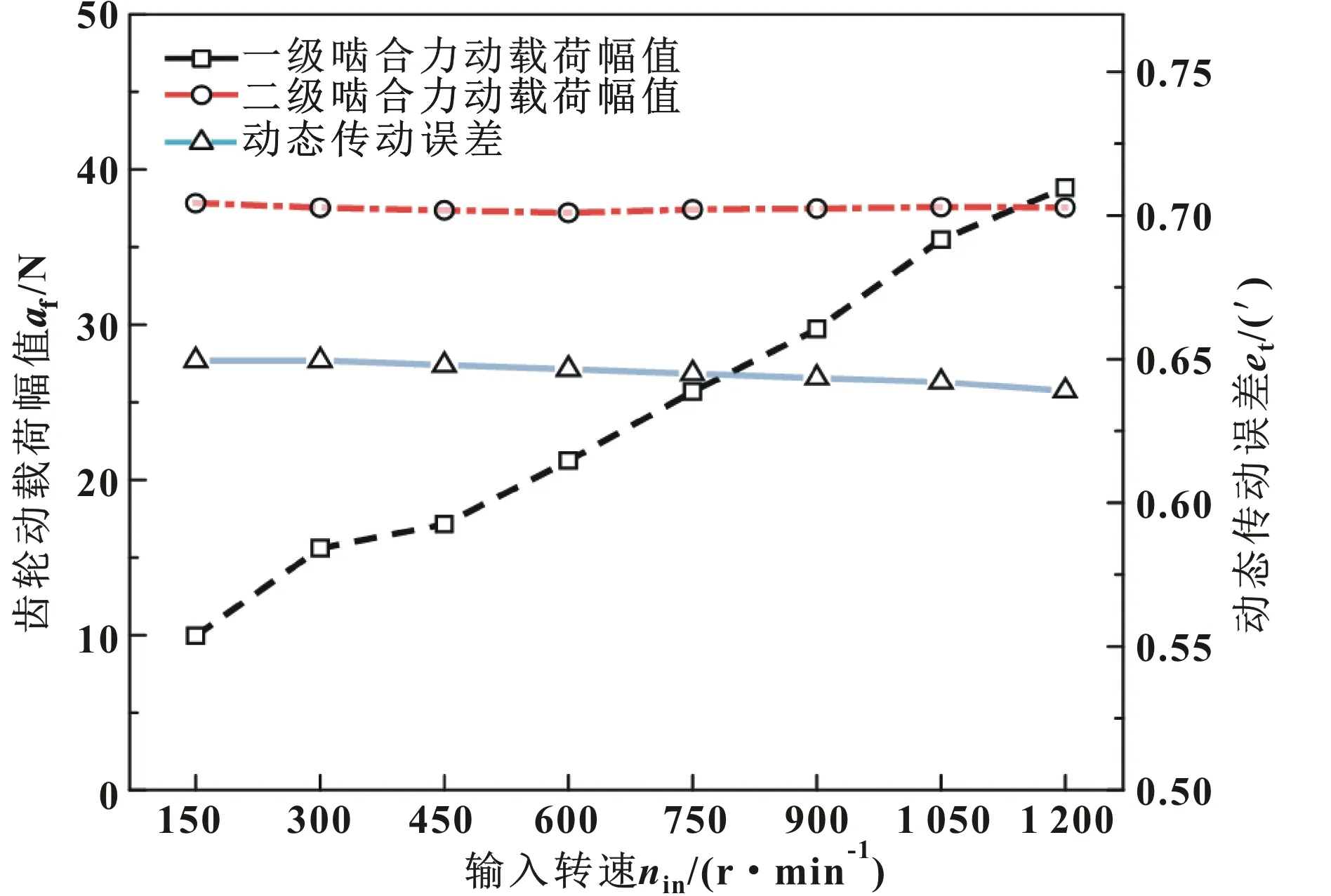
图11 转速对啮合力动载荷和传动误差的影响

从图11中可得：由于第二级摆线齿轮转动转速相对较低，且有半数轮齿同时参与啮合，啮合过程平稳，所以二级啮合力动载荷波动幅值随转速变化幅度也非常小，在38.75 N附近变化。第一级齿轮转速较高，啮合齿数少，所以齿轮传动的动载荷随转速增长的幅度比较大，传动误差始终在0.648′附近，可见输入转速对减速器传动误差影响不大，这一规律与文献[17]中的实验测试结果趋势大致相同。

图12展示了各级传动及支承柔性对动态传动误差的贡献量及输出转速幅值随输入转速变化的关系曲线。结合图11可以看出：随着输入转速的提高，一级齿轮传动动载荷幅值增大，进而导致输出轴转速幅值也随之增大。随着转速增大，减速器的传动平稳性也变差。误差贡献方面，在变转速条件下，各级齿轮啮合处及支承处的弹性变形量变化不大，一级传动的误差贡献量稳定在3%；二级传动误差贡献稳定在64%；支承柔性的误差贡献为33%左右；总传动误差稳定在0.65′处。可见输入转速对传动误差影响并不明显。

图12 输入转速对转速波动和动态传动误差成分的影响

3.5 灵敏度分析

灵敏度分析是判定模型输出信号受输入信号变化的影响程度的一种分析方法，可以用来诊断研究结果的正确性并可以预测研究结果，因此各领域常使用该方法分析研究对象。文中采用有限差分法计算BX40E减速器各处柔性因素对减速器动态传动误差影响的局部灵敏度。取Δk为系统刚度变量的一个微小变量，它对传动误差影响的灵敏度SEi计算如下式所示：

(29)

式中：ki为各柔性因素处刚度的理论值；e(ki)为柔性处刚度为ki时减速器的动态传动误差。

减速器传动精度对减速器各柔性因素的灵敏度如表2所示。

从传动误差对支承柔性灵敏度分析结果中可得：传动误差对“摆线齿轮-曲拐”支承和对“行星架-曲柄轴”支承处支承柔性灵敏度较高，敏感度值分别为0.054 2和0.036 2，传动误差对单一支承柔性处的灵敏度也在这两类支承处达到最大值，分别为0.012 1和0.018 1。表明这两处的支承柔性变化对减速器输出转角误差影响较大。因此在对减速器优化设计时，应结合轴承支承刚度Palmgren公式优先考虑提高这两类支承处的支承刚度。传动误差对太阳轮和对主轴承支承的敏感度非常小，仅为0.000 1。由于同在一级传动中，行星轮支承处的支承刚度灵敏度也很小，灵敏度值为0.000 3，这表明以上支承刚度变化对减速器输出转角误差的影响不大。

表2 动态传动误差对各柔性因素的灵敏度

在传动精度对齿轮接触刚度的灵敏性方面，由于渐开线行星轮传动和摆线齿轮传动分别位于RV减速器的第一、二级，一级齿轮轮齿变形造成的转角误差传递至输出轴时，会减小到1/i(i为减速器传动比)，所以渐开线齿轮接触刚度对传动误差的影响相较摆线齿轮传动级而言要小很多。由表2所示传动误差对接触刚度灵敏度分析可得：一、二级渐开线齿轮啮合柔性关于传动误差的灵敏度值分别为0.006 2和0.144 6。这表明第二级齿轮啮合的接触刚度对减速器输出转角误差影响较大，因此在对该类型减速器产品优化设计时，应结合Hertz接触刚度原理优先考虑提高第二级齿轮副的接触刚度。