磁流变减振器的温度场分析

马胜楠，梁冠群，周福强，危银涛

(1.北京信息科技大学现代测控技术教育部重点实验室， 北京 100192； 2.清华大学汽车安全与节能国家重点实验室， 北京 100084)

0 前言

磁流变减振器以磁流变液为阻尼介质，是一种可控的半主动阻尼器件，具有结构简单、阻尼力连续可调、能耗低、响应速度快等优点，现已广泛应用于海洋工程、桥梁结构、建筑和汽车等领域，具有十分良好的减振效果[1-6]。

在汽车行驶过程中，减振器受振动激励带动内部磁流变液的运动，由于磁流变液分子间产生摩擦导致部分机械能转化为热能，引起磁流变液温度变化。磁流变液黏度及磁导率对温度变化极其敏感，温度升高会引起输出力的下降，极端条件下甚至会引起减振器的失效[7-8]，因此对减振器温度场的分析十分必要。目前国内外的研究表明磁流变减振器在工作过程中通常受到多物理场的影响，但目前对物理场的分析多为电磁场与流固场的研究，缺乏对温度场的深入研究，导致在研究过程中出现了误差。而对温度场的分析多为在实验中设置某一固定温度测试它对阻尼力等的影响，并未考虑到阻尼器内部温度不均衡的现象，且现有技术手段无法测得阻尼器内部具体温度分布。ROSENFELD和WERELEY[9]在优化设计时仅分析了磁场的影响；NGUYEN等[10-11]综合考虑了磁场和结构参数对MR减振器性能的影响。唐龙等人[12]对磁流变液的黏温特性进行了研究，得到阻尼器在不同温度下施加不同电流时的阻尼力特性；刘旭辉等[13]通过自制阻尼器并搭建测试平台和数据采集系统，探究温度对磁流变液阻尼器输出阻尼力的影响；董小闵等[14]引入了评价系数，对较高温度下减振器是否有能力输出足够的阻尼力进行了衡量。以上研究皆未涉及到对减振器具体温度场分布情况及变化规律的研究，因此本文作者首先从理论上分析了温度对减振器阻尼力及可调系数的影响，其次对磁流变减振器进行流固传热及层流耦合建模，得到其温度场与流场的分布规律及变化情况，并通过改变冲程及参数化扫描改变阻尼间隙，得到了不同条件下温度场及流场的分布情况。研究结果为进一步分析磁流变减振器的性能提供了依据。

1 磁流变减振器结构及工作原理

图1所示为某型号磁流变减振器实物，主要由活塞杆、铁芯、线圈、缸体等组成。导线穿过活塞杆通孔为线圈供电，产生磁场，活塞杆带动活塞头做来回往复运动，磁流变液受压流经阻尼间隙，在线圈产生的磁场作用下由牛顿流体变为类固体，为减振器提供所需阻尼力。

图1 减振器Fig.1 Damper

2 温度对阻尼力的影响

磁流变减振器在实现制动、力矩传递等功能时，主要依靠的是磁流变液产生的剪切应力， 磁流变液主要由分散颗粒、基液、添加剂组成。添加剂包括分散剂和防沉剂，一般选用油酸及油酸盐、有机金属硅共聚物、脂肪醇、二氧化硅等。磁性颗粒主要应用羰基铁粉等，其工作性能受磁场强度影响，磁饱和度最大为2.1 T，而且磁导率随温度的变化也有所不同。基液是软磁性颗粒所能悬浮的连续性媒介，一般选用稳定性较好的抗磁性液体，如硅油、合成油、乙二醇等，其动力黏度受温度影响极大[15]。因此温度会通过影响磁流变液的黏度与剪切强度进而影响到减振器的阻尼力输出，因此对减振器温度场的分析很有必要。

2.1 磁流变液黏温特性

与气体不同，液体的黏度相对较大，这是因为液体分子受到它所在单元中其他分子作用力的约束，不可能在相邻两层流体间自由运动而产生动量输运。磁流变液的黏度与单元对分子的束缚力直接有关，而束缚力的强弱与分子所在势阱的深度有关，势阱深度又决定了分子在单元中的平均滞留时长t，t越小，则流动性越好，反之则越差，而流动性差的液体黏度更大。

如图2所示为实验所得某型号磁流变液黏度随温度的变化，可知：随温度的增加，磁流变液的黏度逐渐减小，从而导致输出阻尼力的降低，影响到减振器的性能。

图2 磁流变液黏温特性Fig.2 Viscous temperature characteristics of magnetorheological fluids

2.2 磁流变液磁导率温度特性

磁流变液温度变化范围一般较小，其磁导率特性可引入居里-外斯定律来描述：

(1)

式中：Xm为磁导率；C为居里常数；Tt为绝对温度；Tc为居里温度。因为无外加磁场，阻尼器产生的磁场均为线圈通电后所得，因此忽略涡流影响后，阻尼器产生的磁感应强度为

B=Xmμ0H

(2)

式中：B为阻尼间隙磁感应强度；H为磁场强度矢量；μ0为真空磁导率。得到温度对阻尼间隙磁感应强度影响关系式为

(3)

使用配制好的磁流变液进行试验，得到B-H曲线和τy-B曲线分别如图3和图4所示。由磁流变液性能曲线可用最小二乘法进行四次多项式拟合得到屈服应力与磁感应强度的关系：

τy=73.61×B4-254×B3+234.8×B2+14.44×B+0.132 2

(4)

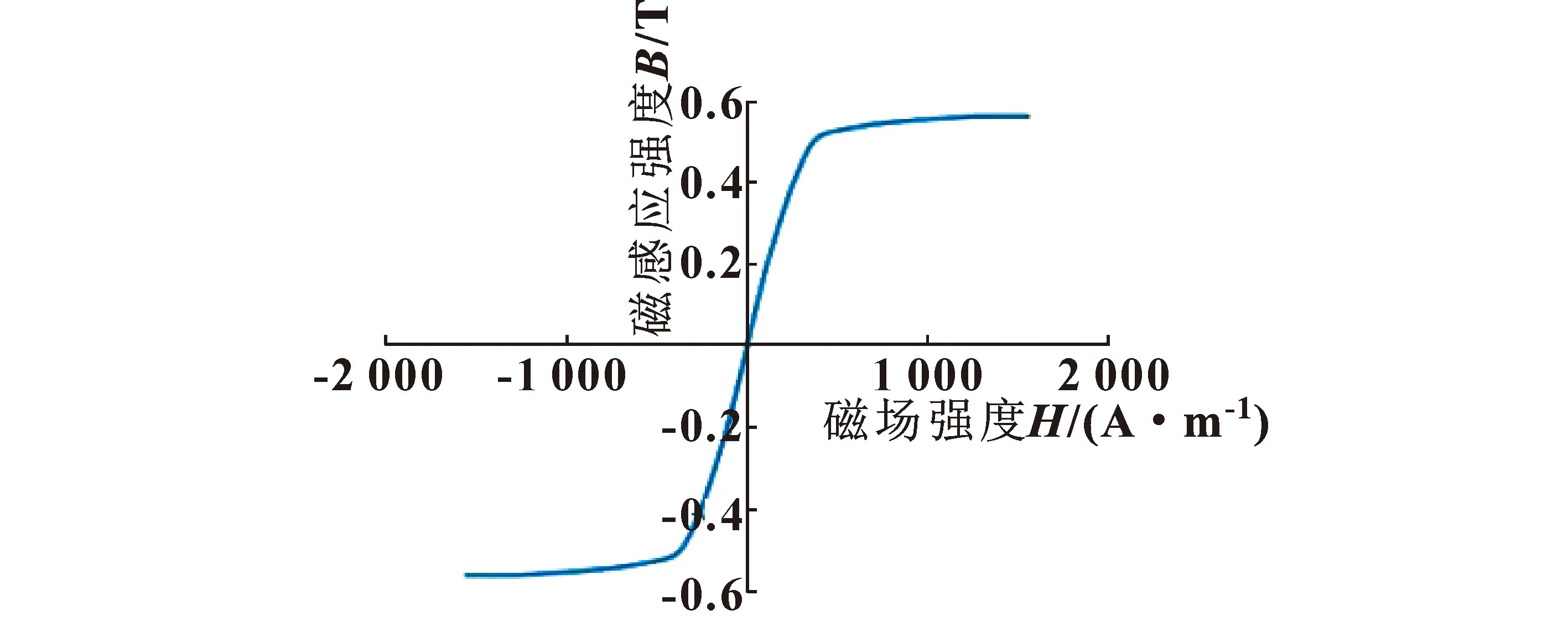
图3 B-H曲线Fig.3 B-H curve

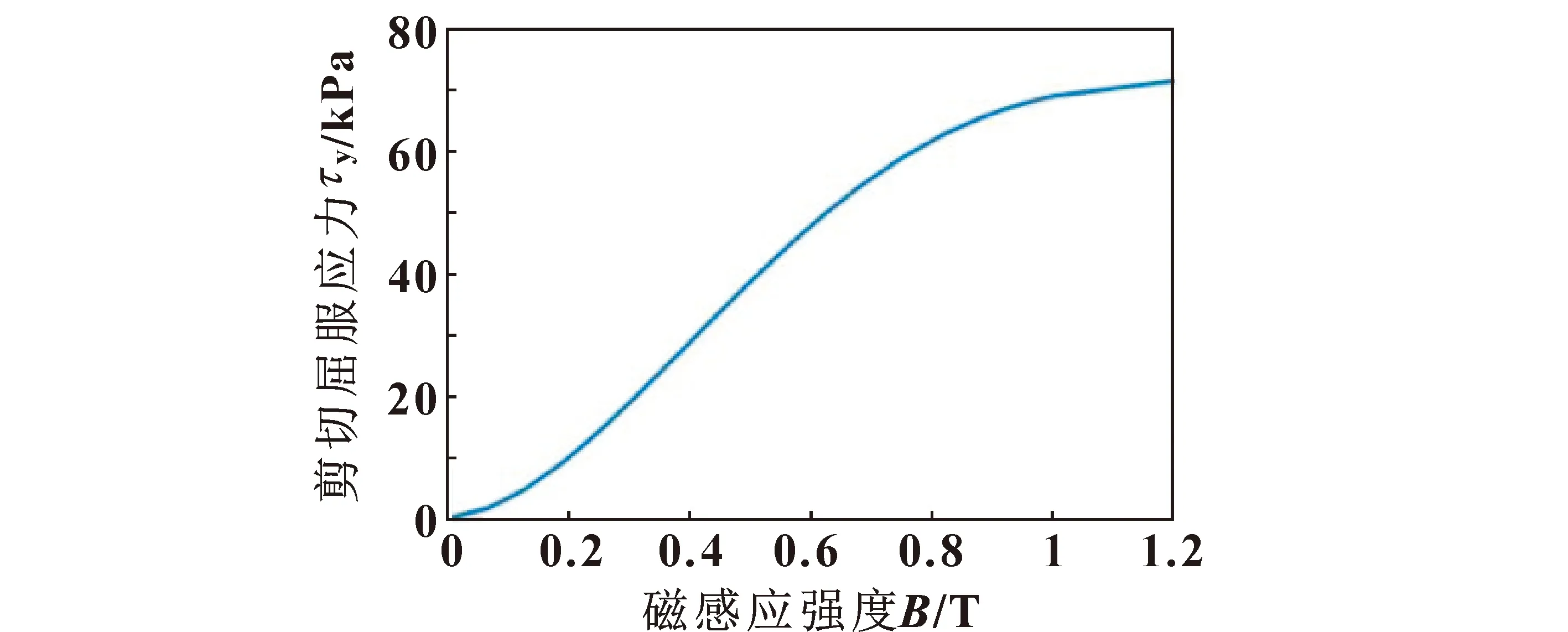
图4 τy-B曲线Fig.4 τy-B curve

综合以上分析可得，温度通过影响磁流变液的磁导率，进而影响磁场强度，最终改变剪切应力的输出值。磁导率大小与温度值成反比关系，当工作温度上升时，磁导率将会下降，进而影响到阻尼间隙内的磁感应强度。当磁感应强度值减小时，经过实验分析可得：磁流变液输出的剪切应力有所下降，直接影响到阻尼器的输出阻尼力。因此当磁流变减振器工作参数保持一致时，温升使得黏滞阻尼力与库仑阻尼力均减小。

3 温度对可调系数的影响

剪切式磁流变减振器的阻尼力力学模型为

(5)

式中：η为磁流变液的零场黏度；D为活塞头直径；L为活塞头长度；h为磁流变液间隙宽度；v为活塞与缸体的相对速度；τy为磁流变液剪切屈服应力。

磁流变阻尼器相应的动力可调系数可表示为库仑阻尼力与黏滞阻尼力之比：

(6)

当磁流变减振器工况不变时，其可调系数由剪切屈服强度及磁流变液黏度确定，实验得剪切屈服强度与黏度比值如图5所示。可知：随着温度的升高，剪切屈服强度与黏度的比值并未有明显的变化，因此可得温升对该减振器可调系数并无太大影响。

图5 温升对可调系数的影响Fig.5 Effect of temperature rise on adjustable coefficient

4 物理场数学模型

4.1 流场建模

磁流变减振器的作用机制是磁流变液的流变效应，在对减振器阻尼间隙的流场进行分析时，假设磁流变液为不可压缩流体，因此磁流变液在阻尼间隙内的流动满足纳维-斯托克斯方程：

(7)

磁流变液在阻尼间隙内的流态用雷诺数来判断：

(8)

由于阻尼间隙值一般较小，约为1～2 mm，计算得到雷诺值远小于2 320，因此磁流变液一般为层流状态。

对于稳态层流，纳维-斯托克斯方程可简化为如下形式：

(9)

磁流变液密度可以测得为3 g/cm3,假设其密度与温度无关，则流体黏度与温度的关系可以表示为

μ=μ0-α(T-T0)

(10)

式中：ρ为流体密度;u、v分别为沿x、y方向的流速；I为单位张量；T为初始温度；μ为流体黏度；μ0为初始黏度；T0为外部温度；α为热扩散率。

4.2 流固传热建模

仿真计算过程中需要对减振器缸体壁和流体域求解共轭传热，流体域中传热方式分为对流传热及传导传热2种，固体域中仅存在传导传热，且流体域与固体域之间温度场为连续的，在流体域中，黏性摩擦力引起机械能转换为热能，黏性耗散被激活：

Q+μ[∇u+(∇u)T]:∇u

(11)

其中方程右侧第二项表示黏性加热产生的热源，因此此处为全耦合的流体-热相互作用。在减振器缸体所在固体域，由于不含任何热源，因此方程可简化为

(12)

流体域与固体域之间温度场为连续的，阻尼器两端与外部相连，其温度保持恒定，根据牛顿冷却定律，减振器缸体壁的外边界热通量边界条件为

(13)

式中：Cp为恒压比热容；q为热通量；Q为热负荷；h为传热系数；Text为外部温度；A为传热面积；q0为热耗率。

5 有限元仿真

5.1 有限元建模

磁流变减振器内部的结构、温度场及流场是影响其性能的关键因素。为分析多物理场耦合作用下磁流变减振器的性能特性，根据其轴对称结构，为简化计算，在二维轴对称几何中对其建模，建立如图6所示实体模型及有限元模型。

图6 仿真模型Fig.6 Simulation models:(a)substance; (b) finite element

采用映射网格对实体模型进行网格划分，划分后形成有限元分析模型。由于仿真过程为流固传热及层流的耦合，因此网格划分需保持较高精度。为了在满足精度的要求下达到较高的计算速度，采用不同的疏密程度对它进行划分，阻尼间隙及流场边界处为主要区域，需精细划分，其他区域的网格则比较稀疏。活塞头的运动表示为振幅和频率已给定具体的谐波振荡，此运动采用任意拉格朗日-欧拉(Arbitrary Lagrangian-Eulerlian, ALE)变形网格建模，ALE方法采用动网格技术处理变形几何和移动边界的动力学，此时冲程长度为0.028 mm。

5.2 温度场仿真分析

如图7和图8所示为减振器温度场云图及温度等值线图。可知：磁流变减振器温度最高点在阻尼间隙内，从阻尼间隙到减振器两腔温度逐渐降低。由等值线分布可知，温度在阻尼间隙内分布基本一致且温度线比较稀疏，在两腔之间比较密集且形成梯度，这是由于间隙内部磁流变液流速快，温度传导快，而两腔内磁流变液流动缓慢，温度传导慢，因此形成上升梯度。

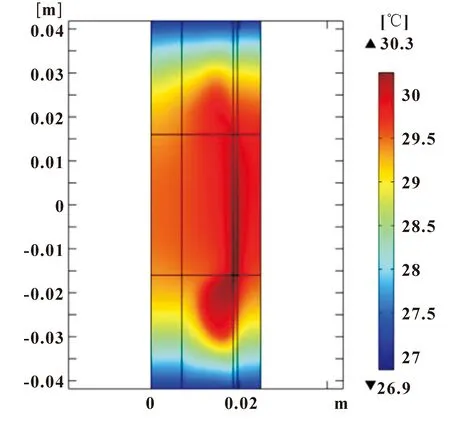
图7 温度云图Fig.7 Temperature cloud map

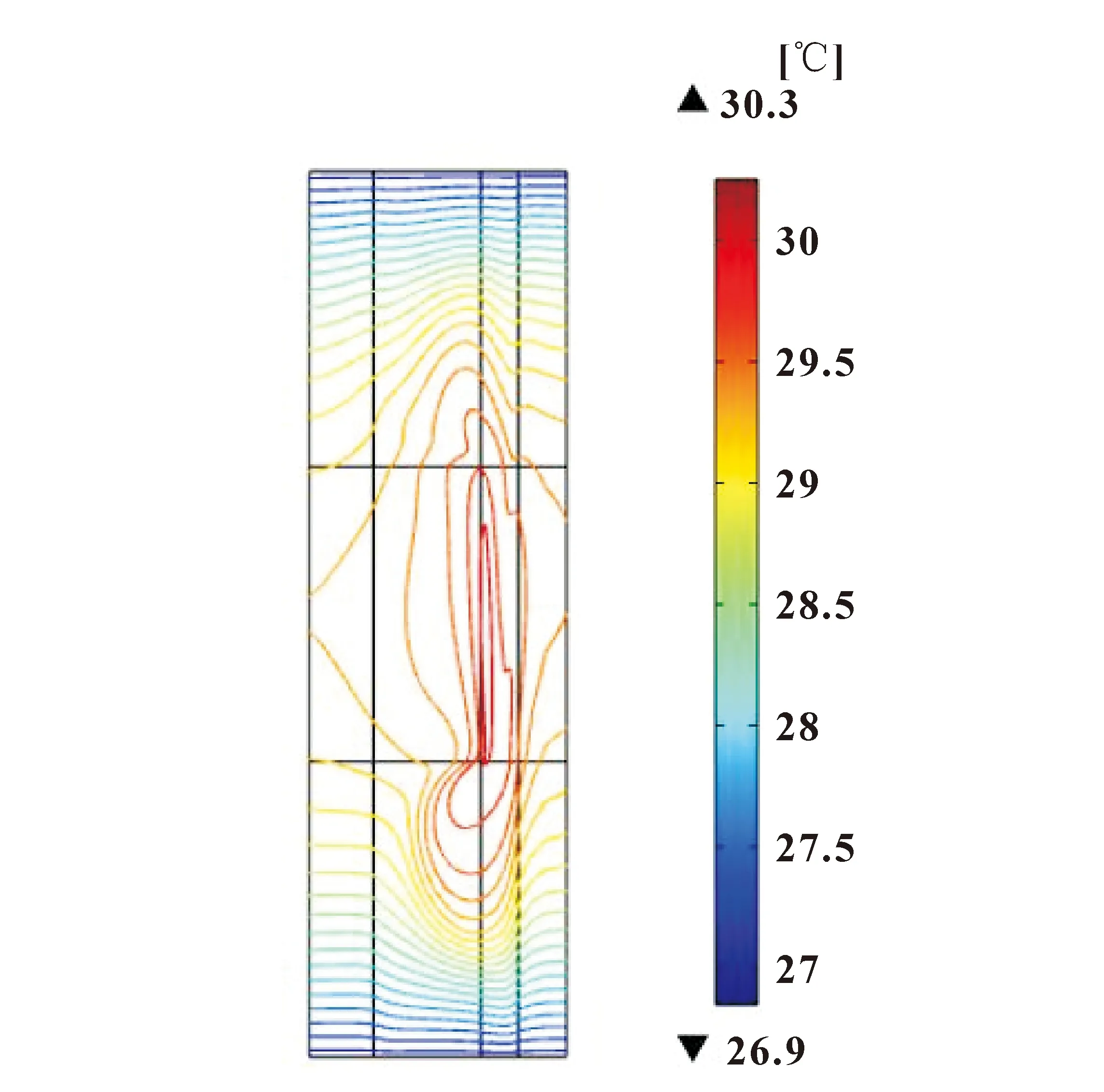
图8 温度等值线Fig.8 Temperature contour line

如图9所示为3个域点处的温度随时间的变化，图10所示为冲程结束后沿阻尼器内壁的温度分布。由图9可知：阻尼器在运行过程中，其冲程结束位置的温度是呈波浪形上升状态，但冲程结束位置并非阻尼器的最高温度。由图10可知：在运行几个周期以后，最高温度为30.15 ℃，最低温度为26.9 ℃，阻尼器中心附近的温度仅上升了约3.25 ℃，即最高温度上升幅度约为10.8%。

图9 域点温度随时间变化Fig.9 Domain point temperature changes with time

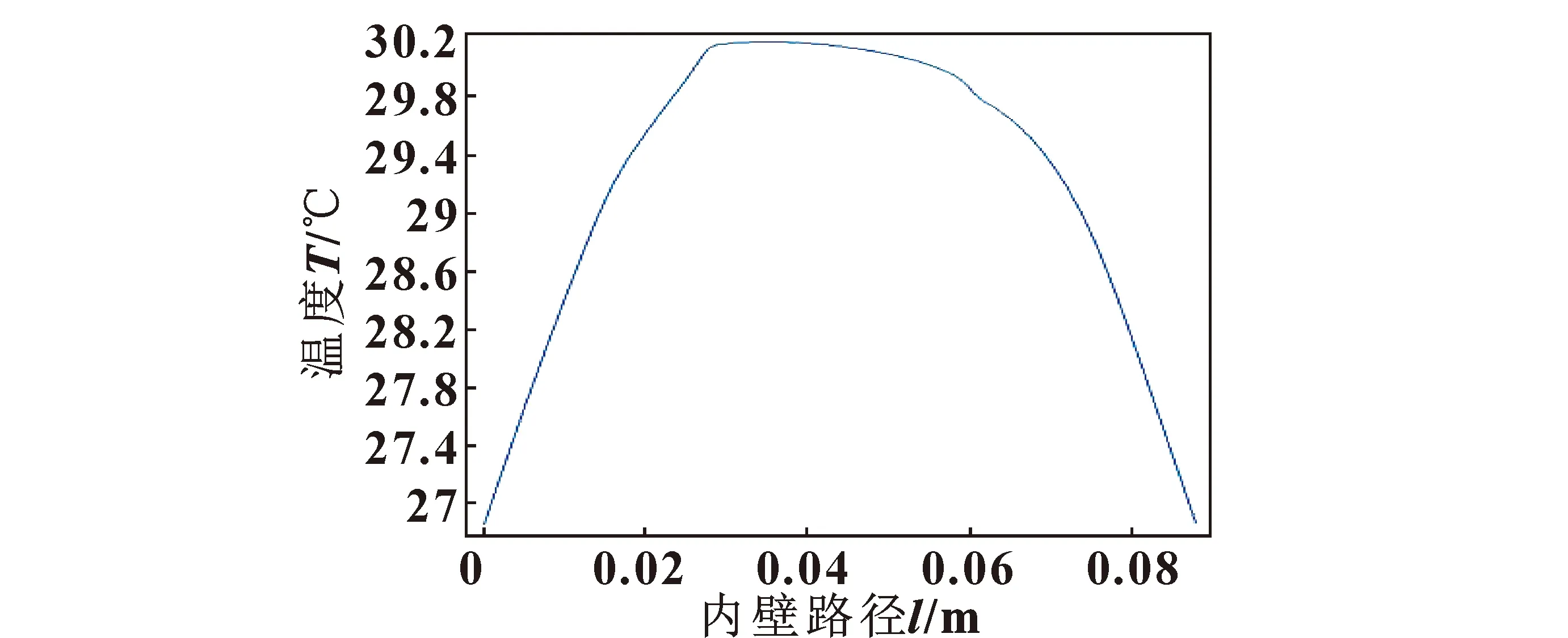
图10 沿内壁温度Fig.10 Temperature along the inner wall

5.3 流场仿真分析

流场仿真中，考虑温度对磁流变液黏温特性的影响，忽略磁场对其流变效应的影响，在减振器两端及缸体内壁上设置壁边界条件为无滑移，而对活塞头边界及活塞杆设置壁边界条件为移动壁/滑移壁。将流体设置为黏度受温度影响的非牛顿流体，分析磁流变减振器运动过程中的流场速度、压力等的分布。

给定活塞头运动方程为x=Asin(2πft)，设置振幅A=0.012 m，频率f=0.4 Hz，磁流变减振器做往复运动时内部的流线分布如图11所示。阻尼间隙内流线均匀规律且比较密集，说明内部流速较大，阻尼间隙两端流线稀疏且分布不均，说明该区域内流速慢且流况复杂。

图11 流线Fig.11 Streamline

由图12可知：两腔内流速较小，阻尼间隙内流速较大。这是因为阻尼间隙处，液体流经横截面积发生突变，通流面积减小，导致流速瞬间增加，阻尼间隙出入口处速度变化极其剧烈，由云图可知，速度呈火焰状分布。

图12 流速云图Fig.12 Flow velocity cloud map

定义压力点约束如图13所示，即此处压力为0，得到最后时刻压力分布。可知：磁流变减振器两腔之间存在较大压力差，磁流变液受压产生流动，流经阻尼间隙。阻尼间隙内部产生较大压降，而两腔各自内部则压力基本一致，这是因为两腔内磁流变液流速低，因此压力变化不明显，压力分布较均匀。

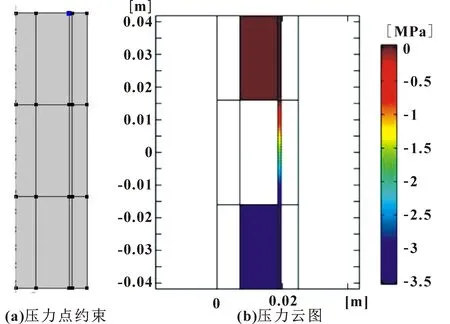
图13 压力分布

由图14可知：在无磁场状态下，由于温度的影响，磁流变液的动力黏度在阻尼通道附近最小，反而在两端较大，因此可知温升会降低磁流变液的动力黏度，进而减小屈服应力。

图14 动力黏度分布Fig.14 Dynamic viscosity distribution

已知磁场通过磁流变效应使得剪切屈服强度增加，但温度通过对磁导率等的影响会使得磁流变效应减弱，因此可知温度会通过改变磁导率来减弱磁场的作用，但减弱程度与磁流变液配方等有关，需具体情况具体分析，因此此处仅讨论了无磁场时的温度场情况。

5.4 条件改变对热流场的影响

5.4.1 改变阻尼间隙

使用参数化扫描，改变阻尼间隙值，分别取1、1.2、1.4、1.6、1.8 mm，计算后得到如图15所示不同阻尼间隙的内壁温度值和如图16所示不同阻尼间隙对应的速度云图。

图15 不同间隙的内壁温度Fig.15 Inner wall temperature with different gaps

图16 不同阻尼间隙对应的速度云图Fig.16 Velocity clouds map of different damping gaps: (a)1 mm; (b)1.2 mm; (c) 1.4 mm; (d)1.6 mm; (e)1.8 mm

由图15可知：当阻尼间隙增加以后，磁流变阻尼器的内壁温度差减小，温度值也减小，且在1～1.4 mm之间温度变化较大，约为2.9 ℃，在1.4～1.8 mm之间温度值的减小量较小，在0.3 ℃左右。阻尼间隙在1～1.8 mm，温度最大值的变化幅度为10.8%。

由图16可知:随着阻尼间隙的增加，间隙内磁流变液的速度梯度变小，流通速度也随之减小，喷射流区域增大，且在1.2～1.4 mm之间，速度的变化值较大，约为0.15 m/s，而在1～1.2 mm及在1.4～1.6 mm之间，速度的变化值约为0.05 m/s，在1.6～1.8 mm之间，速度值变化最小，约为0.02 m/s。阻尼间隙在1～1.8 mm，流速最大值的变化幅度约为77%。

5.4.2 改变冲程长度

为了更好地探究阻尼器的温度场与流场变化，将阻尼器冲程加长为0.056 mm，计算后得到如图17所示长冲程下3个域点处的温度随时间的变化，图18所示为阻尼器内壁的温度分布。

由图17与图18可知：阻尼器冲程结束后，温度升高约18 ℃，比起短冲程阻尼器，长冲程的温升更加明显，因此在长冲程阻尼器中温度的影响必须考虑。由于阻尼力由库仑阻尼力与黏滞阻尼力组成，库仑阻尼力受温度的影响较小，黏滞阻尼力受温度影响较大，因此随着温度上升，黏滞阻尼力有所增加但库仑阻尼力增加较小，因此可通过增加库仑阻尼力、提升库仑阻尼力的占比来提高阻尼器的力学性能温度稳定性。

图17 3个域点处温度随时间变化Fig.17 Temperature at three domain points varies with time

图18 内壁温度Fig.18 Inner wall temperature

6 结论

通过理论分析、层流及流固传热数学模型推导、多物理场耦合仿真，研究了磁流变减振器的温度场及流场特性，得到结论如下：

(1)由实验验证磁流变液黏温特性，得知其黏度随温度降低；引入居里-外斯定律得到磁流变液磁导率的温度特性，得知温升引起磁导率下降。因此得到当阻尼间隙内发生温升时，由于黏度及磁导率的下降，阻尼力输出减小。

(2)减振器运行过程中，阻尼间隙内的温度不断上升，最高温度出现在阻尼间隙内部而不是冲程结束处。阻尼间隙内温度分布比较均衡，温度梯度出现在间隙外。阻尼器中心附近的温度仅上升了约3.2 ℃，即最高温度上升幅度约为10.8%。流场中，速度在阻尼间隙出入口处发生突变，呈火焰状分布，压力梯度出现在阻尼间隙内部，外部无明显压力差，动力黏度在阻尼间隙处最低。

(3)阻尼间隙增加，温度值减小，且减小量逐渐降低，从1 mm到1.8 mm，温度最大值降低幅度为10.8%。流速最大值的变化幅度约为77%，且从1.2 mm到1.4 mm之间，速度的变化值最大。增加冲程长度为0.058 mm后，温升更加明显，阻尼器中心附近的温度升高约18 ℃，可通过增大库仑阻尼力来增加库仑阻尼力在整体阻尼力中的占比，进而提升阻尼器的力学性能温度稳定性。

已知磁场产生的磁流变效应使得阻尼间隙内产生剪切屈服，但经上述研究可知，温升通过改变磁导率可削弱磁场的作用。但削弱程度因磁流变液的配方等而有所不同，因此温度场的研究确实必要。下一步应耦合考虑磁场及温度场的双重影响，针对某一配方的磁流变液深入探讨温度场对磁场的削弱作用，继续进行深入研究。