例谈直观想象素养发展下的解析几何问题的拓展

2023-02-03金东平

中学教研(数学) 2023年1期

金东平

(萧山中学，浙江杭州 311201)

在实际教学中，只有少数学生能将解析几何大题做到底，大多数学生会出现“有点思路”“运算好烦”“算不到底”的现象.为什么会出现这种现象？从解题过程中笔者发现学生对图形的整体认识不够全面，图形与图形、图形与数量的关系把握不到位，因此在解题教学中有必要培养学生的直观想象素养.

直观想象是指借助几何直观与空间想象感知事物的形态与变化，利用空间形式特别是图形理解和解决数学问题的素养.主要包括：借助空间形式认识事物的位置关系、形态变化与运动规律；利用图形描述、分析数学问题；建立形数的联系，构建数学问题的直观模型，探索解决问题的思路.本文以直观想象素养为着手点，结合具体实例，对解析几何的教学谈一点点建议.

1 问题呈现

例1如图1，已知⊙C的方程为x2+(y+1)2=r2(其中r>0)，过点N(-1,1)作两条直线分别交抛物线y=x2于点P，Q，并且都与动圆相切，求证：直线PQ经过定点，并求出定点的坐标.

从知识点上看，本题主要考查直线与直线、直线与圆、直线与抛物线的位置关系.从能力上看，主要考查学生能否利用图形的描述分析对应的数学问题，并建立图形与代数表达式的联系，然后借助代数表达式的特点构建直观模型，探索解决问题的思路.

2 解法探究

2.1 借助图形的动态变化发现规律

从图形的动态变化看：圆的半径发生变化导致直线NQ,NP的位置发生改变.在这个变化过程中会有什么规律？直线NP，NQ的斜率k1，k2会有怎样的数量关系？

2.2 描述图形的位置关系和度量关系

用数学的语言描述“过点N(-1,1)作两条直线分别交抛物线y=x2于点P，Q，并且都与动圆C相切”如下：

设直线NP，NQ的斜率分别为k1，k2，则直线NP的方程为

y-1=k1(x+1)，

即

k1x-y+k1+1=0,

同理得直线NQ的方程为

k2x-y+k2+1=0.

由NP，NQ与动圆C相切的位置关系得到k1，k2的数量关系

化简得 (k1-k2)[4k1k2+3(k1+k2)-4]=0.

因为k1≠k2，所以

4k1k2+3(k1+k2)-4=0.

2.3 建立图形与图形关系

解题的目标是“求证直线PQ经过定点，并求出定点的坐标”，需要关注点P，Q的位置.

从图形与图形的关系看：点P，Q不仅在抛物线y=x2上，也在直线PQ上.利用这一关系，探索解决问题的思路有3个角度：

1)点P是抛物线y=x2与直线PN的交点，点Q是抛物线y=x2与直线QN的交点；

2)点P是直线PQ与直线PN的交点，点Q是直线QP与直线QN的交点；

3)点P是直线PQ与抛物线y=x2的交点，点Q是直线QP与抛物线y=x2的交点.

分析1回归例1，根据点P是抛物线y=x2与直线PN的交点，点Q是成抛物线y=x2与直线QN的交点，求出点P，Q的坐标，借助直线PQ的方程，探究直线PQ是否经过定点.

解法1设直线PN的方程为

y=k1(x+1)+1,

将直线PN与抛物线联立，得到方程组

消去y,得

x2-k1x-(k1+1)=0,

解得x1=k1+1，从而点P的坐标为(k1+1,(k1+1)2).同理可得点Q的坐标为(k2+1,(k2+1)2)，从而

kPQ=k1+k2+2，

于是直线PQ的方程为

y-(k1+1)2=(k1+k2+2)[x-(k1+1)]，

分析2直接求直线PQ的方程有困难，但是借助点P，Q在直线y=kx+m上的几何关系建立k,m的数量关系，可探究直线PQ是否经过定点.

解法2设直线PQ的方程为

y=kx+m,

点P(k1+1,(k1+1)2)，Q(k2+1,(k2+1)2)在直线y=kx+m上，得

(k1+1)2=k(k1+1)+m,

(k2+1)2=k(k2+1)+m,

从而k1,k2是方程(x+1)2=k(x+1)+m的两个根,即k1,k2是方程x2+(2-k)x+1-k-m=0的两个根，由韦达定理,得

k1+k2=k-2, k1k2=1-k-m.

因为4k1k2+3(k1+k2)-4=0，所以

4(1-k-m)+3(k-2)-4=0,

即

k+4m=-6，

分析3根据点P是直线PQ与直线PN的交点，点Q是直线QP与直线QN的交点，求出点P，Q的坐标.借助点P，Q在抛物线y=x2上的几何关系建立数量关系，探究直线PQ是否经过定点.

解法3设直线PQ的方程为

y=kx+m，

直线NP，NQ的斜率分别为k1，k2，则直线NP的方程为

y-1=k1(x+1)，

即

k1x-y+k1+1=0,

同理得直线NQ的方程为

k1x-y+k2+1=0.

联立直线NP与直线PQ，得到方程组

又因为点P,Q都在抛物线y=x2上，满足方程

所以k1,k2是方程

的两个根.进一步可知k1,k2是方程x2+(2-k)x+1-k-m=0的两个根，由韦达定理得

k1+k2=k-2, k1k2=1-k-m.

因为4k1k2+3(k1+k2)-4=0，所以

4(1-k-m)+3(k-2)-4=0,

即

k+4m=-6，

分析4根据点P是直线PQ与抛物线y=x2的交点，点Q是直线QP与抛物线y=x2的交点，找到x1,x2,k,m的数量关系.借助直线NQ,NP的斜率k1,k2的关系，探究直线PQ是否经过定点.

解法4设P(x1,y1)，Q(x2,y2),直线PQ的方程为

y=kx+m.

将直线PQ与抛物线方程联立，得到方程组

化简得

x2-kx-m=0.

由韦达定理得

x1+x2=k, x1x2=-m，

因为

所以

k1+k2=x1+x2-2=k-2,

k1k2=(x1-1)(x2-1)=x1x2-(x1+x2)+1

=-m-k+1.

又因为4k1k2+3(k1+k2)-4=0，可得

评注4种不同的解题方法有其共同的特点：借助图形的动态变化发现规律，描述图形的位置关系和度量关系，建立图形与图形、图形与数量的关系，探索解决问题.教师在教学中应引导学生整体把握图形的特点，找准关键的信息，合理转化代数形式，探索解决问题的思路.

3 解题反思

思考14k1k2+3(k1+k2)-4=0的数量关系蕴涵的几何图形有什么特点？

在上述的4种解法中我们始终围绕k1,k2的数量关系4k1k2+3(k1+k2)-4=0，这个表达式是我们解决问题的核心，它背后蕴涵的几何特征是什么？

k1=tanα, k2=tanβ,

且

4k1k2+3(k1+k2)-4=0,

于是

故4k1k2+3(k1+k2)-4=0的几何特征是α+β为定值.

思考2直线PQ经过定点的充分条件是什么？

从图形的特征中寻找到“直线PQ经过定点”的充分条件是“α+β为定值”.

依据例1的证法2，还可以探寻到如下3个“直线PQ经过定点”的充分条件.

设直线NP，NQ的斜率分别为k1，k2，则直线NP的方程为

y-1=k1(x+1)，

即

k1x-y+k1+1=0，

同理得直线NQ的方程为

k2x-y+k2+1=0.

又因为点P,Q都在抛物线y=x2上，所以

故

思考4将抛物线y=x2改为椭圆或者双曲线是否有这样的结论呢？

设直线AP，AQ的斜率分别为k1，k2，则直线AP的方程为

y=k1(x-2)+1，

同理得直线AQ的方程为

y=k2(x-2)+1.

又直线PQ的方程为

y=kx+m，

于是

又因为2k1k2+k1+k2-2=0，所以

-(m-1-2k)+2(k+1)-2(1+2k+m)=0,

即

3m-1=0，

1)求l的斜率；

(2022年全国数学新高考Ⅰ卷第21题)

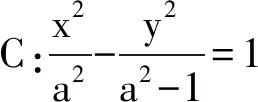
1)由变式5的解答过程可知

由直线AP,AQ的斜率之和为0，即k1+k2=0，解得k=-1.

由变式5的解答过程可知

点A到直线PQ的距离为

点P的横坐标为

点Q的横坐标为

评注对几何图形的观察，抓住图形的关键特点，并抽象出它背后的数量关系.对代数表达式的观察，需要分析隐含的几何模型，这些都是数学的抽象过程，也是思维深刻性的具体表现.建立图形和代数的关系，解决问题的方向就会呈现多样性，“如何选择方法、如何选择最优”是思维灵活性的体现；同时可建立图形与图形的联系，推广到其他的问题，这是思维的发散性的体现.这些思考对学生提升直观想象素养有很大的帮助.

4 教学启示

直观想象是发现和提出数学问题、分析和解决问题的重要手段，是探索和形成论证思路、进行逻辑推理、构建抽象结构的思维基础.直观想象主要表现为：建立形与数的联系，利用几何图形描述问题，借助几何直观理解问题.

4.1 重视数学表征

数学表征是指某种形式表达数学概念或关系的过程.学生要理解某个数学问题，就必须在这个数学问题与一个更容易理解的数学问题之间建立一个映射，而表征就是这个映射过程.在教学中，教师要多鼓励学生用图形语言、数学语言从不同的角度描述要处理的数学概念或关系.

4.2 重视对数学本质的感悟

数学的本质简单、自然，它们的根源往往蕴涵着几何直观.如4k1k2+3(k1+k2)-4=0中蕴涵着两条直线倾斜角的和是定值.在解题过程中，如果没有思路，那么我们可以引导学生从目标出发，利用结构代数式的几何特征和几何关系，进而解决问题.无论是将形的问题转化为数的问题还是将数的问题转化为形的问题，都需要学生具备较好的直观想象能力.