探索本质 深挖根源
——导数试题命制中的点滴思考
2023-02-03叶事一包日可
叶事一, 包日可
(1.温州市教育教学研究院,浙江 温州 325000;2.平阳中学,浙江 平阳 325400)
通过给某一知识点制定一道试题,测验考查学生对知识的掌握情况以及对解题方法的运用能力就是命题.学生的解题方向,通常可以从试题命制的背景寻找突破口,因此,准确把握命题是考查学生对知识的掌握情况的重要方面,而命题又并非只是知识点表层的考查,更重要的是考查学生的解题能力[1].如何准确把控所命制的试题,需要从知识背景出发,从考查能力入手,抓住运用数学思想方法解题的本质.于是,在命题的过程中,我们往往需要将知识点呈现出来,将思想方法隐藏起来,而学生在解决问题时往往又需要将其层层剖析,运用转化与化归思维,寻找解题的突破口.
1 命题背后的隐藏——“意”味“深”长
高考试卷中的导数题,其本质在于运用导数工具研究函数的性质,以研究零点为载体,综合不等式、含多个参变量等因素,其诸多解法都犹如“水中月,镜中花”,让人可望不可及,如“放缩取点”“端点效应”“凹凸反转”“指对同构”等,可见其深度.探索发现,此问题“深”在于零点中的隐零点,在于参数中的隐参数,在于不等式的“放”与“缩”,在于变量中的“多变”.而如何将“深”不可测的问题进入我们的可测范围,需要恰当运用数学解题思想方法,研究各个“深”处的难点,方能寻得突破口.
笔者以2021年浙江省数学高考的导数题为例,通过分析试题的背景谈解题.

(2021年浙江省数学高考试题第22题)
分析首先对试题中的函数进行深入分析,通过导数工具了解其单调性,存在唯一极值点x0=lnb,分析所证的问题,其难点在于多变量的处理.不难发现变量间的关系以及零点所在的范围,可知
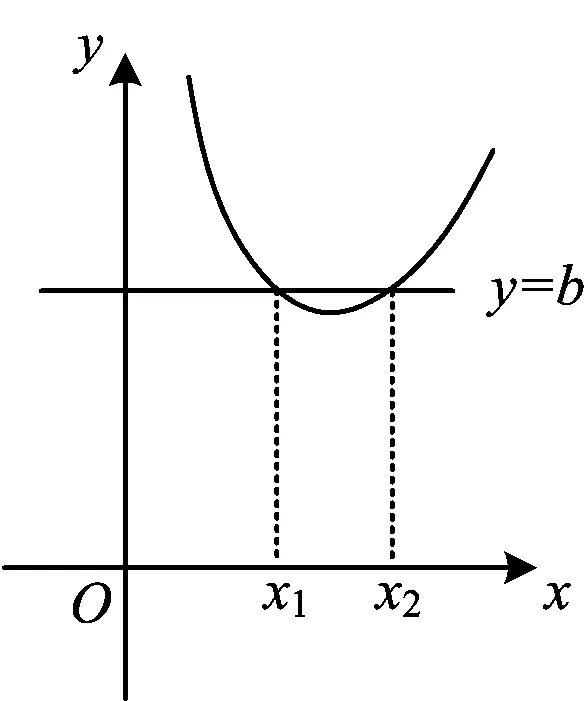
0 从而 bx1=ex1+e2<2e2. 欲证 从解题的角度命制试题,体现多思维、多推理,少些套路.导数问题的命制通常是多元、隐零点、隐参数、恒成立、不等式集一身的综合问题.而解决这些问题的策略在于运用数学思想方法,如主元思想、消元思想、构造函数、同构思想、放缩思想等,特别是多变量问题中,消元思想尤为关键,常见的有关系代入消元、嵌套函数消元、放缩消元等.从多角度、多方法看待导数问题,与不等问题的放缩结合,可进可退,进可攻,退可守,颇有威力.下面以例2为例,谈命制的试题中解题方法的“深”入“浅”出. 图1 (2021年浙江省数学高考试题第22题改编) 思路1嵌套原函数消元. 如图1,分析可知x2>lnb,且y=f(x)在(lnb,+∞)上单调递增,于是可以嵌套原函数进行消元,则原命题即证 即证 即 两边取对数,得e2 思路2嵌套构造的函数消元. 图2 令ex-bx+e2=0,得 即 以下同上(略). 思路3放缩消元. 分析可知x2>lnb>e,由ex2-bx2+e2=0,得 评注由于x2与b的关系为ex2-bx2+e2=0,无法通过其关系直接替代消元,于是通过嵌套原函数消去零点x2,也可以通过嵌套分离后构造的函数,利用φ(x2)=b进行消x2,二者的前提都需要满足不等式中的左右两个式子在嵌套的函数的单调区间内,因此,命题者刻意地限制b>e4,并容易找到相应的嵌套函数.同时,由于范围的许可,思路3有了依据,而常常在范围许可之内,不等式的证明问题往往可以通过放缩进行消元. 这样的多角度消元,在命题过程中设置较为困难,往往会将范围放宽,便于寻找合适的函数嵌套,或者做适当的放缩消元.这样,多元问题的消元方可进退有“度”. 许多试题善于对知识进行隐藏,而就是这样的深度隐藏,造就了解题思维的深度.深挖其命题隐藏的奥秘,运用数学的转化思想,使之呈现出原来的面貌,方可喜出望外.下面以命制一道导数的试题经历为例,谈命题中的深“藏”不“露”. 首先确定一单参函数 易知 图3 如图3,当0 通过几何画板工具,发现参变量a与零点x1,x2间存在着等与不等的关系,即g(x1)=g(x2)=a,且有a>x1,ax2>1等. 要证a>x1,只需证g(a)>0.而 所以 若从拆分转化的方法角度做问题的隐藏,则可将“a>x1”与“ax2>1”两个性质做整合,隐藏在一个不等式中,如做同向乘法运算,可提出问题“a2x2>x1”,欲证“a2x2>x1”,只需将其拆分为证明“a>x1”与“ax2>1”即可.类似做同向加法运算,也可以提出问题“a(x2+1)>x1+1”,证明类似. 变式2证明:a2x2>x1. 变式3证明:a(x2+1)>x1+1. 钩“深”索“隐”,即钻研深处,探索本质.函数的基本性质有有界性、单调性、奇偶性、周期性以及凹凸性等,其中,单调性可以由一阶导数工具来研究,凹凸性可以由二阶导数来研究,而用导数研究某一函数过于直接.在命制试题中,是否可以将函数的性质显露出来,又不好用导数工具解题,即可以将导数工具的方法隐藏起来呢?以下以一个函数的凹凸性研究为例谈如何究其函数本质特征,钩深索隐. 2)设I是(0,+∞)上的一个子区间,f(x)是I上取值非负的函数.任取x1,x2∈I,若恒有 则称函数f(x)为I上的几何凹函数;若恒有 则称函数f(x)为I上的几何凸函数. ≥-a(t2lnt1+t1lnt2)+lnt1lnt2. 另一方面, 证毕. 函数的凹凸性与其几何凹凸性的区别在于:二者不能互推,它们互为既不充分也不必要条件,但又有一定的关系.在上述特例下,由于y=f(x)在[e,+∞)上单调递增,又 于是 同时y=f(x)在[e,+∞)上为凸函数,故 于是有如下命题成立: 同时,若增添条件,则二者又有如下命题成立: 设正值函数f(x)定义在I(其中I⊆R+)上,若对任意的x1,x2∈R,有 且 则恒有 即证 不妨设g(x)=lnf(ex),其中x∈I,等价于证 即证y=g(x)在x∈I上为凹函数. 因此,对一个具备几何凸性的函数,只需构造函数 g(x)=lnf(ex),其中x∈I, 其几何凸性与y=g(x)的函数凹性等价. 于是,对上述特例的解析如下:不妨设 g(x)=lnf(ex)=ln(aex-x),其中x∈[2,+∞), 下证y=g(x)在x≥2上为凹函数. 得证. 函数零点间的多变量不等关系,在于寻找关系与不等关系,在于消元与函数的嵌套,在于放缩与曲直拟合,在于对函数性质本质的把握.能紧扣函数性质的本质,立足其“根本”,多角度、全方位挖掘其中的内涵,必能达到“枝繁叶茂”的成效. 数学之美在于其简洁与严谨.以上试题便体现了数学之美,美在数学式子的简洁,美在解题的严谨思维,美在命题者的构造精妙,美在其深“藏”不“露”[2].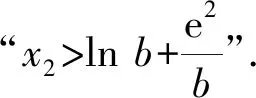
2 命题解题的方法——“深”入“浅”出

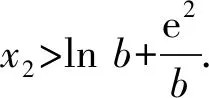


3 命题思想的挖掘——深“藏”不“露”
3.1 选研究对象

3.2 寻研究性质
3.3 证研究性质
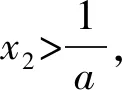
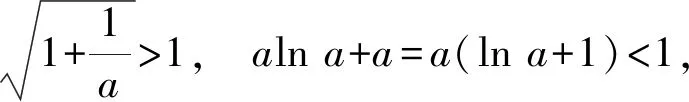
3.4 藏研究过程

3.5 定研究试题


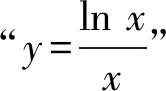
4 命题本质的探索——钩“深”索“隐”
4.1 定义性质

4.2 发现性质
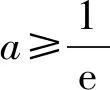
4.3 证明性质
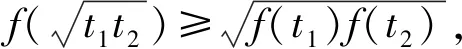
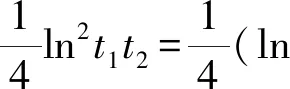

4.4 区别联系
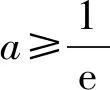
3.5 钩“深”索“隐”

5 命题探究的反思
