构造轨迹求最值 点线距离巧迁移
——2022年嘉兴南湖区数学中考一模第16题赏析
2023-02-03易良斌
王 勤, 易良斌
(1.绿城育华嘉兴长水实验学校,浙江 嘉兴 314000;2.浙江省易良斌名师工作室,浙江 杭州 310020)
《义务教育数学课程标准(2022年版)》(以下简称《新课标》)对于图形与几何要求“从演绎证明、运动变化、量化分析3个方面研究图形的基本性质和相互关系”[1].近几年中考数学试卷填空压轴题中关于求线段最值的问题,因其既具备运动变化特征又能考查学生解决问题过程中的演绎证明、量化分析能力而倍受命题者青睐.现以2022年浙江省嘉兴市南湖区中考数学一模试题第16题为例,对解题思路进行结构化分析,以期形成解决该类型试题的通性通法,使之易被理解,并运用于类似问题的解决中.
1 原题呈现

图1
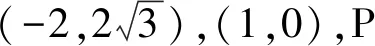
(2022年浙江省嘉兴市南湖区中考数学一模试题第16题)
此题满分为4分,学生平均得分1.80分,难度系数0.45.第一空相对容易,难度系数0.76,第二空动点问题有区分度,是对学生综合解题能力的考查.该题涉及平面直角坐标系中几何图形、直角三角形斜边上的中点等知识,结构简洁,立足教材,关注基础,内涵丰富,重视理解与应用,体现了数学核心知识、运算与推理素养.试题以平面直角坐标系中动直角三角形斜边上的中点为主要载体,探寻解法的过程中还会融入圆、图形变换等知识.线段BM的两个端点一定一动,寻找动点M的运动规律,也即在变化中寻不变、在不变中找关系,是解决问题的关键.

图2
2 思路探究
2.1 基本图形
由已知点M是线段PQ的中点,可联想到斜中线定理,即“直角三角形斜边上的中线等于斜边一半”,形成思路1.
思路1如图2,联结AM,OM,由AM与OM分别是Rt△APQ与Rt△OPQ斜边上的中线,得
由此可知点M必在OA的中垂线上,即点M的运动轨迹是OA的中垂线,从而BM的最小值就是点B到AO中垂线MN的垂线段BH的长.由∠AOQ=30°,得
从而N(-4,0),于是
2.2 一中同长
由△QAP是直角三角形、点M是斜边PQ上的中点,可联想Rt△APQ内接于圆,且以点M为圆心,可形成思路2.
思路2如图3,由△QAP,△QOP都是直角三角形可得点Q,A,O,P共圆.据此由⊙M中半径相等,得
则点M的轨迹是AO的中垂线MN,下同思路1.
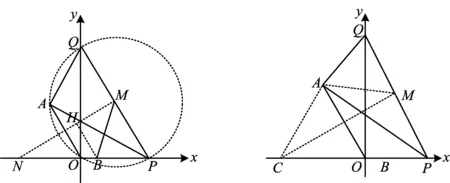
图3 图4
2.3 旋转相似
构造相似形,也是找出点M所在轨迹的常用方法.
∠APQ=∠AOQ=30°.
易得△AQM为正三角形.考虑到AO与x轴所夹锐角为60°,以AO为边构造正△AOC,则C(-4,0)(如图4).此时,△AOC与△AQM形成旋转相似形,从而△ACM∽△AOQ,于是
∠ACM=∠AOQ=30°.
由此可知,CM所在直线与x轴成固定夹角30°,当点Q沿y轴运动时,点M沿直线MC方向运动.故点M的运动轨迹是直线MC,且MC是AO的中垂线.下同思路1.
思路4也可基于△AMP进行思考.如图5,在y轴上取点D,使
∠OAD=∠AOD=30°.
构造另一对旋转相似三角形△AOD与△APM,从而
△AMD∽△APO,
于是
∠ADM=∠AOP=120°.
由于点D为定点,DM所在直线与线段AD成固定夹角120°,因此得到点M的运动轨迹是直线l,且由∠ADC=∠ODC和AD=OD,得MC为AO的中垂线.下同思路1.

图5 图6
2.4 旋转变换
思路5延续思路3和思路4可联想到旋转变换性质:旋转保持任意一个角的大小不变,或者说,角度是旋转下的不变量[2].如图6,△AQM是正三角形,点M可看作是点Q绕点A顺时针旋转60°后的对应点.当点Q在y轴上运动时,点Q的轨迹是一条直线.点Q的对应点M的运动轨迹也应是一条直线.理由如下:在y轴上任取一点Q′,以点A为旋转中心,将△AOQ′顺时针旋转60°得到△ACM′,则
△AOQ′≌△ACM′,
从而
∠ACM′=∠AOQ′=30°.
说明直线CM′是一条定直线,且与线段AC所夹锐角为30°.由∠ACO=60°,得∠MCO=30°,说明直线CM′与y轴的夹角为60°.
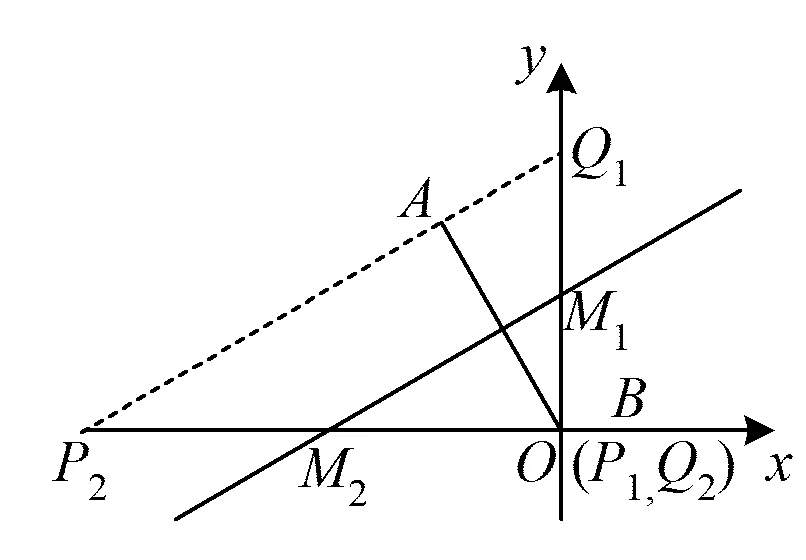
图7
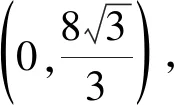
2.5 点线距离
从代数角度分析,平面直角坐标系中动点M的位置随点P,Q的变化而变化,但点P,Q的坐标存在关联.可考虑设参数,从而将第二空转化为用代数方法求点B,M之间距离的最小值的代数问题.据此得到思路6.
思路6如图7,设P(2a,0),Q(0,2b),M(a,b).由K字相似知
即
得
从而

则点B到该直线的距离即为BM的最小值
2.6 两点距离
上述在求线段最值时,均先确定动点轨迹,再运用“垂线段最短”公理解决问题.若轨迹一时难以确定,则可用“两点间距离公式”,形成思路7.

梳理以上7种思路,绘制结构化思维图(如图8),可以发现解题思路的产生需要在已知条件和结论之间展开丰富的联想,与旧知识、旧经验进行关联是解题思维形成的关键步骤.本题中由已知条件进行“斜中线定理”“线段中垂线性质定理逆定理”“平面内两点间距离公式”等联想,便于形成解题思路,更好地实现理解和迁移.
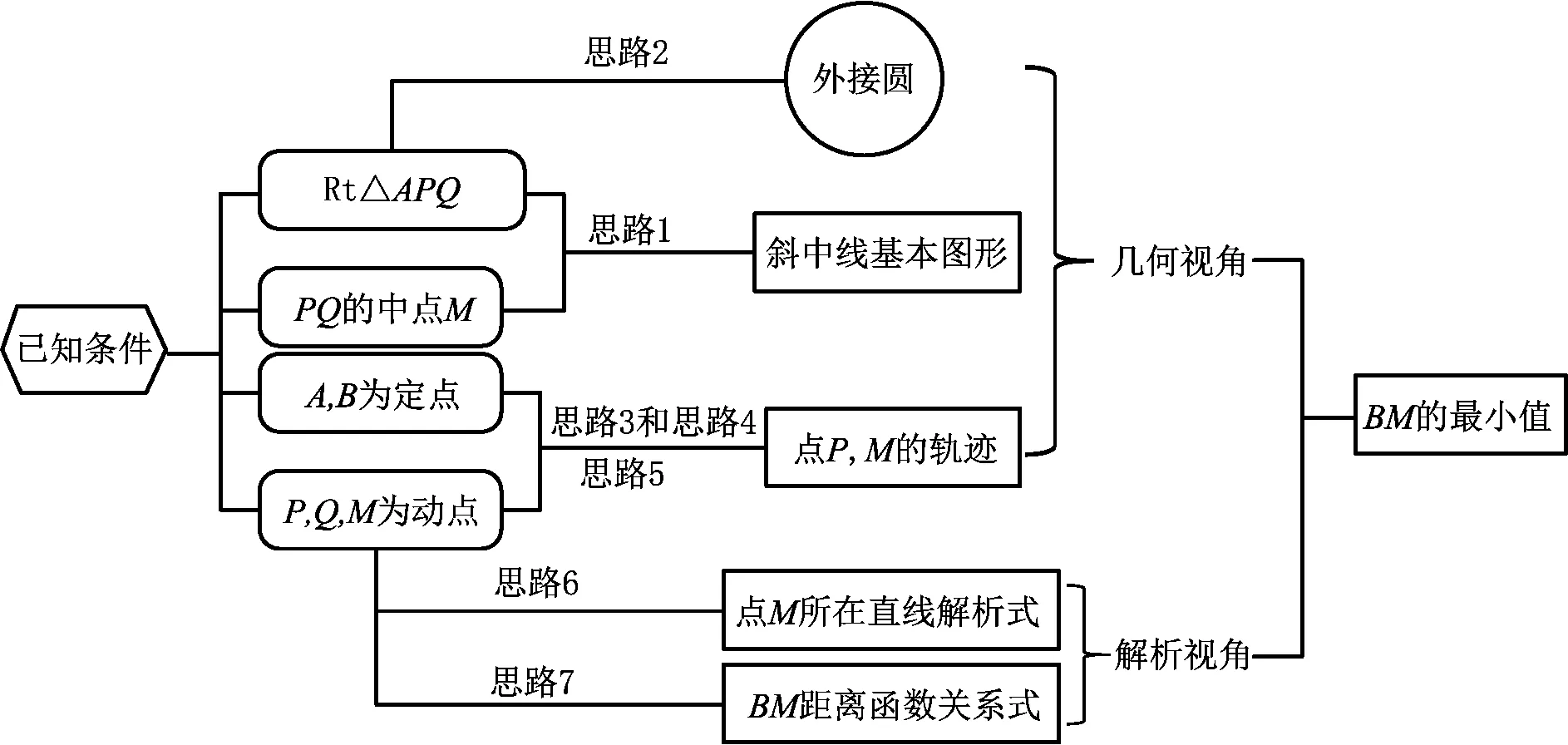
图8
3 探源
通过解题研究挖掘试题背后蕴藏的数学观点、数学思想.品味此题多种解法,颇觉思维开阔、齿颊芬芳、回味无穷;探觅源泉,更感精思巧设、灵动鲜活.
3.1 教材
典型图形“共斜边两个直角三角形”源于浙教版《数学》八年级上册第70页第6题:

图9
例2如图9,已知AD⊥BD,AC⊥BC,E为AB的中点,试判断DE与CE是否相等,并给出证明.
将其置入平面直角坐标系背景,改变问题情境,考查学生的几何推理、逻辑推理与迁移能力.改编思路不可谓不精巧.
3.2 原理
几何公理要求BM的最小值,即求点B到直线MN的垂线段长度,将公理“垂线段最短”应用于此题,考查学生的逻辑推理能力及运用已有知识和技能在新的情境中解决问题的能力,符合《新课标》强调的核心素养培养的理念.
函数解析通过函数解析式刻画动点轨迹,将几何问题用代数方法求解,体现数形结合思想及解决动态类数学问题时几何与代数间的本质联系.
3.3 题源
例1源自2021年浙江省嘉兴市数学中考试题第16题:

图10
例3如图10,在△ABC中,∠BAC=30°,∠ACB=45°,AB=2,点P从点A出发沿AB方向运动,到达点B时停止运动,联结CP,点A关于直线CP的对称点为A′,联结A′C,A′P.在运动过程中,点A′到直线AB距离的最大值是______;点P到达点B时,线段A′P扫过的面积为______.
(2021年浙江省嘉兴市数学中考试题第16题)
第一空需要先探究点A的轨迹,再求弧上一点到所对弦的距离最大值.例1与例3中均涉及先确定轨迹再求最值.一直一曲、一求最小一求最大、相互呼应、形异质同,突出考查学生的逻辑推理能力,具异曲同工之妙.
4 关联
4.1 隐去坐标
改变背景,将平面直角坐标系隐去,动点变为动图形,即为2022年浙江省嘉兴市秀洲区数学中考二模试题第16题:
例4一副含45°和30°角的直角三角形纸板ABC和DEF按图11摆放,BC=DE=12,∠ABC=∠DEF=90°.现将点D从点B向点A滑动,边DE始终经过BC上一点G,BG=2.H是边DF上一点,满足DH=DG(如图12),当点E到达点G时运动停止.当点E到达点G时BD的长为______;在运动过程中AH的最小值是______.
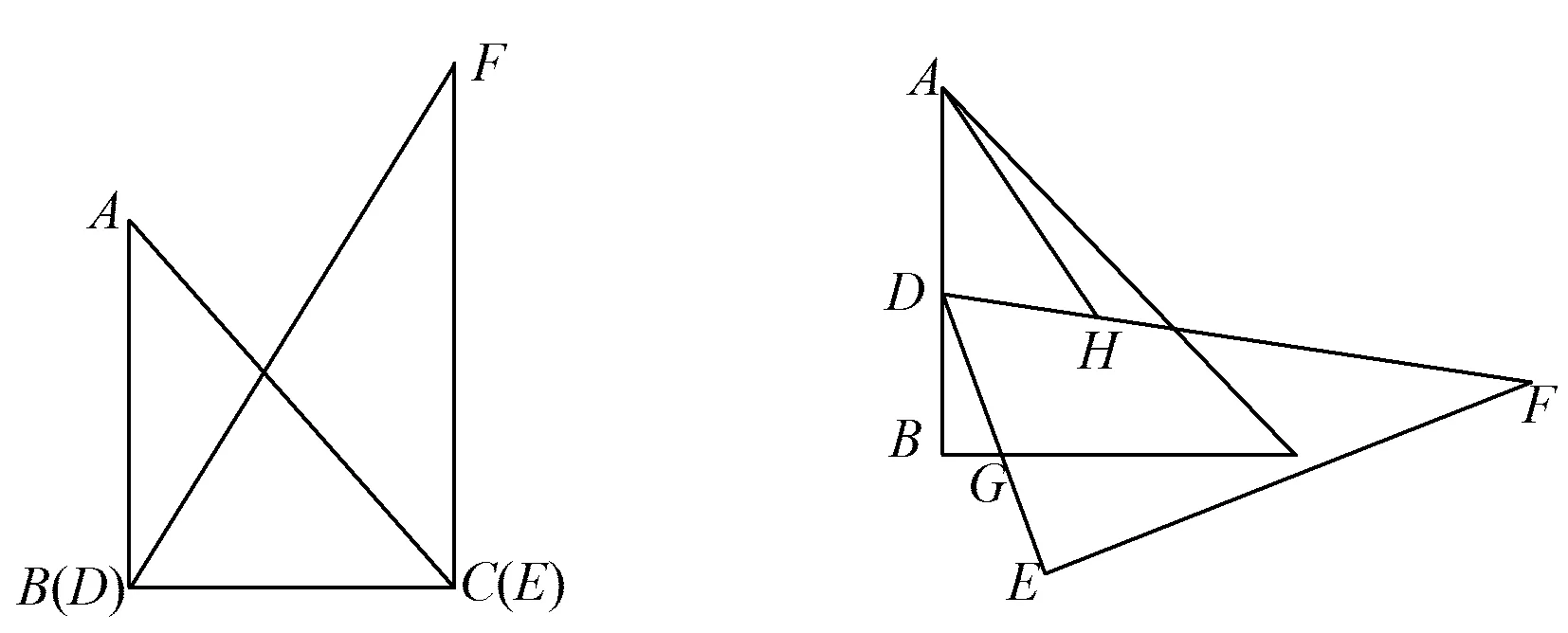
图11 图12
(2022年浙江省嘉兴市秀洲区数学中考二模试题第16题)
分析如图13,由已知得△DGH是正三角形,类比思路5的旋转变换策略,点D在线段AB上运动时,点H的运动轨迹是将线段AB绕定点G旋转60°后得到的线段所在的直线,线段的位置可由两个特殊值确定,从而线段AH的最小值转化为定点到定直线的垂线段长度.
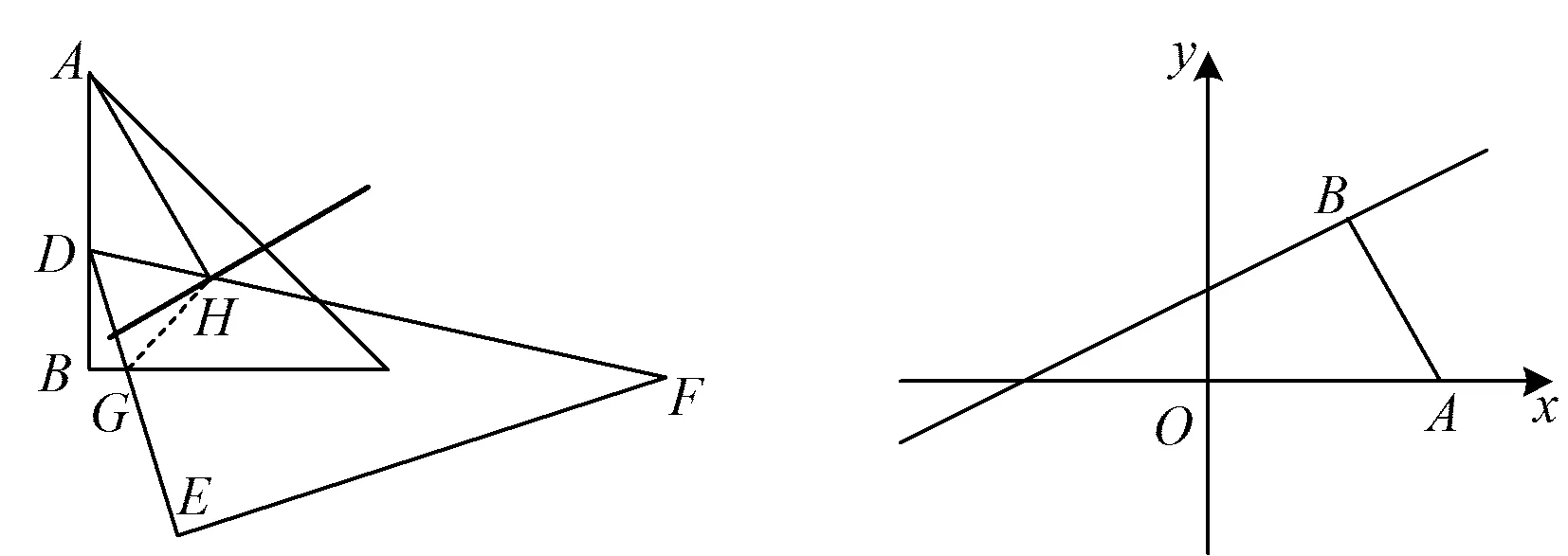
图13 图14
4.2 变旋转角
将图形置于坐标系,改变旋转角度60°为45°,即为2022年浙江省嘉兴市嘉善县数学中考一模试题第16题:
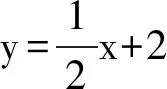
(2022年浙江省嘉兴市嘉善县数学中考一模试题第16题)

4x2+x2=9,
解得
于是
故

图15 图16
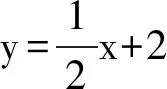
4.3 隐藏旋转
将题中的旋转隐藏,通过构造旋转相似解决问题,即为2022年浙江省嘉兴市海宁市数学中考二模第16题:
例6如图17,在△ABC中,∠ACB=90°,AC=2BC,以AC为边在其左侧作△ACD,联结BD.若AD=2,CD=4,则BD长的最大值为______.

图17 图18
(2022年浙江省嘉兴市海宁市数学中考二模第16题)
分析构造旋转相似形.如图18,以DC为直角边构造Rt△DCF,且满足DC=2CF,则
从而
△DCF∽△ACB.
由此可得
DC∶CF=AC∶BC=2, ∠DCA=∠FCB,
于是
△ADC∽△FCB,
故
由两点间线段最短,得
5 小结
求端点不定类线段的最值问题,可考虑两条路径:几何法与代数法.从几何角度来分析,如果该线段的一个端点是动点、另一个端点是定点,一般来说,需要将动点的运动轨迹先行确定,再运用相关定理求线段最值.从代数视角来分析,可运用设参法确定动点轨迹,或是直接用两点间距离求最值(如图19).

图19
克莱因曾说:“教师应该站在更高的视角来审视、理解初等数学问题,只有观点高了,事物才能显得明了而简单.”遇到好的典型问题,对其思路进行结构化梳理,寻找出通性通法,往往对促进学生数学解题能力发展有更好的效果,也促使不同的学生在数学学习上有不同发展,从而真正发展学生的核心素养.
