基于双层辉光离子渗金属的离子轰击金属靶材的计算机模拟

2023-02-02田林海姚晓红林乃明王振霞吴玉程

太原理工大学学报 2023年1期

李祥，田林海，2，姚晓红，林乃明，王振霞，秦林，吴玉程

(1.太原理工大学材料科学与工程学院，太原 030024；2.山西电子科技学院新能源与材料工程学院，山西临汾 041000；3.合肥工业大学材料科学与工程学院，合肥 230009)

双层辉光离子渗金属技术是在离子氮化基础上发展的表面冶金技术，具有设备简单、成分可控、节约材料、无污染、经济效益高等优点[1-2]，可形成具有各种功能的渗金属层以及薄膜沉积层。实现对双辉渗金属层及沉积薄膜的精确控制，关键在于靶材原子的溅射、输运和沉积过程[3]。离子轰击靶面时，同靶晶格发生能量交换，使其表面晶格崩溃，靶原子从各个方向飞出，当运动粒子在固体介质内穿行时，它与固体的原子核和核外电子相互作用，通过多次碰撞将其所有的能量传递给被击的靶粒子，而它本身的能量逐渐降低[4]。溅射事件本质上是一种先验统计学，在大量粒子轰击后，将会观察到重量变化等宏观效应。

长期以来，计算机模拟一直是研究高能离子与凝聚态物质的背散射、离子注入、辐射损伤和溅射等物理过程的重要工具[5]。溅射过程的计算机模拟可分为二体碰撞(BC)模拟、分子动力学(MD)模拟和蒙特卡罗(MC)模拟[6]。输运理论和蒙特卡罗模拟在原理上是等价的，碰撞的统计由泊松定律决定，碰撞截面和相互作用力作为主要输入。蒙特卡罗模拟几乎没有什么限制，但是大部分计算时间都消耗在一些无关紧要的碰撞事件上；二体碰撞模拟的独特之处在于引入了特定的靶结构，在计算速度上有巨大的优势，比分子动力学模拟大约快4～5个数量级[7]；分子动力学模拟是通过求解系统的牛顿运动方程来跟随粒子系统的时间演化策略[8]，计算机的计算能力将能量限制到较低的范围。本文首先对典型的双层辉光离子渗金属装置进行了建模，分析了离子抵达靶表面的能量范围，然后对金属靶材溅射过程进行了模拟，研究了靶材表面粒子溅射的能量和角度以及溅射产额的变化规律，以期对双层辉光渗金属和其它溅射镀膜技术提供一定的参考。

1 物理模型和计算方法

双层辉光离子渗金属装置示意图如图1所示，其本质上是两套二极型辉光放电系统，源极(溅射源)和工件极分别是两套放电系统的两个阴极，它们同时受到气体粒子的不断轰击[9]。

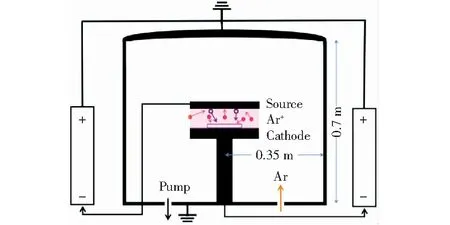
图1 双层辉光离子渗金属装置示意图Fig.1 Double glow plasma surface alloying equipment diagram

双层辉光离子渗金属装置整个内壁都接地，整体作为一个阳极。源极和阴极都需要考虑二次电子发射过程，所有电极都需要考虑吸附过程。将阴极电压加至-600 V，通过实验测得源极的悬浮电位为-28 V.在低气压无碰撞状态下，根据玻姆判据[10]，离子会以玻姆速度到达鞘层，如公式(1)所示。双层辉光离子渗金属工作气压较高，达到几十Pa，因此不能忽略碰撞，碰撞会使玻姆速度降低。

(1)

式中：uB为玻姆速度；e为离子电荷；Te为电子温度；M为离子质量。

将阳极设置为悬浮电位时，利用通量守恒方程以及玻尔兹曼关系式可以得出器壁电位如式(2)所示[10]，代入氩气(M=40 amu)数据，可得式(3)，将电子温度(Te)设置为5 V与实验测得数据较为接近。

(2)

式中：φw为相对于鞘层-预鞘层边界的器壁电位；m为电子质量。

φw=-4.7Te.

(3)

离子能量εi会以式(4)到达阳极表面，此时离子能量会小于或者接近于阈值(20～50 eV)，可以忽略阳极溅射。

εi=5.2Te.

(4)

VAHEDI et al研究了碰撞鞘内离子角分布的解析模型，得到了靶附近的离子平均速率，从而可以获得靶附近的离子平均能量如式(5)所示[11]：

(5)

式中：λi为离子平均自由程；V0为阴极位降；s为鞘层厚度。

根据加速电压分布的密度函数亦可计算出抵达靶材表面离子的平均能量，由式(6)给出[12]：

(6)

粒子的溅射过程模拟使用SRIM软件，采用二体碰撞近似的蒙特卡罗法模拟，其过程主要包括：自由飞行路径抽样、碰撞参数抽样、确定碰撞后粒子的运动方向。对于一个靶原子而言，受到大量入射粒子以不同的碰撞参数的撞击事件，将其归一化为概率关系，将入射粒子与固体中的某个原子发生碰撞的概率称为碰撞截面。SRIM采取的简化主要是用一些解析式或数值当量替代散射积分式(7)。

(7)

式中：Θ为离子的最终散射角；r为碰撞过程中两原子的距离；V(r)是两个原子的原子间势能；p为碰撞参数；Ec是质心系动能。

需要选择合适的平均自由飞行路径，以保证即使在较低的能量下也能满足反冲原子的转移能量T大于给定阈值Tmin.当入射离子能量很低时(小于数百电子伏特)，由于离子轨道的下一个偏转点在靶原子前，其自由飞行路径小于与下一个靶原子之间的距离，此时使用硬球碰撞来近似，通过与实验进行对比，硬球碰撞近似能够提供足够精确的估计[13]。在低能量时，自由飞行路径为：

(8)

式中：N为靶的原子密度。

在质心系下，一个质量为M1、能量为E的入射粒子，在一个排斥力的相互作用势下，通过一个质量为M2的初始静止粒子的散射，如图2所示。

图2 质心系粒子的轨迹Fig.2 Locus of the center of mass

BIERSACK et al[14]提出了一个MAGIC公式(9)来代替散射积分式(7)，它的计算速度提高了50倍。

(9)

(10)

ρ=ρ1+ρ2,δ=δ1+δ2.

(11)

式中：p为碰撞参数；a为屏蔽半径；r0为最接近点的距离；Δ是能够平稳地拟合慢速离子在屏蔽库仑势下的散射结果；ρ1、ρ2为最接近点的轨迹曲率半径；δ1和δ2为很小的修正项。

SRIM程序基于无定形靶的假设，所有表面原子都在一个光滑的平面，对于具有晶粒随机取向的靶，方向效应大部分被补偿[14]。入射离子和反冲原子在其减速过程中被跟踪，直到它们的能量下降到预定能量(Tmin)以下，通常设入射离子的阈值为5 eV，反冲原子的阈值为表面结合能。SRIM程序为了加快计算速度，检查反冲原子是否移动到离表面很远的地方、或者损失了很多的能量，放弃跟踪不能抵达表面的反冲原子。

2 模拟计算结果及讨论

2.1 物理参数的选择

在给定温度与气压后，离子平均自由程为定值，靶材附近的离子平均能量与阴极位降V0和鞘层厚度s有关，为了简化计算，将双层辉光等离子渗金属装置模型设为二维轴对称，源极和工件极从三维圆形极板抽象为长为0.1 m宽为0.005 m的长方形。选取典型的双辉渗金属工艺参数进行模拟，源极电压设为-900 V，阴极电压设为-600 V，气压为40 Pa.

图3为使用COMSOL模拟在给定工作参数下，工作腔室等离子区的初始电势和达到稳态时的电位分布。当达到稳态时，主等离子体区电势呈现电中性，在直流辉光放电的模拟中主要是针对阴极鞘层区，因为在整个辉光放电区域中，只有阴极附近存在强电场，带电粒子在阴极位降区的运动主要是电场作用下的迁移运动[15]。

图3 工作腔室等离子区的电势分布Fig.3 Potential distribution in the plasma region of working chamber

取稳态电势的中心截线进行绘图，如图4(a)所示，对于双层辉光离子渗金属设备，更关心稳态电位时两极板间中心截线部分如图4(b)，再进行局部放大如图4(c)所示。当离子速度趋近于玻姆速度时，预鞘层与鞘层之间会出现奇点，如图4(d)所示。

RIEMANN[16]研究了平行平板碰撞的预鞘层以及其他几种不同的预鞘层的解析解，发现不同的预鞘层在奇点附近的特性很相似。由图4(b)及(c)可以得出阴极位降约为-835.62 V，鞘层厚度约为7.12 mm，可得离子的平均能量约为191.72 eV.即使不考虑碰撞造成的能量损失，离子抵达靶表面的能量最大为：

图4 稳态电位时的电位分布Fig.4 Potential distribution at steady-state potential

(12)

由于Te约为数伏，可以忽略不计，代入数据可得离子抵达靶表面最大的能量约为835 eV.靶材的溅射阈值20～50 eV[10]，本文主要研究轰击离子能量50～1 000 eV对靶材的溅射。此能量范围的轰击离子能量恰好全部处于单一撞击溅射范围，由于参与碰撞事件的原子数量有限，溅射主要由初级和次级反冲原子控制，发生的少量碰撞通常不足以像线性级联模式那样随机获得动量[17]。

2.2 溅射原子信息

沉积在衬底表面的原子的能量对溅射沉积过程中形成的膜的结构有重要的影响，在溅射原子到达衬底之前，将与背景气体发生碰撞造成能量损失，而溅射原子的能量和角度在很大程度上影响了结构、晶粒取向、孔隙率等因素[17]。为了优化渗金属过程，需对溅射粒子的能量和角度分布信息进行研究，本文通过蒙特卡罗模拟使用重复抽样来获得某些现象的统计特性，对较多的碰撞事件进行统计分析的结果能够更好地逼近真实的物理过程。对于研究靶材的溅射，只有朝向靶表面的反冲是重要的，可以选择单个薄靶来模拟溅射过程，这样可以减少对溅射无贡献的反冲时间。利用SRIM软件，选取不同能量的Ar+在相同位点垂直轰击镍靶，抽取第1-1 000个溅射原子的信息进行统计，如图5所示，高能量的离子产生的溅射原子更加分散。对于入射粒子，除了弹性碰撞造成的能量降低之外，入射粒子还必须要有足够的能量摆脱晶格的束缚才能继续前进，所以高能量的粒子能够抵达更远的地方。处于最外层的溅射粒子能量通常很低，可能是由于飞行路径较长，通过碰撞损失的能量较多，在大量的模拟实验下，边缘附近的溅射原子的能量会略高于表面结合能。

图5 溅射原子的位置分布Fig.5 Position distribution of sputtered atoms

以溅射原子的位置信息作为X、Y轴，能量信息作为Z轴，得到不同位置溅射原子的能量分布如图6所示，可以看到高能量的溅射原子数量极少，溅射原子的能量主要集中在20 eV内。

图6 溅射原子的能量分布Fig.6 Energy distribution of sputtered atoms

能量为200 eV的Ar+以不同的角度轰击靶材产生的溅射原子的能量信息，如图7所示。入射粒子的角度在0°～40°范围内，溅射原子的能量分布对入射角度不敏感，对于入射粒子的角度在60°～89°范围内的溅射原子的能量随着角度的增加而有增加的趋势，即溅射原子能量出现在几个电子伏特到十几个电子伏特的能量范围内的频率降低，在较高能量范围的频率增大，推测可能是沿X轴分量较少，可能经历较少的碰撞就能够与表面附近的靶原子发生碰撞，从而入射粒子保留较多的能量。

图7 不同的角度轰击下溅射原子的能量分布Fig.7 Energy distribution of sputtered atoms under different angle bombardment

利用溅射原子的方向余弦信息来表示其方向，并将起点全部移动到坐标原点位置，如图8所示。其中的黑色矢量是靶材表面法线方向的单位矢量，极少数溅射原子可能出现较大的角度。当其出现很大的角度时，溅射原子的能量在X轴上的分量必须要大于其表面结合能才能摆脱束缚成为溅射粒子，否则将不能脱离表面。

图8 溅射原子方向Fig.8 Direction of sputtered atoms

取10 000个溅射原子的方向向量信息与黑色矢量求解向量角，并进行区间统计，如图9所示。溅射原子的方向与黑色矢量夹角主要集中在0 °～60 °之间，随着入射粒子的能量的增加，小角度以及大角度出现的频数都略微增加，较高能量的入射离子大角散射截面减小，但最大转移能量增加，初级反冲原子能量在靶间的高效耗散，使大量的原子具有足够的能量被发射出去，当溅射原子处于小角度时，在X轴的分量较大，更容易脱离表面。

图9 溅射原子的角度分布Fig.9 Angular distribution of sputtered atoms

2.3 溅射产额的变化规律

图10是在不同能量的Ar+垂直轰击下，原子序数为22-30的靶材溅射产额。可以发现，随着靶材原子d壳层电子填满程度的增加，溅射产额增加[18]。

图10 不同靶材的溅射产额随Ar+能量的变化Fig.10 Changes of sputtering yield of targets with Ar+ bombardment energy

图11是在相同的初始位置不同能量的Ar+垂直靶表面轰击靶材的溅射产额，在达到较高的能量前，溅射产额随着能量的增加而增加，且在低能量区域增加较快，当离子能量达到30 keV时，这时溅射产额随离子能量的增加而降低，这种现象通常被认为是由于轰击离子此时深入到晶格内部，其大部分能量损失在靶内，而不是在靶表面的缘故[18]。

图12是本文SRIM模拟值与一些溅射产额实验测量值[5，19-20]的对比，不同的实验测量结果虽略有差异，但SRIM的模拟结果趋势能够与实验测量值较好地拟合。目前，广泛采用WEHNER et al[20]的溅射率的测量值。他们在测量溅射率时把入射离子的离子电流近似地看作是靶电流，如果考虑靶放出来的二次电子，实际的溅射率为测量值的(1+f)倍，其中f为二次电子发射系数，WEHNER et al的测量值略小于真实值。

图11 溅射产额随Ar+能量的变化Fig.11 Change of sputtering yield with bombardment energy of Ar+

图12 SRIM模拟值与实验测量值的对比Fig.12 Comparison of SRIM simulation values with experimental values

图13是能量为200 eV的Ar+以不同的入射角轰击镍靶的溅射产额信息。当入射角从20°增加到60°时，溅射产额单调增加，入射角在60°附近时达到最大值，当入射角再继续增加，溅射产额急剧减小。同时，与溅射产额急剧减小相对应的是溅射原子的平均能量会单调增加，如图14所示。在大入射角情况下，碰撞集中在离表面极近的表层范围内，由于入射离子的背散射使碰撞不能充分扩大，其结果是低能碰撞反冲原子的生成效率急剧下降[21]。

3 结论

对双辉等离子渗金属技术中的轰击离子的产生和输运过程、以及离子对靶材的溅射过程进行了探究，利用辉光放电的理论以及COMSOL Multiphysics软件对双辉等离子体渗金属设备进行了建模，得到稳态时二维平面电势的分布图，利用Vahedi的碰撞鞘层的解析模型获得抵达靶材表面离子的平均能量的解析公式。使用COMSOL模拟的电势图结合辉光放电理论分析了阴极位降大小，利用玻姆鞘层判据以及主等离子体区准电中性的特性分析鞘层厚度，其阴极位降模拟值与理论上相近，鞘层厚度与实验中测量相符。