基于路径-博弈混合策略的无人机空战机动决策*

张瀚文 ，甘旭升 ，魏潇龙 ，童荣甲

（1.空军工程大学 空管领航学院，陕西 西安 710051；2.中国人民解放军94188 部队，陕西 西安 710077）

0 引言

随着无人机技术的发展，越来越多的有人机任务可被无人机替代，不断加剧战场的无人化进程［1］。特别是在空战场领域，有人-无人协同作战概念发展迅速，使得空中作战样式更为丰富，进一步增加了空战在现代作战中的地位作用［2］。其中，无人机空战一直是世界各国研究的焦点，一旦走向实战将彻底颠覆现代空战作战理念。但由于无人机自主决策能力的不足，无人机空战始终无法走向实战，成为限制无人机作战应用的一大制约因素［3-4］，对此，国内外都展开了广泛研究。

文献［5］使用粒子群算法和人工势场法相混合的方法实现无人机空战机动决策，实现了一对一空战的机动决策，决策规划空间在三维空间内实施，但决策时长接近1 s。文献［6］使用模糊数学的思想改进基本博弈决策机制，提出基于直觉模糊的空战博弈决策算法，算法可在7 类机动动作间选择决策，结合改进差分进化算法求解最优混合策略。但单纯基于博弈策略仅能基于局部信息进行决策，缺少全局信息的考虑。文献［7］通过生物免疫算法实现无人机的自主决策。免疫算法主要是通过模仿生物的免疫记忆过程实现算法的自学习功能，但该算法在较大空间内的规划决策效率较低，算法效率受规划空间影响显著。文献［8］在空中态势判断基础上基于纳什均衡理论实现敌机目标的分配，可实现多机协同空战。但同样只能利用局部信息进行决策。文献［9］使用改进的Q-learning 算法实现无人机的机动决策，基于态势信息矩阵进行多机目标协同，实现了多机空战机动决策。但文中只对目标分配规划效率指标进行了说明和优化，对单机机动决策的综合耗时并未进行详细说明。文献［10］使用神经网络实现无人机的空战机动决策，但对神经网络的训练始终是技术的难点，想要进行完备的训练和持续的优化具有较大的难度和工作量，若训练不够充分将持续影响决策品质，导致空战失利。文献［11］使用改进强化学习算法实现无人机的空战决策机动，通过加入启发式因子的方式提升学习算法寻优性能，具有一定参考价值。文献［12］则是提出了一种基于强化遗传算法的空战机动决策算法，通过分类器的设计可改进传统遗传算法只能对显式目标进行建模的缺陷，但该文对最终的规划效率问题分析不透彻，而空战问题对规划效率有较高要求。

综上所述，当前对无人机空战机动决策问题普遍采用了神经网络、仿生算法、强化学习、博弈论等方法，但在三维空间内进行规划决策过程中，因为规划空间较大，在规划效率与规划品质方面往往难以兼顾。本文将针对无人机空战机动决策问题，基于强化学习和博弈理论提出一种混合算法，实现高效的机动决策。

1 飞行控制模型

无人机飞行控制模型是将机动决策指令转换为机动动作的技术基础。无人机空战机动过程主要是垂直和水平方向上的机动，状态的改变主要通过仰角、航迹偏角和速度的改变实现，控制量主要为滚角、转弯率和推力变量。由此可以得出运动学方程为

式中：v为无人机速度；γ为无人机仰角；β为无人机航迹偏角。

无人机的动力学方程为

式中：m为无人机质量；L为无人机升力；F为无人机最大推力；η为无人机的推力系数；μ为无人机滚角；D为空气阻力。

阻力、升力的计算方法又可以表示为

式中：q为动压；S为机翼面积；ρ为空气密度；Cd为阻力系数；Cl为升力系数。控制变量为

式（1）～（4）中部分变量根据机型性能具有一定约束范围，可表示为

2 空战机动战术策略

空战机动决策指令的形式必须要以现实空战战术需求为基础，否则无法达成期望的战术目的。敌我无人机在进行空战对抗过程中，所做出的机动动作均是为了在规避敌方火控雷达锁定和电子干扰的同时，将对方使用火控雷达锁定，并发射空-空导弹击毁敌机。机动方法主要是水平方向机动和垂直方向机动，其中水平机动更为重要。因为空战对抗的空间范围可发生在上百千米水平面内，但垂直空间范围却在20 km 范围内，相对而言，垂直机动范围要狭窄得多，在进入近距空战前，垂直机动的效果有限。但为了避免进入近距空战前丢失势能优势，在水平机动过程中应当保持高度上的优势。因此，敌我双方在空战对抗过程中，机动策略应当分别制定。

本文将敌方火控雷达照射范围假设为一个椎体，且具有一定作用距离。我方无人机在水平面上的机动应当避开敌机航迹水平投影方向上的扇面投影范围，并使敌机进入我机火控雷达照射范围，如图1 所示。

图1 水平机动策略Fig.1 Horizontal maneuver strategy

在垂直方向上，应当尽可能地保持高度势能优势，同时也利用垂直机动进入敌机火控雷达盲区，对敌机进行锁定，如图2 所示。

图2 垂直机动策略Fig.2 Vertical maneuver strategy

图2 中：ΔH为红蓝方高度差；θf为红方火控雷达辐射角度。当无人机被对方火控雷达锁定，则在每一个时间步长内都有一定概率被击落，以红方无人机为例展开介绍，攻击命中概率计算可表示为

式中：θrb为红蓝方航向相对角；d为红蓝方无人机之间的距离；为红方无人机的火控雷达辐射角，其作用角度范围为为红方无人机的火控雷达作用距离。红蓝方航向相对角θrb如图3 所示。

图3 无人机角度关系Fig.3 Angle relationship of UAVs

图3 中，υr为红方无人机航向向量，υrb为红方无人机空间坐标指向蓝方无人机空间坐标的向量。θrb的计算方法为

式（6）中的σb用于判断蓝方是否对红方实施了电子干扰，假设电子干扰范围假设与火控雷达工作范围一致，则计算方法为

3 空战机动决策算法

本文根据敌我双方空战对抗的基本战术策略，构建空战机动模型，由于无人机的水平机动控制和垂直机动控制可以进行解耦［13］，因此本文将机动决策过程同样进行分离，先进行水平机动决策，再进行垂直机动决策。

3.1 水平机动决策算法

3.1.1 水平机动动态栅格环境构建

在以往基于路径规划的无人机机动决策研究中［14-15］，三维空间内的机动决策必须同等建立三维栅格环境，而后才能进行路径规划与机动控制。三维栅格环境具有建模简便的优点，但也具有显著的缺陷：一是规划空间庞大，会使规划速率大幅下降；二是规划空间静态，无法适应空战对抗高分辨率、高不确定性、对抗范围广阔的需求。对此本文在水平、垂直决策相互解耦的前提下设计水平动态栅格环境。水平动态栅格环境与敌我双方的相对水平位置有关，红蓝方在栅格环境中的栅格坐标始终不变，栅格坐标根据红蓝方位置旋转变化，栅格分辨率根据相对距离自适应调整，如图4 所示。

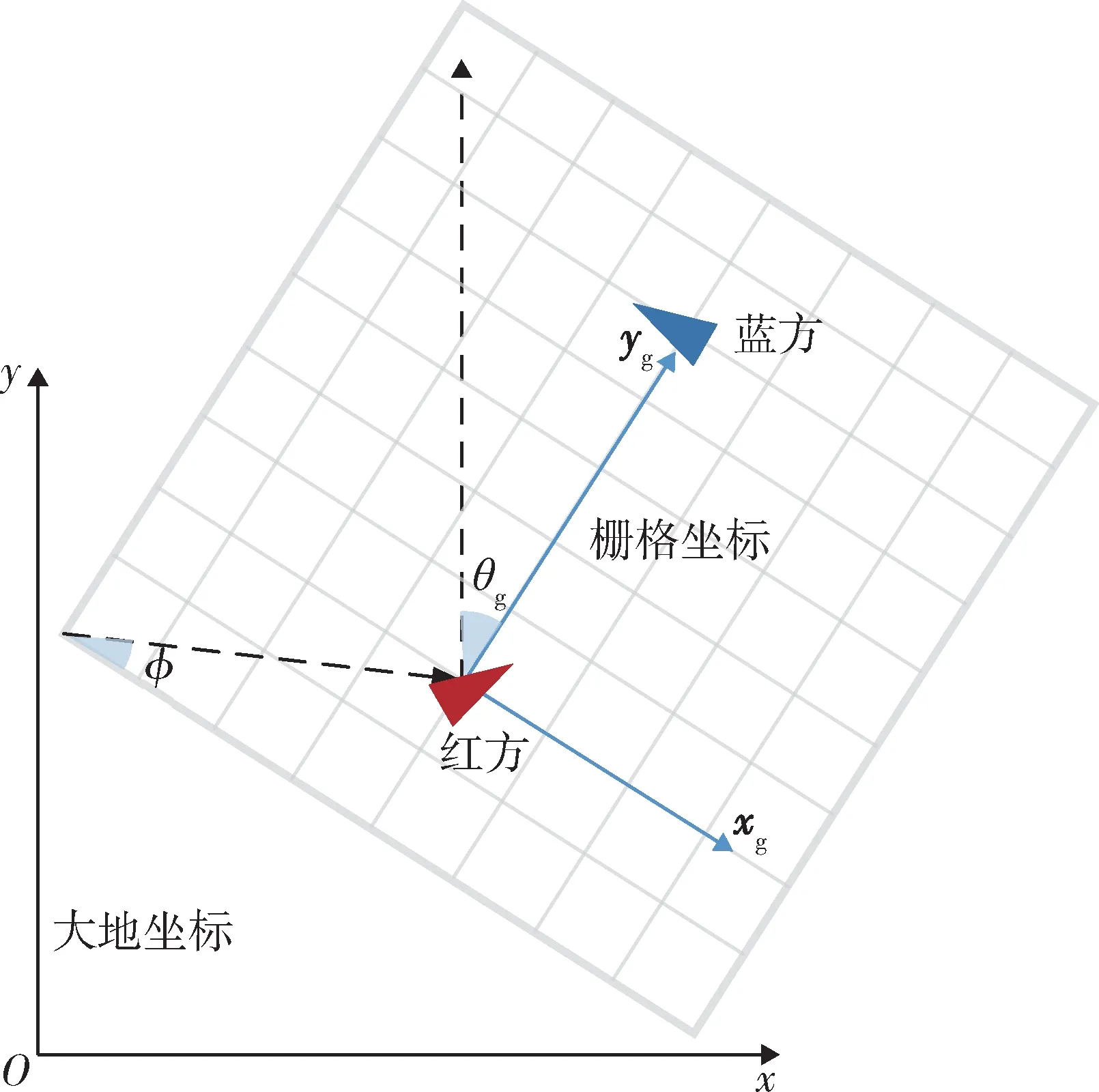
图4 动态栅格环境Fig.4 Dynamic grid environment

规定动态栅格坐标与大地坐标之间的旋转角顺时针方向为负，则坐标变换公式为

式中：θg为栅格坐标与大地坐标之间的交角；（xg，yg）为某一栅格坐标；（x，y）为转换后对应的大地坐标；ϕ为无人机在栅格坐标中的位置向量与x轴形成的夹角，逆时针旋转为正。

3.1.2 基于改进Q-learning 的机动决策

Q 学习（Q-learning，QL）算法是一种离轨策略下表格型的学习算法，由Watkins 提出［16-17］。在QL 算法中，学习机制的实现是通过Q 表来实现的，表格的列代表了智能体的转移规则，行代表了智能体的多种状态，表格中的每一个空格都用以记录智能体的学习信息，信息的更新公式可表示为

式中：α为学习率；γ为折扣因子；s为当前时刻的状态；a为当前时刻按策略π采取的动作；s'为下一时刻的状态；a'为在s'状态下能够获得最大回报的动作。智能体在Q 表中各个状态之间的转移按照随机策略（ε-贪婪机制）进行转移，学习机制则通过奖励和惩罚实现［16］。由于智能体在每一步的转移过程中只基于当前状态信息，对全局信息利用率不足，会影响最终解的质量。在每一轮的智能体寻优过程中，对前期的学习信息并未加以利用，可能导致大量的无效学习过程，降低规划效率。因此，应当对基本QL 算法做出改进，提升学习质量。本文使用双Q 表算法（double Q-learning table algorithm，DQLT）记录agent 的探索记录。计算步骤为：

step 1：使用启发式因子初始化后的Q1表进行探索。启发式因子为状态点与目标点之间的距离信息，距离越近，初始奖励值越高。

step 2：开始新一轮探索，记录智能体每一次的探索过程，直至达到满足单轮学习的结束条件。结束条件可以是智能体达到目标点，也可以是探索步数达到规定值，避免陷入重复学习探索。

step 3：根据当前轮次的探索学习记录，输出一条路径信息，并将路径信息记录于Q2表，使用Q2表信息覆盖Q1表。

step 4：重复step 2～3，直至达到迭代次数。

step 5：输出最后一次生成的路径方案。

改进算法通过2 张Q 表的交替使用，使得智能体在探索过程中能够充分利用已有学习信息，持续提升学习质量。启发式因子的加入又减少了无效学习过程，加快收敛速度。

基于输出的规划路径，无人机做出水平机动决策。若规划路径的第1 步为左转、直行或右转，则无人机做出左转、直行或右转的机动动作。

3.2 垂直机动决策算法

本文使用博弈策略实现无人机在垂直方向上的机动决策，首先应当建立支付函数。对于垂直方向上的优势判断并非一成不变，而是与态势关系紧密相关，因此需要分情况讨论。本文将其划分为3类情况进行讨论。

（1）威胁区内，未将敌机锁定，未被敌机锁定

此时无人机需要水平机动占据有利地位的同时，还需要积极取得势能优势，用于必要时候转化为动能优势，进行快速机动。但这一优势并非无限扩大，只需要适当保持，若高度差过大，会影响对敌机的攻击。支付函数可表示为

（2）威胁区内，将敌机锁定

由于已经将敌机锁定，此时无人机应当尽可能将敌机控制在火控雷达照射范围内，因此应当缩小高度差，争取更多雷达锁定时间。支付函数可表示为

式中：τ3为常数。

（3）威胁区内，被敌机锁定，且未锁定敌机由于已被敌机锁定，应当尽可能通过机动脱离火控雷达照射区域，此时的机动方向与敌机相对角大小成正比，越大越好。支付函数可表示为

式中：τ4为常数；为红方第i种策略下蓝方无人机指向红方无人机的向量；υb为蓝方无人机的方向向量。

若红蓝方无人机仍在威胁区之外，则不进行垂直机动，只进行水平方向机动前出接敌。由此构建无人机空战博弈支付矩阵，可表示为

式中：x1，x2，…，xm为红方无人机采取策略；y1，y2，…，yn为蓝方无人机采取策略；frmn为红方第m种策略与蓝方第n种策略对抗下的支付函数值。在此假设红方无人机只进行3 类垂直机动，分别为拉升、平飞和俯冲，则它的一个混合策略为

式中：

则可得出红方的纳什均衡值可表示为［18］

由于垂直机动样式较少，因此对于混合策略的求解可以直接以遍历的方式求出近似最优策略。

3.3 基于路径-博弈混合策略的空战机动决策

本文使用了在水平方向与垂直方向相互解耦的飞行控制模型，该模型并非所有机型都能够适用，与飞机的气动布局、飞行速度、使用需求等因素都相关，但该模型有效性已被大量研究所验证［9，12，19］，因此具有一定合理性与现实意义。根据解耦的机动决策策略，本文使用改进QL 算法实现水平机动决策，使用纳什均衡理论实现垂直机动决策，最终得出综合的机动决策指令，机动决策混合算法流程如图5 所示。

图5 机动决策混合算法流程图Fig.5 Flow chart of hybrid algorithm for maneuver decision-making

4 仿真验证

论文仿真试验主要基于Matlab 7.1 进行开发，所用电脑处理器为Snapdragon（TM）850，Win10 系统。开发环境对计算效果会有一定影响，但不影响算法性能对比。针对红蓝方单机对抗的情景进行仿真，验证算法的有效性，算法基本参数设置如表1所示。

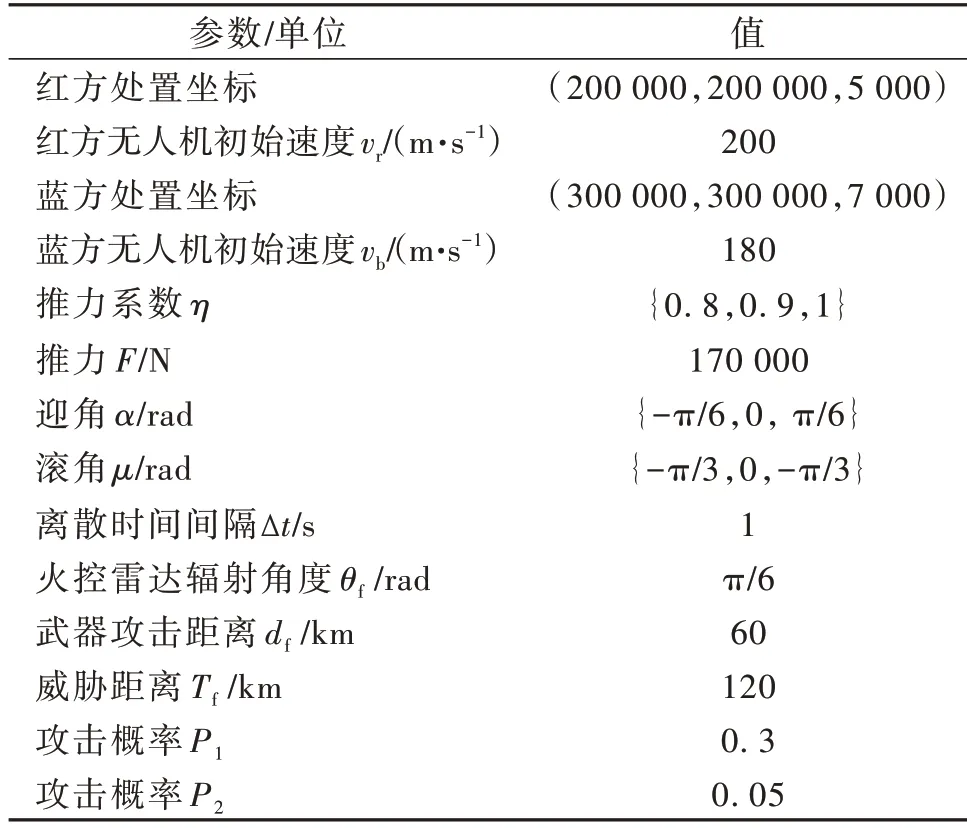
表1 参数设置Table 1 Parameter setting

根据决策算法输出结果，水平机动的输出为左转、直行和右转，对应控制变量滚角为-π/3，0，-π/3；垂直机动输出上升、平飞和下降，对应控制变量迎角为-π/6，0，π/6；推力变量则根据态势来输出，分为威胁区外、威胁区内和被敌机锁定3 种状态，对应推力系数为0.8，0.9，1。

先进行水平机动决策算法验证，同时验证QL算法和改进QL 算法的决策效果。在栅格内的规划路径效果如图6 所示。

图6 算法路径规划对比Fig.6 Algorithm comparison of path planning

为体现改进QL 算法在动态对抗环境中的决策性能优势，本文在二维平面内开展空战对抗仿真验证。但单次空战对抗胜负具有偶然性，因此需要进行多伦空战，通过胜率体现算法的性能。单次空战对抗仿真如图7 所示。

图7 二维平面空战对抗仿真Fig.7 Two-dimensional air combat confrontation simulation

通过20 次空战对抗仿真，查看2 种算法胜率变化，如图8 所示。

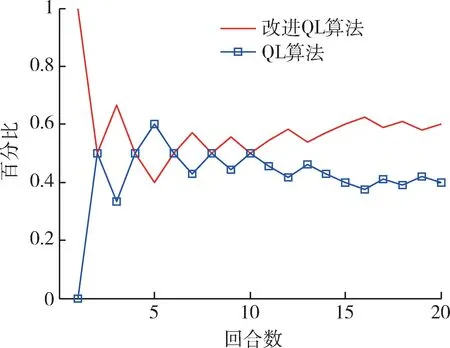
图8 胜率变化曲线Fig.8 Winning rate change curve

通过多次的对抗试验可以发现，在二维平面内，改进QL 算法具有更优的机动决策性能，最终胜率约为0.6，显著高于原有算法。

进一步在三维空战对抗环境中对2 种算法的使用效果进行对比，如图9 所示。

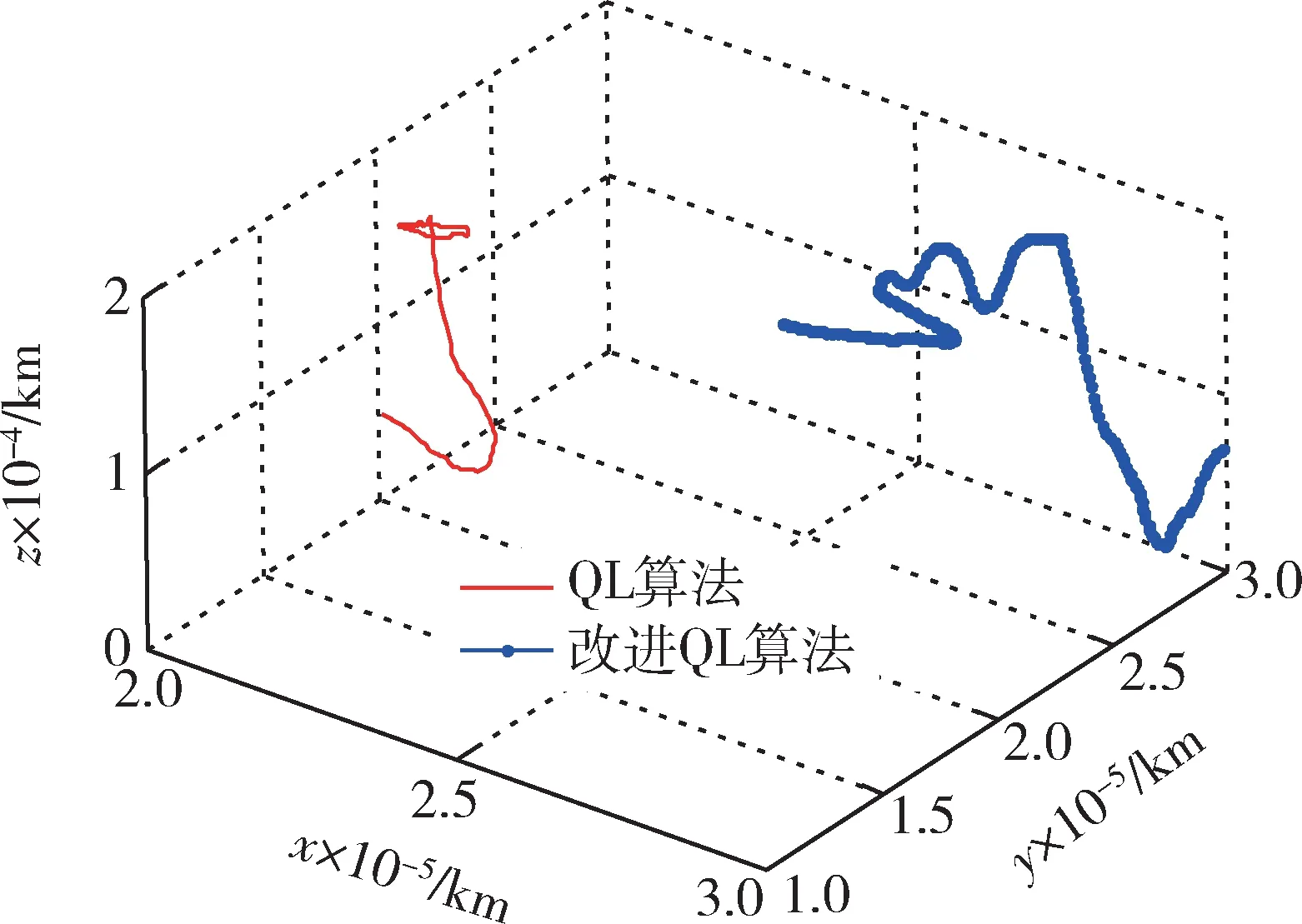
图9 空战机动决策算法效果对比Fig.9 Effect comparison of air combat maneuver decision-making algorithms

从图9 中可以看出，基本QL 算法因为较低的学习品质，会有很多误决策，导致陷入不利态势而被敌机击落。算法的垂直机动决策耗时如图10 所示。

图10 垂直机动决策耗时Fig.10 Vertical maneuver decision-making time

从图10 可知，垂直机动用时很少，机动决策的主要耗时在水平机动上，也是更为关键的技术内容。在此，进一步引入一种较为经典的路径规划算法——蚁群算法（ant colony algorithm，ACO）来作为对比研究，对抗过程中，蚁群算法作为红方无人机，使用静态三维栅格环境规划路径，改进QL 算法作为蓝方无人机，对抗效果如图11 所示。

从仿真机动效果来看，2 种算法都具有较好的决策性能，但从规划用时来看，改进QL 算法具有更显著的优势。

ACO 算法与改进QL 算法的综合规划时间对比如图12 所示。

图12 决策算法综合耗时对比Fig.12 Comprehensive time comparison of decisionmaking algorithms

从图12 中可以看出，改进QL 算法规划时间均可控制在1 s 之内，而蚁群算法则基本在3 s 以上。通过将垂直方向与水平方向的决策行为进行解耦后，可在保持较好决策效果基础上，有效缩短决策时间，提升空战对抗中对不确定情况的应对能力。

5 结束语

本文使用垂直与水平决策相解耦的方式来实现无人机的空战机动决策。使用双Q 表学习的方式改进基本QL 算法，提升智能体学习质量，实现无人机的水平机动决策；使用纳什均衡理论实现无人机的垂直机动决策。针对无人机一对一空战对抗的情景，使用仿真验证了本文提出算法的有效性，对比传统使用三维静态栅格环境规划路径的算法，可有效缩减规划规模，加快规划速度，提升决策算法的战场适用性。