基于线性自抗扰控制的重型多轴特种车辆防抱死制动控制研究
2023-02-01程洪杰何星磊刘志浩杨健福
程洪杰,何星磊,刘志浩,高 蕾,杨健福
(火箭军工程大学 导弹工程学院,西安 710025)
重型多轴特种车辆是保证特种装备机动性、灵活性、安全运输的重要工具之一,是战斗力的基本保证。由于车身长、惯性大、轴数多、用途特殊以及运输环境复杂多变等特点,存在制动时间和距离长,制动稳定性差,易发生车轮抱死甩尾侧翻等问题。而ABS是在制动过程中防止车轮被制动抱死,提高车辆的方向稳定性和转向操作能力,缩短制动距离的安全装置。因此,为保证重型多轴特种车辆在紧急制动、高速避障等极端工况下的制动稳定性和可靠性,要求其ABS控制算法具有更强的适应性和鲁棒性[1]。
目前ABS主要控制策略有:逻辑门限值控制、滑膜变结构控制、比例积分微分(proportion integration differential,PID)控制、模糊控制和模糊PID控制等[2-4]。逻辑门限值控制策略算法易于实现,应用广泛,但其控制参数单一、系统波动很大,难以达到很好的控制效果[5-6];LU等[6]利用Adams及Simulink进行直线制动测试,在附着系数0.8的路面以100 km/h的初速度开始制动,结果表明,采用逻辑门限值控制器的ABS滑移率在制动全程波动较大,在完全制动前不能达到稳定状态。滑模变结构控制鲁棒性强,适合用于非线性控制,且其系统控制的参数及扰动无关,但抖振现象无法避免,只能进行优化消除[7-8];He等将滑模变结构控制算法导入电动汽车,在水泥路面进行50 km/h的紧急制动试验,结果表明,制动稳定性有所提升,但抖振现象仍无法消除。PID控制策略,算法虽然易于调试,但对被控对象参数变化敏感,鲁棒性不足,参数整定多通过试凑法,缺乏理论依据支撑;More等[9-10]利用Simulink搭建了单轮防抱死控制模型,通过PID控制将85 km/h直线紧急制动的滑移率控制在0.2左右,但响应速度较慢,且参数整定不好确定。模糊控制可以根据经验需求进行控制,鲁棒性较好,但需要根据大量经验建立控制规则,自适应能力差,较难实现;Pramudijanto等[11-12]将神经网络-模糊(neuro-fuzzy,NF)控制与PID控制进行了对比,结果表明,NF控制响应速度更快,但超调量也较大。每种算法都有自己的优缺点,后来一些学者通过取长补短,将控制算法结合起来,设计出了控制效果更好的控制器;凌滨等[13-14]设计了模糊PID防抱死控制器,并在不同的附着系数路面进行了ABS仿真分析,结果表明,模糊PID控制的防抱死制动效果比PID控制效果更好。综上所述,传统的ABS控制,由于汽车路况和车况复杂,在制动过程具有非线性、时变性和不确定性等特征,从而使得超调量与响应时间难以兼得。因此,要想ABS系统在保证制动效果的前提下,制动过程能快速、稳定及强抗扰,需要从根本上入手。
Han等[15]提出了非线性自抗扰控制(nonlinear active disturbance rejection control,LADRC)控制,利用非线性跟踪-微分器获得微分信号并实现过渡过程的配置,利用非线性扩张状态观测器(linear extended state observer,LESO)估计实时估计系统的状态和扰动信息,利用非线性组合控制率实现非线性状态和扰动的状态反馈,从而把充满扰动、不确定性和非线性的被控对象还原为标准的积分串联型,实现了扰动的主动抑制和消减。但LADRC调试参数较多,调节复杂,且参数与控制性能的对应关系不明确,参数调节麻烦且无明显规律可循,在实际应用中难以简单快速地实现控制目标[16-17]。Yuan等[18],将NADRC简化为LADRC结构,并把自抗扰控制的所有参数都变为带宽的函数。这样简化和参数化后,不仅物理意义更为直观,而且使得自抗扰控制的调参数大幅减少到2~3个,引导了大批学者投身其中,产生了一系列的控制理论与工程应用成果,并有望取代传统 PID 控制算法[19-20]。
针对传统ABS存在的滑移率非线性、时变性和参数不确定性等问题,本文设计了一种基于滑移率的ABS二阶LADRC控制器,采用扩张状态观测器实时观测和估计系统中内、外扰动的总扰动,并通过线性比例-微分(proportion differential,PD)反馈控制律补偿扰动对被控对象输出的影响。通过与模糊PID控制的单轮ABS试验对比分析,验证了LADRC控制的优越性。在高、中、低附着系数路面,以初速度60 km/h进行了重型多轴特种车辆的ABS联合仿真,验证了LADRC控制在ABS应用上的可行性和优越性。
1 单轮ABS数学模型
单轮ABS数学模型包括单轮动力学模型、滑移率模型、轮胎模型、制动器模型和控制器模型。ABS数学模型结构如图1所示。
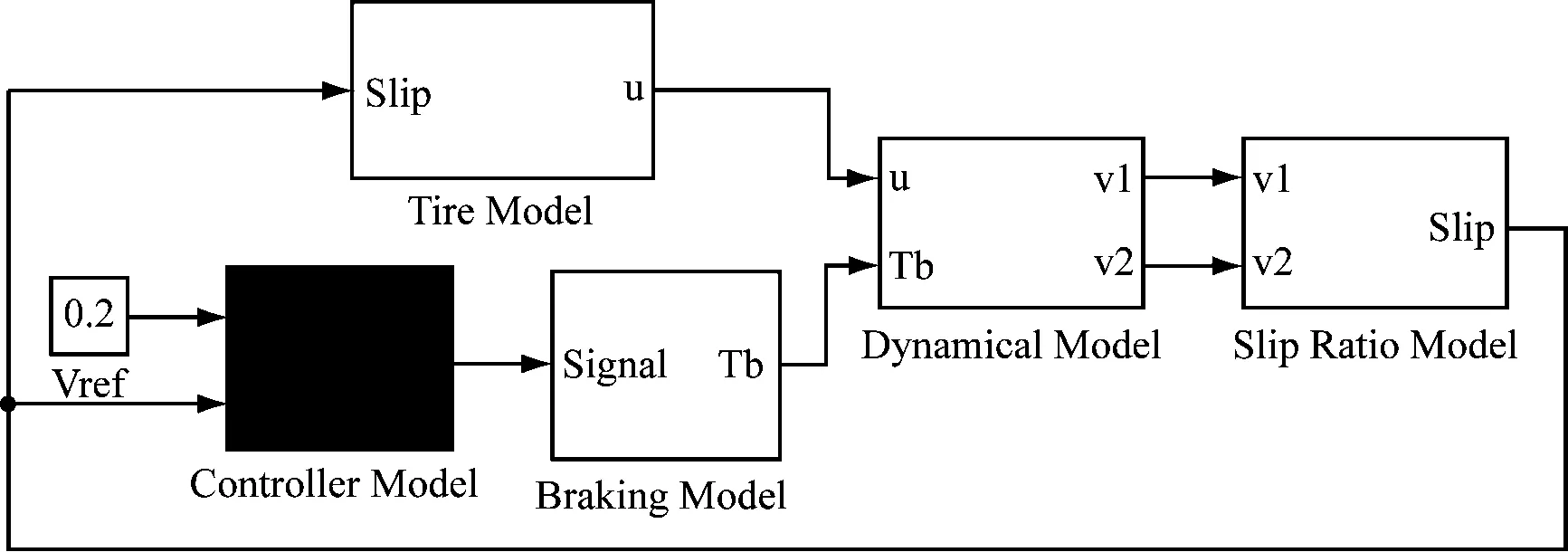
图1 单轮ABS数学模型结构Fig.1 Single-wheel ABS mathematical model structure
1.1 单轮动力学模型
考虑到重型多轴特种车辆整车动力学模型过于复杂,为简化分析与计算,建立单轮动力学模型,如图2所示。
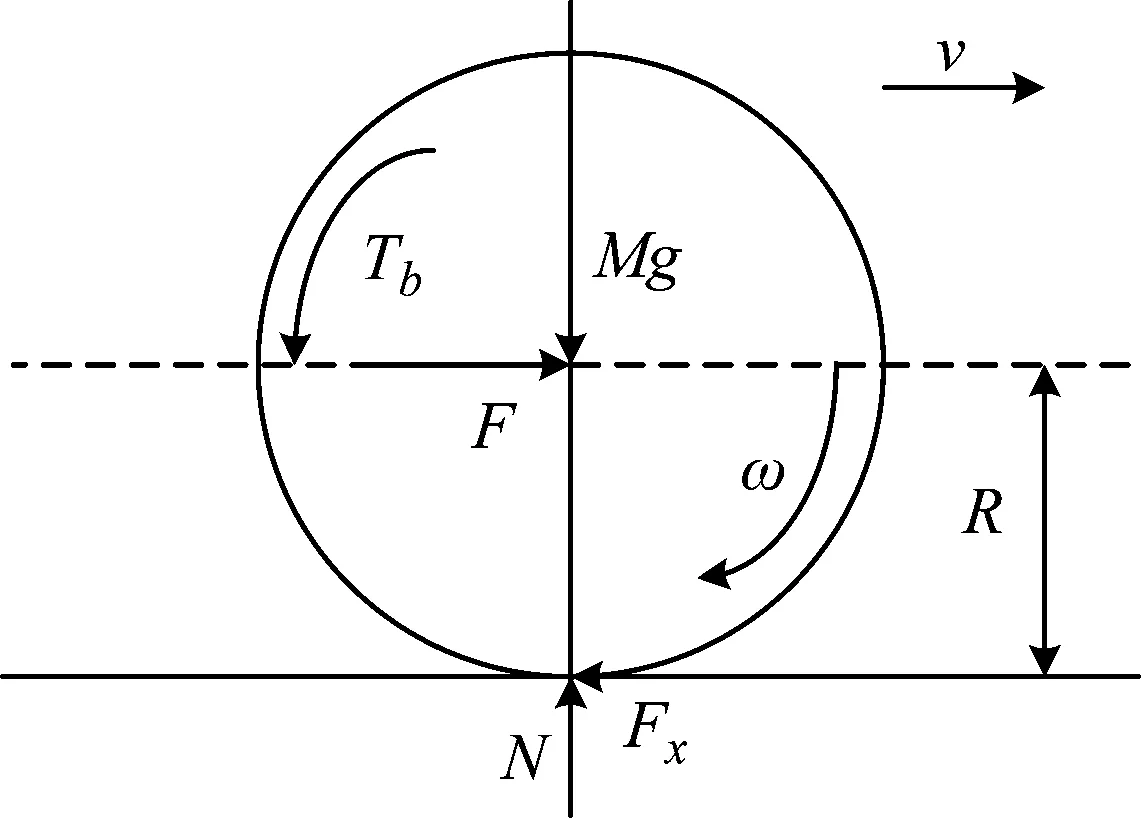
图2 1/10运动车辆单轮受力情况Fig.2 1/10 Stress condition of single wheel of moving vehicle
重型车运动方程
(1)
车轮运动方程
(2)
车轮所受纵向力
Fx=μN
(3)
车轮所受垂直载荷
N=Mg
(4)
式中:M为1/10车身质量(kg);v为车身行驶速度(m/s);Fx为地面制动力(N);ω为车轮角速度(rad/s);R为车轮半径(m);Tb为制动器动力矩(N·m);g为力加速度(m/s2);I为车轮转动惯量(kg·m2);N为车轮所受的垂直载荷(N);F为驱动力(N);μ为地面附着系数,与滑移率λ有关。
1.2 滑移率模型
在整车刹车制动过程中,随着制动力矩的提高,车轮的滚动比例部分减少,滑动比例部分增加。一般用滑移率λ表征滑动的程度。
滑移率λ定义为
(5)
当滑移率λ=0时,车轮的速度等于车身的速度,则车轮是纯滚动;当λ=1时,车轮的速度为0,则车轮是纯拖滑;当0<λ<1时,则车轮是边滚动边滑动。
1.3 轮胎模型
轮胎作为整车与路面直接接触的部件,其仿真性能直接影响整车动力学特性,因此轮胎模型需反映车轮对地面的附着系数μ与滑移率λ之间的关系,如图3所示。本文轮胎模型采用经典的轮胎魔术公式,三种典型路面魔术公式参数经验值如表1所示[21]。轮胎路面附着系数魔术公式表达式为
μ(λ)=Dsin{Carctan[Bλ-E(Bλ-arctan(Bλ))]}
式中:D为峰值因子;C为曲线形状因子;B为刚度因子;E为曲线曲率因子;μ(λ)为附着系数;λ为滑移率。
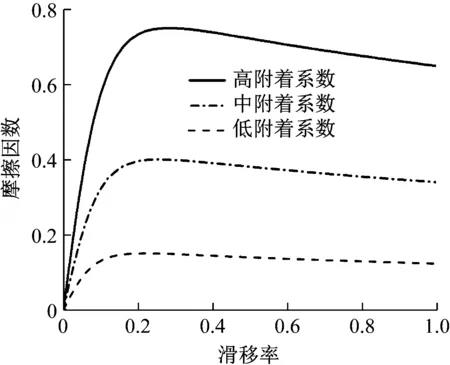
图3 路面附着系数与滑移率的关系Fig.3 The relationship between adhesion coefficient and slip rate
1.4 制动器模型
制动器力矩Tb与制动器气压压力P的关系模型为
Tb=KfP
(6)
式中:Kf为制动器制动因数(N·m/kPa);P为液压压力(kPa)。
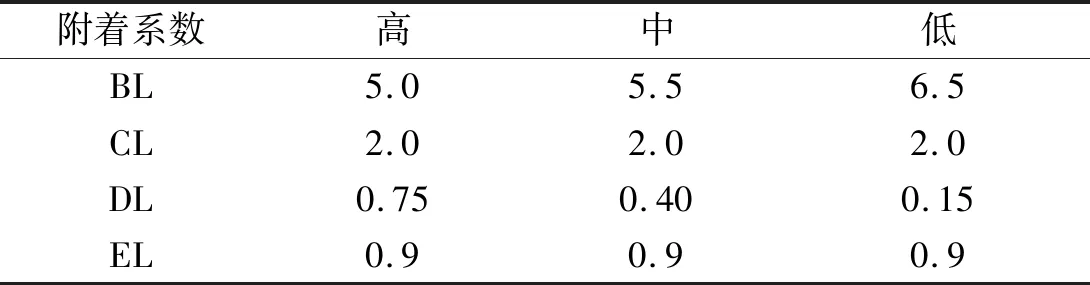
表1 三种典型路面魔术公式参数经验值Tab.1 The empirical value of three typical road magic formula parameters
滑移率λ和气压压力P分别为气压传动系统输入和输出。传动系统各机械部件的间隙和摩擦,会引起滞后及显著非线性动态特性,将系统理想化为一阶惯性环节和一个积分环节级联
(7)
式中:K为气压制动环节放大的系数,一般取100;τ为气压环节的时间常数,其参数漂移是引起制动力矩扰动的内因,一般近似取0.01 s。
式(6)和式(7)为复频域气压制动模型,可推导出时域气压制动模型
(8)
式中,滑移率λ在ABS控制过程动态变化,故气压制动系统是关于制动转矩Tb的非线性系统。
1.5 LADRC控制器模型
自抗扰技术将外部扰动和参数偏离引起的内部扰动的扩张综合为总扰动,通过反馈补偿方式抑制扰动,适用于内外扰动共存的汽车防抱死制动控制。
根据式(1)~(8)得控制器的状态方程为
(9)
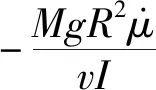
2 面向ABS的LADRC控制器设计
LADRC由跟踪微分器(traction differentiator,TD)、线性扩张状态观测器(linear extended state observer,LESO)和线性状态误差反馈控制律(linear state error feedback,LSEF)组成。TD主要是用于微分信号的获取和过渡过程的配置,LESO利用系统的输入、输出来估计系统的总扰动,LSEF用于控制量的生成,同时对扰动进行补偿。
2.1 线性扩张状态观测器设计
传统的ADRC都是采用非线性函数,调节参数多,调节耗时且复杂。本文针对车辆防抱死系统,设计了面向ABS的LADRC控制器,由于现在已经有了成熟完善的过渡过程配置手段,因此在设计中略去了TD配置过渡过程部分。LADRC控制框架如图4所示。
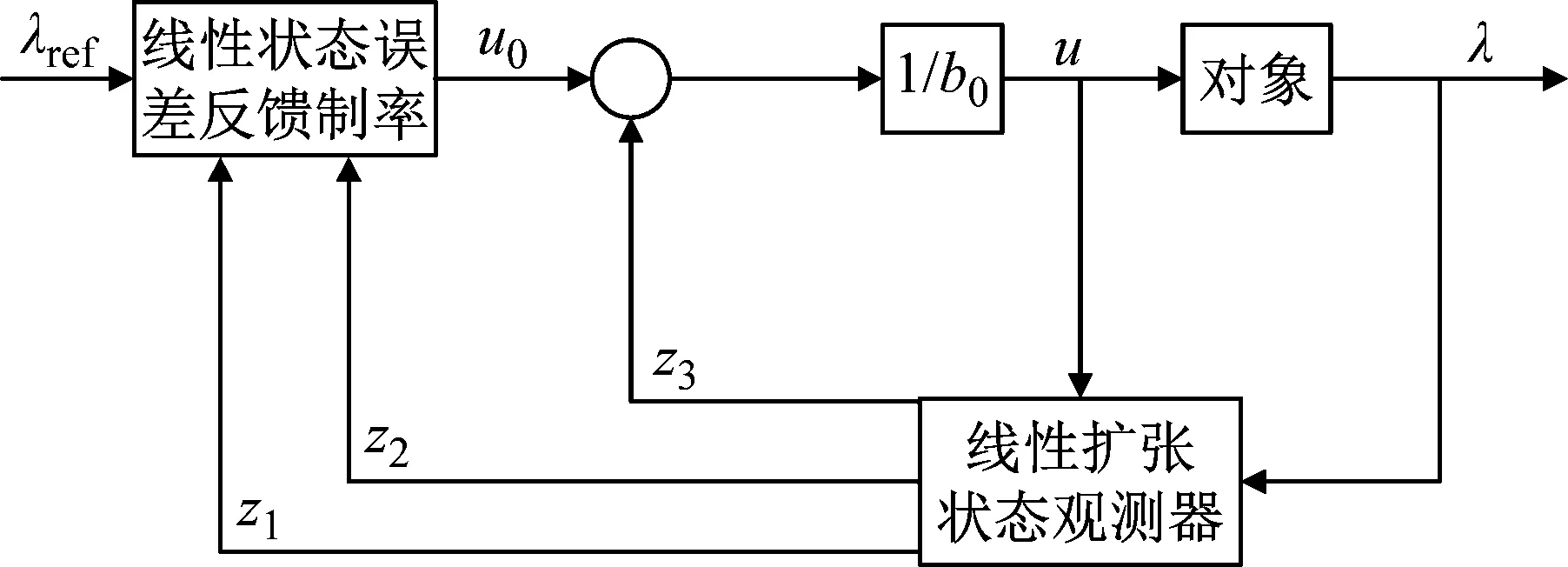
图4 LADRC控制结构框图Fig.4 LADRC control structure block diagram
图4中,λref为设定的期望滑移率,LESO输出的z1、z2、z3分别为对滑移率λ、滑移率的微分λ以及总扰动f的观测量,u0为PD控制律的输出量,b0为待调参数,u为被控对象的控制量。
对于LESO的设计可以利用ADRC几乎完全不依赖对象的特点,设计全阶无对象模型的LESO,但是在对ABS系统LESO的设计中可以获得部分对象模型的信息,将这些已知的模型信息可以集成到扩张状态观测器(extended state observer,ESO)中,设计模型辅助的LESO,从而减轻ESO的计算负担,并提高扰动的估计精度,从而提高控制效果。
(10)
式中:u,λ分别为输入与输出;w为扰动;a0,a1以及w均已知;f为包含了外扰动和内扰动的总扰动。

(11)
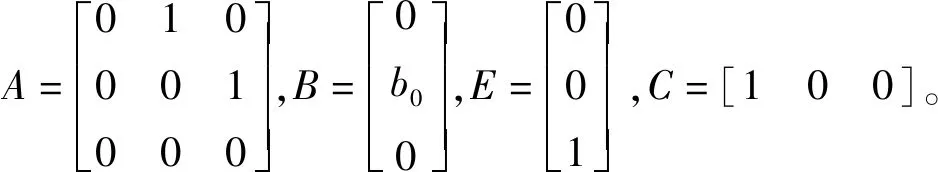
对应线性连续线性扩张状态观测器(LESO)为
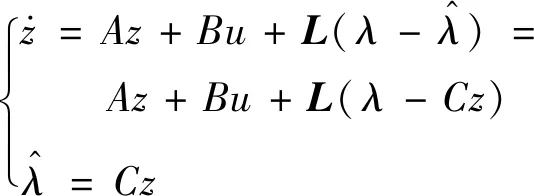
(12)
式中:z→x,z为观测器的状态向量;L为观测器的反馈误差增益矩阵,需要设计。
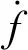
观测器方程调整为
(13)
式中:uc=[uλ]T是组合输入;λc是输出;z=[z1z2z3];A、B、C的取值同式(11);L为LESO的增益矩阵。
经过参数化,可把特征方程的极点放在同一个位置(-w0,w0为观测器的带宽)上,即取观测器的增益矩阵为
使得:
λ(s)=|sJ-(A-LC)|=(s+w0)3
式中:J为单位矩阵。观测增益矩阵与观测器的带宽唯一相关,使得连续LESO的设计变得简单。
2.2 线性状态误差反馈控制律设计
由于LESO能够实时估计并补偿外部与内部的扰动,因此传统PID中在常值扰动下为消除静差而采用的积分器已不再需要,所以LSEF可以采用PD控制器的形式。
u0=kP(λref-z1)-kdz2
(14)
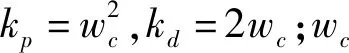
这样PD控制器参数唯一与控制器带宽相联系,使得控制器的参数整定变得便捷。带宽越宽,高频成分通过的多,输出的复现精度就越高,控制系统的性能就越好。但是,带宽过高会引入传感器的高频噪声,而且还会引起谐振,因此,选择合适的带宽很重要。通常对于大部分工程对象w0=(2~10)wc。
通过LESO,被控对象中扩张出的代表扰动的状态变量x3(即f)被状态变量LESO的z3跟踪,通过消减z3(即z3)将被控对象变成一个双重积分器串联单位增益的控制问题。由式(13)和式(14)可得ABS系统的控制量
(15)
3 单轮ABS试验验证
本文利用合肥工业大学单轮ABS控制算法测试平台,在高附着系数路面以初速度为30 km/h进行单轮ABS试验,通过模糊PID控制和LADRC控制的ABS制动效果对比分析,验证LADRC控制的可行性和优越性,单轮ABS台架试验图如图5所示。该试验台架由1/10车辆道路模拟试验系统和线控制动系统两部分组成。1/10车辆道路模拟试验系统为制动试验提供不同路面附着系数,主要由飞轮、磁粉离合器、扭矩传感器、滚筒组、电机、车轮和1/10车辆载重台架组成。线控制动系统主要由机械制动器(mechanical regulation brake,MRB)、可控电流源组成,通过对轮速和车速信号进行采集与处理,完成对MRB的制动力矩的控制[22]。

图5 单轮ABS试验台架Fig.5 Single wheel ABS test bench
3.1 试验模型
单轮ABS试验台架系统模型原理框图如图6所示,利用Labview搭建了单轮ABS试验控制模型,由路面附着系数模拟系统模型和制动控制器模型两部分组成,分别如图7和图8所示。
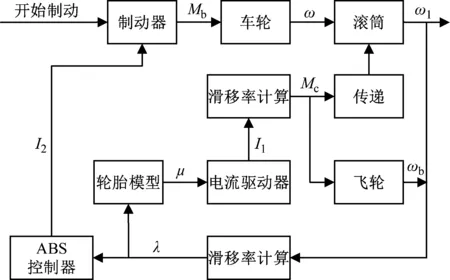
图6 单轮ABS试验台系统模型原理框图Fig.6 Block diagram of the system model of the single-wheel ABS test bench
3.2 试验结果与分析
试验得到速度曲线(车速和轮速)、滑移率曲线和制动距离曲线,如图9所示。具体结果如表2所示。
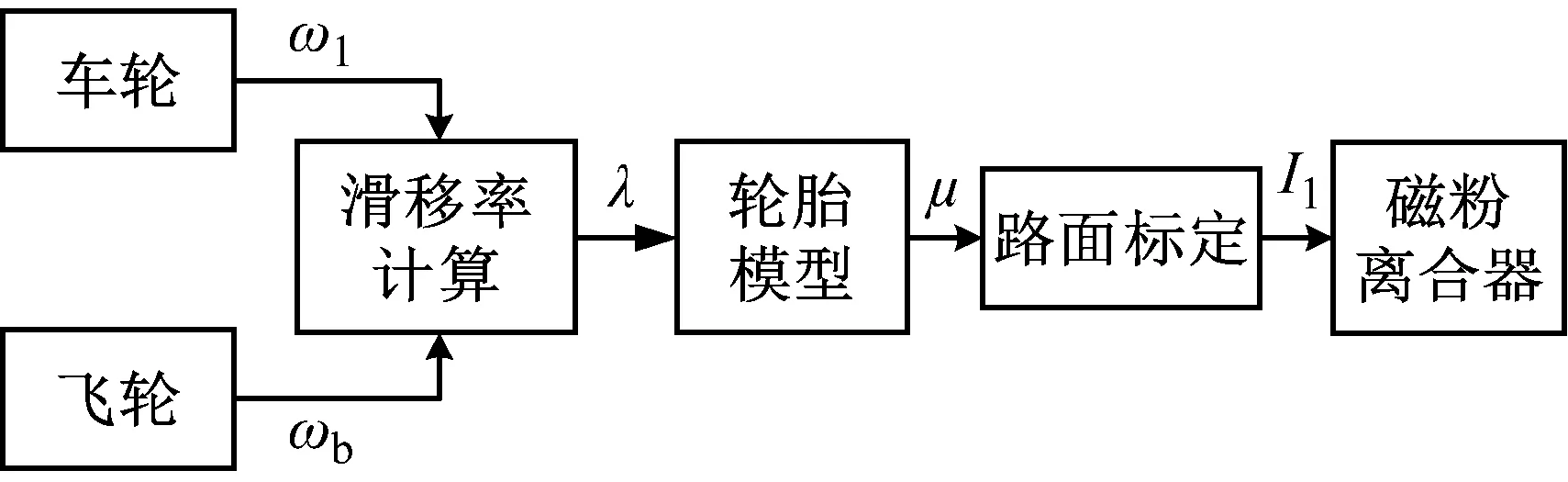
图7 路面附着系数模拟系统原理图Fig.7 Schematic diagram of the road adhesion coefficient simulation system
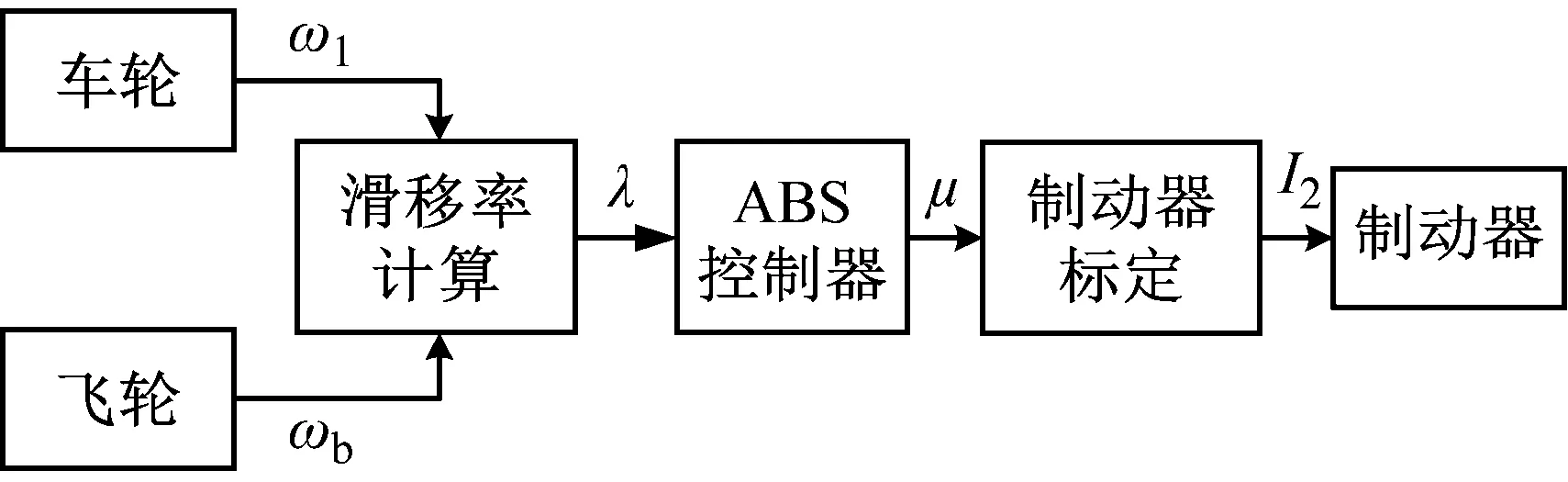
图8 控制器模型原理图Fig.8 Schematic diagram of the controller model
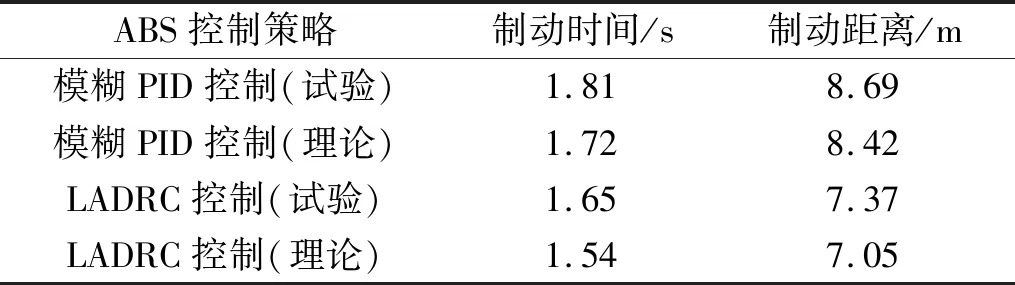
表2 仿真结果对比Tab.2 Comparison of simulation results
由图9和表2可知,在相同的条件下,单轮ABS台架的试验数据与Matlab/Simulink仿真的理论数据非常接近,验证了试验数据的正确性。
数据表明:(1)与模糊PID控制相比(图9(a)),在理论条件下,ADRC控制的制动时间和制动距离分别缩短了0.18 s(10.4%)和1.37 m(16.3%);在试验条件下,单轮LADRC控制的制动时间和制动距离分别缩短了0.16 s(8.9%)和0.32 m(15.2%)。
(2) 图9(b)表明,在理论和试验条件下,车速与轮速基本同步减小,未发生轮胎抱死现象,两种控制算法都能稳定减速停车,避免了安全事故发生。
(3) 图9(c)表明,两种控制算法下,达到最佳滑移率0.2时,滑移率波动都比较小,没有出现大的超调量,且LADRC控制的ABS到达最佳滑移率的响应速度快,波动幅度小。
分析表明:图9分别从制动时间、制动距离和滑移率三方面对比了LADRC和模糊PID的控制效果,对比表明,LADRC控制单轮防抱死制动控制明显优于模糊PID控制,具有更佳的制动效果。
4 整车建模
整车模型主要包括:①车身系统:包含车体尺寸参数和质量及转动惯量信息。具体参数有车身长宽高、轴距、轮距、质心高度、车轮静力半径,整车转动惯量等等;②轮胎系统:Trucksim软件可选的轮胎模型种类较多,本文选择内部简单车轮外倾模型,所有车轮均为单胎,轮胎基本参数根据实车设计要求选定;③悬架系统:一般包括悬架运动特性和弹性运动特性参数设置,即KC整车试验特性曲线;④转向系统:主要包括方向盘与转向系统中可转动部分的转动惯量、转向机以及与其连接部分的转动惯量;⑤动力传动系统:建立发动机外特性曲线,设置离合器、变速器和差速器参数;⑥制动系统:采用气压式制动系统,制动器采用鼓式制动器。设置制动力矩曲线、感载比例阀控制函数、流体动态时间常数和流体传动迟滞时间常数;⑦路面系统:采用高、中、低附着系数的平直路面,其中还包含路面的长度和宽度等。以某重型五轴特种车辆为例,按设计要求和参数搭建了整车动力学模型,如图10所示,部分参数如表3所示[23-24]。
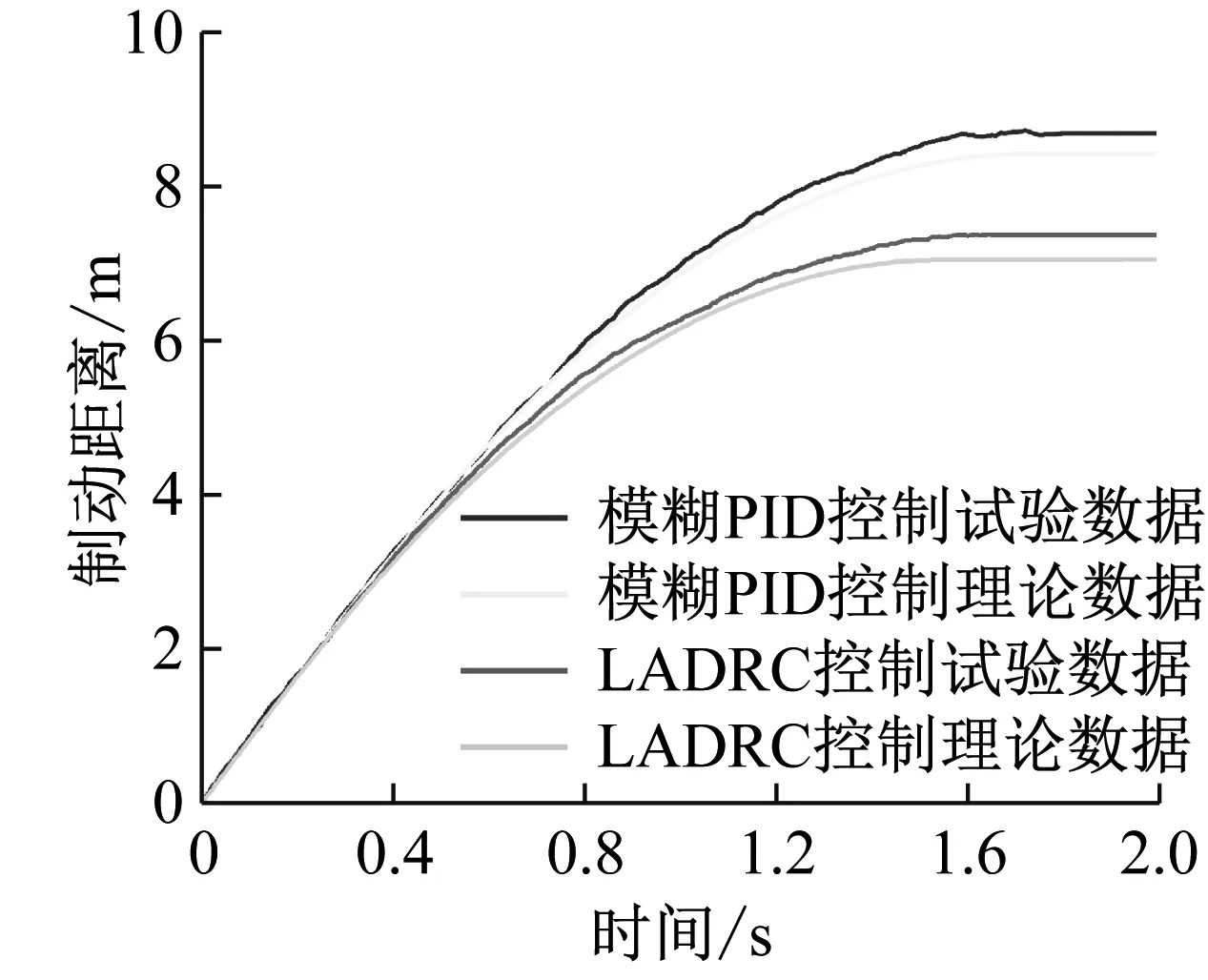
(a) 制动距离对比结果

图10 整车动力学模型Fig.10 Vehicle dynamics model

表3 整车部分参数Tab.3 Partial vehicle parameters
5 联合仿真
利用Trucksim数据通信接口,将Trucksim重型多轴特种车辆整车动力学模型与Matlab/Simulink控制系统连接起来。Trucksim整车动力学模型的输出量(车速和轮速)是Matlab/Simulink控制系统的输入量,Matlab/Simulink控制系统的输出量(制动压力)是Trucksim整车动力学模型的输入量,从而使得 Trucksim和Matlab/Simulink形成一个闭环控制。在高、中、低附着系数路面以初速度60 km/h(即16.7 m/s)进行ABS联合仿真试验。开始时间为0 s,仿真步长为0.01 s,结束时间为5 s。联合仿真模型如图11和12所示,联合仿真结果如图13所示,具体结果如表4所示。
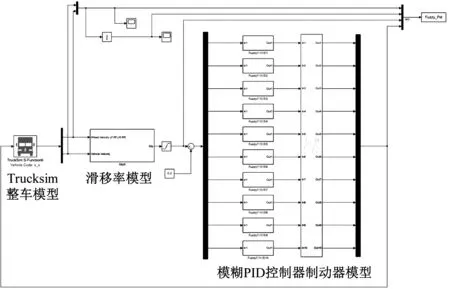
图11 模糊PID控制联合仿真模型Fig.11 Fuzzy PID control united simulation model
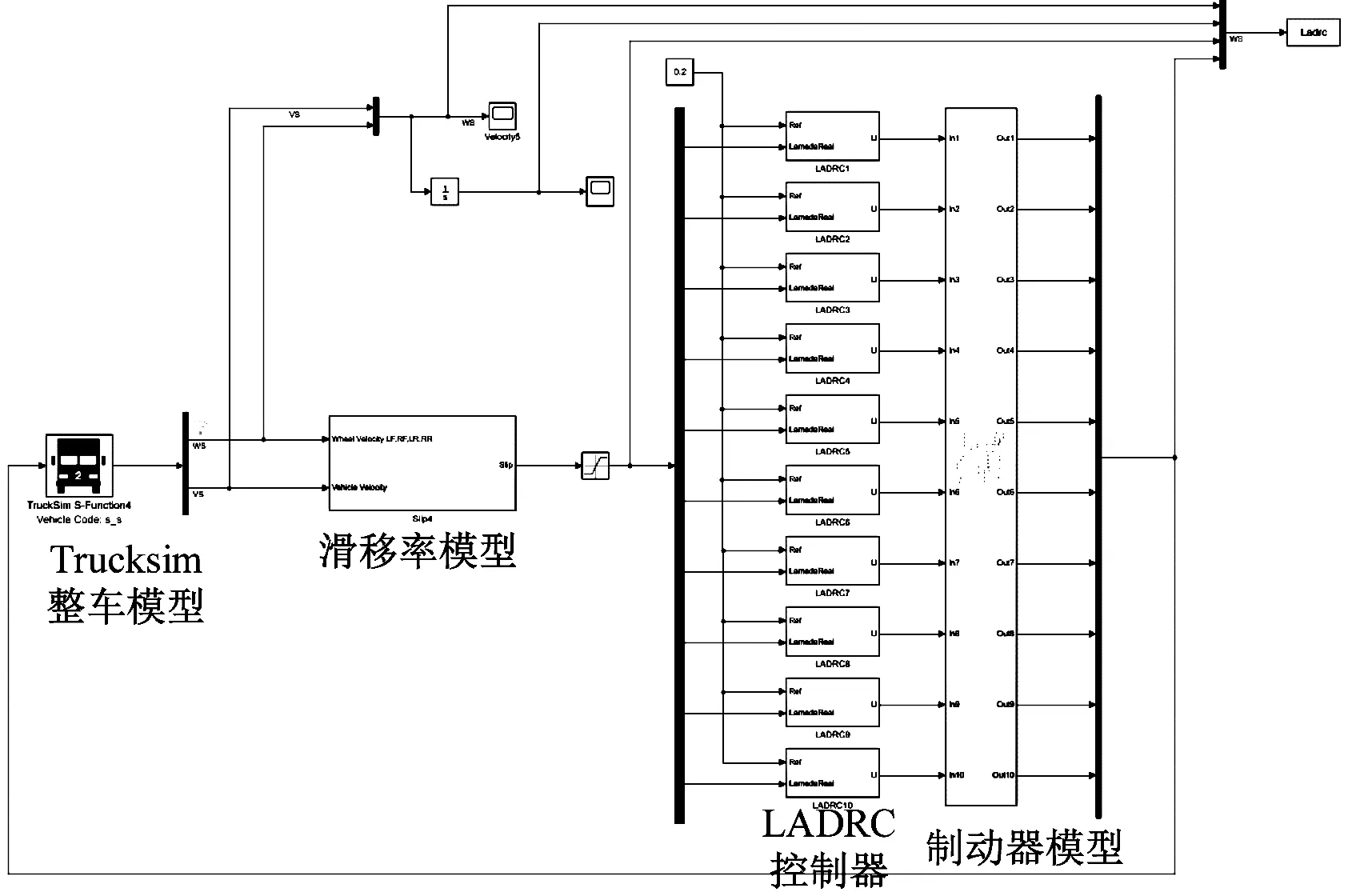
图12 LADRC控制联合仿真模型Fig.12 LADRC control united simulation model
由图13可知,在制动过程中,轮速与车速基本同步减小,未发生抱死现象,避免了车轮抱死无法转向避障,追尾碰撞和甩尾翻车等问题,但轮速的抖振现象明显,抖振程度:低附着系数>中附着系数>高附着系数;模糊PID控制>LADRC控制。
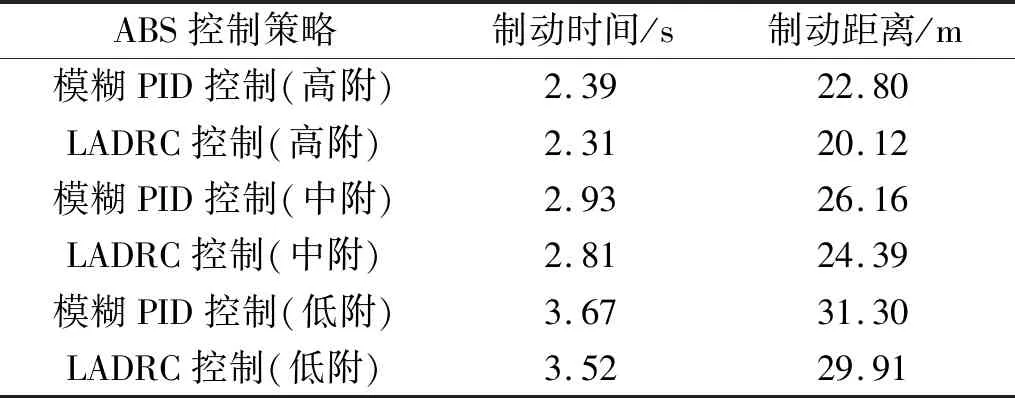
表4 仿真结果对比Tab.4 Comparison of simulation results
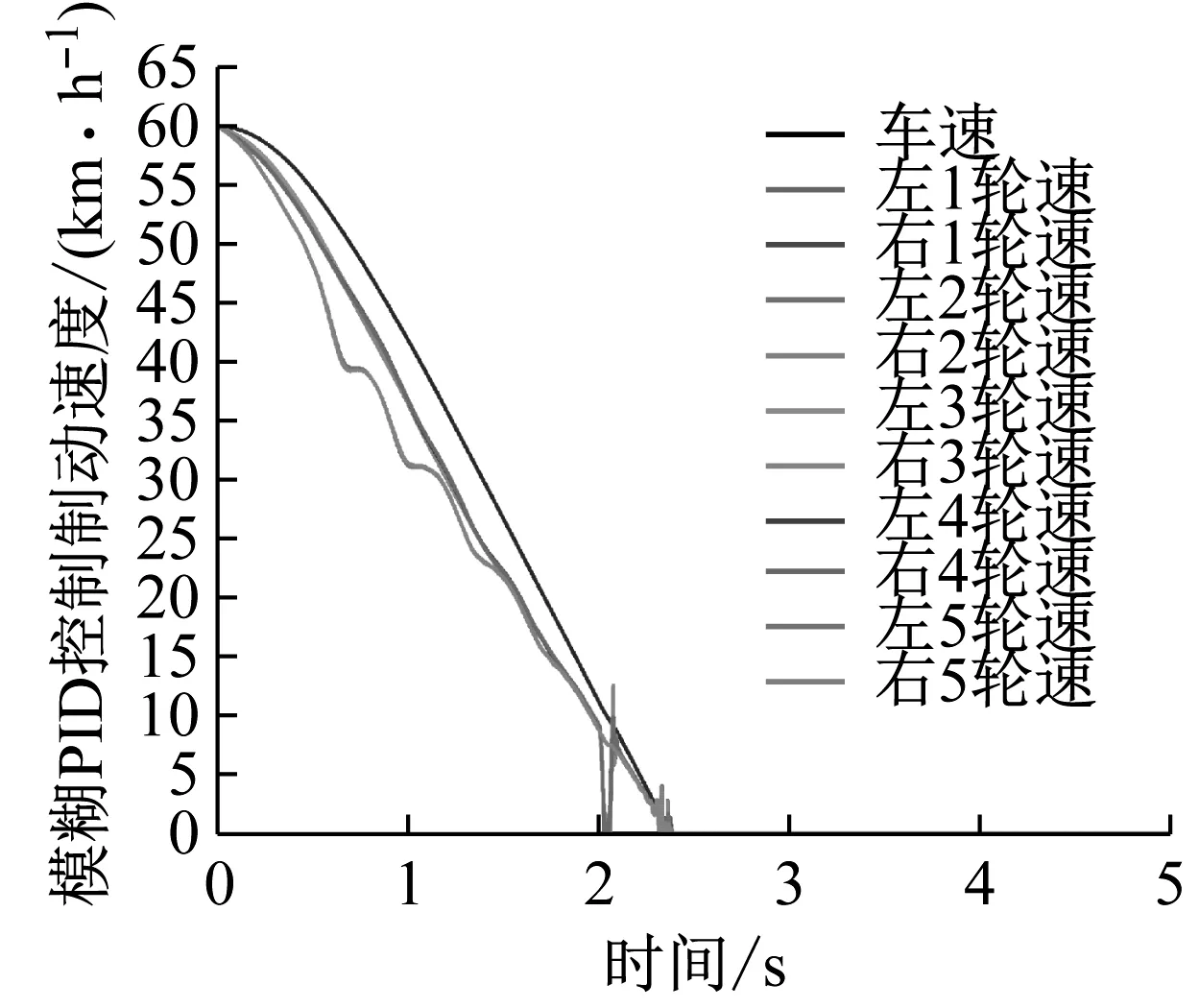
(a) 高附着系数(模糊PID)
由图14可知,在制动开始后,滑移率能够迅速达到期望值左右,但由于车身长、惯性大、轴数多,轴荷转移严重,后面滑移率有较大波动,波动幅度:低附着系数>中附着系数>高附着系数;模糊PID控制>LADRC控制;波动超调量:LADRC控制>模糊PID控制。
由图15可知,与模糊PID控制相比,在高、中、低附着系数路面,LADRC控制的制动时间分别缩短了0.08 s(3.3%)、0.12 s(4.1%)和0.18 s(4.1%),制动距离分别缩短了2.68 m(11.7%)、1.77 m(6.8%)和1.39 m(4.4%)。
分析表明:由制动时间、制动距离和滑移率的对比结果可知,LADRC控制在重型多轴特种车辆防抱死制动控制上明显优于模糊PID控制,具有更佳的制动效果。
6 结 论
本文针对传统ABS控制策略中存在的滑移率非线性、时变性和参数不确定性等问题和重型多轴特种车辆车身长、惯性大、轴数多、用途特殊以及运输环境复杂多变等特点,设计了一种基于滑移率的ABS二阶LADRC控制器,利用单轮ABS试验平台进行了对比试验,验证了LADRC控制的可行性和优越性,最后通过Trucksim和Matlab/Simulink联合仿真,应用于重型多轴特种车辆。得了出以下结论:
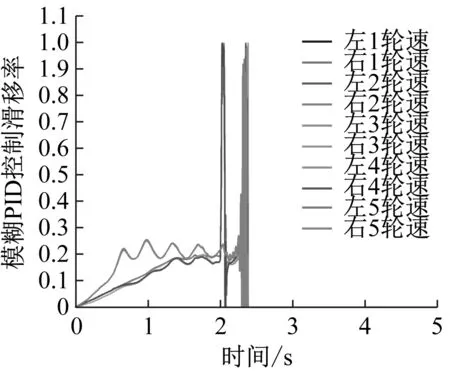
(a) 高附着系数(模糊PID)
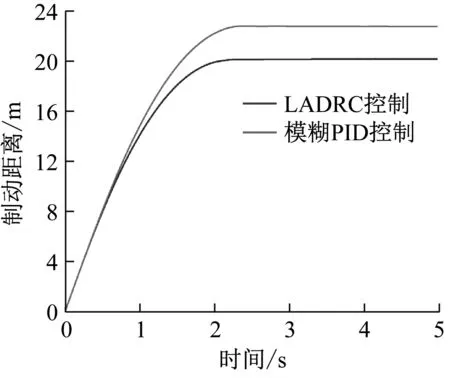
(a) 高附着系数工况
(1) 由速度波动幅度、滑移率响应时间、制动时间和制动距离可知,本文提出的LADRC控制ABS制动效果明显优于模糊PID控制,提高了重型多轴车辆的制动安全性和可靠性;
(2) 与传统ABS控制相比,ADRC控制具有不依赖于系统模型,能实时估计并补偿系统受到的各种干扰,具有更强的鲁棒性、预测性、天然的解耦性等优势,更加适合于ABS应用;
(3) LADRC与NADRC相比,不仅继承了ADRC控制的优点,而且通过将观测器极点和控制器极点分别配置在同一个位置,将繁杂的自抗扰控制器整定参数转化为仅需要整定两个带宽参数:控制器带宽和观测器带宽,从而大大简化了参数整定,便于在工程中大规模应用;
(4) 充分了发挥Trucksim在重型多轴车辆建模以及Matlab/Simulink在工程控制算法搭建上的优势,大幅削减了重型多轴特种车辆制动控制系统的开发时间和研发费用,为验证重型多轴车辆防抱死制动控制效能提供了试验平台。
附录A
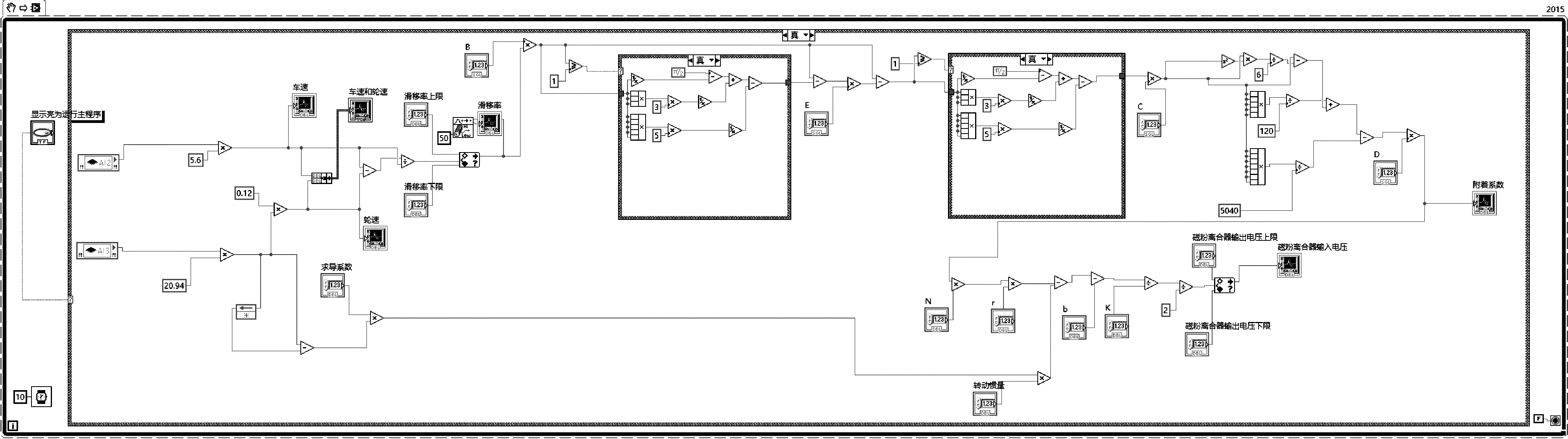
图A.1 单轮ABS实验台模型图Fig.A.1 Model diagram of single wheel ABS test bench
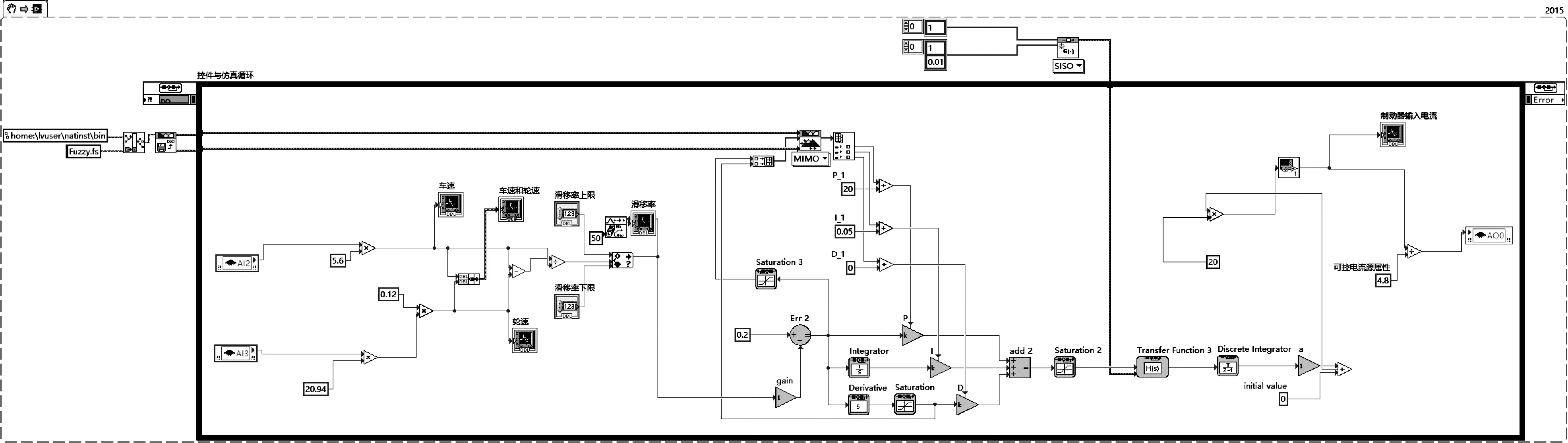
图A.2 模糊PID控制模型Fig.A.2 Model diagram of fuzzy PID control
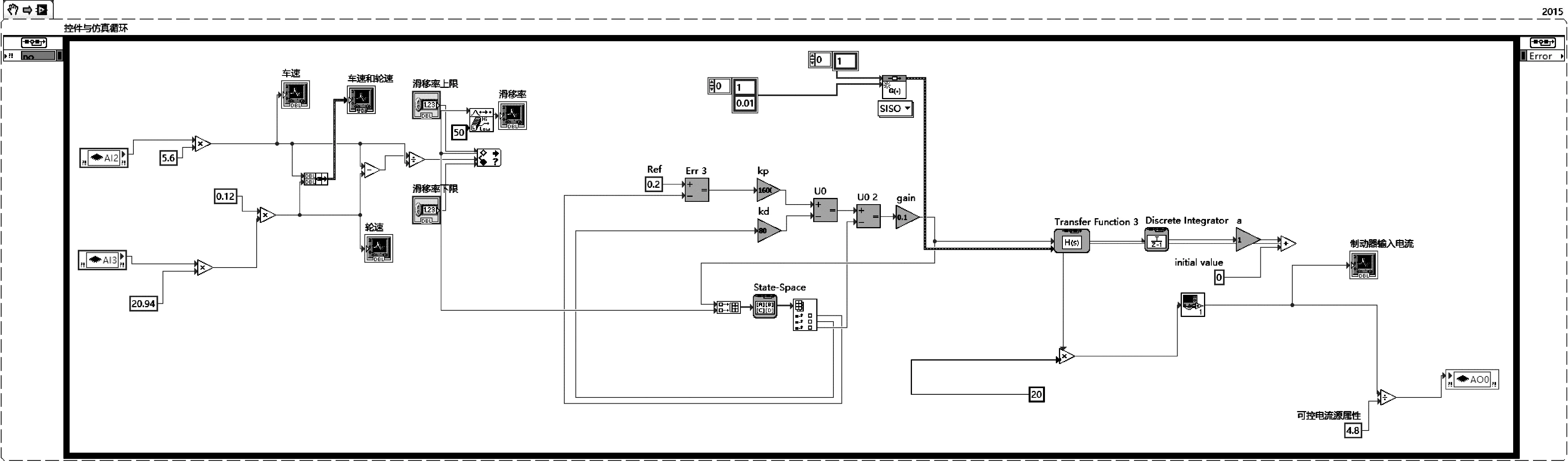
图A.3 LADRC控制器模型Fig.A.3 Model diagram of LADRC control
