具有强扰动程度的振动局域化现象研究

赵 鹏，纪 刚，周其斗

(海军工程大学 舰船与海洋学院，武汉 430033)

对周期结构的振动分析表明其在频域上交替存在通频带和止频带[1]。在通频带，振动会无衰减的传播，在止频带振动会呈现衰减趋势。当对周期结构进行某个参数的扰动后，比如子结构间距或是材料属性的不一致，结构将变为非周期系统。由于非周期系统子单元处的阻抗不再处处相同，系统会表现出完全不一样的振动传递特性，在频域上全部表现为止频带特征，振动将主要被限制在振源附近，即表现出振动局域化效应[2]。

根据结构扰动方差和单元耦合参数的相对大小，非周期结构可分为强扰动和弱扰动，强扰动则对应着弱耦合，表现出强局域化现象，其使振动在空间衰减的更快。

对非周期结构局域化效应的研究多集中在20世纪中期，一维结构方面，Bouzit等[3]通过研究单元耦合关系对多跨梁结构动力学的影响，结果表明振动局域化与单元间耦合强度密切相关，弱耦合更易导致局域化效应。同时支撑间距的随机性会导致结构振幅空间上的衰减，通过将平均变化速率表征为局部化程度，得到了局域化系数在弱跨间耦合和强跨间耦合中的解析近似。在二维系统振动局域化研究方面，Elishakoff等[4]通过研究加强筋不等间距布置对弹性板屈曲模态和振型的影响，结果发现加强筋相对标准位置的微小偏差都可以使屈曲模态从整体范围变为局部区域。Photiadis等[5]研究了无序引起壳体空间衰减变化的机理，通过针对圆柱壳不同的周向阶数进行分解实现降维，理论推导了弱扰动程度下振动衰减的近似表达式，通过分析近周期圆柱壳结构的振动响应发现，系统高阶模态有更明显的振动局域化效应。

国内对振动局域化的研究多为弱局域化效应，即分析小扰动程度下结构的动力学特征。然而实际工程中存在具有强扰动程度的非周期结构，强弱无序程度下的振动衰减系数是有很大差别的，若不加以区分，仍用弱局域化理论分析强无序结构，往往会得出错误结论。本文首先对一维弹簧振子链系统展开研究，从波传递理论角度和模态分析方法出发，结合统计扰动理论，给出对地刚度无序工况下强局域化的振动衰减系数解析式。采用基于通频带近似的等效方法，获取结构的耦合参数，近似给出环肋圆柱壳的强局域化系数。最后通过有限元数值分析验证相关结论。

1 弹簧振子链系统强局域化系数计算

振动局域化分析方法主要有摄动法、模态分析法、传递矩阵法、波传递法和数值法等[6-7]。基于研究对象的特点，采用模态分析法和波传递法定量计算典型一维结构的振动衰减系数。

如图1所示为含有对地刚度的弹簧振子链平面布置图。将系统的两端进行固支，外界激振力以幅值F，频率ω作用在左端第一个弹簧处，每个振子质量相同均为m，相互之间通过刚度系数为k的弹簧耦合，同时各自又经由刚度为ki的弹簧与大地固接。

图1 含有对地刚度的弹簧振子链系统Fig.1 Mass-spring system with ground stiffness

设第i个质量单元的位移向量表示为xi，则系统的运动方程可以表示为

-ω2mxi+(ki+2k)xi-kxi-1-kxi+1=

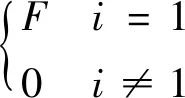
(1)

1.1 模态分析法

对于周期结构，每个子单元具有相同的物理参数，自然频率也是相同的。假设单元间耦合度为0，此时模态频率为子单元解耦频率。当耦合较小而并非消失时，模态频率将以群组的形式呈现，即表现出“模态聚集现象”，并且接近未耦合时的自然频率，这组频率就是通频带[8]。而非周期结构，各子单元自然频率不同，在频域上不存在通频带。因此对结构的无序设计，本质上是改变了系统的振动模态，模态法通过计算传递到边界处单元的单位振动响应，在整个传递距离上取平均从而分析出空间上的衰减效应。

将物理量转换为无因次形式后，系统运动方程可以改写为[9-11]

(2)

(3)

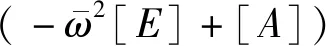
(4)

自然频率是指外力F=0时振子作自由振动的频率，式(5)表示弹簧振子链在不受外界激振力时的自由振动方程。所以通过模态分析实现行列式值的计算，系统的自然模态即转化为特征值求解问题

(5)

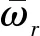
(6)

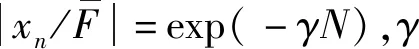
(7)

当单元数量趋于无穷多时

(8)

对于强扰动，由于无序程度很大而单元耦合强度很小，可以先将系统看成一个个对地刚度系数差别很大的独立的解耦单元，再对各单元之间赋予弹簧属性进行耦合，此时将耦合强度看作是扰动量，再利用扰动理论进行计算。

将系统运动状态矩阵[A]分解成未扰动项[A0]和扰动项[a0]

(9)

(10)

极限表达可以转换成对数函数取期望值的形式

(11)

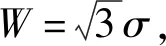
(12)

1.2 波动传递法

根据式(1)，相邻单元的运动状态方程可以转化为传递矩阵的形式

(13)

强局域化对应结构弱耦合工况，即R是小量，σ是大量，从而可以将含1/R的项看作未扰动量，其余项看作扰动量

(14)

由文献[12]可知，振动衰减系数与状态传递矩阵连续乘积的(1,1)项相关，计算得连乘矩阵的首项

(15)

最终得到表达式为

(16)

强局域化系数公式较为复杂，但也是耦合无序比值R/σ的一阶近似，适用于R/σ是小量的情况。

式(12)和(16)分别通过模态法和波传递法推导了强无序程度下的局域化系数，两种方法推导的结果相近，微小的差别是因为波传递法只取了R/σ的一阶近似，模态法推导结果含有一些高阶项。具体计算中两种数值结果相差很小，可以忽略不计。综上，系统参数R/σ的相对大小是判断非周期结构扰动强度的依据，当R/σ<1时为强扰动，反之为弱扰动。

1.3 有限元分析与数值验证

为了验证上述结论，现对一非周期弹簧振子链进行有限元分析。模型的相关参数和材料属性,如表1所示。

表1 非周期弹簧振子链模型相关参数Tab.1 Related parameters of aperiodic spring oscillator chains

现设计质量单元未扰动时的对地刚度为105n/m，扰动刚度的最大偏移量为4×104n/m，即对地刚度ki在区间(60 000,140 000)服从均匀分布，最大扰动量达40%，生成一组随机数据的无因次刚度标准差为0.232 6，耦合系数为0.1，此时σ/R>1，属于强局域化弱耦合条件。选取频率f=52、58 Hz，绘制振动能量随轴向位置的变化关系如图2(a)、(b)所示。

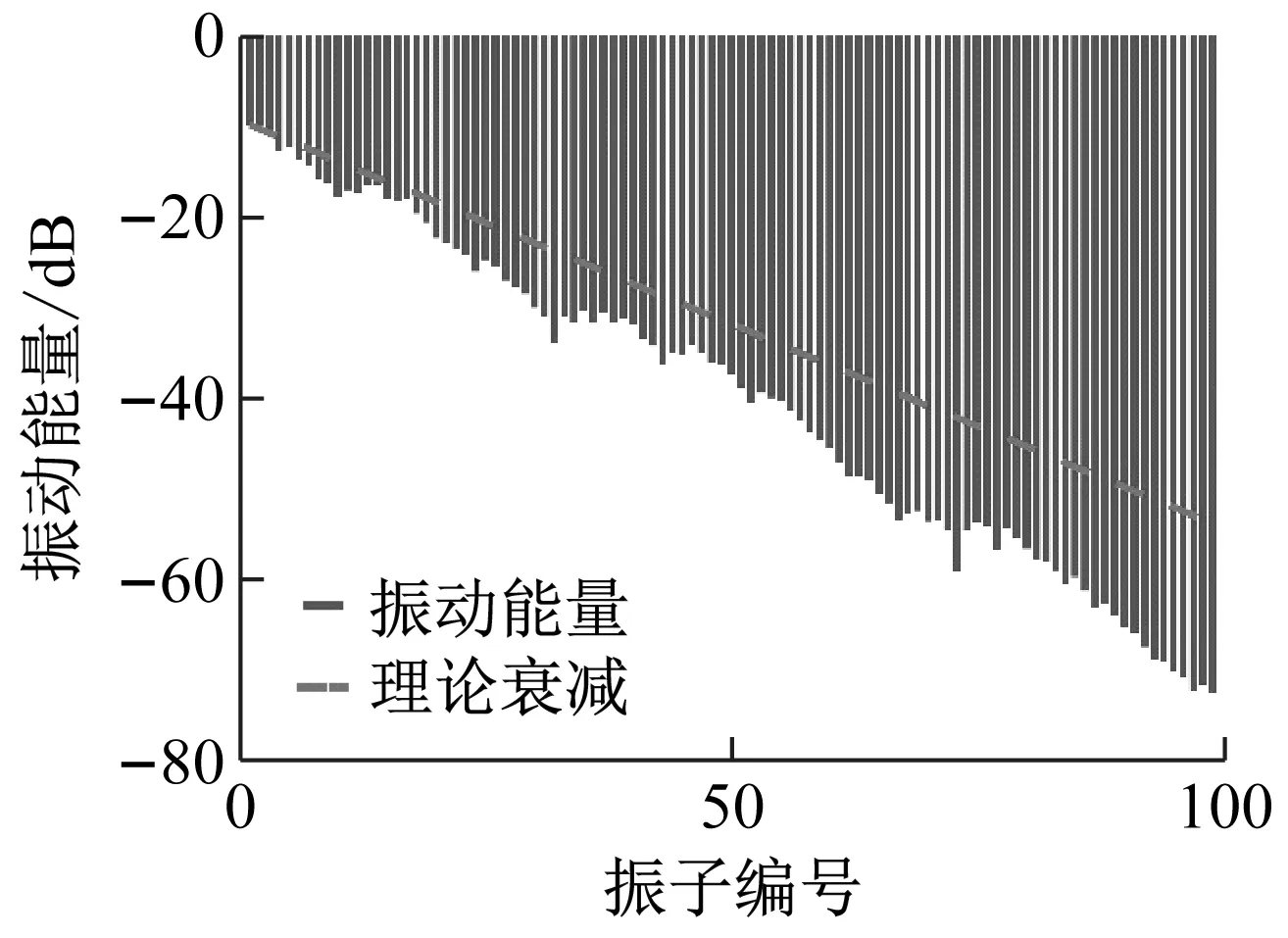
(a) f=52 Hz，强扰动

同时设计小扰动偏移量，设对地刚度在(90 000,110 000)服从均匀分布，此时σ/R<1，属于弱局域化效应，图2(c)所示为f=52 Hz下的振能图。

从图2可以看出，有限元实例模型的振幅衰减情况与强局域化系数理论结果吻合情况较好，对于强局域化弱耦合的实例模型，强局域化系数理论公式能很好地反应系统的振动衰减情况。观察图2(a)和(c)的纵坐标可以发现，扰动程度越大，局域化效应越强，振幅在空间上衰减的更快。实际分析中若忽视强局域化与弱局域化的界限，仍然采用弱局域化理论公式进行预报，将会导致相当大的偏差。

针对扰动标准差为0.232 6的上例模型，如图3所示为在频率区间(51～59)Hz通过强弱局域化理论公式计算的差异图。在中通带附近两类公式相差70%，越靠近边缘频率差异越大，在f=51 Hz处误差高达470%。

图3 两种公式计算局域化系数的差值比Fig.3 The difference between strong localization coefficient and weak coefficient

2 等效过程

首先介绍一种结构参数获取方法，理论解析二维结构的耦合参数较为困难，而根据数值解析的通频带范围可以解决这一问题，这是从一维结构过渡到二维的桥梁。下面针对弹簧振子系统验证这一方法的可靠性。

2.1 基于通频带获取结构耦合参数

对含有具体参数的周期结构进行理论计算可以给出通频带范围，同样根据通频带也能反映相关结构参数，这就是获取耦合参数的一个基本思路。对于弹簧振子系统可以通过理论计算准确地给出通频带范围，而对于板、壳等实际工程结构，由于解析复杂，很难通过理论计算识别出通频带，此时可以通过编程数值计算结构的通频带范围，从而给出用于局域化公式计算的相关参数。

对式(1)可以转化为

(-ω2mxi+kd+2k)xi-kxi-1-kxi+1=0

(17)

即：

(18)

行进波可以表示成exp(ikxx)形式，将其代入运动方程解得

(19)

其中a为振子单元间距，kx为波数，取值范围为(-π/a,π/a)。所以根据通频带的上下限频率，可以给出耦合参数k/m

(20)

如图4所示为典型弹簧振子系统的能量分布图，颜色越亮代表能量越高，从而可以清晰地确定边缘频率数值，根据通频带进一步给出子单元间的耦合刚度。

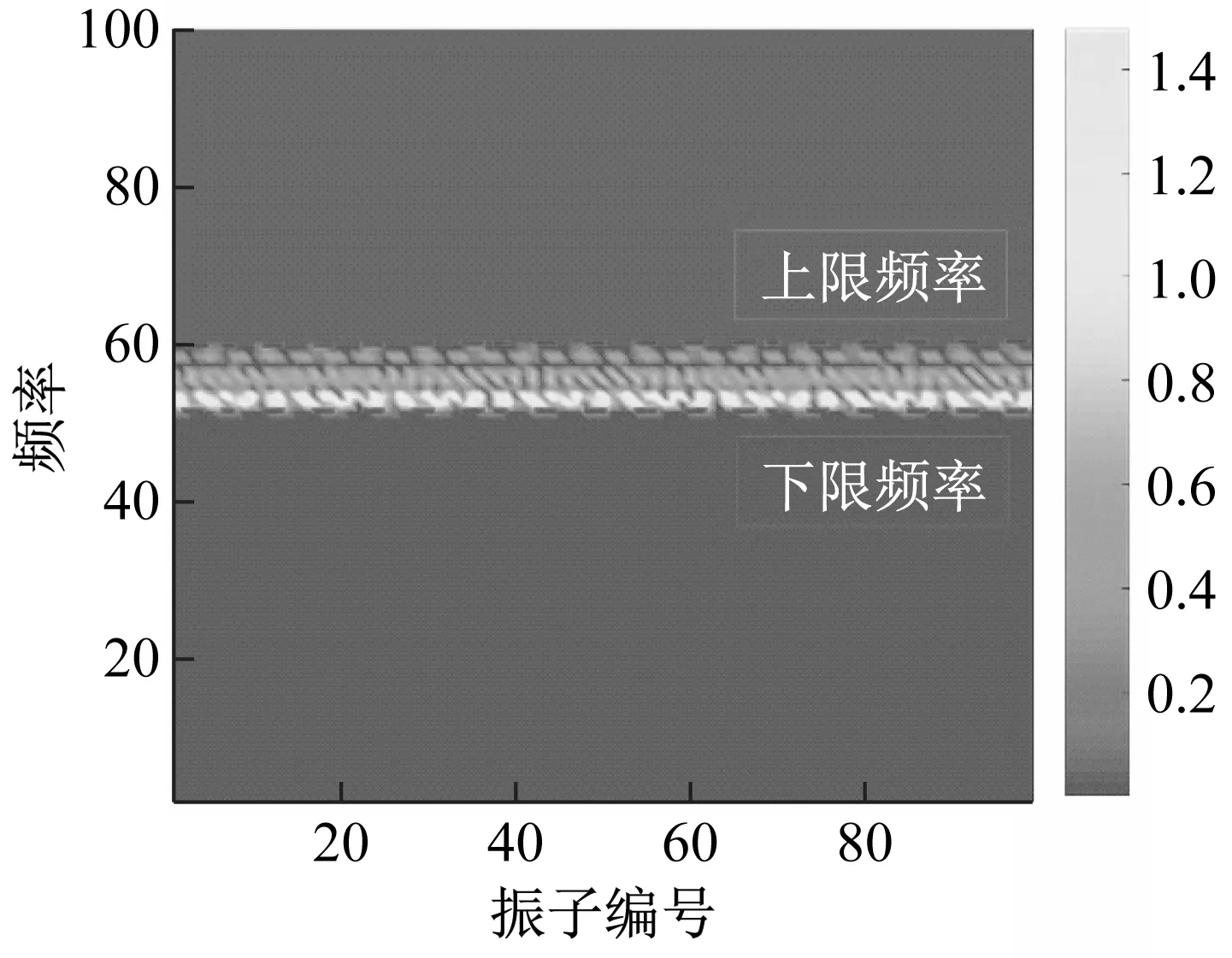
图4 弹簧振子系统能量分布图Fig.4 The energy distribution map of spring-mass system

为了验证基于通频带获取耦合参数的可靠性，现以周期弹簧振子链系统为例，根据其通带范围f=[51,59]，计算耦合参数

(21)

(22)

这就是根据通频带识别出耦合刚度后，算出特定扰动量下非周期结构的局域化系数。而根据实际参数算出各频率下的数值结果,如表2所示。

表2 特定频率下计算的局域化系数Tab.2 Localization coefficient calculated at specific frequency

对所有通频带的局域化系数取平均值为0.434 2，接近边界频率时与通过耦合参数识别计算的结果相差8.4%。这充分说明了通过能量分布图确定通频带范围，计算单元耦合参数，从而预报非周期结构的局域化系数，这一方法是切实有效的。这也为多自由度系统的局域化系数定量计算做了前提论证，通过此方法获取耦合参数具有可行性。

2.2 基于波的分解理论获取圆柱壳耦合参数

圆柱壳的振动场较为复杂，可通过傅氏级数展开理论分解为多组简单行进波的叠加，从而使分析得到简化[13-14]。对壳体进行激振，通过有限元分析得到的频响数据可分为实部项和虚部项

(23)

式中:x、θ为壳体表面的轴向和周向坐标;l为壳体轴向长度。建模过程中没有设定阻尼系数(不考虑阻尼作用)，输出各节点位移虚部均为0，所以只需对实部进行级数展开

(24)

其中：

(25)

根据各周向阶数分解后的振动幅值，可以给出n阶振动下各轴向位置的能量大小

(26)

根据式(26)绘制行进波分量的能量分布图，亮色区域为能量高值区域，可以清晰地给出通频带范围。如图5所示为某圆柱壳模型第25阶数下的能量分布图，从图可以看出二维结构具有多个通频带，可以将每个通带都等效成一维结构，从而获取结构耦合参数。

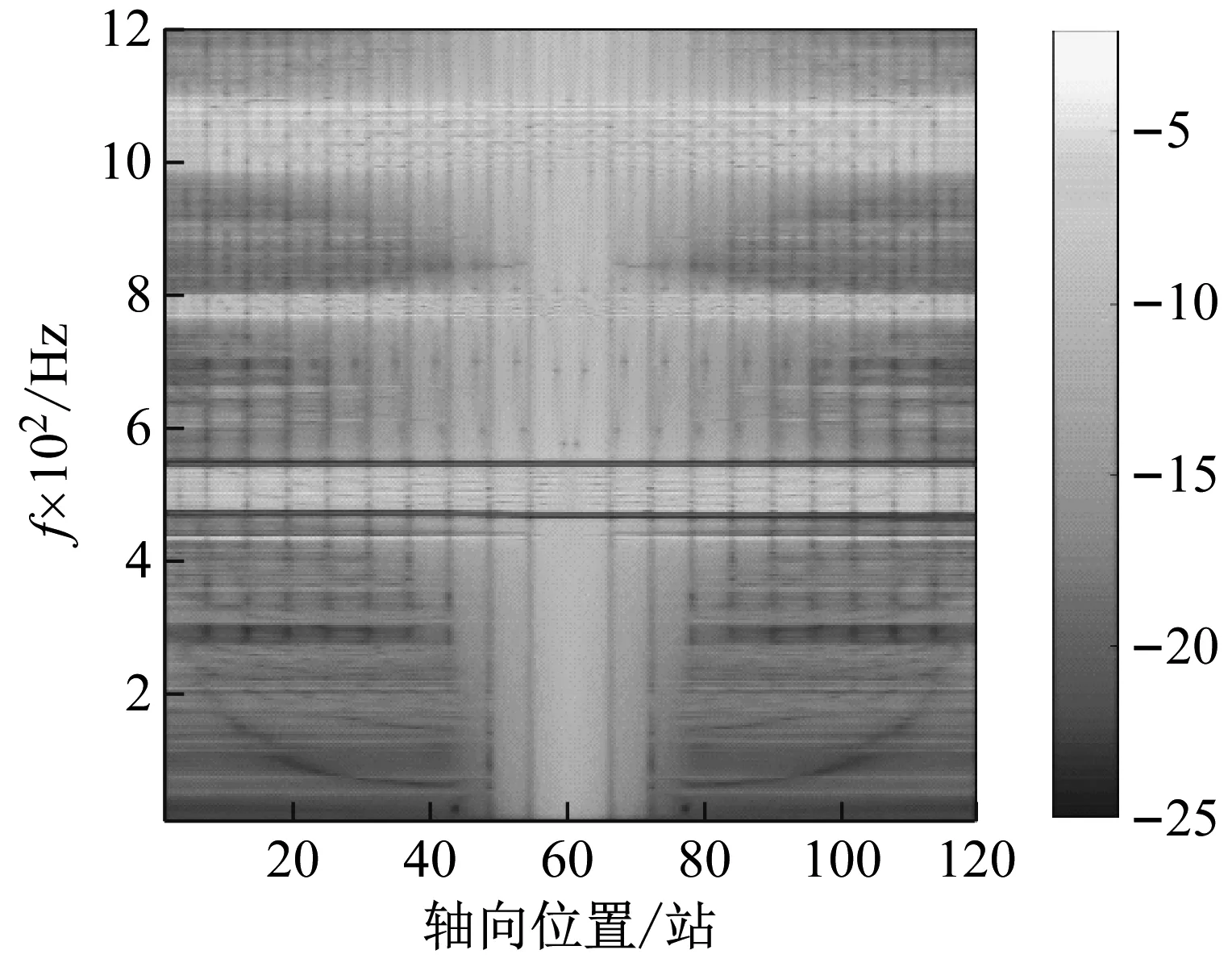
图5 圆柱壳能量分布图Fig.5 The energy distribution map of cylindrical shell

3 非周期环肋圆柱壳强局域化系数计算

基于2.1节得到壳体结构的耦合参数后，问题的关键在于推出环肋间距的扰动方差，从而可以利用一维结构的理论公式给出壳体结构的近似局域解。由文献[13]，对于非周期环肋圆柱壳，σ2表示环肋间距的无因次统计方差值

(27)

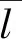
(28)

式中:n为周向阶数;R为圆柱壳半径;螺旋波波数kh可由平板色散关系式近似表达

(29)

式中:ρ为圆柱壳材料密度;ω0为通带中央角频率;E为弹性模量;ν为泊松比;h为圆柱壳板厚度。综合以上结论，环肋间距的统计方差值为

(30)

表3 环肋圆柱壳模型相关参数Tab.3 Relevant parameters of ring-ribbed cylindrical shell model

图6 有限元模型Fig.6 The finite element model

设有一激振力作用在中间环肋处，如图7所示为选取系列周向阶数和频率下振动能量随轴向位置的有限元分析与理论分析对比图。

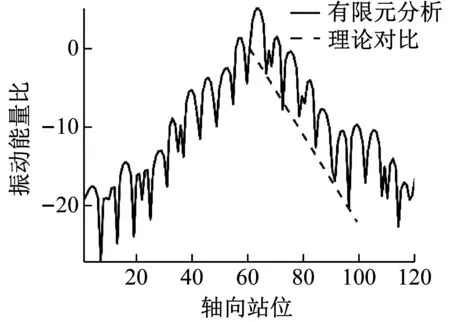
(a) n=15，f=410 Hz

从图中可以看出理论计算能较好地反映能量衰减趋势，也验证了等效方法的可靠性，实现了圆柱壳环肋间距在强扰动程度下的振动衰减预报。

4 结 论

本文首先以弹簧振子链为研究对象，研究了强扰动程度下的振动局域化现象，通过模态分析法和波传递法推导出了振动衰减系数。基于理论分析得到了基于通频带获取结构耦合参数的方法，并通过实例计算得到了验证，为圆柱壳结构的耦合参数获取打下基础。通过分析圆柱壳环肋间距的统计方差，得到了强扰动下非周期环肋圆柱壳的振动衰减系数，并通过有限元分析得到了验证。

(1) 基于模态分析法和波传递法均可推导出强扰动程度下的振动局域化系数，由于近似的阶数不同，两者有微小的差异，在数值上相当近似。

(2) 强扰动具有更大的衰减系数，在空间上表现为衰减的更快，此时若仍用弱局域化理论很可能会得出错误结论。

(3) 基于通频带可以获取结构的耦合参数，解决了圆柱壳结构系数解析复杂的难题，实现了衰减预报从一维到二维的过渡。通过计算非周期圆柱壳环肋间距的近似方差值，可以得到圆柱壳的振动衰减系数。