时变载荷激励的空调滑片式压缩机用球轴承振动特性分析

2023-02-01唐志霖蒋迪永张文虎邓四二胡余生

振动与冲击 2023年1期

唐志霖，蒋迪永，张文虎，邓四二，胡余生

(1.河南科技大学机电工程学院,河南洛阳 471000；2.杭州轴承集团有限公司，杭州 310022；3.空调设备及系统运行节能国家重点实验室，广东珠海 519000)

滚动轴承作为空调滑片式压缩机主轴的重要支承部件[1]，受到压缩机气缸腔内方向、大小周期性变化的气体力，即：时变载荷，使得其振动特性有别于恒定载荷下的轴承振动特性。因此，研究时变载荷激励的深沟球轴承振动特性，揭示影响该类轴承振动的关键因素及其振动机理对于降低空调整机振动噪音具有重要意义[2-3]。

近年来国内外学者对球轴承的振动特性进行了较为深入的研究。Shah等[4]从理论和试验两方面研究了径向载荷、波纹度阶数、波纹度幅值等参数对油润滑条件下深沟球轴承振动幅值的影响。Liu等[5]建立了含有表面波纹度和滚道局部缺陷的组合缺陷球轴承动力学模型，分析了组合缺陷尺寸对轴承径向振动的影响。邓四二等[6]建立了四列角接触球轴承的动力学分析模型，对不同结构参数与工况参数下的轴承振动特性进行了理论分析。Shah等[7]理论和试验研究了滚道表面存在局部缺陷的干接触及油润滑深沟球轴承的振动特性，研究发现：与干接触相比，润滑油膜的刚度和阻尼降低了缺陷频率下的振动速度幅值。Zhang等[8]通过大量的弹流牵引试验，研究了润滑油牵引系数对保持架非线性动力学行为的影响。研究表明：为了提高保持架稳定性，应根据高速圆柱滚子轴承的工作条件选择不同黏度的润滑油。Xu等[9]考虑滚子打滑引起的接触面磨损和不均匀的振动，从振动频率、接触应力和磨损三个方面探讨了滑动-滚动接触的振动机理。Zhang等[10]建立了乏油润滑的陶瓷球轴承非线性动力学模型，研究了含油量对轴承内圈振动的影响，结果表明：合理的含油量能够降低轴承的振动。邓四二等[11]建立了深沟球轴承的动力学仿真分析模型，对低噪音深沟球轴承结构参数、谐波参数与低噪音深沟球轴承振动特性关系进行了分析。Xu等[12]针对风力发电机组球轴承在使用过程中由于磨损而导致轴承径向游隙逐渐变大的问题，分析了游隙对轴承振动特性的影响规律。然而实际应用中滚动轴承所承受的外部载荷往往不是恒定的，变载荷下滚动体与内外圈及保持架间的动力学作用关系更为复杂。因此实际变载荷工况下的滚动轴承振动特性成为研究热点之一。Patel等[13]对健康和有缺陷的深沟球轴承在动态径向载荷作用下的振动响应进行了试验研究，但是并未建立动态载荷作用的球轴承振动分析模型。Cui等[14]提出了一种考虑时变振动载荷的球轴承疲劳损伤累积额定寿命模型。涂文兵等[15]分析了加速工况下深沟球滚动轴承滚动体动态载荷分布特性及其机理，并揭示了游隙、内圈质量和角加速度对滚动体动态载荷的影响。Zhang等[16]分析了工作条件、结构参数、材料等因素对保持架在轴承启停阶段应力分布及安全特性的影响。研究表明：在启动和停止阶段，保持架最大Von Mises 应力随着内圈加速度的增加而增加。Govardhan等[17-18]以轴承故障诊断为目标，分析了动载荷条件下圆柱滚子轴承缺陷引起的激励对轴承振动响应的影响。研究表明：由于动载荷的影响，滚动体通过频带出现了动载荷频率。Evans等[19-20]考虑轨道或车轮上的平面斑点产生的振动和冲击载荷影响，研究了非稳态条件下圆柱滚子轴承的振动特性。研究结果表明：轮轨激扰加大了滚子与保持架的作用力，加剧了轴箱轴承振动。

综上所述，目前大多数学者主要集中在研究恒定载荷下结构参数、波纹度、润滑状态、表面缺陷等因素对轴承振动特性影响。对于非稳态工况下滚动轴承振动问题的研究多为聚焦于加减速、瞬态冲击条件，尚缺少时变载荷激励的空调滑片式压缩机用球轴承振动特性分析。鉴于此，本文基于滚动轴承动力学理论，建立时变载荷激励的深沟球轴承振动分析模型，研究结构参数、工况参数对球轴承振动特性的影响。研究结果可为滑片式压缩机用球轴承的减振降噪设计提供一定的理论指导。

1 滑片式压缩机用球轴承受载分析

1.1 球轴承时变载荷激励计算

如图1所示，滑片式压缩机主要由缸体、主轴、横向凹槽、深沟球轴承及法兰组成，其中主轴由两端的深沟球轴承支承。滑片式压缩机工作原理图如图2所示，主轴在气缸内偏心配置，滑片装在主轴横向凹槽中并能沿径向自由滑动。主轴转动过程中，离心力迫使滑片紧贴在气缸壁上形成一系列月牙形横向隔室，既基元容积。压缩机工作时，各个基元容积大小随主轴转角发生周期性变化，从而产生作用于主轴的大小和方向周期性变化的气体合力。

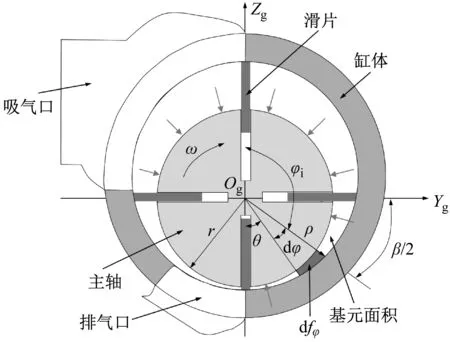
图2 A-A剖视：滑片式压缩机工作原理图Fig.2 A-A cross-sectional view:working principle diagram of vane compressor

由于压缩机气缸内产生的气体力直接由主轴两端的球轴承承载，因此首先对单个基元容积内气体压力随主轴转角变化规律进行研究，以获得轴承外载工况。作用于主轴的气体力见图2，图2中OgYgZg为建立在主轴中心的坐标系，φi为第i个基元面积的中心线与坐标轴Zg的夹角，φi代表基元面积随主轴转动的位置角。在基元面积中取一微元面积为dfφ，r为主轴半径，ρ为微元面积对应极半径长。推导出第i个基元容积内作用于主轴的气体力在Yg轴和Zg轴方向的分力为

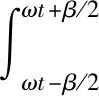
(1)

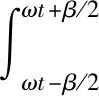
(2)

式中：Amax为φi=0时最大基元面积，pi为基元容积的吸入压力，lg为受气体力作用的主轴长度，m为多方指数，β是相邻两滑片间夹角，φi=ωt。

累加4个基元容积内沿Yg轴和Zg轴方向作用于主轴的气体力，得到作用于主轴轴承的总气体合力，表示为

Fg(t)=uFgy(t)+vFgz(t)

(3)

(4)

式中：u为Yg轴方向单位向量，v为Zg轴方向单位向量；Fgy(t)为轴承内圈在y轴方向上承受的气体合力，Fgz(t)为轴承内圈在z轴方向上承受的气体合力。

1.2 时变载荷作用的深沟球轴承承载特性

图3为深沟球轴承承载特性图。图3(a)显示恒定载荷下轴承的承载区仅随滚动体通过而微弱变化。如图3 (b)所示，内圈转动过程中受到大小方向周期性变化的载荷，从而使轴承的负荷分布范围及方向呈现时变特性。故研究时变载荷激励下深沟球轴承的振动特性具有重要的工程应用及理论意义。

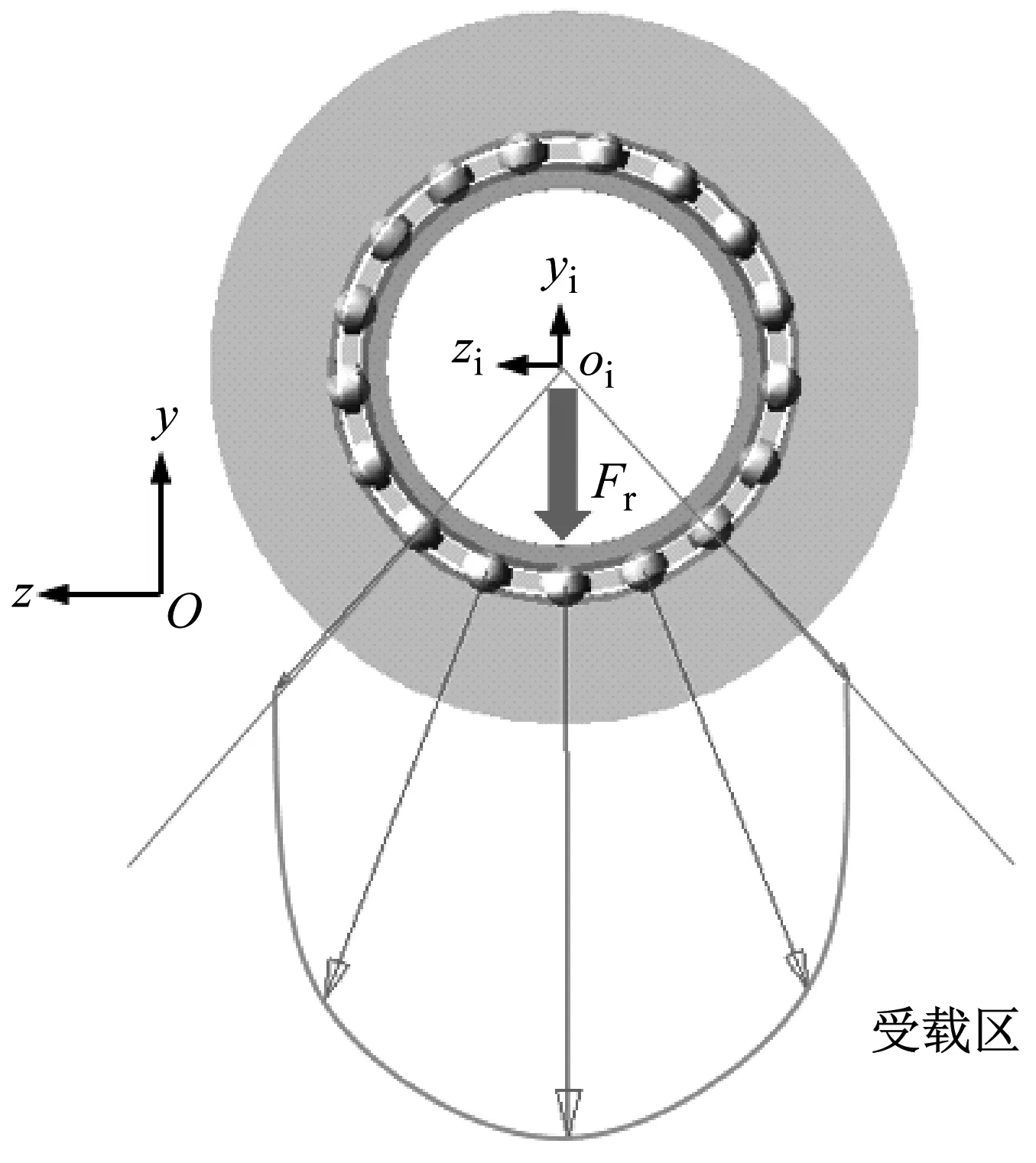
(a) 恒定载荷

2 空调滑片式压缩机用球轴承振动分析模型

2.1 深沟球轴承坐标系

建立如图4所示深沟球轴承系统坐标系描述其内部各元件的运动学及相互作用力关系。

(1) 惯性坐标系(O;X,Y,Z)。

(2) 钢球质心坐标系(ob,xb,yb,zb)，原点ob位于钢球质心，xb轴与惯性坐标系X轴平行，ybobzb平面与轴承径向平面平行。每个钢球都拥有独立的质心坐标系，并固连于钢球随其移动。

(3) 内圈质心坐标系(oi,xi,yi,zi)，原点oi与内圈质心重合，xi轴平行于惯性坐标系X轴，yioizi平面与内圈径向平面平行，坐标系固连于内圈随其移动和转动。

(4) 保持架质心坐标系(oc,xc,yc,zc)，原点oc与保持架质心重合，xc轴平行于惯性坐标系X轴，ycoczc平面与保持架径向平面平行，坐标系固连于保持架随其移动和转动。

(5) 保持架兜孔坐标系(op,xp,yp,zp)，原点op与保持架兜孔中心重合，xp轴与轴承轴线方向重合，yp轴方向始终指向轴承中心，zp轴方向沿滚动方向，该坐标系随着保持架一起运动。

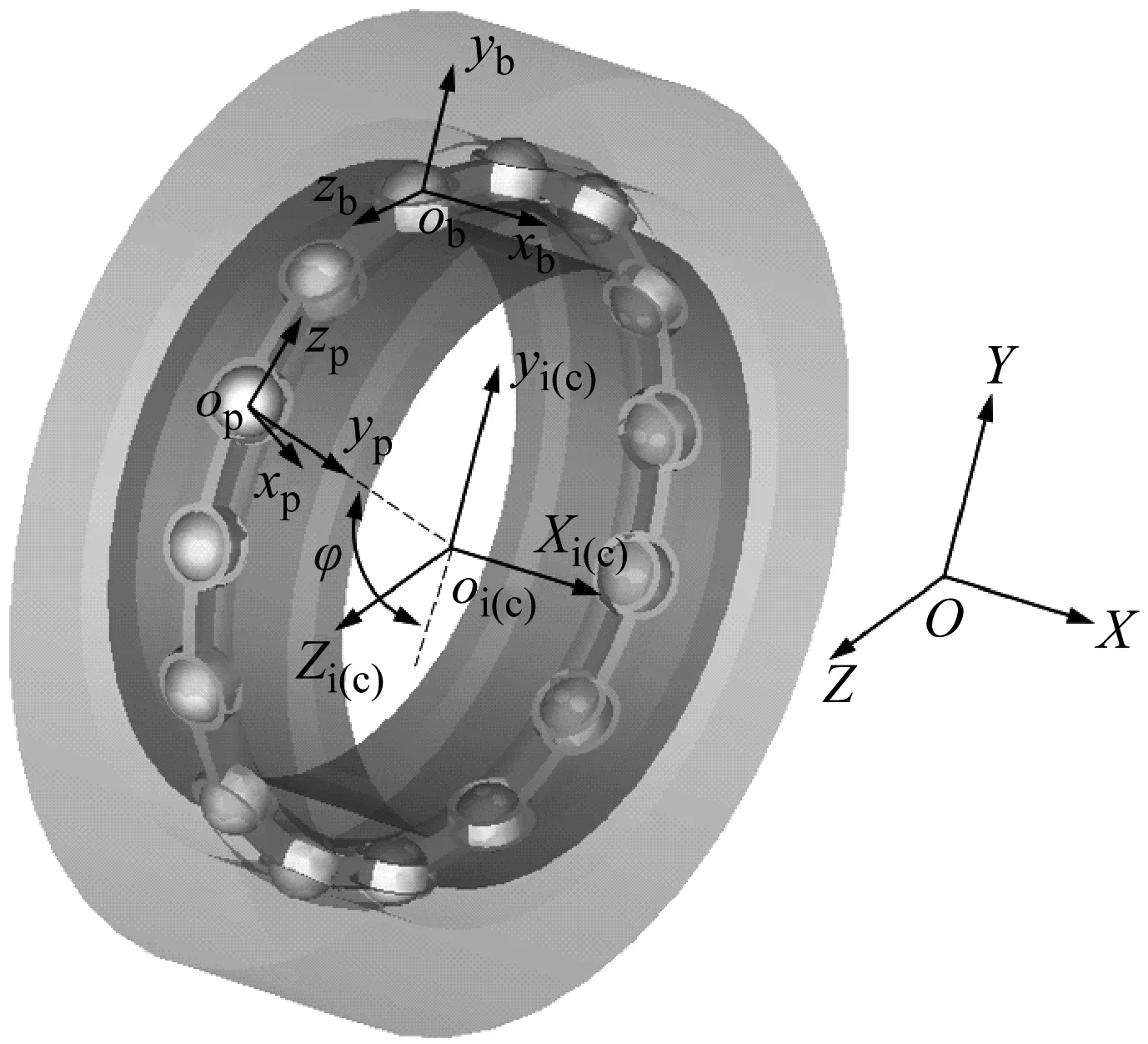
图4 深沟球轴承坐标系Fig.4 Coordinate system of deep groove ball bearing

2.2 球轴承动力学微分方程组

2.2.1 钢球动力学微分方程组

计及钢球与内外滚道和保持架兜孔间的流体动压摩擦力，钢球与内外滚道相互作用力及钢球与保持架间作用力如图5、图6所示。

图5中，下标1、2分别表示外圈、内圈；Q1j、Q2j为第j个钢球与内外滚道法向接触力；Tη1j、Tη2j、Tξ1j、Tξ2j表示钢球与滚道表面的拖动力；FRη1j、FRη2j、FRξ1j、FRξ2j为钢球与滚道接触入口区的流体动压摩擦力，FHη1j、FHη2j、FHξ1j、FHξ2j为作用于钢球中心的流体动压合力水平分量；FDj为油-气混合物对钢球产生的阻力；图6中Qcj为保持架兜孔对钢球的作用力，βyj、βzj为Qcj在兜孔坐标系下的方向角；φj为保持架兜孔坐标系在固定坐标系下的方位角；Psξj、PRξj为钢球与保持架兜孔接触面流体动压摩擦力。上述作用力计算见文献[21]。

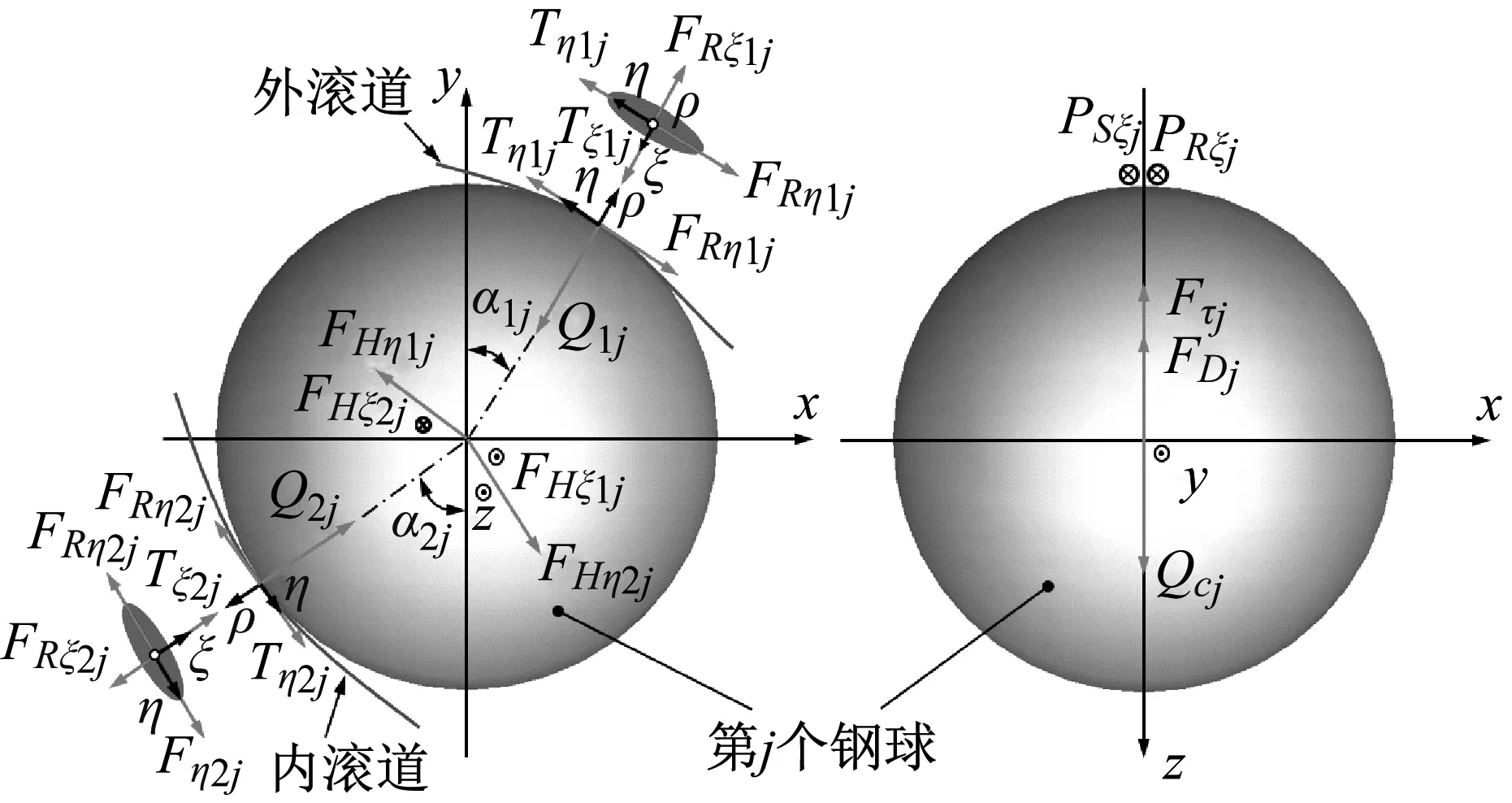
图5 钢球受力示意图Fig.5 Schematic diagram of forces on the ball

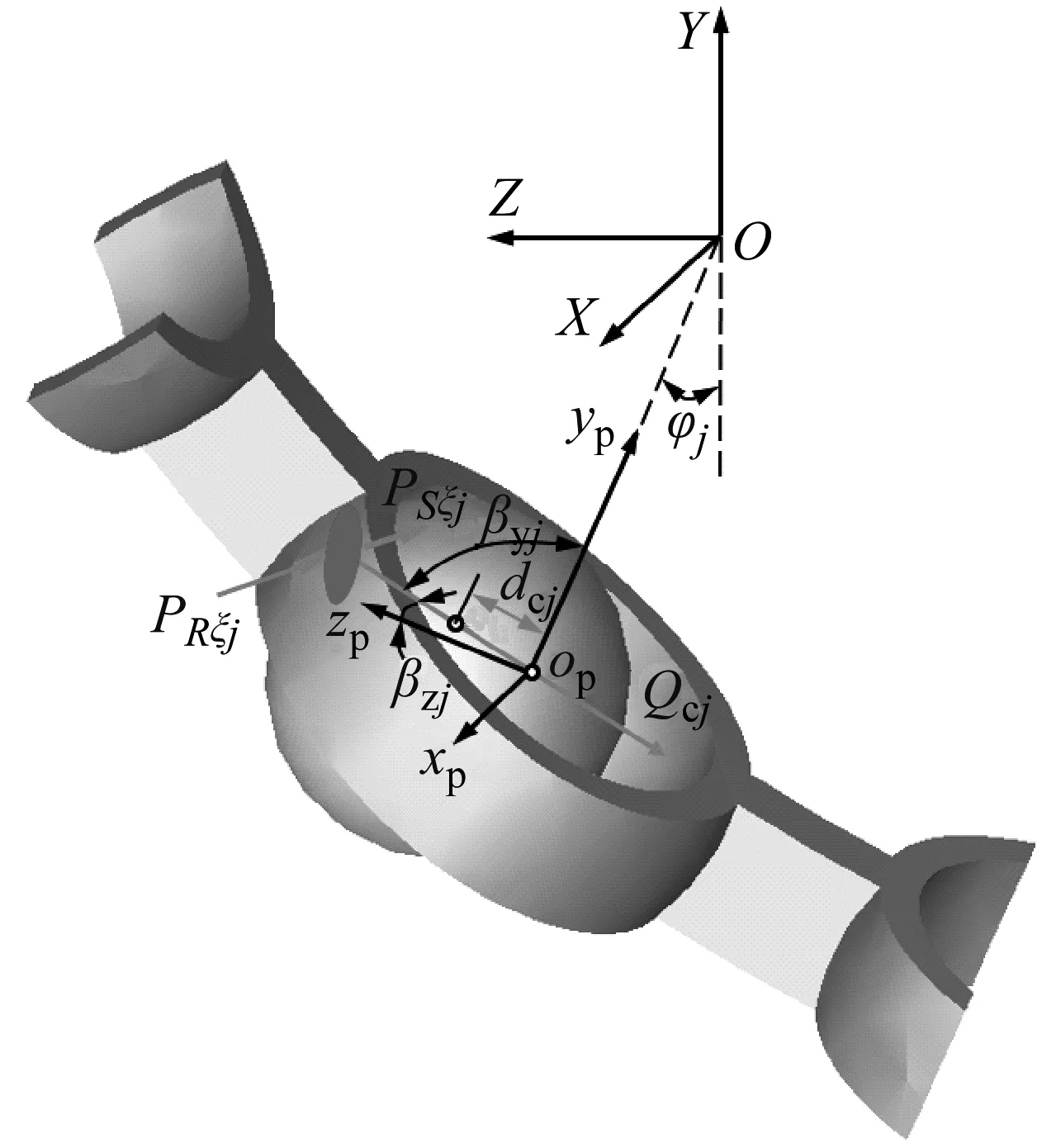
图6 钢球与保持架作用力Fig.6 Forces between ball and cage

由以上受力分析建立钢球动力学微分方程组：

(5)

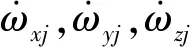
2.2.2 保持架动力学微分方程组

如图6所示，保持架为球引导，在工作过程中受到钢球的作用力。建立保持架动力学微分方程组为

(6)

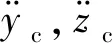
2.2.3 内圈动力学微分方程

根据内圈受力建立时变载荷激励的内圈动力学微分方程组

(7)

3 试验验证

针对在时变载荷条件下工作的球轴承，利用Miner线性损伤累积理论将时变载荷等效处理，对本文所建立的模型加以试验验证。等效载荷计算公式如下

(8)

式中：Pt为时变载荷函数；T代表变载荷周期。

采用如图7所示BVT-8型轴承振动速度测量仪(有效测量频段50～10 000 Hz、测速范围0～10 000 μm/s、仪表示值精度1 μm/s)，在轴承工作温度为20 ℃、等效径向载荷为1 060 N时，进行不同转速条件下球轴承振动试验。将试验结果与仿真结果进行对比，验证本文所建立模型的准确性。试验所用深沟球轴承主要结构参数见表1，不同转速下轴承振动频谱图如图8所示，振动速度结果对比见表2。

由图8可知，仿真模型振动速度频率主要为fbp及其倍频，试验测试得到得振动速度频率主要为钢球自转频率fbc、fbp及倍频，仿真计算得到的振动频率fbp与试验频率具有良好的一致性。由于试验轴承每个钢球的直径不可能完全一样，因此在试验测得球轴承振动信号频谱图中，含有钢球的自转频率fbc。

图7 BVT-8型轴承振动速度测量仪Fig.7 Bearing vibration velocity measuring instrument BVT-8

表1 深沟球轴承主要结构参数Tab.1 Main structural parameters of deep groove ball bearing

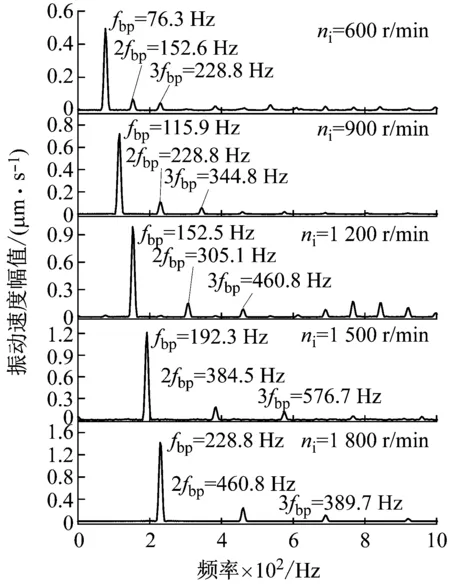
(a) 仿真结果

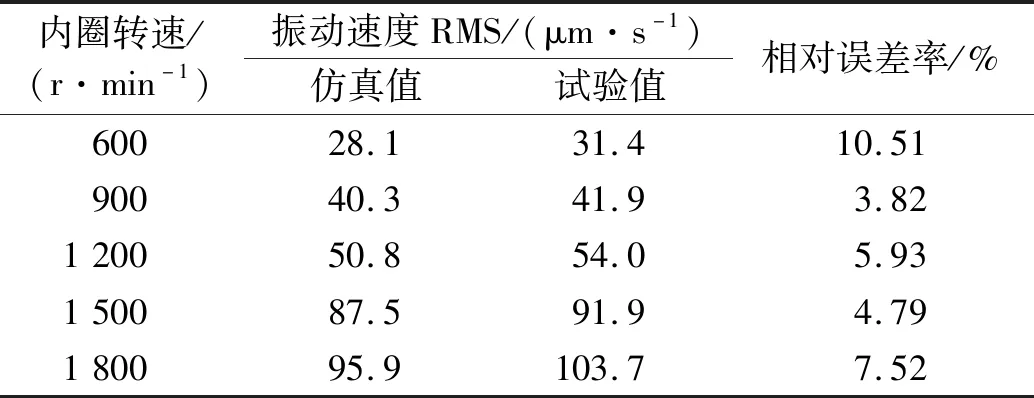
表2 振动速度结果对比Tab.2 Comparison of vibration velocity results

表2显示，仿真与试验得出的不同转速下轴承振动速度RMS值较为吻合，相对误差不超过15%，结果表明本文建立的动力学模型能较正确地分析空调滑片式压缩机用球轴承的振动特性。

4 振动特性分析

4.1 时变载荷激励的球轴承振动响应特征

运用预估与校正的GSTIFF(Gear Stiff)变步长积分算法[22]对建立的深沟球轴承动力学微分方程组(5)～(7)进行求解。轴承主要结构参数见表1，内外圈所用材料为GCr15SiMn，钢球材料为GCr15，保持架材料为SPCC，轴承润滑油牌号为68EP。为表述方便，首先对轴承各特征频率进行说明[23]，其中保持架转动频率fc，钢球通过频率fbp，时变载荷频率fFt，钢球自转频率fbc分别为

(9)

式中，ωF取决于轴承内圈的转角和转速。

如图9所示在恒定载荷下钢球与内圈接触力较为平滑不存；但在时变载荷作用的球轴承动力学模型中，钢球与内外圈接触力表现出突变性与冲击性。

图9 钢球与内圈接触力对比图Fig.9 Comparison of contact force between the ball and inner ring

为对比分析时变载荷作用的球轴承振动响应特征，分别求解了恒定载荷及时变载荷作用下轴承内圈振动速度响应，其中恒定载荷下轴承振动速度响应求解采用文献[11]模型。图10～图13给出了受恒定载荷及时变载载荷下轴承内圈在时域及频域上的振动速度响应。

由图10、图12可见，在恒定载荷作用下轴承振动频率以钢球通过频(fbp=255.68 Hz)及其倍频为主。分析图11、图13可知，实际变载作用下轴承振动响应频率取决于时变载荷频率fFt及其倍频，表现出明显的冲击性及谐波性。其低频振动冲击能量(0～1 kHz)大幅提高，在变载荷基频处振动幅值最大，中高频段内轴承振动受时变载荷的作用影响较小。

图10 恒定载荷下内圈各个频段振动速度时域图Fig.10 Time domain diagram of vibration velocity of inner ring in various frequency bands under constant load

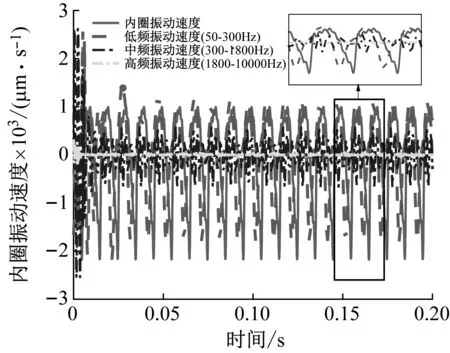
图11 时变载荷下内圈各个频段振动速度时域图Fig.11 Time domain diagram of vibration velocity of inner ring in various frequency bands under time-varying load

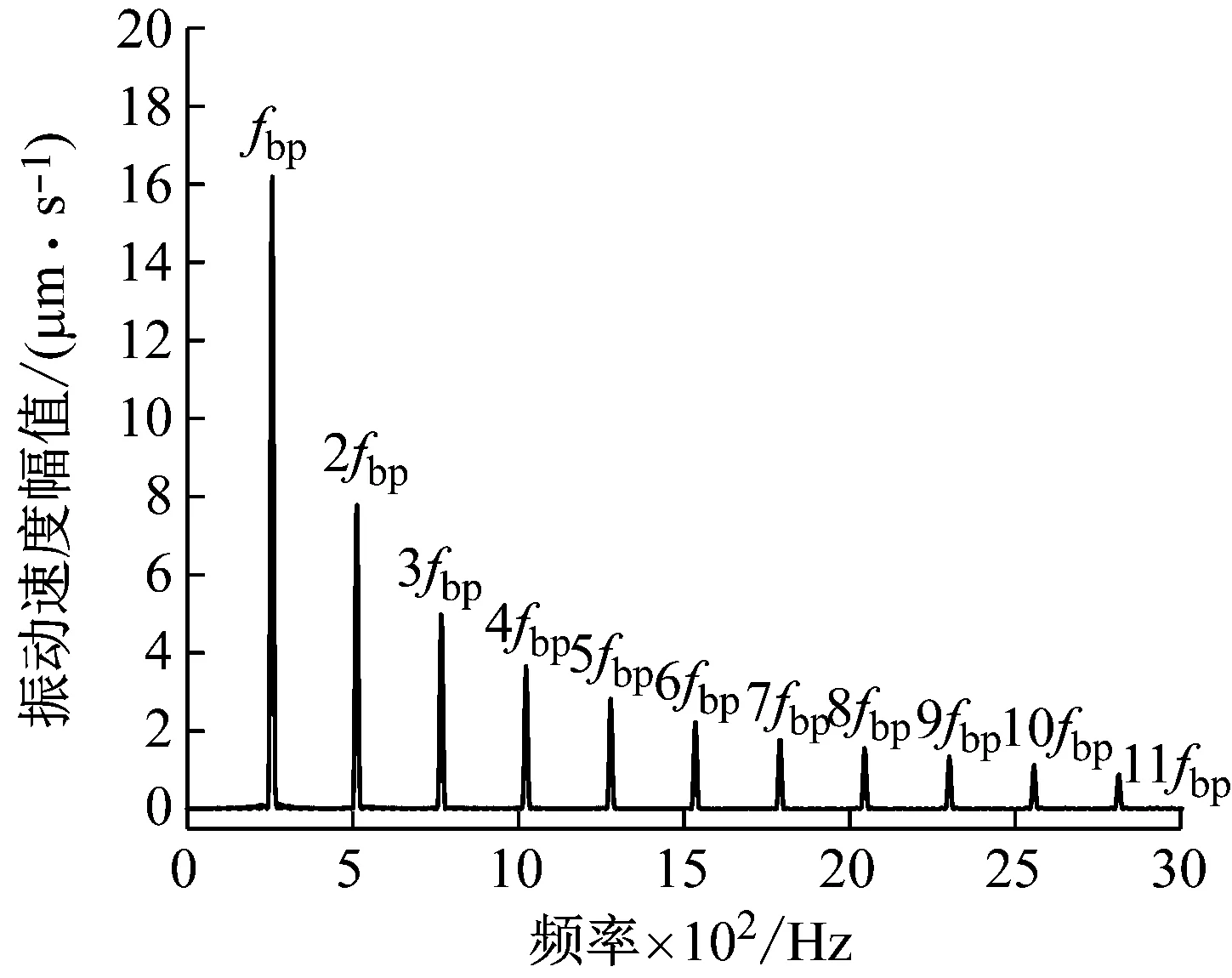
图12 恒定载荷下内圈振动速度频谱Fig.12 Vibration velocity spectrum of inner ring under constant load

特别地，图13的放大图显示，由于受到时变载荷影响,频谱出现了fbp和fFt的组合叠加频率。因此对于在时变载荷条件下工作的球轴承，本模型数值计算结果符合空调滑片式压缩机用球轴承的振动特征。

由以上分析，时变载荷作用下轴承的振动频率为中低频，根据深沟球轴承振动(速度)技术条件[24]以轴承内圈振动速度RMS(均方根)值对轴承振动进行评定。本文以工况一为典型，求解内圈Y、Z两个方向振动速度的RMS值进而研究结构、工况等参数对球轴承振动特性的影响。

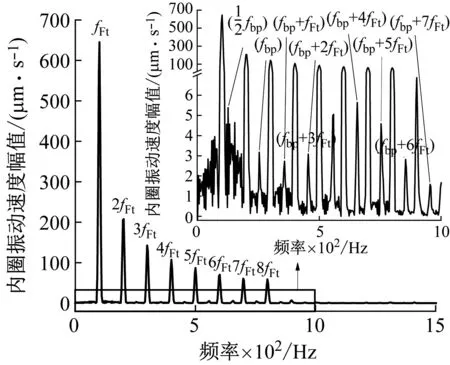
图13 时变载荷下内圈振动速度频谱Fig.13 Vibration velocity spectrum of inner ring under time-varying load

4.2 工况参数对轴承振动的影响

4.2.1 径向载荷对轴承振动的影响

在一个工作周期内压缩机产生作用到轴承内圈的气体合力如图14所示，由图可知工况3合力>工况2合力>工况1合力。

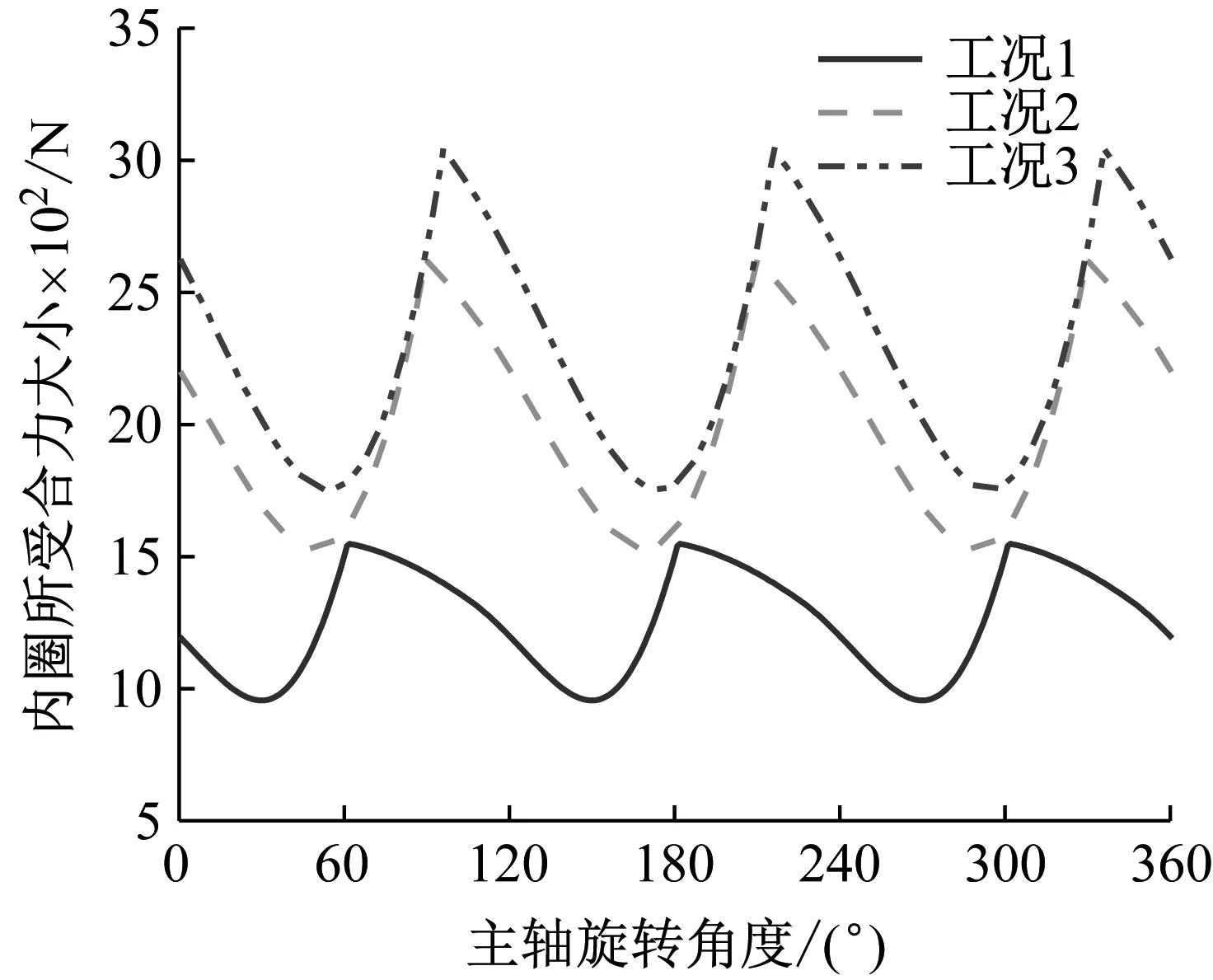
图14 轴承内圈所受气体合力Fig.14 The resultant force of gas on the inner ring of bearing

当轴承转速为2 000 r/min，原始径向游隙为0，保持架兜孔间隙为0.18 mm时，研究径向载荷对轴承振动特性的影响。图15为不同工况下内圈在Y、Z方向上的振动速度频谱图，径向载荷对轴承振动影响规律如图16。

分析图15 (a)可知，随着径向载荷的增加，fFt及其各个倍频的Y向振动速度幅值均增大；由图15 (b)可知，前6倍fFt对应的Z向振动速度幅值呈先减小后增加的趋势，而7fFt、8fFt对应的Z向振动速度幅值先增大后减小。由图16可知，随着径向载荷的增加，轴承振动速度RMS值在Y、Z方向变化规律差异较大。振动速度RMS值在Y方向上随着径向载荷载荷的增大而增加，而在Z方向上随着径向载荷载荷的增大呈先减小后增加的趋势。

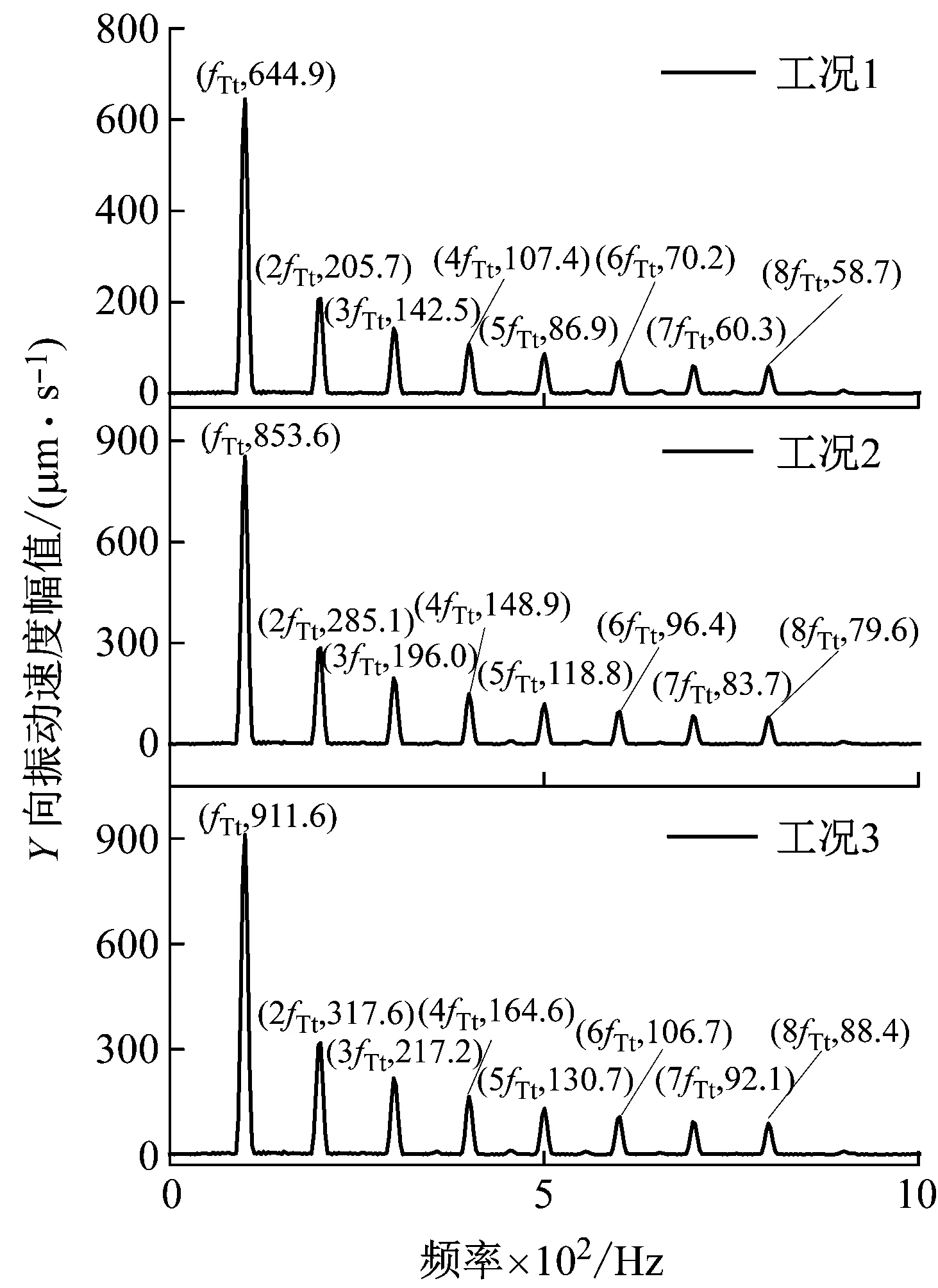
(a) Y向频谱

上述振动特性规律说明由于时变载荷作用的影响，轴承的内圈在Y、Z两个方向上的振动响应变得复杂。

4.2.2 转速对轴承振动的影响

在轴承径向受力为工况1，轴向载荷为0，原始径向游隙为0，保持架兜孔间隙为0.18 mm，内圈转速范围为1 000～5 000 r/min条件下研究转速对轴承振动特性的影响。转速为1 000～5 000 r/min对应的时变载荷频率fFt分别为50、75、100、125、150、175、200、225、250 Hz。

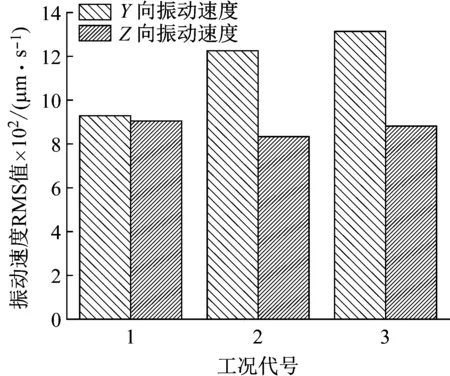
图16 径向载荷对轴承振动的影响Fig.16 Effect of radial load on bearing vibration

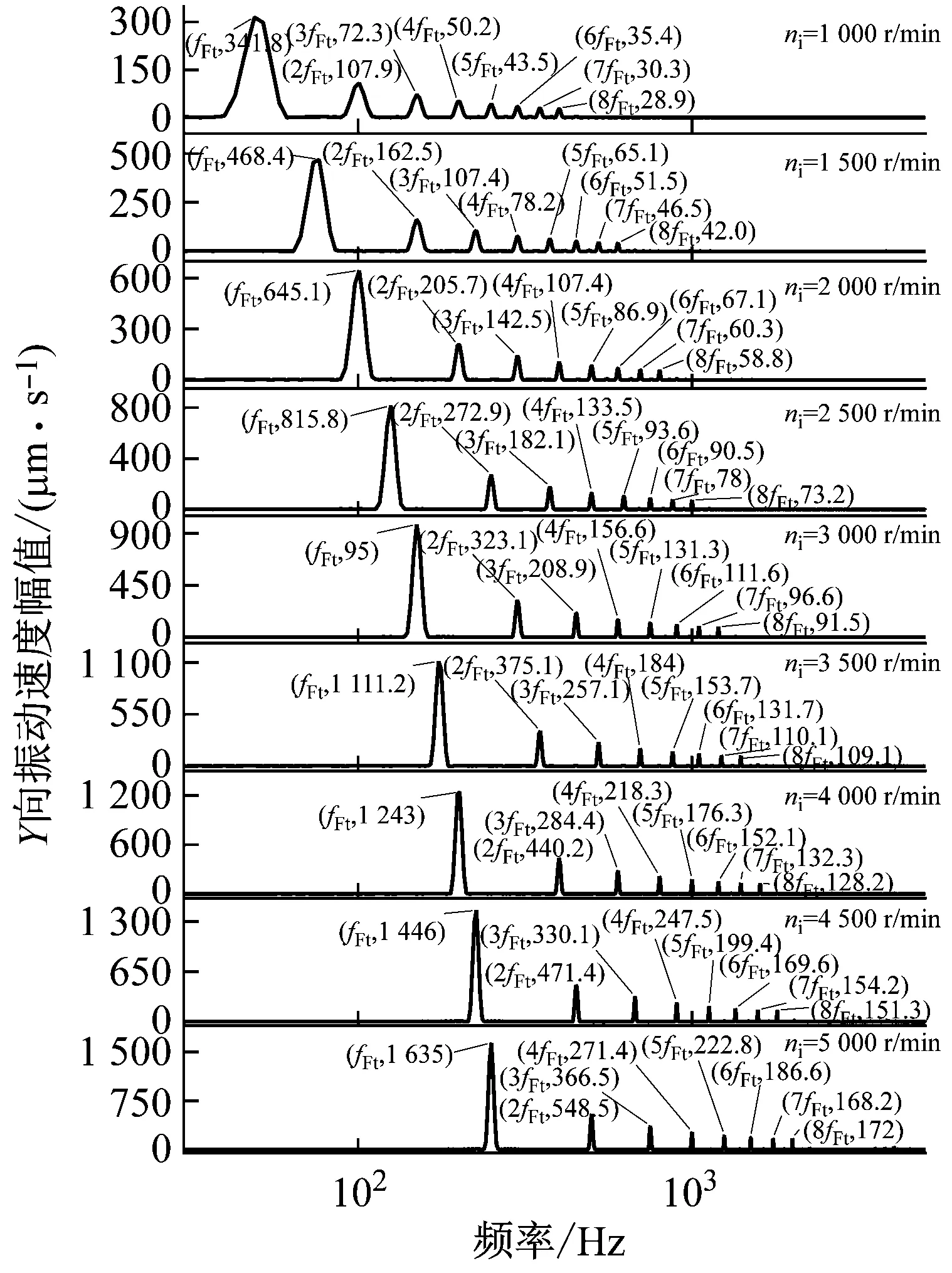
图17为不同转速下内圈振动速度频谱图，转速对轴承振动影响关系见图18。分析图17可知随着轴承转速的增加,Y、Z方向上的振动主频相应地增加，且各个倍频的振动速度幅值也增加。由图18可知，轴承Y、Z方向振动速度RMS值均随着转速的增加而增加。

分析表明：时变载荷频率fFt决定了轴承的振动的主频。随着转速的增加，轴承振动速度幅值增大，这是由于转速的增加使得变载荷对轴承振动的激励频率增加从而加大了轴承的振动能量。

4.2.3 轴向预载荷对轴承振动的影响

定义轴向预载荷因子Ca为轴向预载荷比额定动负荷。图19为不同轴向预载荷下轴承振动频谱图。图20为轴向预载荷对轴承振动速度的影响规律图。分析图19(a)可知：对深沟球轴承施加一定轴向预载荷后，1倍～6倍fFt对应的Y向振动速度幅值呈先减小后增大的趋势，7倍、8倍fFt的振动速度幅值缓慢增大。由图19(b)可知，Z向振动速度各倍频幅值随预载荷的增大而增加。如图20所示，对轴承施加一定的轴向预载荷后Y向振动速度RMS值先减小后增大，Z向振动呈增大趋势。Y、Z方向振动速度的合成即轴承径向平面振动速度RMS值呈现先减小后增大的趋势。因此建议对滑片式压缩机球轴承选用预载荷因子为0.3%～0.6%的轴向预紧力以降低轴承振动噪音。

4.2.4 钢球与滚道间摩擦因数对轴承振动的影响

在轴承径向受力为工况1，转速为2 000 r/min，原始径向游隙为0，保持架兜孔间隙为0.18 mm情况下研究钢球与滚道间摩擦因数对轴承振动特性的影响规律。

图21为不同摩擦因数下内圈振动速度频谱图，图22为钢球与滚道间摩擦因数对轴承振动的影响图。分析图21可知：摩擦因数主要对fFt对应的振动速度幅值有影响，fFt对应的Y、Z方向振动速度幅值均随摩擦因数的增大而先减小后增大。由图22可知，随着轴承摩擦因数的增大，轴承Y、Z两个方向上的振动速度RMS值先减小后快速增大。说明过大的摩擦因数会加剧轴承的振动。由于钢球与滚道间摩擦因数主要受润滑剂黏度的影响并且随润滑剂黏度的增加而增大[25-26]。因此，对于本分析型号轴承选用黏度适中的润滑剂能够使轴承在较低振动状态下工作。

(a) Y向频谱

4.3 结构参数对轴承振动的影响

当轴承径向受力为工况1，轴向载荷为0，内圈转速为2 000 r/min条件下研究结构参数对轴承振动特性的影响。

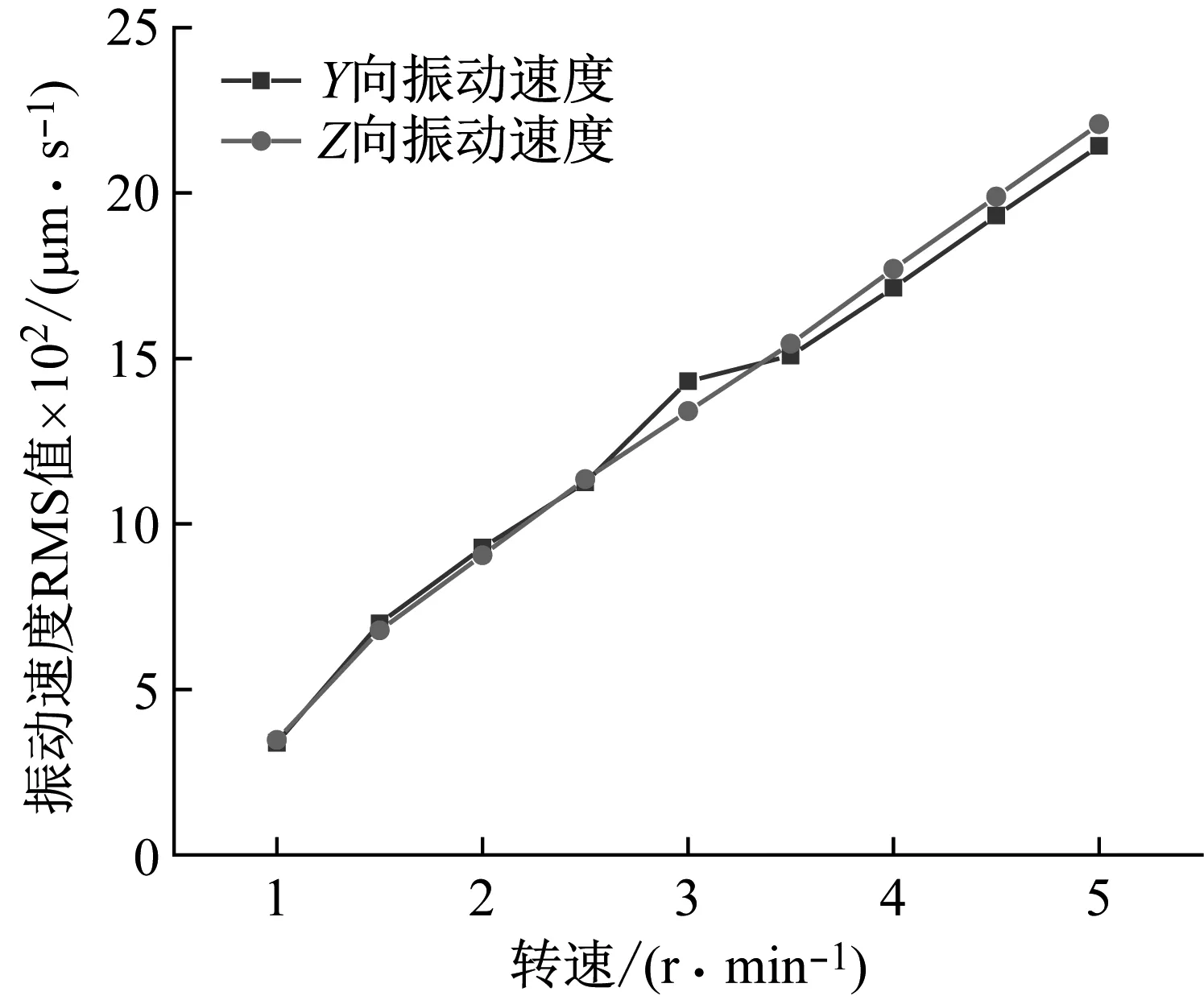
图18 转速对轴承振动的影响Fig.18 Effect of rotational speed on bearing vibration

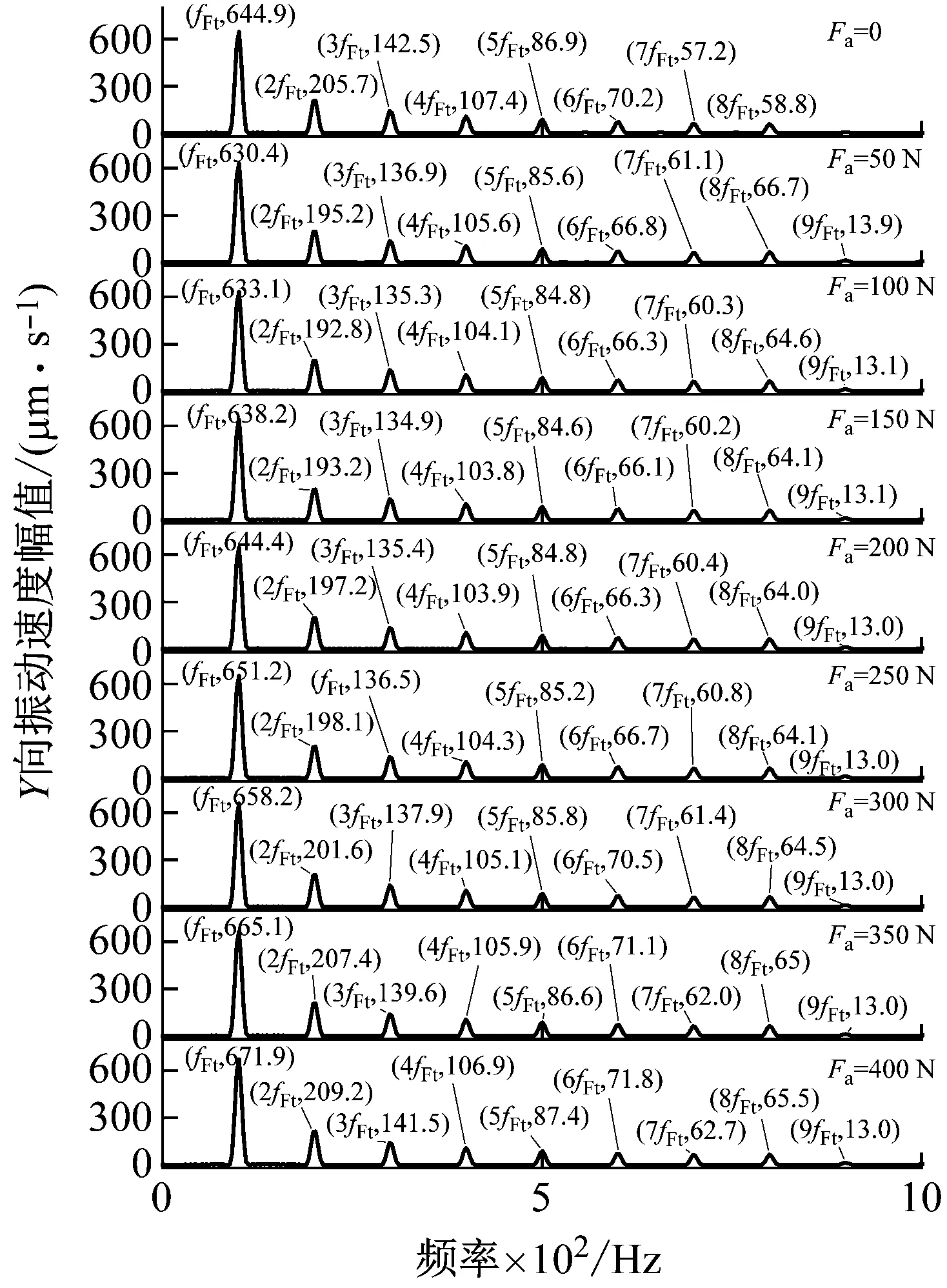
(a) Y向频谱

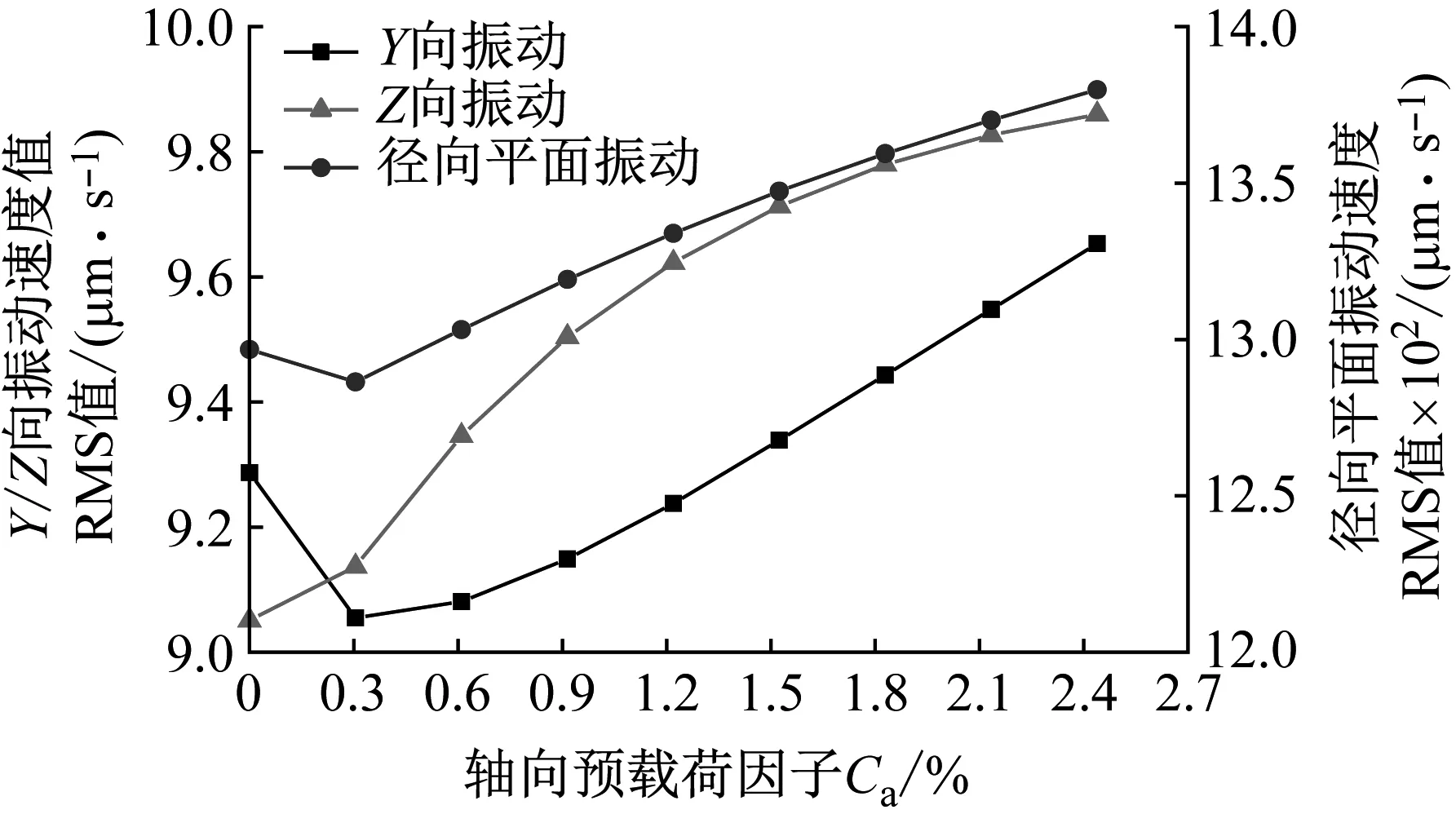
图20 轴向预载荷对轴承振动影响Fig.20 Effect of axial preload on bearing vibration

(a) Y向频谱

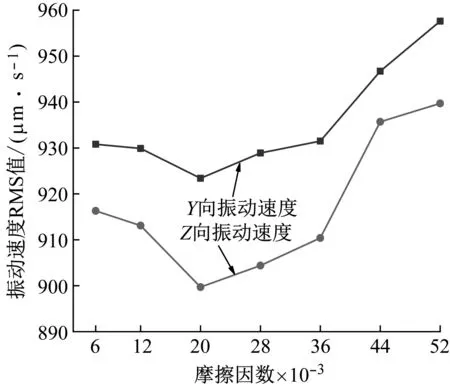
图22 钢球与滚道间摩擦因数对轴承振动的影响Fig.22 Effect of friction coefficient between ball and raceway on bearing vibration

4.3.1 原始径向游隙对轴承振动的影响

图23为不同原始径向游隙下内圈振动速度频谱图，原始径向游隙对轴承振动影响关系见图24。由图23 (a)可知当径向游隙从-10 μm增加到-6 μm的过程中，fFt及其各倍频对应的Y向振幅大幅度增加；当径向游隙由-6 μm增加到14 μm时fFt频率下的振幅呈近似线性的趋势增加，但是2fFt、3fFt频率下的振幅逐渐降低。由图23 (b)可知，随着径向游隙的增大，各倍频对应的Z向振幅均快速增加。从图24可以看出，随着径向游隙的加大，Y、Z方向的振动速度RMS值均变大且Z向振动幅值超过了Y向振动幅值。

导致上述振动特性的主要原因是：随着原始径向游隙的增大，轴承的承载区域减小，轴承内圈由于在Y轴方向受载较大所以被压往Y向一侧，从而增大了轴承在Z轴方向上的游隙。在轴承内圈受到Z方向的时变载荷激励后轴承振动加剧。由以上分析得出，过大的原始径向游隙不利于降低轴承的振动，对于本类型号轴承采用零游隙或负游隙可以有效降低时变载荷对轴承冲击的影响。

4.3.2 保持架兜孔间隙对轴承振动的影响

图25为不同保持架兜孔间隙下保持架振动速度频谱图，图26为保持架兜孔间隙对轴承内圈及保持架振动的影响规律。

由图25 (a)可知，保持架振动频率主要为保持架转动频率fc、时变载荷频率fFt及其倍频。随着兜孔间隙的增大，fc对应的保持架Y向振动速度幅值呈先减小后增大趋势，fFt及其倍频对应的振动幅值呈缓慢减小趋势。由图25 (b)可知，随着兜孔间隙的增大，fc对应的保持架Z向振动速度幅值呈先减小后增大趋势，fFt及其倍频对应的振动幅值缓慢增大。

(a) Y向频谱

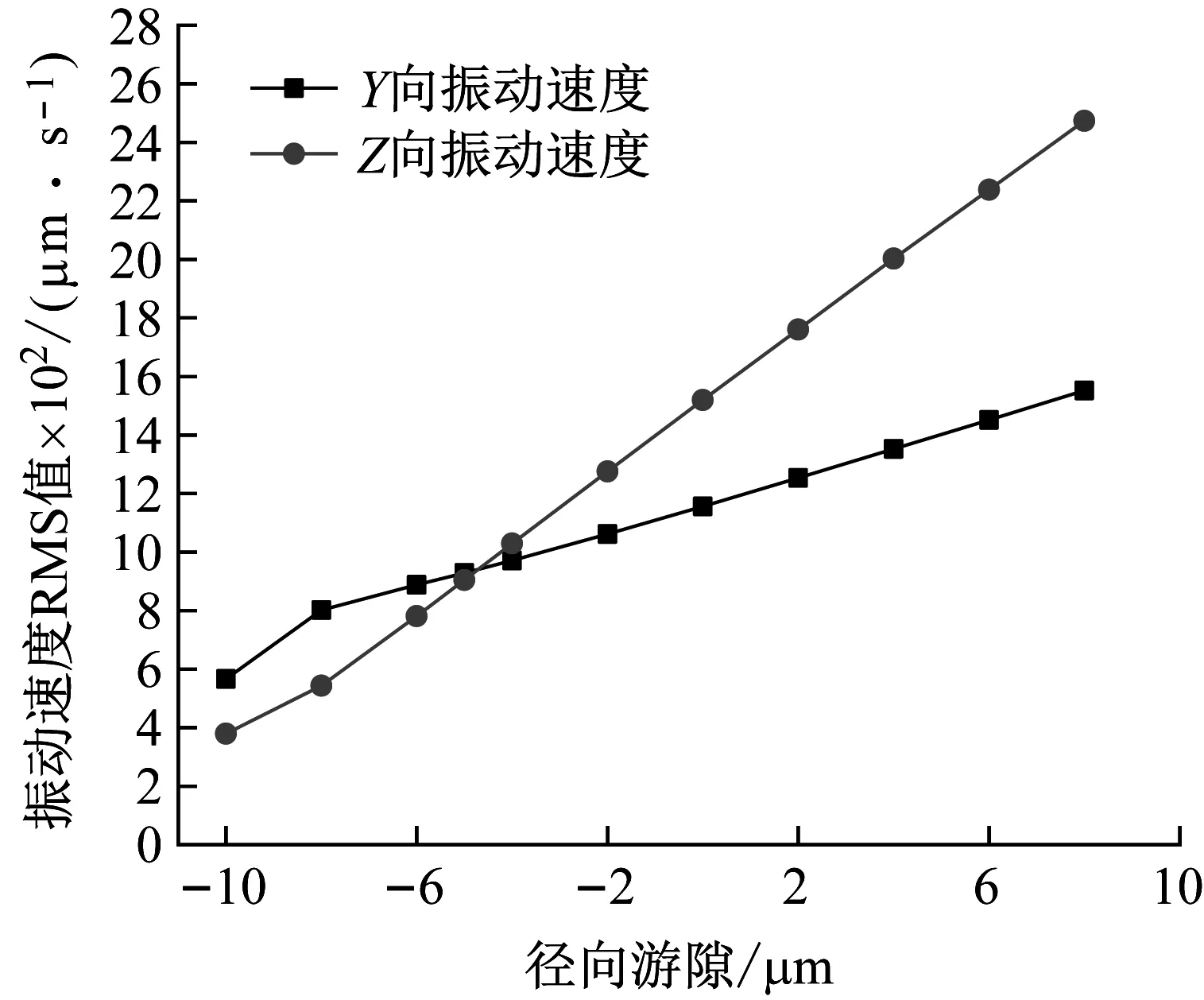
图24 原始径向游隙对轴承振动的影响Fig.24 Effect of original radial clearance on bearing vibration

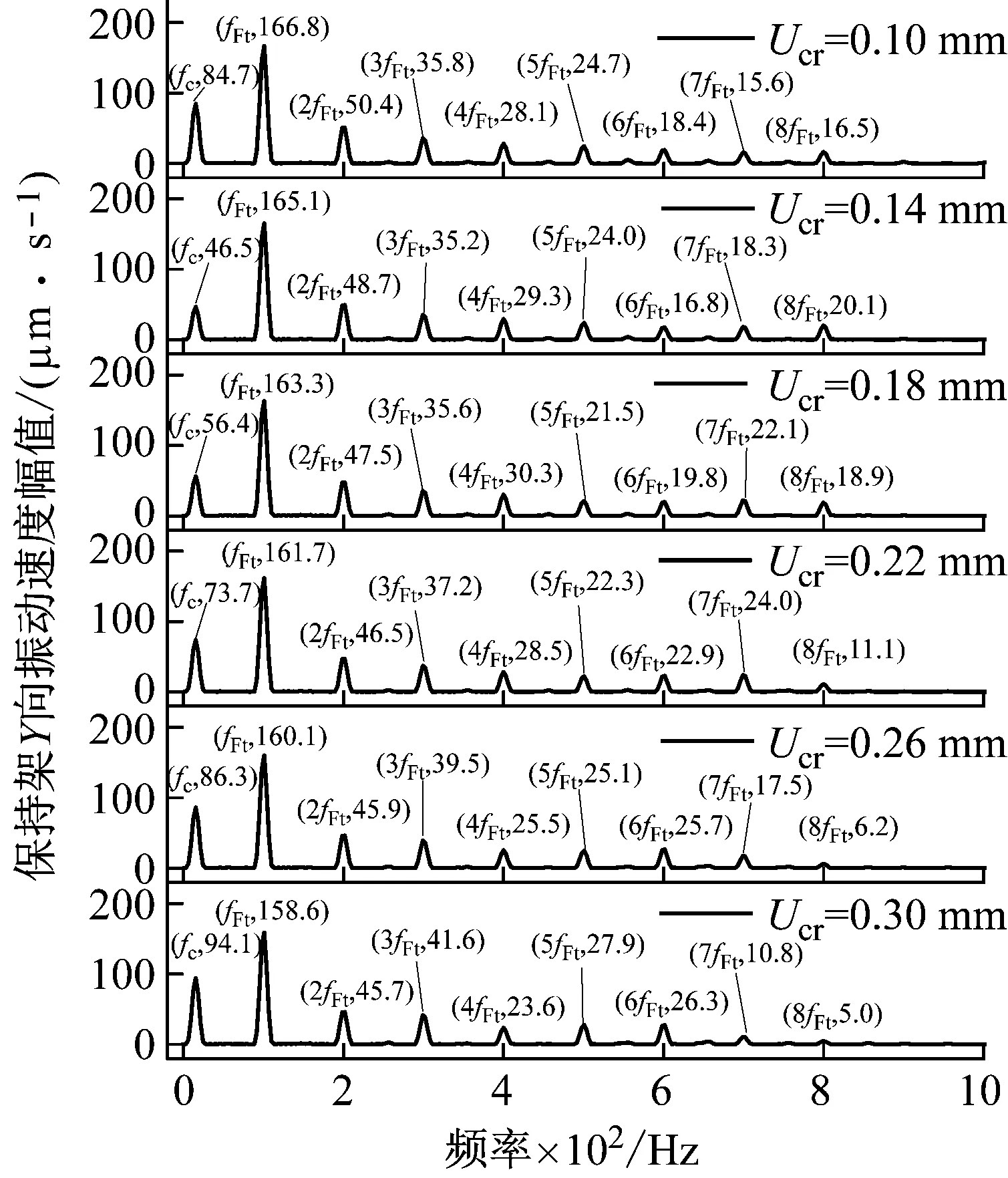
(a) Y向频谱

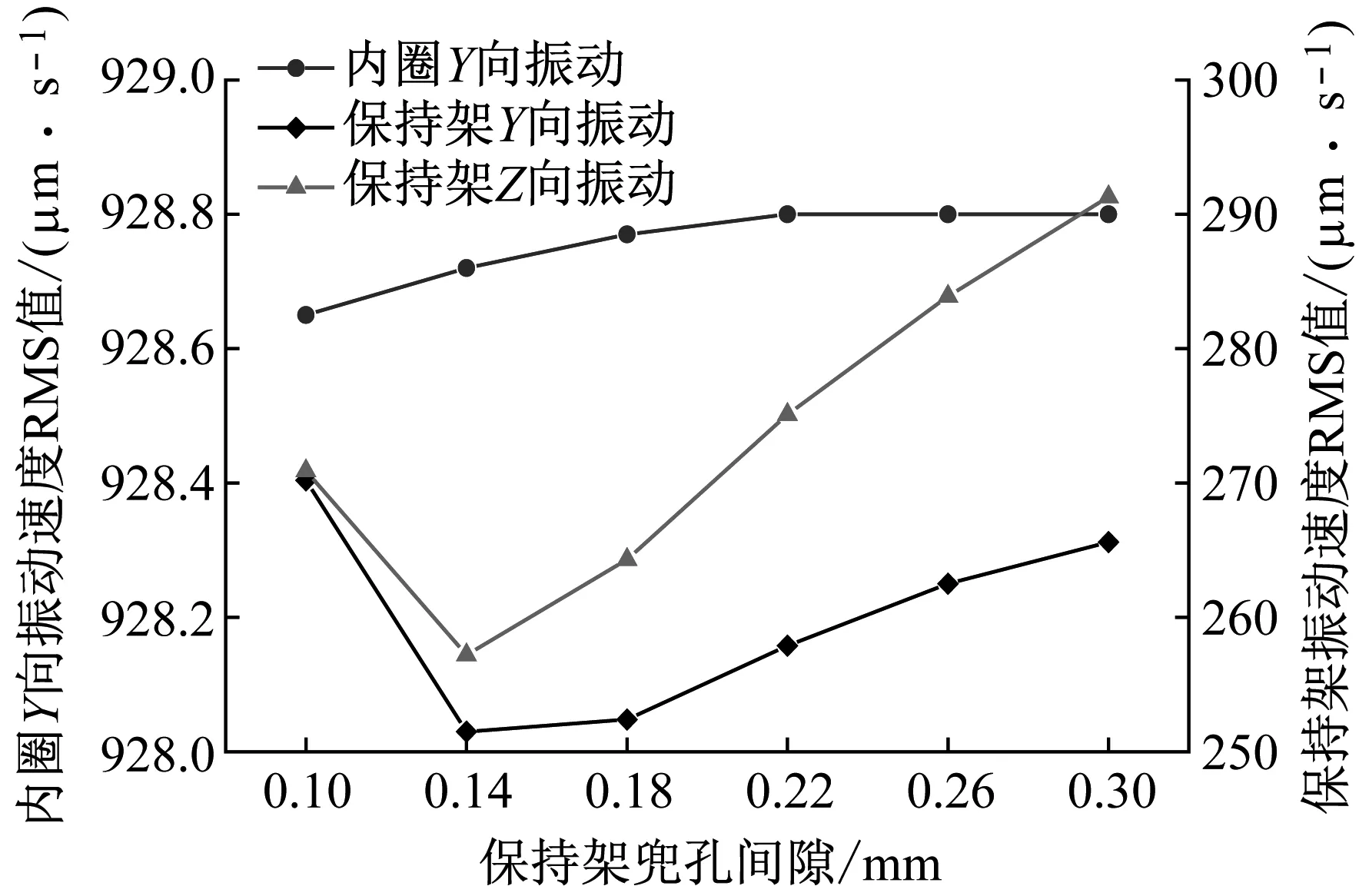
图26 保持架兜孔间隙对轴承振动及保持架振动的影响Fig.26 Effect of cage pocket clearance on bearing vibration and cage vibration

图26表明随着保持架兜孔间隙的增大轴承内圈的振动速度先缓慢增加后趋于平稳。但是，兜孔间隙对保持架自身振动影响较大，选取保持架兜孔间隙为0.14～0.18 mm时，最有利于降低保持架振动提高保持架稳定性。导致上述振动特性的主要原因是：时变载荷作用下保持架与钢球的相互作用更加复杂，过大或过小的保持架兜孔间隙都会增大保持架的振动。