基于改进极限学习机的水轮机运转状态识别

兰朝凤，宋博文，郭小霞

(哈尔滨理工大学 测控技术与通信工程学院，哈尔滨 150080)

随着居民用电量的增加，电网的安全可靠性已经成为了社会需要重视的一个问题。水力发电作为一种发电方式，保证水轮机安全稳定地运行，就显得至关重要。因此，及时为水轮机进行状态预测，是目前要解决的一个难题。

目前，国内外很多学者从理论研究、试验研究、数值模拟3个角度出发，进行水轮机运转状态识别[1-3]，取得了较好的进展。然而，这部分学者并没有直接展示水轮机信号与与水轮机运转状态的关系。从文献[4-5]可以看出，要想直接展示水轮机信号与水轮机运转状态的关系，实现水轮机运转状态识别的话，就要以信号预处理、特征提取、运转状态识别模型的构建为技术路线去实现。

合适的信号处理技术是信号预处理的重要部分。传统的信号处理方法比如傅里叶变换(Fourier transformation,FT)[6]，不能分析像水轮机信号这样的非平稳信号，为此，出现了像小波变换(wavelet transform,WT)[7]、经验模态分解(empirical mode decomposition,EMD)[8]、互补集合经验模态分解(complementary ensemble empirical mode decomposition,CEEMD)[9]这样的信号处理技术。文献[10]对信号进行CEEMD分解之后，用夹角余弦计算信号与IMF分量之间的相似度，判断噪声主导模态和信号主导模态之间的分界点，最后获得了较好的去噪效果。文献[11]用CEEMD，分析高水头混流式水轮机的稳定性。

水轮机故障的故障特征通常蕴含在水轮机信号里面，因此，要用合适的特征提取方法对水轮机信号进行特征提取。不少学者计算排列熵、能量矩、峭度等物理量以进行特征提取。其中，排列熵(permutation entropy,PE)是一种基于复杂性量度的非线性动力学参数，能有效地反映系统的特征。文献[12]用PE将IMF分量组成滚动轴承故障诊断模型的特征样本集，以实现轴承故障诊断，正确率为99.285 7%。

除了合适的信号处理技术和合适的特征提取方法，合适的水轮机运转状态识别模型也至关重要，部分学者用概率神经网络(probabilistic neural network,PNN)[13]、极限学习机(extreme learning machine,ELM)[14]、小波神经网络(wavelet neural network,WNN)[15]进行水轮机运转状态识别。ELM相较于PNN和WNN出现较晚，是一类基于前馈神经网络(feedforward neuron network,FNN)构建的机器学习方法，适用于监督学习和非监督学习问题，在分类、模式识别等方面有一定的应用[16]。ELM的权值和阈值影响其自身的性能，部分学者用PSO优化ELM的权值和阈值[17]。然而，PSO存在易陷入局部最优的缺点，这影响了PSO的性能。

针对上述文献提出的问题，本文提出基于SA-PSO-ELM的水轮机运转状态识别模型。在CEEMD中融合皮尔逊相关系数和小波方法对水轮机信号进行去噪。去噪之后，再利用CEEMD，对去噪之后的水轮机信号进行特征提取以构建水轮机运转状态识别模型的输入特征向量。最后，利用SA-PSO优化ELM的权值和阈值，将SA-PSO与ELM结合，提出基于SA-PSO-ELM的水轮机运转状态识别模型，并通过比较正确率、均方误差、决定系数3个指标，评价了本文提出的SA-PSO-ELM模型的性能。

1 基础理论

1.1 小波阈值去噪

小波变换(wavelet transform,WT)在低频时的时间分辨率较高，频率分辨率较低；在高频则相反，这符合低频信号变化缓慢而高频信号变化迅速的特点，是它优于傅立叶变换的地方。

WT进行信号去噪已经应用广泛。目前已经有很多种小波去噪方法，如极大值去噪、小波系数相关性去噪等，其中阈值去噪是一种效果比较明显、易于实现的去噪方法，其中又分为硬阈值和软阈值。

本文选取含噪矩形波信号，利用小波软阈值函数对其进行去噪并与硬阈值进行去噪进行对比，去噪前和去噪后的矩形波信号时域图如图1所示。

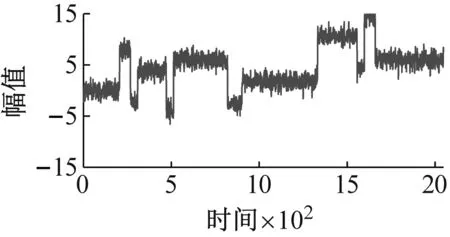
(a)含噪信号的时域图

由图1可知，小波软阈值去噪效果更好，能减少噪声对水轮机运转状态识别的干扰。

1.2 互补集合经验模态分解

为了更好地分析水轮机信号，本文针对传统EMD方法容易出现模态混叠的问题，利用CEEMD对水轮机信号进行成分分析。

经过CEEMD法分解之后的原信号，可以看作是多个IMF分量和一个残余量的和，即

(1)

式中，X(t)、t、r、IMFk分别为原信号、时间、残余量、第i个IMF分量。CEEMD法的重构误差较小，能有效地进行特征提取。

信号经CEEMD法分解后的所有IMF分量中，噪声含量较高的分量叫噪声主导模态，含量较低的分量叫信号主导模态。本文用皮尔逊相关系数确定噪声主导模态和信号主导模态的分界点，相关系数越大，IMF分量越与原始信号相似。皮尔逊相关系数的表达式为

(2)

式中，COV(X,Y)、ρX、ρY分别为协方差、变量X的方差、变量Y的方差。在判断IMF分量与原始信号的相似度时，可把原始信号当作X，IMF分量当作Y。

在特征选取时所选择的特征上，本文选排列熵作为CEEMD法所提取的特征参数。

2 智能算法、神经网络

2.1 原始算法和网络

2.1.1 粒子群算法

PSO源于对鸟类捕食行为的研究，有演化计算的优势。PSO首先在可解空间中初始化一群粒子，每个粒子都代表极值优化问题的一个潜在最优解，用位置、速度、适应值三项指标表示该粒子特征，通过适应度函数计算影响粒子优劣的适应值。PSO的流程图如图2所示。

图2 粒子群算法流程图Fig.2 Flow chart of particle swarm optimization algorithm

PSO的速度和位置更新可表示为

Vid=WVid+c1r1(Pid-Xid)+c2r2(Pgd-Xid)

(3)

Xid=Xid+Vid

(4)

式中：r1、r2在0～1之间随机取值；Vid、Xid分别为粒子速度、粒子位置；Pid和Pgd分别是粒子的个体最优值、全局最优值；c1和c2为学习因子；W为惯性权重。

PSO在前期要加强全局搜索能力，后期要加强局部搜索能力。因此，粒子群的相关参数不应一成不变，其惯性权重W和学习因子c1应当逐渐减小，而学习因子c2应当逐渐增大。学习因子的改进公式和文献[18]相同。惯性权重的改进公式为

(5)

式中：Wini、Wend分别为初始惯性权重、最终惯性权重；k为迭代次数；kmax为迭代次数最大值；∂等于1。

PSO在解决多峰值问题时，容易出现早熟现象从而陷入局部最优解。因此，如何避免PSO陷入局部最优解，本文将在2.1.2节的研究中提出避免陷入局部最优解的解决方法。

2.1.2 模拟退火算法

SA是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性，SA从某一较高初温出发，伴随温度参数的不断下降，结合概率突跳特性在解空间中随机寻找目标函数的全局最优解，即在局部最优解能概率性地跳出并最终趋于全局最优。SA的流程图如图3所示。

图3 模拟退火算法流程图Fig.3 Flow chart of simulated annealing algorithm

模拟退火算法能以一定概率接受较差解，具有跳出局部最优解，进入全局最优解区域的能力。因此，SA-PSO的算法精度较高，可一定程度上避免PSO容易陷入局部最优的问题。

2.1.3 极限学习机

ELM是基于前馈神经网络构建的机器学习系统，ELM在故障诊断(比如机械故障诊断)中得到了较好的应用。ELM的结构图如图4所示。

图4中，X1-Xn为ELM的输入变量，Wij、βjk分别为输入层和隐含层之间的输入权值、隐含层输出权值，Y1-Ym为ELM的输出变量。在ELM中，一旦Wij和隐含层的偏置确定了，隐含层的输出就确定了。在ELM中，只需要提前设定隐含层神经元的个数即可。

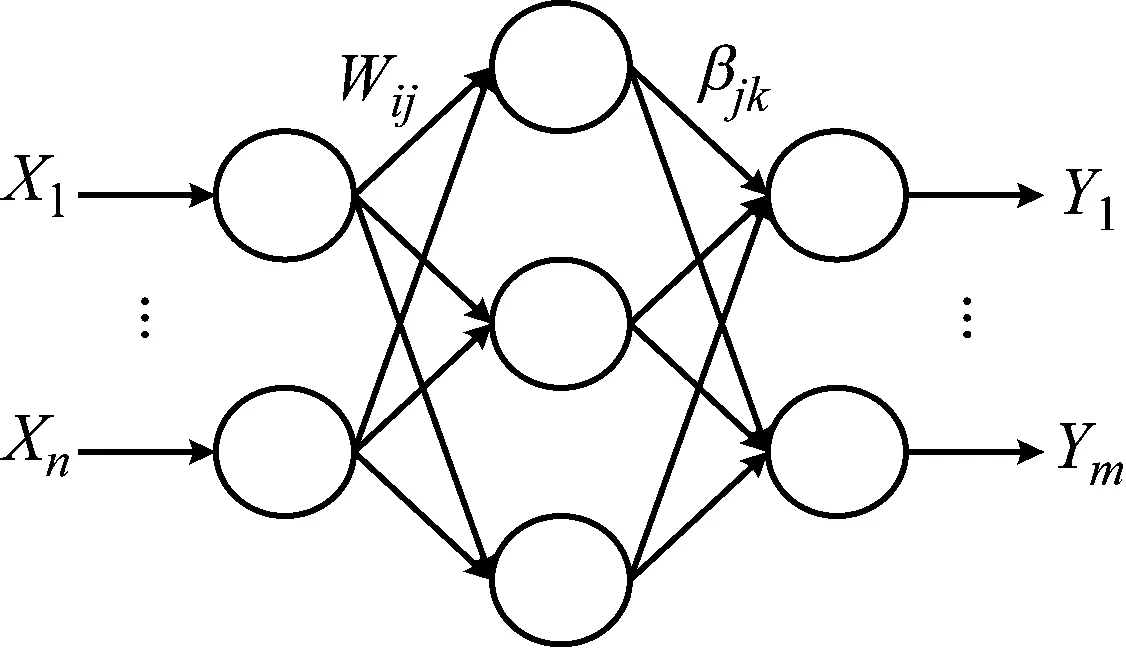
图4 ELM的结构图Fig.4 Structure diagram of ELM

2.2 本文预测模型的建立

由于ELM的输入权值和隐含层阈值是随机产生的，其稳定性较差，进而影响了其自身的性能。因此，本文将SA-PSO利用均方误差函数与ELM连接，通过SA-PSO优化ELM的阈值和权值，当均方误差不随迭代次数的增加而下降时，输出的权值和阈值即为优化后的权值和阈值，近而构建SA-PSO-ELM模型。

计算均方误差函数的表达式可写为

(6)

式中，yi、ti、及n分别为ELM的预测值、ELM的实际输出值及优化模型中训练集的样本个数。

SA-PSO-ELM的流程图如图5所示。

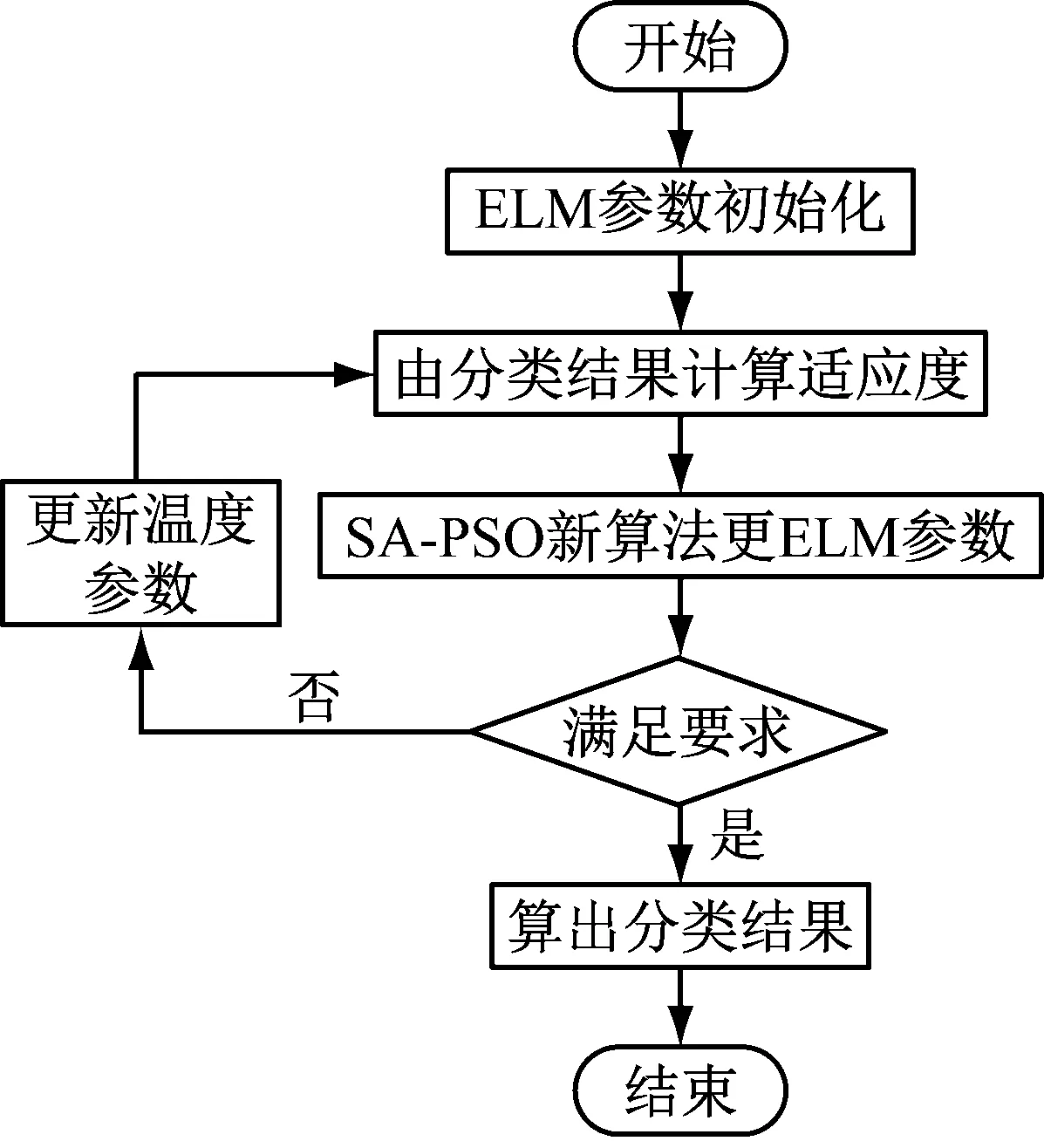
图5 SA-PSO-ELM流程图Fig.5 SA-PSO-ELM flow chart

本文构建的SA-PSO-ELM的演算过程如下：

步骤1ELM参数初始化；

步骤2由分类结果计算适应度；

步骤3更新ELM参数；

步骤4判断寻优曲线是否收敛且误差是否满足要求。如果收敛且满足要求，输出分类结果，否则返回步骤2。

3 数据处理与分析

3.1 试验环境与工况设置

尾水管的作用是引导进出转轮的水流，是水轮机的主要通流部件，是水轮机压力脉动测试时的主要部位，本文试验数据来自于用压力传感器采集的水轮机的尾水管的7个主要部位的信号：蜗壳进口、无叶区+Y、无叶区-Y、锥管+Y0.3D2、锥管-Y0.3D2、肘管外侧、肘管内侧。在采集数据的过程中，设置五种工况分别为正常状态、预警状态、报警状态、异常状态、故障状态。试验过程中，在每个部位安装1个传感器采集压力脉动数据，每个部位在每个运转状态下采集10 000个数据，数据的采样频率为4 kHz，试验装置含尾水管部分的外形如图6所示。

图6 试验装置尾水管的外形Fig.6 Apparance of draft tube of test device

试验因工况调整设有4个可变参数：导叶开度(mm)、单位转速(r/min)、流量(m3/s)、装置空化数。其中，装置空化数越小，水轮机的抗空化性能越差，当设置不同的工况参数时，水轮机运转状态从正常状态向预警状态、报警状态、异常状态、故障状态依次过渡。本试验中，采集水轮机信号时的水轮机的参数设置如表1所示。

表1 不同运转状态下的导叶开度、单位转速、流量、装置空化数Tab.1 Guide vane opening,unit speed,flow and cavitation number of the device under different operatingconditions

3.2 模态分界点的选取

为确定模态分界点，用CEEMD法对水轮机信号进行分解。本文只展示蜗壳进口部位的信号在正常状态下的CEEMD分解结果，分解成11个IMF，结果如图7所示。

由图7可知，从第3阶IMF分量开始，噪声含量逐渐下降，可近似认为分界点为3。为确定分界点估计的准确性，绘制IMF相关系数分布随IMF分量阶数变化的曲线，通过皮尔逊相关系数计算水轮机信号与IMF分量之间的相关性，分界点的选取准则为相似度曲线首次发生逆向转折的位置，结果如图8所示。

由图8可知，IMF4的出现，使相似度曲线的变化趋势发生首次逆向转折，分界点为3。可见，分界点估计的结果是正确的。

图7 CEEMD分解结果Fig.7 CEEMD decomposition results

图8 相关系数随IMF分量阶数变化的曲线Fig.8 Curve of correlation coefficient with IMF component order

3.3 频率成分分析

为确定水轮机信号的频率成分，对蜗壳进口部位在正常状态下的水轮机信号去噪之后，绘制频谱图，结果如图9所示。

图9 去噪之后的频谱Fig.9 Spectrum after denoising

由图9可知，水轮机信号的频率主要分布在0～60 Hz区间。可见水轮机信号的频率主要分布在低频段，对水轮机信号进行特征提取时主要提取水轮机信号在低频部分的特征。

3.4 特征提取

为提取水轮机信号的特征，对去噪之后的水轮机信号进行CEEMD分解，分解为10个IMF分量，同样选择蜗壳进口部位在正常状态下的水轮机信号。不同的IMF分量的频率成分不同，从分解得到的所有IMF分量中选择频率成分和水轮机信号的频率成分相近的IMF分量，进行特征提取。10个IMF分量的频谱图如10所示。

由图10可知，IMF3～IMF7分量为水轮机信号的主要频率成分，因此，进行特征提取时，选择IMF3～IMF7这5个分量。

对选用的IMF分量计算排列熵，并以排列熵构建水轮机运转状态识别模型的输入特征向量，每个特征向量的每一维是一个IMF分量的排列熵。设置水轮机运转状态识别模型的输入特征向量的个数为175个，每个运转状态的特征向量有35个，每个特征向量是5维的。

3.5 基于SA-PSO-ELM模型预测效果及分析

设置PSO的两个学习因子的取值分别为2.8和1.3，最大迭代次数为180，初始惯性值和迭代至最大代数时的惯性值分别为0.9和0.3，微粒的最大速度是1，设置SA-PSO-ELM的退火常数惯性权重为0.5。

特征向量输入个数为175个，选择125个作为训练样本，50个作为测试样本。模型的ELM输入层神经元个数、隐含层神经元个数、输出层神经元个数分别为5个、10个、1个。

为对比SA-PSO-ELM的正确率，绘制ELM、PSO-ELM、SA-PSO-ELM的分类结果图，结果如图11、图12所示(纵坐标的1、2、3、4、5分别代表水轮机运转状态的正常状态、预警状态、报警状态、异常状态、故障状态)。

(a) IMF1的频谱

图11 SA-PSO-ELM的分类结果图Fig.11 Classification results of SA-PSO-ELM

图12 ELM、PSO-ELM的分类结果图Fig.12 Classification results of ELM and PSO-ELM

由图11、12可知，ELM在样本编号为13-16、40预测错误，样本共计5个，因此正确率为90%，同时，由图11、12可知，PSO-ELM与SA-PSO-ELM的正确率为100%。

为定量分析ELM、PSO-ELM、SA-PSO-ELM的预测效果与均方误差和决定系数的关系，进行试验，结果如表2所示。

表2 不同模型下的预测结果Tab.2 Prediction results under different models

由表2可知，SA-PSO-ELM的均方误差为1.399 20，比ELM和PSO-ELM均小；SA-PSO-ELM决定系数为0.922 96，比ELM和PSO-ELM均大，即精度最高。且结合图11、12可知，SA-PSO-ELM的预测正确率为100%，由此表明本文提出的模型应用在水轮机运转状态识别上，效果较好。

4 结 论

本文针对水轮机的运转状态识别，提出了基于SA-PSO-ELM的水轮机运转状态识别模型，并作出如下总结：

(1) 用小波软阈值去噪对矩形波信号进行去噪，并用小波硬阈值去噪做对比，通过比较含噪信号的时域图和去噪后的时域图，确定了小波软阈值去噪较好的去噪效果。

(2) 利用皮尔逊相关系数，绘制水轮机信号和IMF分量之间的相关系数随IMF分量阶数变化的曲线，确定了K值估计的准确性。

(3) 用SA-PSO优化ELM的权值和阈值，构建水轮机运转状态识别模型SA-PSO-ELM。正确率、均方误差、决定系数分别为100%、1.399 20、0.922 96。同ELM、PSO-ELM相比，SA-PSO-ELM的正确率最高，均方误差最小，决定系数最大，SA-PSO-ELM的性能要好于ELM、PSO-ELM，更适合于水轮机运转状态识别。

随机森林(RF)、迁移学习在机械设备故障诊断中应用广泛，但是在水轮机故障诊断中应用不足。因此，下一步的计划是用RF或者迁移学习构建水轮机运转状态识别模型，识别水轮机运转状态，准确地诊断水轮机故障。