非饱和土刚性挡墙抗滑移稳定性上限分析

2023-01-31邓波杨明辉赵明华

湖南大学学报（自然科学版） 2023年1期

邓波，杨明辉，赵明华

（1.南华大学土木工程学院，湖南衡阳 421001；2.湖南大学土木工程学院，湖南长沙 410082）

针对挡土墙安全评估，其稳定性分析必不可少，且大都将墙后土压力作为重要荷载计算挡土墙稳定性系数.例如，Choudhury 等［1］采用Mononobe-Okabe法计算主动土压力，并基于拟静力法分析了考虑动水压力作用的挡墙抗滑移与抗倾覆稳定性；马少俊等［2］考虑了地震荷载的时间效应和相位差效应，并采用拟动力法推导了挡墙抗滑稳定性系数的计算表达式；Chakraborty 等［3］采用拟动力法估算了地震被动土压力和墙体惯性力，并给出了挡墙抗滑稳定性系数的闭合解；Pain 等［4］采用改进的拟动力法，将填土和墙体视为受水平简谐振动的黏弹性介质，并由此确定了地震作用下挡墙转动稳定性系数.上述方法均以极限平衡理论为基础，且需先确定土压力，并忽略墙体存在产生的影响.相比较而言，极限分析上限法避免了确定土压力的大小及作用位置，且核心在于构建墙土系统运动学相容的速度场，因而简化了求解过程，并被诸多学者广泛采用.例如，Li 等［5］运用简单块体法计算了重力式挡墙滑动破坏时的屈服加速度；刘杰［6］以挡墙-填土系统为研究对象，分别计算了考虑塑性临界深度影响的挡墙平移和转动的稳定性系数；彭文哲等［7］基于OptumG2 软件探讨了边坡坡度及抗剪强度对安全系数、最优桩位及桩长的影响，并根据参数分析结果拟合出安全系数公式；杨明辉等［8］考虑刚性挡墙平动变位模式情况，结合水平微分单元法，建立了墙后有限宽度土体的主动土压力分布表达式；Liu 等［9］采用多块体上限法推导了地震条件下涉水挡墙地震屈服加速度系数表达式；Li 等［10］分别建立了无限土条滑动模型和雨水入渗模型，并由此推导了地震-降雨耦合条件下地震屈服加速系数的计算公式.然而，相关计算普遍采用饱和土力学理论，难以考虑基质吸力对挡墙稳定性的影响.

值得注意的是，挡墙通常与非饱和土接触建造，并极有可能因季节性降雨和地下水位变化等因素显著改变土体水分状况，从而影响整个挡土结构系统的受力及变形特性.例如，有关文献报道了挡土墙及加筋土挡墙失效或大变形的案例［11-12］，均为在遭受连续暴雨情况下，导致基质吸力降低、土体及界面抗剪强度降低，进而引起挡土墙变形过大或发生破坏.近年来，考虑土体非饱和特性的挡墙稳定性研究已取得了一定进展，如Zhang 等［13］以非饱和土朗肯主动土压力理论为基础，计算了相对于墙趾的抗滑力矩与滑动力矩，并在均匀和线性基质吸力分布下，推导了挡墙抗倾覆埋深系数表达式；赵斌凯等［14］采用水平条分法，建立了均匀与线性两种基质吸力分布下筋材拉力及加筋长度的解析公式；Chehade等［15］采用离散化技术生成对数螺旋失效机制，考虑土体非均质性、不同地下水位及抗剪强度方程的影响，并基于拟动力法计算了维持加筋土挡墙稳定性所需的加筋强度；Deng 等［16］在稳定渗流条件下，考虑基质吸力、有效单位土重和抗拉强度截断的影响，并采用上限理论提出了一种评估加筋土挡墙内部稳定性的方法.可见，目前针对非饱和土加筋土挡墙稳定性分析已积累了部分经验，而刚性挡墙支撑非饱和填土研究多集中于土压力计算［17-19］，其稳定性分析方面仍较少见，有待开展进一步研究.

鉴于此，本文首先基于上限理论，给出了适用于非饱和土的功能平衡方程，并在此基础上推导了非饱和土挡墙抗滑稳定性系数的计算表达式；然后采用OptumG2数值软件和已有理论方法对比对本文方法进行验证；最后，对稳态渗流条件下挡墙及填土各参数对抗滑稳定性的影响进行深入分析，为工程中挡土墙设计提供可靠的理论依据.

1 非饱和土极限分析方法

1.1 广义有效应力原理

由于Bishop 有效应力忽略了土粒间的物理-化学应力，致使其无法准确描述非饱和土在高吸力段及低吸力段的特性，故Lu 等［20］提出全基质吸力范围的广义有效应力表达式：

式中：σ为总应力；ua为孔隙气压；σs为吸应力，其被定义为基质吸力（ua-uw）的唯一函数：

式中：uw为孔隙水压；Se为有效饱和度，见式（3）.

式中：α和n为VG 模型的拟合参数.α近似为进气值的倒数，其值为0～0.5 kPa-1；n与土体孔径分布相关，其值为1.1～8.5.一般地，土体中大尺寸孔隙数量越多，α值越大，且孔径分布范围越宽，n值越大.

若将式（2a）代入式（1）中，即简化为Terzaghi 有效应力关系式，因而采用式（1）表达的广义有效应力原理既完善了Bishop有效应力原理，又与Terzaghi有效应力原理形成有机统一.

1.2 考虑吸应力的上限定理

极限分析法是一种求解极限状态下土体结构稳定性的有效工具，从塑性角度讲分为相对真实解的严格上限法和下限法［21］.与下限法相比，上限法无需考虑应力分布，且简单易行，适用于土体稳定性评估.在总应力框架内，上限法一般表示为：任何运动学允许速度场的内部能量耗散率不小于真实外力所做功的功率.

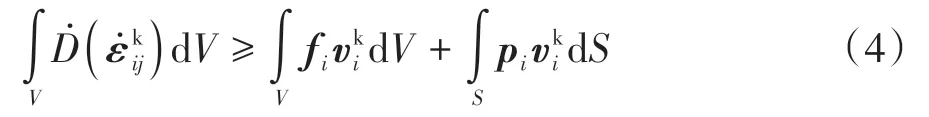
值得注意的是，基质吸力为应力状态变量，并非应力变量［22］，因而不能直接应用于式（4）中.相反，吸应力是基于尺度转换函数嵌入基质吸力作用的应力变量，故在有效应力框架内，采用吸应力表达的式（1）能与式（4）可靠结合，此时需在式（4）右侧累加吸应力和孔隙气压所做外力功率：

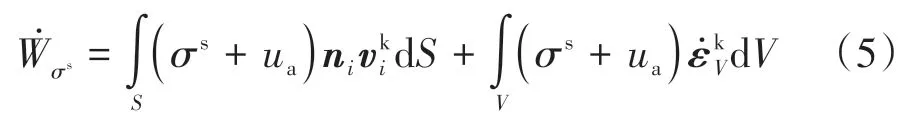
式中：为体积应变率矢量；ni为垂直于表面S的向外单位矢量.根据刚性块假设，破坏机构中不存在体应变，即，因而将式（5）代入式（4）中简化得：

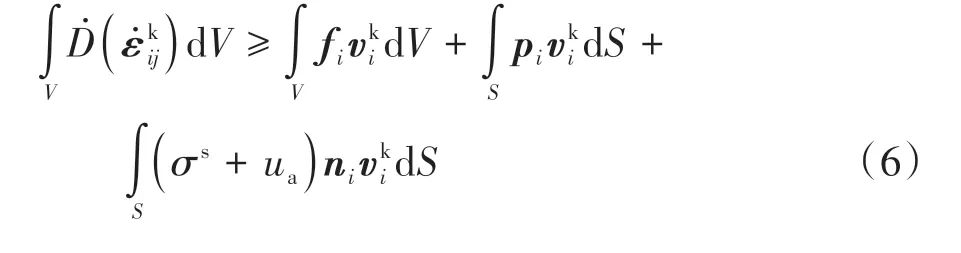
2 刚性挡墙-非饱和土系统稳定性分析

2.1 基本假设及破坏模式

为便于运用上限定理求解非饱和土挡墙滑动破坏模式下墙土系统的稳定系数，做如下假定：①墙土系统足够长且不考虑端部效应，以满足平面应变条件；②地下水位于墙趾以下z0深度处，即填土为非饱和土，且孔隙气压为大气压力，即ua=0；③墙后填土顶面作用有均布竖向超载qo；④参考库仑土压力理论，墙前、墙后填土的破裂面均为平面，且分别从墙趾、墙踵处形成；⑤填土、墙土界面分别满足抗剪强度公式（7）和（8）［18］，且符合相关联流动法则；⑥挡墙仅发生沿墙底方向的平移，不产生转动.

式中：τf为抗剪强度；（σn-ua）为净法向应力；c′和ϕ′分别为填土有效黏聚力和内摩擦角；和δ′分别为墙土界面有效黏结力和摩擦角.

挡墙滑动破坏模式如图1所示，墙土系统由3部分组成，即主动塑性区A1B1C1、被动塑性区A2B2C2和挡墙.取填土重度为γ1，墙后填土与水平向夹角为β1，墙背竖直，墙面与竖向夹角为β2，墙体重度为γ2，墙底宽为B，填土与墙面及墙背界面有效黏结力和摩擦角分别为和δw，填土与墙底界面有效黏结力和摩擦角分别为和δb.

图1 非饱和土刚性挡墙的滑动稳定性分析模型Fig.1 Sliding stability analysis model of rigid retaining wall with unsaturated soil

2.2 墙土系统能耗计算

2.2.1 速度矢量关系

图1所示的墙土系统包括5个速度间断面，即面A1B1、面A1C1、面A1A2、面A2B2及面A2C2，且主动塑性区A1B1C1与刚性区及墙背的相对速度分别为v1和v1w，墙底与刚性区的相对速度为vw，墙面与被动塑性区A2B2C2的相对速度为v2w.根据假定⑤，速度间断面上的相对速度与滑动面夹角为填土内摩擦角或墙土界面摩擦角，如在速度间断面A1C1、A2C2上的相对速度与滑动面夹角为ϕ′，在速度间断面A1B1、A2B2上的相对速度与滑动面夹角为δw，而在速度间断面A1A2上的相对速度方向与滑动面夹角为δb.若相邻块不发生重叠和相互嵌入，即满足构造的速度间断场是运动学容许的，则各速度矢量应满足如下关系：

根据式（9）（10）和图2 所示的三角关系，由正弦定理可以得到vw与其他速度之间的关系：

图2 相邻块的相容速度矢量Fig.2 Compatible velocity vector of adjacent blocks

2.2.2 几何关系

根据假定④，墙后填土主动塑性区和墙前填土被动塑性区均为三角形，其面积分别为：

刚性挡墙为梯形，其面积为：

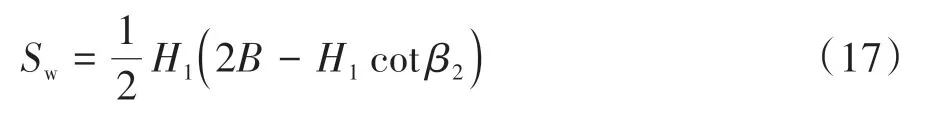
2.2.3 功率及能量耗散率

均布荷载qo作用在墙后填土顶面，其与v1方向的夹角为（π/2+ϕ′-ξ1），故其所做的功率为：

将式（10）代入式（17）中，有：

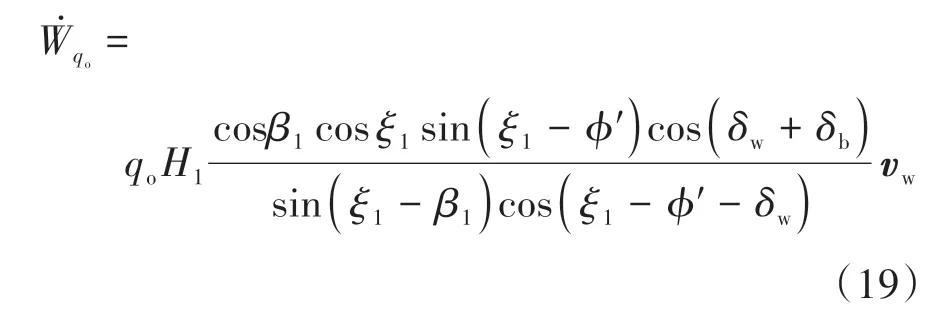
墙后主动塑性区A1B1C1重力方向为竖向向下，其与v1方向的夹角也为（π/2+ϕ′-ξ1），故其所做的功率为：

墙前被动塑性区A2B2C2重力方向为竖向向下，其与v2方向的夹角为（π/2+ϕ′+ξ2），故其所做的功率为：

将式（12）代入式（20）中，有：

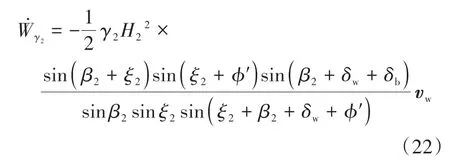
挡墙重力方向为竖直向下，其与vw方向的夹角为（π/2+δb），故其所做的功率为：

如前所述，非饱和填土中吸应力作用应当附加考虑在功率计算中.在图1 中，吸应力在A1C1间断面与v1方向的夹角为（π/2+ϕ′），在A1B1间断面上与v1w方向的夹角为（π/2+δw），在A1A2间断面上与vw方向的夹角为（π/2+δb），在A2B2间断面上与v2w方向的夹角为（π/2+δw），在A2C2间断面上与v2方向的夹角为（π/2+ϕ′），故吸应力在所有速度间断面上所做的功率为：

将式（11）～（14）代入式（24）中，有：

由于能量耗散主要发生在速度间断面上，即在面A1C1、A1B1、A1A2、A2B2、A2C2上，故沿着所有速度间断面的能量耗散率为：

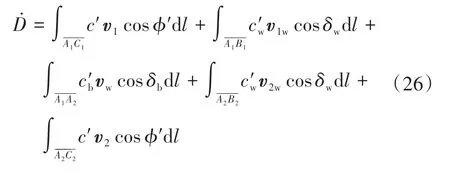
将式（10）～（13）代入式（25）中，有：

2.3 墙土系统稳定性系数计算

基于上限分析方法，采用能量法定义墙土系统的稳定性系数［23-24］：

在式（28）中，分子项表示有利于墙土系统稳定的外力做功功率和能量耗散率，即能量输出，而分母项则表示不利于墙土系统稳定的外力做功功率，即能量输入.该定义方法的优势在于，当选定某一稳定性系数时，即认为墙土系统在该稳定系数下能量达到平衡，若系统受到扰动，比如地下水位下降或蒸发导致吸应力增加，表明系统向外辐射能量，即提高了系统稳定性；又比如外荷载增加，表明系统吸收外界能量，即降低了系统稳定性.这从物理意义上解释了一个物体或系统的能量越大，越不易稳定的基本规律.特别地，稳定性系数Fs=1 表明系统处于能量的极限平衡状态，即一种临界破坏状态.

在确定土性参数和吸应力分布后，便可基于Matlab 编程对式（28）采用遗传优化方法求解稳定性系数Fs的最小值，以及对应的临界破裂角ξ1_cr和ξ2_cr.在利用优化方法求解时，必须满足式（29）所示的运动学约束：

3 计算结果验证与比较

3.1 与数值结果对比

采用OptumG2 软件建立挡墙-非饱和土系统分析模型，如图3 所示.在模型两侧设置切向约束，在模型底部设置完全约束，并在墙土接触面设置剪切节理模拟界面剪切特性，以及在墙底面施加法向约束实现墙体仅发生平移.为简化分析，土体基质吸力采用负压力水头代替，且仅考虑对土体施加相同的负压力水头，即假定基质吸力为均匀分布.

图3 挡墙-非饱和土系统稳定性的数值分析模型Fig.3 Numerical analysis model for stability of retaining wall-unsaturated soil system

对比计算结果如表1 所示.由表1 可知，本文计算的Fs大于数值模拟结果，主要由于OptumG2 软件无法模拟吸应力对墙土界面强度的影响，但两者随（ua-uw）和ϕ′的变化趋势一致，且两者的计算误差均小于10%，进一步验证了本文计算方法的可靠性.需要注意的是，表中数值结果为上限解和下限解的平均值，本文通过采用增加单元数量和优化网格的方法使上限解和下限解逼近，以保证两者计算差值在5%以内.此外，从表1可知，随基质吸力的增大，Fs先增大后减小，原因在于基质吸力无法唯一量化其对抗剪强度的贡献［25］，故在后续参数分析中采用吸应力代替基质吸力进行讨论.

表1 本文方法计算结果与数值结果比较Tab.1 Comparison between calculation results and numerical results

限于篇幅，选取（ua-uw）=10 kPa、ϕ′=20°时墙土系统的剪切耗散能进行分析，如图4所示.由图4知，土体破坏区由墙后主动塑性区及墙前的被动塑性区组成，且主动塑性区和被动塑性区形状接近平面，与本文计算假定相同.需要注意的是，这些塑性区域在有限元极限分析软件（OptumG2）中被分成若干刚性块体，因而在计算时容易在墙趾处出现压应力集中现象［26］.

图4 墙土系统的剪切耗散图Fig.4 Shear dissipation diagram of wall-soil system

3.2 与已有文献结果对比

为进一步验证式（28）的合理性，在饱和情况下与文献［6］中计算的稳定性系数（Fs）及对应的破裂角（ξ1_cr）进行对比.为与文献［6］中的计算条件保持一致，仅考虑主动塑性区的影响，即H2=0.采用的计算参数为：，其他参数见表2.

表2 本文方法计算值与其他方法计算值比较Tab.2 Comparison of the calculated values of the method in this paper with that of other methods

从表2 中结果可知，文献［6］中的Fs值略小于本文结果，原因在于文献［6］在计算Fs时考虑了墙后临界塑性深度，因而计算值更小一些，但总体上讲，两者计算的Fs和ξ1_cr差异最大值为12.5%，可见本文计算方法基本可靠.

4 影响因素分析

在实际工程中应用式（28）计算墙土系统稳定性系数时，需先借助数值方法确定基质吸力分布.为简化分析，本节采用Lu 等［27］提出的一维稳态渗流条件下的基质吸力分布进行参数讨论：

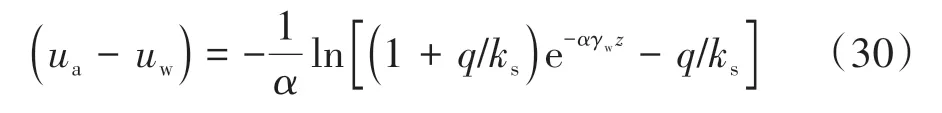
式中：q为垂直渗流量（其中，q＜0 表示入渗，q=0 表示静水，q＞0 表示蒸发）；γw为水的重度；ks为土体饱和渗透系数；z为地下水位埋深.

若将式（30）代入式（2b）和式（3）分别得到吸应力分布及有效饱和度分布如下：

基于式（31）和式（32），有必要探讨不同土体类型的吸应力及饱和度随深度的变化规律，特取Lu等［27］统计的4 种典型土体的水力学参数见表3，并假定这些土层分别处于3 种不同渗流状态：①入渗条件（q=-3.14×10-8m/s）；②静水条件（q=0）；③蒸发条件（q=1.15×10-8m/s）.

表3 不同土类型的水力学参数Tab.3 Hydraulic parameters of different soil types

由图5 可知，黏土层的吸应力随深度几乎呈线性变化，而饱和度随深度变化较小，原因在于黏性土的α值小，持水特性好.在粉土层中，吸应力和饱和度的分布形式与黏土层类似，但两者随渗流量的变化值变小.对于黄土层，吸应力对渗流量变化不太敏感.在砂土层中，不同渗流量对其吸应力和饱和度几乎无影响，且砂土层中的吸应力在地下水位附近有一个明显的峰值，之后随着离地下水位的距离的增加，吸应力大大减小.这种现象是由于毛细力是砂土中唯一的吸应力分量，且在存在表面张力的情况下需要空气-水界面，因而过于潮湿或干燥的条件会减少这些界面区域，并导致小的毛细管应力.此外，对比不同土体饱和度随深度的变化，黏土最小，粉土次之，黄土和砂土最大.以上分析表明，吸应力和饱和度变化取决于土体类型及深度，其对土体强度有重要影响，进而会影响对墙土系统的稳定性，因而有必要在计算时考虑其作用.

图5 不同渗流条件下土体吸应力及饱和度的分布Fig.5 Distributions of suction stress and saturation of soil under different seepage conditions

在后述参数分析中，若无特殊说明，取H2/H1=2，q0=30 kPa.

4.1 土体强度参数影响

如图6 所示，在相同的ϕ′和c′/（γH）值下，黏土中Fs值均大于砂土中对应值，表明黏土中吸应力比砂土中吸应力对墙土系统的稳定性影响更大.此外，砂土中Fs-c′/（γH）曲线变化率比同条件下黏土中相应的曲线变化得更快，表明相比黏土，砂土中黏聚力的变化对墙土系统稳定性更为敏感.

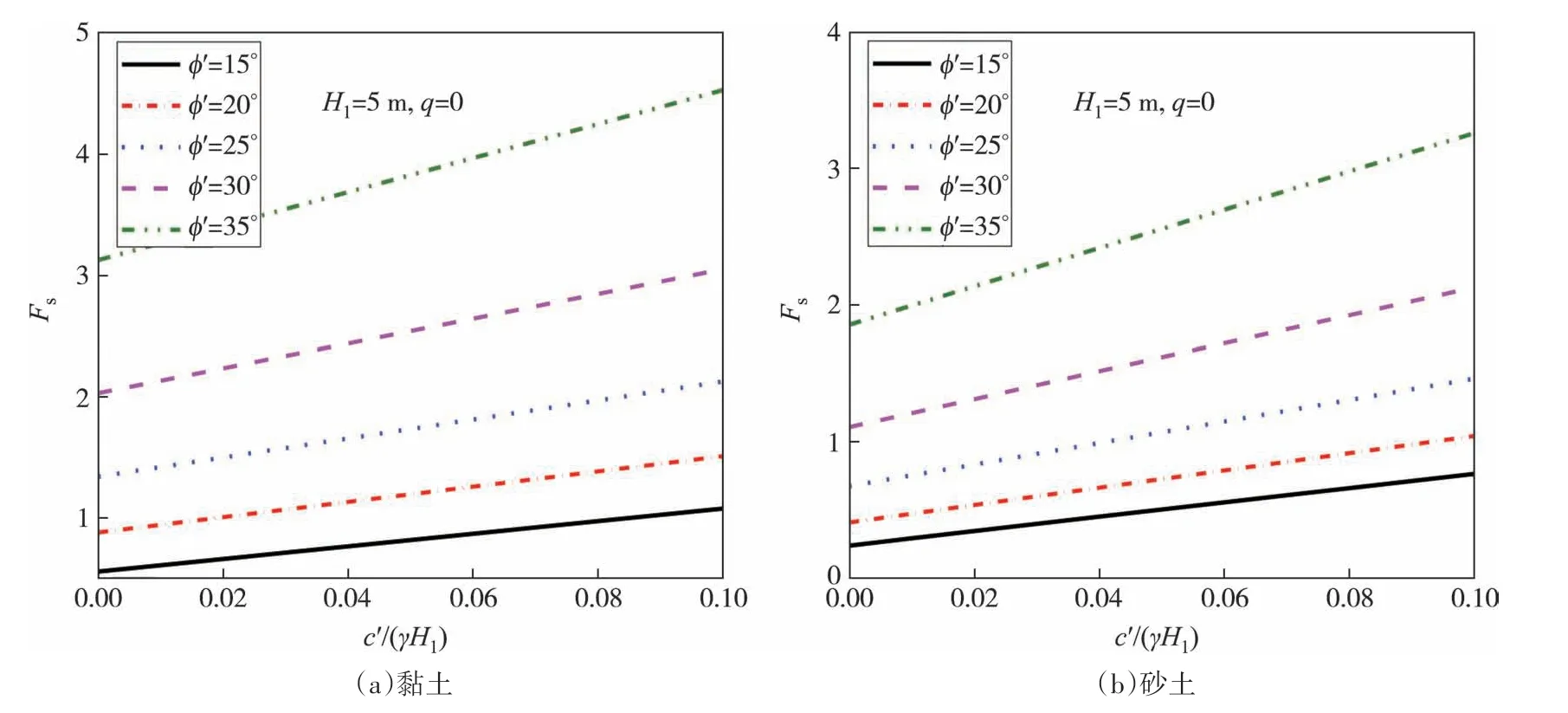
图6 不同ϕ′值下Fs与c′/γH1的关系Fig.6 Relationship between Fs and c′/γH1 at different ϕ′ values

4.2 进气值参数影响

如图7 所示，对于给定的n值，Fs随1/α值增大呈现先增大后保持不变，且当1/α取较小值时，并给定较小n值，此时Fs取较大值；反之，随1/α值的增大，对于不同的n值，各种曲线趋于在较高1/α值下接近Fs的恒定值.此外，对于高度较低的挡墙，不同n值对应的Fs值倾向于在较小1/α值处达到恒定值，表明不同n和1/α值的影响与挡墙高度是相关的，且吸应力对于高度较低的挡墙影响更明显.

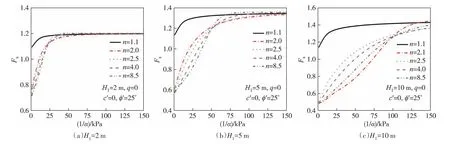
图7 不同n值下Fs与1/α的关系Fig.7 Relationship between Fs and 1/α at different n values

4.3 渗流量参数影响

图8给出了在3种特定渗流条件下的分析结果，包括蒸发（q=1.15×10-8m/s）、静水（q=0）和入渗（q=-3.14×10-8m/s）.相比无吸力情况，考虑吸力作用的Fs值更大，其中黏土和粉土最为明显.如，不同q值导致Fs值的影响可归纳为：蒸发＞静水＞入渗.此外，渗流量q值的影响在粉土中逐渐降低（见图8（b）），而在黄土（见图8（c））和砂土（见图8（d））中的影响几乎可以忽略不计，表明不同土层类型产生的基质吸力差异将影响墙土系统的稳定性.