冷弯薄壁型钢组合墙体简化计算模型研究
2023-01-31管宇周绪红石宇李松松聂少锋姚欣梅
管宇 ,周绪红 ,2,石宇 ,李松松 ,聂少锋 ,姚欣梅
(1.长安大学 建筑工程学院,陕西 西安 710061;2.山地城镇建设与新技术教育部重点实验室(重庆大学),重庆 400045)
在乡村振兴和新型城镇化发展过程中大力推广冷弯薄壁型钢结构体系,符合绿色建筑和装配式建筑的发展方向,可以提高建设效率、提升建筑品质、降低能耗,符合可持续发展的要求.
组合墙体作为冷弯薄壁型钢结构体系的主要承重和抗侧力构件,由墙架柱、上下导轨及轻质墙板通过自攻螺钉连接而成,其抗侧刚度和抗剪承载力主要由冷弯薄壁型钢骨架与外侧轻质墙面板之间的蒙皮效应产生.国内外学者对冷弯薄壁型钢组合墙体的抗剪性能进行了较为深入的研究.Xu 等[1]提出了冷弯薄壁型钢组合墙体的抗剪承载力和抗侧刚度的理论公式,该公式体现了螺钉间距对墙体抗剪性能的影响.Moghimi 等[2]和Velchev 等[3]通过试验研究了设置交叉钢带支撑的冷弯薄壁型钢墙体的抗剪性能,指出增强交叉钢带与螺钉连接可提高墙体的抗剪性能,增大钢带截面可提高墙体的抗侧刚度.周绪红等[4-5]基于冷弯薄壁型钢组合墙体抗剪试验结果,提出了考虑刚度退化和捏拢效应的组合墙体退化四线型恢复力模型.Yu 等[6-7]对冷弯薄壁型钢薄钢板剪力墙进行了抗震性能试验研究,破坏特征为钢板屈曲和螺钉连接破坏,应采用折减系数2w/h(w和h分别为墙体宽度和高度)以考虑高宽比对墙体承载力的影响.Nithyadharan 等[8-9]根据墙体抗剪试验过程中螺钉经历的倾斜、承压和脱开3 个破坏阶段,定义了墙体的弹性、屈服和破坏3 个阶段,并提出了适用于覆硅酸钙板组合墙体的滞回模型.Wu等[10]通过抗剪性能试验对填充轻质材料的冷弯薄壁型钢组合墙体的受力特性及破坏特征进行了研究分析.袁泉等[11]建立了中间支撑冷弯薄壁型钢灌浆墙体的有限元模型,通过抗剪性能模拟分析指出Z 形斜撑可有效解决钢拉条引起的墙体偏心受力问题,显著提高墙体的抗剪承载力.Xu 等[12-13]对覆秸秆板内填高强轻质泡沫混凝土组合墙体进行了抗震性能研究,采用规范公式计算了该组合墙体的抗剪承载力.Zhang等[14]提出了压型钢板蒙皮轻钢组合墙体的水平侧移计算方法.Yu 等[15]通过试验研究表明压型钢板开缝可在保证抗剪承载力较高的同时提高冷弯薄壁型钢压型钢板组合墙体的延性.
现有成果主要集中于墙体抗剪试验研究和抗剪理论分析,对组合墙体计算模型的研究相对较少.基于此,根据冷弯薄壁型钢组合墙体的侧向变形模式,建立了组合墙体的简化计算模型,推导了模型中对角弹簧轴向刚度的计算方法.通过冷弯薄壁型钢组合墙体拟静力试验的模拟分析和冷弯薄壁型钢结构房屋的弹性动力时程分析,验证了组合墙体简化计算模型的正确性,并明确了组合墙体简化计算模型的适用范围,可为轻钢结构的抗震设计提供参考.
1 组合墙体简化计算模型
在水平荷载作用下,冷弯薄壁型钢组合墙体的侧向变形包括剪切变形Δs、弯曲变形Δb和倾倒变形Δr,见图1.其中,剪切变形为覆面板的剪切变形Δ1与覆面板上螺钉滑移产生的剪切变形Δ2之和;弯曲变形为两端墙架柱拉、压产生的变形;倾倒变形为锚栓拔起使墙体转动所产生的变形,而墙架柱脚的抗拔螺栓可有效抑制墙体发生倾倒,可忽略倾倒变形Δr产生的影响.因此,在水平荷载作用下组合墙体侧向变形以剪切变形和弯曲变形为主.

图1 组合墙体的变形示意图Fig.1 Deformation diagram of composite wall
组合墙体仅发生剪切变形的简化计算模型见图2,其中上导轨和两侧墙架柱忽略弯曲变形的影响,采用桁架杆件进行分析,杆件间采用铰接约束.

图2 组合墙体仅发生剪切变形的简化计算模型Fig.2 Simplified calculation model of composite wall with shear deformation
覆面板主要承担剪力,等效为非线性对角弹簧以抵抗侧向荷载,连接方式为铰接约束.参考日本轻钢设计手册[16]和日本建筑学会木质结构设计规范[17]提出的墙体等代拉条法,可推导墙体剪切变形Δs的计算公式.如图3 所示,覆面板剪切变形Δ1可参照剪切胡克定律(τ=G·γ)计算得到,见公式(1)(2).


图3 覆面板剪切变形Fig.3 Shear deformation of cladding panel

式中:τ为切应力;γ为切应变;G为覆面板的剪切模量;P为水平荷载;H为墙体高度;L为墙体宽度;t为覆面板厚度.
参照图4 计算覆面板上自攻螺钉滑移产生的剪切变形Δ2,简化分析时假定组合墙体周边每个自攻螺钉均匀受力,不考虑组合墙体中间墙架柱与覆面板间自攻螺钉的滑移.当组合墙体高宽比(H/L)与相应边自攻螺钉数目的比值相等时,组合墙体周边每个自攻螺钉受力相同,即墙体宽度方向,周边自攻螺钉个数为n,则墙体高度方向,周边自攻螺钉个数为

图4 覆面板螺钉滑移变形Fig.4 Screw slip deformation of cladding panel
在水平荷载P作用下,单个自攻螺钉承担剪力为N1=P/n,对应的自攻螺钉滑移值为S1;在水平荷载P=1 作用下,单个自攻螺钉承担剪力为.根据虚功原理,覆面板上自攻螺钉滑移产生的剪切变形Δ2的计算方法见公式(3)(4).
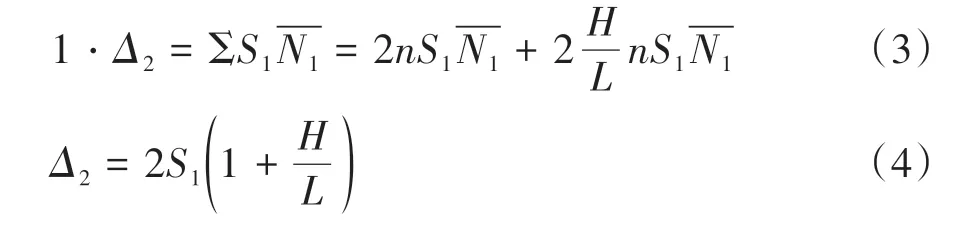
假定当自攻螺钉承担剪力达到抗剪承载力设计值Nv时,对应的自攻螺钉滑移值为Sv;当自攻螺钉承担剪力为N1<Nv时,对应的自攻螺钉滑移为S1,则:

将公式(5)代入公式(4)得:

结合公式(2)和(6),组合墙体的剪切变形Δs计算结果见公式(7).
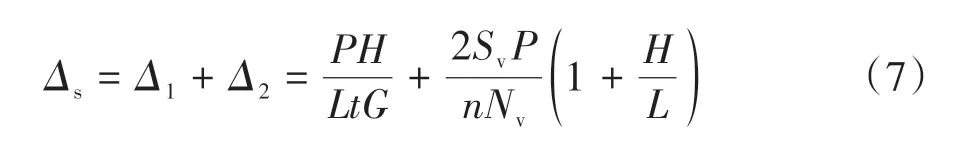
如图2,简化计算模型中侧向位移Δs的计算方法见公式(8)~(10).

式中:Ft为对角弹簧承受的轴力;Δt为对角弹簧的伸长量;kt为对角弹簧的轴向刚度;θ为对角弹簧与墙体宽度方向的夹角.
联立公式(7)和(10),得到对角弹簧轴向刚度kt的计算方法,见公式(11).

对于实际工程中开设门窗洞口的组合墙体,参照日本规范建议的墙体等代拉条法,考虑组合墙体开洞处上、下墙体的贡献作用,按照墙体开洞位置将组合墙体划分为不同尺寸的区格,根据区格的长、宽尺寸,覆面板材料属性以及周边自攻螺钉数量与滑移性能,按照公式(11)计算得到不同墙体区格的对角弹簧刚度.综上,冷弯薄壁型钢组合墙体考虑剪切变形和弯曲变形的简化计算模型见图5,该模型采用非线性对角弹簧模拟分析组合墙体的剪切变形,采用梁式杆件模拟分析组合墙体的弯曲变形.

图5 组合墙体考虑剪切变形和弯曲变形的简化计算模型Fig.5 Simplified calculation model of composite wall considering shear deformation and bending deformation
2 组合墙体拟静力试验模拟分析
为研究冷弯薄壁型钢组合墙体的侧向变形能力,对5 个未开洞和2 个开洞的2.4 m×3 m(宽×高)的组合墙体进行了抗剪性能试验研究[4-5].组合墙体试件基本参数见表1,典型试件构造见图6.采用ABAQUS 有限元软件对组合墙体简化计算模型的正确性进行验证,WA2 试件和WB3 试件有限元模型见图7.墙体上导轨采用桁架单元T3D2来模拟,单元网格尺寸取为100 mm.墙架柱采用梁单元B31 进行模拟,单元网格尺寸取为100 mm.钢材采用双折线本构模型以及von Mises屈服准则,其应力-应变关系参照材性试验确定[4-5].耦合上导轨所有节点施加水平位移以模拟位移加载模式,约束墙架柱柱脚节点所有自由度以模拟固端约束.在墙体各区格对角两个节点间建立弹簧连接约束,连接类型为Axial,受力行为定义为非线性,荷载与位移关系按照公式(11)计算,对应不同受力阶段的荷载-位移曲线见图8.

表1 组合墙体试件基本参数Tab.1 Basic parameters of composite wall

图6 冷弯薄壁型钢组合墙体构造Fig.6 Construction of cold-formed thin-walled steel composite wall

图7 有限元分析模型Fig.7 Finite element analysis model

图8 对角弹簧荷载-位移曲线Fig.8 Load-displacement curve of diagonal spring
有限元分析得到墙体WA2 和墙体WB3 在弹性阶段的变形云图见图9,可知组合墙体变形结果与简化计算模型变形图以及试验结果吻合较好.7 个组合墙体试验荷载-位移曲线与有限元分析结果对比见图10,不同受力阶段组合墙体承载力指标对比见表2.由图表可知,组合墙体简化计算模型能较好地模拟组合墙体试件弹性阶段的受力性能,有限元分析结果与试验结果误差小于15%,表明采用图5中组合墙体简化计算模型来分析组合墙体在弹性阶段的抗剪性能是合理的,可满足基于弹性的设计要求,并为冷弯薄壁型钢结构住宅的弹性动力时程分析提供参考.在屈服阶段和极限阶段,墙体承载力有限元分析结果与试验结果误差小于10%,而墙体侧移有限元分析结果与试验结果误差超过20%,表明组合墙体简化计算模型不能准确模拟墙体在弹塑性阶段的剪切变形,主要原因为推导组合墙体剪切变形的过程是建立在弹性条件下,不符合组合墙体在弹塑性阶段的受力特性.

图9 有限元模型变形图与试验对比Fig.9 Finite element model deformation diagram compared with test

图10 简化计算模型荷载-位移曲线有限元与试验对比Fig.10 The load-displacement curves of simplified calculation model on finite element compared with the test

表2 组合墙体承载力指标试验与有限元对比Tab.2 Test results of composite wall bearing capacity index compared with finite element results
组合墙体试验试件和有限元分析模型的单位长度受剪承载力设计值见表2,与《低层冷弯薄壁型钢房屋建筑技术规程》(JGJ 227—2011)[18]和《冷弯薄壁型钢多层住宅技术标准》(JGJ/T 421—2018)[19]对比可知:组合墙体单位长度的受剪承载力设计值与规范设计值较为接近,而误差产生的原因为组合墙体试件构造与规范中给定墙体构造不相同,规范中规定的墙体受剪承载力设计值并不能真实反映试验试件的抗剪性能.
3 轻型钢结构房屋弹性动力时程分析
文献[20]对3 层足尺的冷弯薄壁型钢结构房屋进行了振动台试验,试验模型长度和宽度均为5.1 m,层高为3 m,平面图和立面图见图11.墙架柱规格为C90 mm×35 mm×10 mm×1 mm,钢材为S350GD+Z 钢,内墙覆面板为10 mm 厚石膏板,外墙覆面板为 12 mm 厚OSB 板.楼盖采用钢桁架梁上覆18 mm 厚OSB 板的组合形式.屋架采用钢桁架,屋面板为 12 mm厚OSB板.

图11 试验模型平面图和立面图(单位:mm)Fig.11 Plan and elevation of test model(unit:mm)
采用ABAQUS 有限元软件建立3 层冷弯薄壁型钢结构房屋模型,见图12.组合墙体参照图7 建立,上、下导轨采用桁架单元T3D2 模拟,单元网格尺寸取为200 mm;墙架柱采用梁单元B31模拟,单元网格尺寸取为200 mm.对角弹簧采用非线性弹簧连接单元模拟,连接类型为Axial,弹簧轴向刚度参数按照公式(11)计算.覆面板自重采用集中荷载的方式施加至上导轨两端.组合楼盖和屋盖结合试验结果确定为刚性楼盖,采用壳单元S4R 模拟,单元网格尺寸取为400 mm.钢材采用双折线本构模型以及von Mises 屈服准则,其应力-应变关系参照材性试验确定[20].石膏板和OSB板简化为各向同性板件,材料参数参照材性试验确定[20].在材料属性中定义瑞利阻尼参数,阻尼比采用3%.在坐标系Z向定义重力加速度g=9.8 m/s2以模拟结构自重,楼、屋面活荷载采用均布荷载模拟.约束墙架柱柱脚节点所有自由度以模拟固端约束.

图12 3层房屋有限元模型Fig.12 Finite element model of three-storey building
3.1 模态分析
有限元模态分析得到模型前3 阶自振频率见表3,前3 阶振型见图13.由图和表可知:有限元模型的前3 阶振型均为整体变形,其中1 阶振型为沿Y向的平动,2阶振型为沿X向的平动,3阶振型为绕Z向的扭转.有限元模型分析得到房屋自振频率和周期与试验结果吻合较好,误差小于10%,表明有限元模型可较好地模拟房屋动力特性,且简单、合理.

表3 模型前3阶自振频率及周期Tab.3 The first three natural frequencies and periods of the model
3.2 弹性动力时程分析
按振动台试验加载工况[20],见表4,释放有限元模型墙架柱柱脚节点X和Y方向自由度,施加7 度和8度多遇El Centro调幅波,对有限元模型进行弹性动力时程分析.有限元模型在4 个工况下1 至3 层最大加速度放大系数变化曲线试验与有限元对比见图14,最大相对位移变化曲线试验与有限元对比见图15.

图14 最大加速度放大系数变化曲线试验与有限元对比Fig.14 Test results of maximum acceleration amplification coefficient variation curves compared with finite element results

图15 最大相对位移变化曲线试验与有限元对比Fig.15 Test results of maximum relative displacement variation curves compared with finite element results
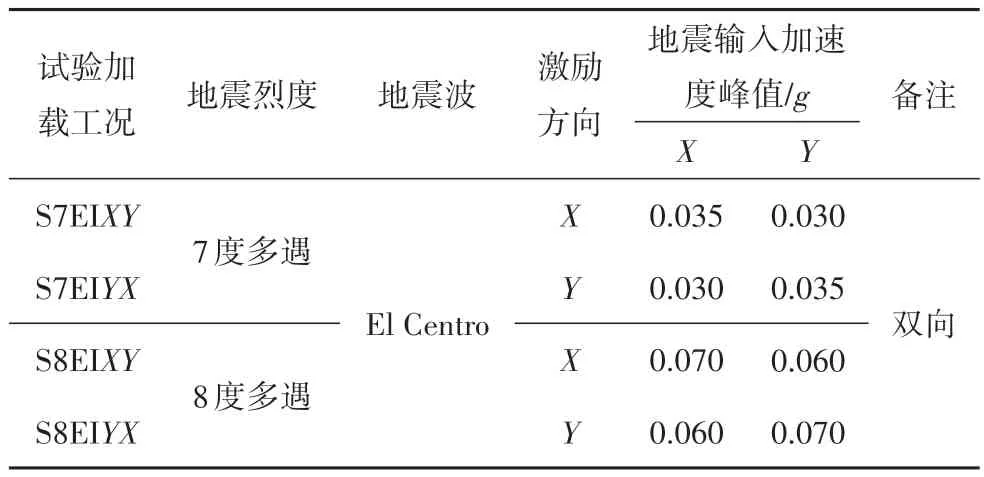
表4 有限元模型加载工况Tab.4 Loading condition of finite element model
由图可知:在7 度多遇和8 度多遇地震作用下,有限元模型1~3 层相同测点加速度峰值和最大相对位移试验结果与有限元分析结果吻合较好,误差小于15%,最大加速度放大系数变化曲线和最大相对位移变化曲线试验结果与有限元分析结果变化规律和整体趋势相近.误差主要出现在模型2层和3层在Y向的加速度响应和位移响应,原因为3 层房屋模型先后经历了一系列的试验加载工况,出现了结构损伤累积,如抗拔件松动、覆面板开裂等破坏现象,试验模型的整体性降低,而有限元模型较为理想,仅对单一加载工况进行模拟,未能考虑房屋模型经历多次加载工况而造成的损伤累积对房屋刚度的折减.因此,有限元模型能较合理及准确地模拟3 层冷弯薄壁型钢结构房屋在多遇地震作用下的动力响应,有限元模型简单、合理.
同时,图5 建立的组合墙体简化计算模型能较好地应用于冷弯薄壁型钢结构住宅的弹性动力时程分析,对工程设计和数值分析具有较好的应用价值.
4 结 论
基于冷弯薄壁型钢组合墙体简化计算模型,通过对组合墙体抗剪性能试验和3 层房屋振动台试验的模拟分析,得出以下结论:
1)在水平荷载作用下,组合墙体的侧向变形以剪切变形和弯曲变形为主.将覆面板等效为非线性对角弹簧以分析墙体的剪切变形,将墙架柱等效为梁式杆件以分析墙体的弯曲变形.推导出对角弹簧的轴向刚度计算方法.
2)基于墙体等代拉条法建立的组合墙体简化计算模型适用于结构的弹性分析,当结构进入弹塑性状态时,该模型会出现较大误差.基于组合墙体简化计算模型和刚性楼板假定建立的3 层冷弯薄壁型钢结构房屋有限元模型能较好地模拟轻钢房屋的动力特性以及多遇地震作用下的动力响应.
3)在工程设计时,若需要对组合墙体进行全过程模拟或对整体房屋进行弹塑性动力时程分析,建议采用试验测取的荷载-位移曲线来计算对角弹簧的轴向刚度或在简化计算模型的对角弹簧单元中引入塑性本构和损伤机制以满足弹塑性设计要求.
