基于卡尔曼滤波改进压缩感知算法的车辆目标跟踪

2023-01-31周云胡锦楠赵瑜朱正荣郝官旺

湖南大学学报（自然科学版） 2023年1期

周云，胡锦楠，赵瑜，朱正荣，3，郝官旺

（1.湖南大学土木工程学院，湖南长沙 410082；2.工程结构损伤诊断湖南省重点实验室（湖南大学），湖南长沙 410082；3.长沙市建设工程质量安全监督站，湖南长沙 410016）

桥梁是公共交通的咽喉，随着交通流量的激增，交通堵塞等交通事故成为了危及桥梁结构安全的隐患.交通实时监测成为了改善通行环境、保障交通安全和桥梁安全的有效途径.传统监测系统依赖于接触式传感器，存在传输距离受布线长度限制、安装更换困难以及无法灵活移动等缺点.采用非接触式视频跟踪技术对桥梁上的运动车辆进行实时跟踪，可以有效克服上述缺陷，获得连续、稳定、真实的运动轨迹，对桥梁健康监测具有重要意义.

在结构健康监测领域，基于计算机视觉技术的非接触式机器视觉监测技术具有测试精度高、无需封闭交通等优点，成为了近几年的研究热点.Zaurin等［1］提出了一种基于计算机视觉的桥梁监测技术，该技术使用边缘背景模型，完成了从视频帧图像中进行检测、分类和跟踪车辆的工作.Catbas 等［2］采用机器视觉跟踪技术逐帧分析视频帧中的车辆信息，实现了对视频帧图像中车辆的分类和位置识别.Chen 等［3］提出采用非接触式机器视觉技术对桥梁上移动车辆的时空分布进行识别，同时，基于BWIM 系统对车辆荷载的识别，使用背景差分法对视频帧中的车辆进行匹配，然后采用粒子滤波技术完成对移动车辆的跟踪工作.潘迪夫等［4］提出了一种多相关滤波器组合的目标跟踪方法，分别通过位置跟踪相关滤波器和尺度评估相关滤波器对目标进行准确定位和尺度估计，提高了目标跟踪算法的定位精度以及尺度估计的准确性.为提高在机器视觉监测技术中图像识别的数据获取以及处理能力，压缩感知理论利用特定的随机测量矩阵将高维信号投影至低维空间上，并通过最优化问题求解方式对原始信号进行重构［5］，基于压缩感知的目标跟踪算法有效地避免了对冗余信息的计算处理过程，使得该算法计算量小、跟踪效率高.Chen等［6］提出了一种基于压缩感知直接检测红外图像序列中小目标的新的自适应背景减影方法.修晓玉等［7］提出一种基于压缩感知理论的天文遥感图像小运动目标的检测方法，研究表明该方法能够准确地检测小运动目标，并实现精确定位.Qin等［8］利用稀疏信号的稀疏阶数进行压缩信号检测，该方案需要的压缩样本数较少且不需要稀疏信号支持先验信息.Zhang 等［9］提出了一种快速压缩跟踪算法，将降维特征分类与粗略-精细检测策略相结合，大大降低了算法运行成本.孔军等［10］提出了一种基于高斯差分图的压缩跟踪算法，从高斯差分图中提取特征并作为算法的输入，该算法对于尺度、纹理及光照变化具有较强鲁棒性，需要计算整幅图像的余弦相似度，因而算法复杂度较高.然而基于目标外观表达进行跟踪的方法具有一定的局限性，对目标的多种外观表达能力有限，对相似物体之间的区分表达能力较弱，容易导致跟踪失败或跟踪误差累积而产生跟踪漂移.

1960 年，Kalman 提出了基于状态空间递推滤波的卡尔曼滤波算法，它是一种自回归最小方差意义下的估计，采用递推方式处理的滤波器算法，能够在包含噪声及不完整的测量信号的系统中，估算出相应的状态量.随着计算机技术的迅猛发展，卡尔曼滤波算法的应用逐渐得到了广泛的研究［11］.Weng 等［12］使用自适应卡尔曼滤波器的视频目标跟踪设置自适应卡尔曼滤波器的系统模型，实现了跟踪过程中运动模型的构建，并在色相-饱和度-强度颜色空间中使用运动目标的主色，作为在连续视频帧中检测运动目标的特征.Li等［13］的研究表明，自适应卡尔曼跟踪算法具有较好的鲁棒性和实用性.王江等［14］提出了一种基于Kalman 滤波和直方图匹配的双目视觉跟踪方法，研究表明该算法能有效减少跟踪目标偏移或者消失的情况，取得良好的跟踪效果.Kumar等［15］基于最佳递归数据处理算法对卡尔曼滤波器的速度和硬件进行优化，用于过滤2D 目标跟踪中的噪声.韩锟等［16］提出一种融合运动状态信息的高速目标跟踪算法，该算法通过引入卡尔曼滤波算法在相关滤波跟踪失败时修正预测位置，提高了算法的跟踪精度.王敏敏［17］将快速压缩跟踪算法与卡尔曼滤波器相结合，设计了一种自适应算法切换策略，同时根据目标尺寸选择相应的目标检测算法，实现小目标多尺度检测，研究表明，该算法可以实现大小渐变目标的实时跟踪.

卡尔曼滤波算法通过不断更新目标的状态来跟踪目标或协助跟踪过程，可有效改善基于外观特征的目标跟踪质量，降低物体边界跟踪误差，缩小候选跟踪区域范围，然而，目前土木工程领域利用卡尔曼滤波算法进行车辆目标跟踪的研究相对较少.此外，传统的基于压缩感知技术的目标跟踪算法（Compressed sensing tracking algorithm，CT）受跟踪背景变化影响较大，存在跟踪点漂移、目标跟踪结果不稳定以及波动较大等问题.因此，本文采用卡尔曼滤波算法对压缩感知目标跟踪算法的结果进行修正，实现了较为精确的目标跟踪.首先，通过传统压缩感知目标跟踪算法获得跟踪结果；其次，基于上一帧跟踪轨迹，利用卡尔曼滤波预测本帧的跟踪轨迹，与本帧的实际跟踪轨迹相比较，利用卡尔曼系数对预测值与跟踪值进行修正，获得本帧图像目标跟踪结果；最后，根据本帧目标跟踪的目标框坐标及尺度，利用调整后的跟踪目标范围在其周围对下一帧图像进行正负样本采样，从而实现目标跟踪轨迹的实时更新，并对采样器进行更新坐标的实时反馈.通过实验室缩尺试验和野外实测对小车的视频跟踪精度进行了研究，结果表明，该方法有效避免了压缩感知目标跟踪算法存在的轨迹漂移情况，识别精度较传统压缩感知目标跟踪算法有显著提高.

1 卡尔曼滤波原理

卡尔曼滤波算法在系统中将目标从过去状态转移到当前状态的变换过程称为状态转移，其中包括了运动目标位置、速度、加速度等的转移，将本时刻获取的目标状态称为观测状态［18］.采用线性表达式表示该过程，并假设噪声干扰相互独立且满足高斯分布.根据卡尔曼滤波增益系数对状态转移后得到的新状态预测值和观测值进行加权计算，获得最终的目标状态值.

用于状态预测的卡尔曼滤波状态转移方程为：

目标观测方程为：

式中：xk∈Rn称为状态变量；zk∈Rm称为测量变量；ωk∈Rp称为系统中的噪声变量；vk∈Rm为测量中的噪声变量；Ak为转移状态矩阵；Hk为测量转移矩阵.

卡尔曼滤波计算步骤包括初始化滤波器、状态预测阶段、状态观测和状态更新阶段等四个步骤，卡尔曼滤波流程图如图1所示.

图1 卡尔曼滤波流程Fig.1 Flow chart of Kalman filter

滤波的初始阶段，主要内容包括对目标的初始位置、初速度、状态观察矩阵H、状态转移矩阵A、观察噪声协方差R、系统的噪声协方差Q等进行赋值.滤波预测阶段，主要为利用上一时刻运动状态去预测本时刻的目标运动状态，包括利用上一时刻状态变量值（或初始状态变量值）预测本时刻的状态变量值，利用上一时刻误差协方差值（或初始误差协方差值）预测本时刻的误差协方差值.其中，状态变量预测方程为：

误差协方差变量预测方程为：

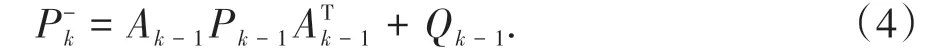
式中，设观测和测量噪声不相关，均满足高斯分布，方差矩阵为Qk、Rk.

状态更新阶段，使用卡尔曼滤波增益系数作为权重，综合考虑状态变量预测值和观测值跟绝对真实值的接近程度，取状态变量预测值与观测值的加权和作为最终的状态变量更新值.

卡尔曼滤波增益系数计算：

状态变量更新：

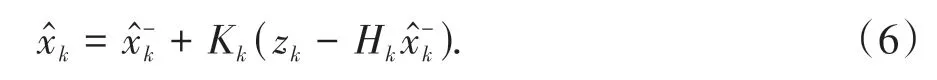
误差协方差值更新：

式中：I为单位矩阵.

2 压缩感知目标跟踪算法

利用压缩感知理论进行采样时，首先要确定目标区域，通过人工手动的方式框选特征区域并设置采样条件.提取图像前景的目标特征信息时，会减小样本区域外边界的搜索半径，减少算法的计算量，以便于算法在目标区域附近提取正样本；在提取背景目标特征时，特征采样将主要围绕内、外边界半径之间的环形区域进行.此外，设置一定的概率满足条件控制样本数量［19］.

针对目标跟踪任务中所存在的尺度变换问题，压缩感知理论通过选取具有多尺度的矩形滤波器｛ℎ1，1，…，ℎw，ℎ｝，用以实现对目标区域内的各样本进行卷积操作.所涉及到的矩形滤波器可表示为：

式中：i、j分别代表矩形滤波器的宽、高信息.

确定随机测量矩阵时，既要考虑计算的复杂程度，也需要依据目标特性来合理选取.根据研究文献的建议可知［20］，随机高斯矩阵常被用作压缩感知理论中的特定随机矩阵，其中各元素均满足N（0，1）分布.该理论可表达为：

式中：s表示计算复杂度，通常将其数值设置为4.

高维特征信息压缩方面，采样样本在与矩形滤波器进行卷积运算后，得到维度尺度处于106～1010范围内的高维特征向量X.此时，将随机测量矩阵R投影至低维特征向量V.其中，该过程无需考虑原始信号所可能产生的特征丢失问题.这一过程可表示为：

分类器更新设置方面，采用同一组滤波器，从而得到样本容量一致、各样本特征值具有多样性的数据集.依据所设置的不同类型样本，将所提取到的图像特征分为两组.其中，第Ⅰ组为前一帧中所提取到的前（背）景图像特征值，该样本用于对分类器进行权值更新.第Ⅱ组则为当前帧所提取到的图像特征值，通过分类器进行对象分类，进而利用Naive-Bayes 分类器对所得低维特征中的所有信息做处理［21］：

分类器H（v）中的条件分布概率应满足以下分布情况：

式中：μi1、σi1分别表示前景目标中第i个特征所对应的均值和标准差；μi0、σi0分别表示背景目标中第i个特征所对应的均值和标准差.

在实际跟踪时，在每一帧图像中进行分类器参数重置，从而实现对Naive-Bayes 分类器的权值更新.其中，所涉及的参数均值和方差的初始化过程可表示为：

3 基于卡尔曼滤波改进的压缩感知目标跟踪算法

传统压缩感知追踪算法，在目标跟踪过程中容易出现追踪漂移等情况，导致目标跟踪结果不稳定，具有较大的波动性.为实现精确的目标跟踪，本文提出了采用卡尔曼滤波技术改进的压缩感知目标追踪算法思路.利用Matlab 对已成熟的卡尔曼滤波技术与压缩感知技术进行融合，以达到提高跟踪精度以及改善跟踪漂移情况的目的.设计思路如图2 所示，首先，利用压缩感知跟踪算法的跟踪结果作为第k步的观测值，其次利用卡尔曼滤波预测第k步的预测值，最后利用卡尔曼滤波增益系数综合考虑观测值与预测值的可靠性，以观测值与预测值的加权和作为最终跟踪结果.卡尔曼滤波的原理是利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计.卡尔曼滤波可以应用于含有不确定信息的动态系统中，有效地抵抗噪声的干扰并对状态变量做出最优估计.在目标与背景或其他物体外观相似、噪声、遮挡等情况下会对运动目标的检测及特征提取造成困难，导致识别目标框可能与目标实际位置有所偏差即产生跟踪漂移.采用卡尔曼滤波的作用在于获得目标在下一帧中的预测信息，根据预测信息建立连续图像帧间的矩形框，进而通过目标信息匹配得到预测值，从而有效解决在较复杂情况下目标跟踪漂移的问题.

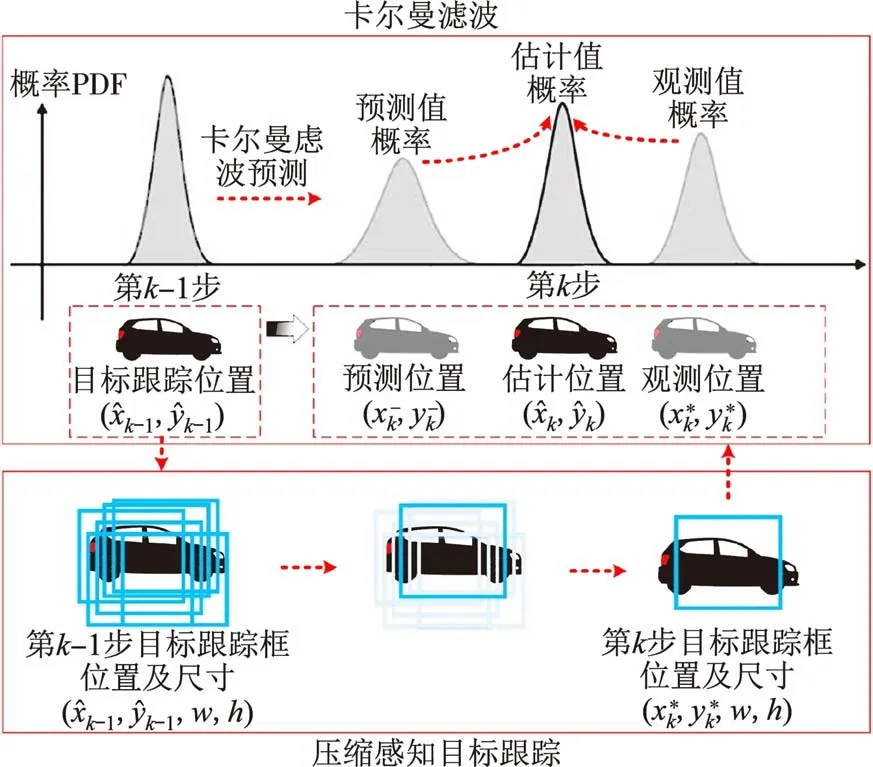
图2 基于卡尔曼滤波改进跟踪算法流程图Fig.2 Flow chart of the improved tracking algorithm based on Kalman filter

3.1 第一帧计算步骤

第一帧的计算目的在于手动框选跟踪目标并训练朴素贝叶斯分类器对于目标样本与背景样本的分辨能力，具体流程如图3所示，计算步骤如下.

二是末级渠系改善，节水效果明显。各项目区共完成末级渠系改造233km多，新建改建涵闸、农门、跌水、桥涵、分水口6 300多处，整治塘堰近200口，新建和改造量水设施583多处。斗农渠等末级渠系的灌溉水平均利用系数由原来的0.55提高到0.77。

图3 第一帧目标框坐标识别流程Fig.3 The recognition process of first frame for target frame coordinate

第一步，利用Matlab 将拍摄的车辆目标跟踪视频分解为逐帧的视频图像，并在视频第一帧用大小为｛x，y，w，h｝目标框框选目标跟踪对象，其中x、y分别为方形目标跟踪框左上角横、纵坐标值，w、h分别为跟踪框的宽度和高度.

第二步，根据第一帧（或上一帧）的目标框坐标及其尺度｛x，y，w，h｝，设置目标跟踪框内部的样本采样量，即跟踪目标采样量.设置采样半径和目标跟踪框外部的样本采样量，即背景采样量.其中，目标采样和背景采样也称之为正样本采样和负样本采样.最后再采用多尺度滤波器｛h1，1，…，hw，h｝，如式（8），对正负两个样本采样区域分别进行采样，形成更高维的特征向量进而组成特征向量x=｛x1，x2，…，xm｝，其中m=（wh）2.

第三步，根据式（9）和式（10），采用满足RIP 准则的观测矩阵，对采样范围内的多尺度正负样本区域采样的高维特征向量，进行随机投影，将高维度特征向量x降至低维度向量v，并按照式（12）计算v的μi1和σi1，μi0和σi0.

第四步，将计算的候选样本特征代入式（11），进行朴素贝叶斯分类计算，并取得H（v）最大时所对应的样本特征对应的目标特征为本帧跟踪目标的位置.

3.2 第二帧计算步骤

第二帧的计算目的在于利用压缩感知目标跟踪算法识别出第二帧的方形目标跟踪框的坐标，并结合第一帧手动确定的目标跟踪框坐标计算出第一帧到第二帧跟踪框坐标的变化速率，为接下来第k（k＞3）帧计算做准备，第二帧的具体流程如图4所示.

图4 第二帧目标框坐标识别流程Fig.4 The recognition process of second frame for target frame coordinate

计算步骤如下：

第一步，在上一帧目标中心采样半径r个像素区域进行正负样本采样.

第三步，在本帧目标位置处，重复第一步操作.其次，计算正样本的均值、方差μi1和σi1，计算负样本的均值和方差μi0和σi0.最后，根据式（13）更新均值和方差.

3.3 第三帧计算步骤

第一步，计算第一帧目标像素坐标（x1，y1）与第二帧目标像素坐标（x2，y2）的差值作为像素目标坐标在第一帧图像与第二帧图像间目标的变化速率，并近似将其作为第二帧至第三帧的变化速率：

式中：xi和yi分别为目标跟踪框左上角像素坐标x轴取值与y轴值.

第二步，在第二帧的像素坐标（x2，y2）与计算出的前两帧像素坐标变化速度（vx，2，vy，2）的基础上，利用卡尔曼滤波的状态转移公式（15）和（16）以及误差协方差变量预测公式（17）和（18）对下一时刻（帧）方形目标跟踪框左上角的坐标的状态变量和图像上方形目标跟踪框左上角像素坐标x轴与y轴的误差协方差矩阵进行预测.

第三步，在上一帧目标中心采样半径r个像素区域进行正负样本采样，并进行常规压缩感知目标跟踪算法步骤，识别出本帧目标的观测位置Z3.同时，利用上一帧方形目标跟踪框像素坐标（x2，y2）与本帧观测到的方形目标跟踪框（x3，y3）做差求（vx2，vy2），进而求出本帧图像中方形目标跟踪框像素坐标的状态变量观测值X3和Y3.

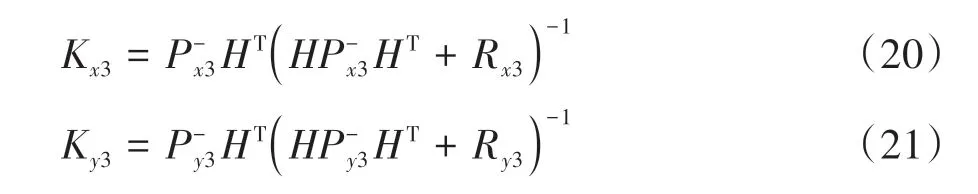
式中：H=［11］T为观测矩阵.

第六步，将卡尔曼滤波计算后的方形目标跟踪框左上角坐标值与跟踪框的长框尺度组合成最终的跟踪目标范围，并在该目标跟踪范围周围进行正负样本采样，计算正负样本特征以更新朴素贝叶斯分类器的分类参数，从而为后续的跟踪计算做准备.

3.4 第k(k＞3)帧计算步骤

首先在上一帧跟踪目标结果周围，进行正负样本采样；其次，利用多尺度滤波器计算样本特征，并利用压缩感知技术对样本特征进行压缩采样以降低后续计算量；最后利用朴素贝叶斯分类器对正负样本进行分类，确定本帧目标所在像素位置（xk，yk）.同时利用第k-1 步和第k-2 步跟踪结果计算第k-1 步到第k步像素坐标的变化速率，并将上述求解结果组成x轴和y轴的方形目标跟踪框对应的本时刻观测状态变量，如式（26）（27）计算：

后续卡尔曼滤波观测值修正步骤按式（28）～（35）计算，计算流程图如图5所示.

图5 后续第k帧目标框坐标识别Fig.5 Target box coordinate recognition in the subsequent k frame

数据预测：

数据更新：

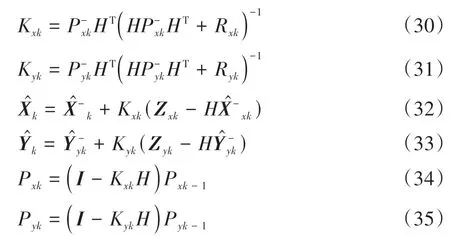
4 中心位置误差

为了验证后续的跟踪效果，本文将引入中心位置误差作为评判标准，其计算公式为［22］：

式中：O和O1分别代表真实目标区域中心和跟踪算法计算得出的目标区域中心.中心位置误差的大小反映了车辆跟踪的效果.

5 实验室试验测试

5.1 场景设置

针对本文提出的基于卡尔曼滤波改进型的压缩感知车辆目标跟踪方法（Kalman-CT），通过实验室缩尺模型跟踪试验验证其对缩尺车辆的跟踪有效性.为使测试结果满足实际需求，要求缩尺模型与真实对象在视觉外观上具有一定可比性.本文选用外形与真车相似度较高的缩尺仿真吉普车辆模型对实际车辆进行模拟，其车身长度约为30 cm，车身宽度约为15 cm，车身高度约为18 cm，车身重量约0.5 kg，如图6所示.

图6 测试所用车辆模型Fig.6 Vehicle model for testing

压缩感知目标跟踪算法采用计算跟踪目标的像素特征以及跟踪目标的背景像素特征，并采用朴素贝叶斯分类辨别方法进行跟踪目标的识别，所以背景环境颜色会影响压缩感知目标跟踪算法的跟踪精度.因此，本文在亚克力塑料模型桥上铺设了灰色卡纸模拟真实背景桥面的沥青混凝土路面，如图7所示.

试验过程中，采用Canon 5D Mark IV 摄像机对模型车辆进行拍摄，设置其视频分辨率为1 920×1 080 P/60 fps.相机通过三脚架连接并固定在独立于桥梁模型的减速平台，防止车辆行驶过程中产生的抖动造成视频拍摄效果成像晃动、相机失稳等情况出现.同时，相机离地保持一定高度，确保摄像机视频拍摄内容包含车辆在桥面行驶的全过程.

5.2 试验测试

本文采用两条白色方形PVC塑料方管作为轨道边缘约束，进而模拟车辆行驶轨迹.首先，采用人工推动的方式，使车辆做减速运动、缓慢经过桥面，并用架设的Canon 5D Mark IV 摄像机对模型车辆进行拍摄，将拍摄的车辆运动视频分解为按增序排列的视频帧图像；其次，选取视频帧的第一帧图像，确定跟踪目标所在的像素区域并设置坐标和尺度合适的目标跟踪框，如图7 所示，预设目标框参数｛x，y，w，h｝=｛2 760，990，512，468｝；最后，利用压缩感知目标跟踪算法，在第一帧（上一帧）图像中计算的跟踪目标附近进行扩大搜索，并计算扩大区域的像素特征，利用第一帧（上一帧）图像中计算的跟踪目标像素特征与背景像素特征的分类器对本帧图像的像素特征进行分类识别，确定跟踪目标可能存在的像素区域.

5.3 采用CT跟踪结果更新分类器

如图8所示，首先，采用CT的跟踪结果更新朴素贝叶斯分类器，以下简称CT-I；其次，采用卡尔曼滤波修正每次CT的跟踪结果，以下简称Kalman-CT-I；最后，对比修正前后的跟踪结果，如图9 所示.相较于CT-I，Kalman-CT-I 使得跟踪结果的平均误差降低了23%，最大误差降低了77%.采用Kalman-CT-I可以较为有效地避免跟踪漂移问题，跟踪路径更加趋近真实值.

图8 分类器更新方式ⅠFig.8 Classifier update method Ⅰ

图9 实验室目标跟踪结果ⅠFig.9 Laboratory target tracking results Ⅰ

5.4 采用卡尔曼滤波修正后的CT 跟踪结果更新分类器

如图10 所示，首先，采用卡尔曼滤波修正每次CT 的跟踪结果，以下简称CT-Ⅱ；其次，利用修正后的跟踪结果更新朴素贝叶斯分类器，以下简称Kalman-CT-Ⅱ；最后，对修正前后的跟踪结果进行对比，如图11 所示.相较于CT-Ⅱ，Kalman-CT-Ⅱ使得跟踪结果的平均误差降低了28%，最大误差降低了60%.每帧确定的CT-Ⅱ计算坐标和Kalman-CT-Ⅱ修正坐标轨迹趋于重合，说明卡尔曼滤波不仅能够修正每帧中的CT-Ⅱ计算结果，还能使后续帧的CT-Ⅱ跟踪结果趋近卡尔曼滤波算法的预测结果.在跟踪起始Kalman-CT-Ⅱ明显改善了CT-Ⅱ跟踪结果漂移的情况，Kalman-CT-Ⅱ跟踪轨迹精度相较于CT-Ⅱ算法有较大提升.

图10 分类器更新方式ⅡFig.10 Classifier update method Ⅱ

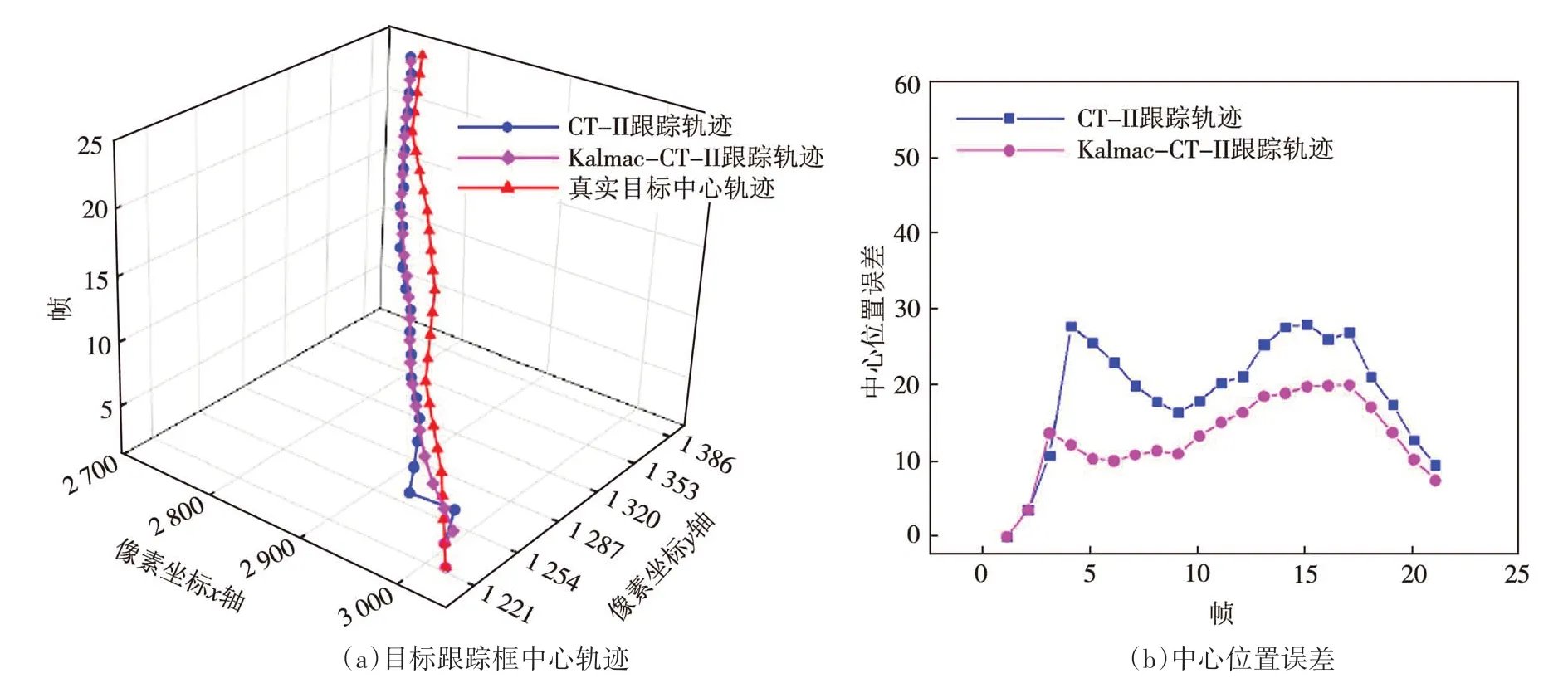
图11 实验室目标跟踪结果ⅡFig.11 Laboratory target tracking results Ⅱ

5.5 跟踪结果对比分析

对比CT-Ⅰ跟踪结果与Kalman-CT-Ⅱ跟踪结果，如图12 所示.相较于CT-Ⅰ，Kalman-CT-Ⅱ使得跟踪结果的平均误差降低了48%，最大误差降低了75%.Kalman-CT-Ⅱ相较于CT-Ⅰ得到的跟踪轨迹更加平稳光滑，跟踪轨迹更趋近车辆真实运动轨迹，改善了轨迹漂移情况，且跟踪轨迹误差明显降低.

图12 实验室目标跟踪结果对比Fig.12 Comparison of laboratory target tracking results

6 野外试验测试

野外试验测试过程中，车辆从右侧道路驶入，并左转90°从左侧道路驶出，车速大致是20 km/h.首先，将摄像机架设于人行道处，对车流进行拍摄，并将拍摄的车辆运动视频分解为按增序排列的视频帧图像；其次，选取视频帧中的第一帧图像，确定首帧目标坐标和合适跟踪框尺度；最后，设置相关跟踪参数进行跟踪计算，预设目标框参数｛x，y，w，h｝=｛1 267，435，334，180｝.同时，为了研究卡尔曼滤波的修正效果，本文分别讨论了采用CT 的跟踪结果更新分类器和采用Kalman-CT 跟踪算法的跟踪结果更新分类器后，车辆目标的跟踪结果及其精度.

6.1 采用CT算法跟踪结果更新分类器

采用图8 分类器更新方式Ⅰ进行车辆目标跟踪，将卡尔曼滤波修正前后的跟踪结果进行对比，如图13所示.相较于CT-Ⅰ，Kalman-CT-Ⅰ使得跟踪结果的平均误差降低了25%，最大误差降低了78%.采用卡尔曼滤波算法修正跟踪结果后，跟踪路径更趋近真实值.

图13 野外目标跟踪结果ⅠFig.13 Field target tracking results Ⅰ

6.2 采用卡尔曼滤波修正后的CT 跟踪结果更新分类器

采用图10 分类器更新方式Ⅱ进行车辆目标跟踪，如图14 所示.相较于CT-Ⅱ，Kalman-CT-Ⅱ使得跟踪结果的平均误差降低了72%，最大误差降低了96%.对比修正前后的跟踪结果发现传统CT 算法（CT-Ⅱ）的跟踪结果存在较大的漂移，而采用卡尔曼滤波算法修正后的跟踪算法（Kalman-CT-Ⅱ）有效避免了轨迹漂移，运动轨迹更加光滑，符合实际的车辆行驶情况.

图14 野外目标跟踪结果ⅡFig.14 Field target tracking results Ⅱ

6.3 跟踪结果对比分析

将CT-Ⅰ跟踪算法计算结果与Kalman-CT-Ⅱ跟踪算法计算结果进行对比，如图15所示.相较于CT-Ⅰ，Kalman-CT-Ⅱ使得跟踪结果的平均误差降低了89%，最大误差降低了99%.Kalman-CT-Ⅱ跟踪算法可以更加稳定地跟踪车辆目标，且跟踪误差较CT-Ⅰ显著降低，跟踪轨迹更加符合实际车辆行驶情况.