矩形钢管偏心相贯梁柱节点平面内抗弯承载力
2023-01-31郭小农徐泽宇刘俊罗金辉
郭小农,徐泽宇,刘俊,罗金辉
(同济大学 土木工程学院,上海 200092)
相贯节点具有构造简单、施工便捷、传力直接的优点,是钢管结构中最具代表性的节点构造[1].迄今为止国内外对于各类型相贯节点承载性能的研究已较为系统[2-5]并形成相关规范[6-7],例如分析节点静力特性的塑性铰线模型[8]以及分析节点疲劳特性的热点应力法[9].由于相贯节点的无加劲构造常使其表现出明显的半刚性连接特性,故对于节点刚度对整体结构影响的研究也较完整[10-11].
近年来,相贯节点除被应用于体育馆等空间结构外,以矩形钢管作为梁柱构件、梁柱节点采用相贯节点的框架结构在装配式建筑,尤其是室外电梯井等结构中的应用逐渐推广.而偏心相贯节点由于梁柱构件轴线异面垂直,外侧腹板平齐,使建筑外表面平整、具有更好的美学效果及空间利用率,
相较于传统的中心相贯节点,偏心相贯节点可有效提高节点的力学性能,故其使用也开始得到重视.目前国内已有偏心相贯节点的应用案例,如上海世博会西班牙馆[12],但对于矩形钢管偏心相贯节点的研究较少,仅赵必大等[8,11]对该节点平面外承载力及刚度进行了系统的研究.
本文针对矩形管偏心相贯节点在框架结构中的应用开展研究,完成了柱在一定轴压比下、梁受平面内弯矩作用的抗弯承载性能试验,并探究外加劲肋对于节点性能的影响,补充了在相贯节点外加劲形式方面研究的不足.通过建立数值模型进行参数化分析,最终拟合得到矩形钢管偏心相贯节点在平面内的抗弯承载力计算公式.
1 偏心相贯梁柱节点试验
1.1 试件设计
试验所用节点形式为T 形偏心方管相贯节点,柱构件为方管(截面□200 mm×200 mm×8 mm),梁构件为矩形管截面(□250 mm×150 mm×6 mm),节点构造和尺寸参数如图1 所示,构件尺寸与实际工程保持一致.节点构造分为无加劲肋和有加劲肋两种形式,无加劲肋节点中梁和柱外缘对齐,采用E50 型焊条全熔透对接焊.有加劲肋节点在无加劲肋节点构造的基础上,将厚度为6 mm 的加劲板置于梁上下翼缘处,与梁和柱焊接.为安装加劲肋,节点设有一段200 mm 的平面外梁段,加劲肋在沿梁方向上的长度为120 mm.试验完成无加劲肋节点及有加劲肋节点各一件,所有构件的材料均选用Q345,在梁柱构件上取样并加工标准材料拉伸试件6 根,材性试验结果如表1所示.

图1 节点构造示意图(单位:mm)Fig.1 Schematic diagrams of joints(unit:mm)
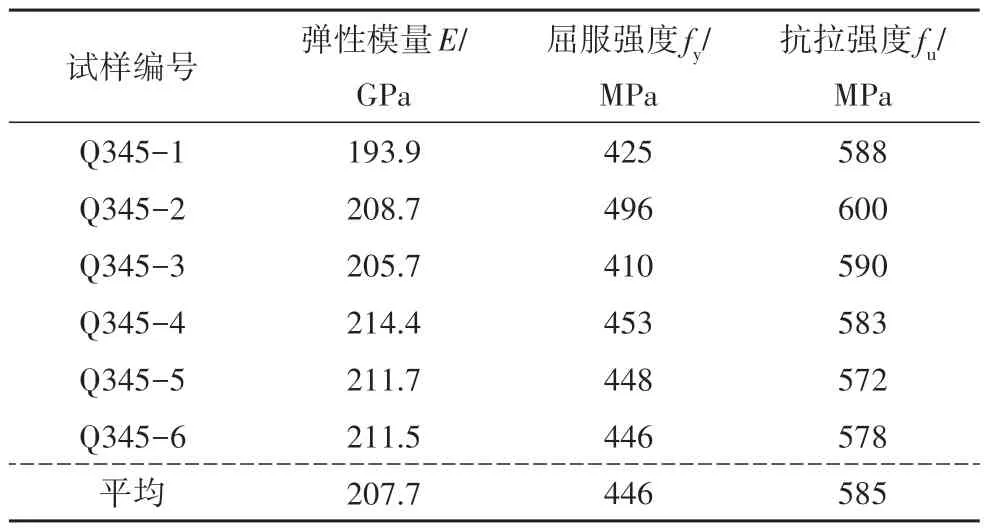
表1 材性试验结果Tab.1 Result of the material property test
1.2 加载方案
加载装置如图2 所示,采用了两个竖向反力架和一个水平反力架进行加载,柱构件长1.6 m,梁构件长1.1 m,加载点距离柱轴线1.45 m.柱底支座采用螺栓固接,柱顶支座仅释放平面内转动自由度及竖向平动自由度,加载端为铰接.为模拟节点在框架结构中的实际受力情况,首先在柱顶按三级进行竖向加载,每级为200 kN,然后维持600 kN 轴力不变,使柱子的轴压比维持为0.25;梁端选用20 t千斤顶施加单调荷载,加载方向平行于柱轴线,逐级加载直至节点破坏,每一级按照节点预测极限承载力的5%进行加载,加载达到每一级预定承载力时停留充足时间.

图2 加载方案示意(单位:mm)Fig.2 Loading scheme(unit:mm)
1.3 测点布置
测点布置如图3 所示.位移计D1~D2、D14~D15用于测量柱转角;D3~D6 以及D13 用于测量梁挠度;D11、D12 用于测量梁出平面的变形情况;D16、D17用于测量支座转动;在梁根部也伸出四根短杆通过测量其沿梁轴线方向的位移(D7~D10)来得到柱面板的变形.

图3 测点布置图(单位:mm)Fig.3 The arrangement diagram of monitoring points(unit:mm)
杆件外表面布置单向应变片,柱构件上位置为距离梁翼缘板各300 mm 处截面(S1~S8),梁构件上位置为距离梁根部125 mm 处截面(S9~S10、S15~S16),每个截面布置4 个应变片,主要用于校核荷载并评估荷载是否偏心.由于偏心节点两侧受力分布不均,故腹板上增设4 个应变片(S11~S14)用于更准确地测量梁上的应力分布.节点域应力复杂,故采用三向应变花,柱构件上布置8枚,编号为T1~T8,梁构件上布置4枚,标号为T9~T12.对于有加劲肋节点,于加劲肋处增设三向应变花4枚,编号T13~T16.
1.4 试验结果
对于无加劲肋节点,节点加载初期,弯矩-转角曲线近似保持直线,节点域保持弹性,之后偏心一侧柱腹板发生鼓曲变形,节点刚度出现明显下降;当节点所受弯矩接近极限承载力时,柱腹板出现明显鼓曲变形,柱翼缘板产生凹陷变形,如图4(a)(b)所示;此时采用位移加载,节点在较大变形情况下承载力未出现明显下降.节点的最终破坏模式为柱翼缘板屈服与腹板压屈的组合破坏.
对于有加劲肋节点,节点加载初期,节点域仍保持弹性,管壁变形并不显著,加劲肋最先产生可见的屈曲变形,之后节点刚度出现明显下降;当节点所受弯矩接近极限承载力时,柱腹板出现明显鼓曲变形,柱翼缘板产生凹陷变形,此时加劲肋屈曲变形严重,如图4(c)所示.节点受力末期,加劲肋屈曲,丧失继续承载的能力,此时受力形式与无加劲肋节点相同,故最终破坏模式也为柱翼缘板屈服与腹板压曲的组合破坏.

图4 试件典型破坏模式Fig.4 Typical failure model of test specimens
试验结果表明,节点主要发生3 种破坏模式,如图4 所示.无加劲肋节点为柱腹板的鼓曲变形,见图4(a),柱翼缘板的弯曲凹陷变形见图4(b),有加劲肋节点还会发生加劲肋的屈曲变形,见图4(c).由于相贯节点的变形主要集中在支管和主管连接处,节点域可视作刚域,故可采用如图5 所示的简化力学模型[13].偏心相贯节点的面板凹陷变形与侧板上的局部拉压变形也集中在面板处,故可采用同样的力学模型,节点的弯矩和转角可取梁柱连接面处的数值.实际工程中,节点域刚度EI为常数,而位移计D13的读数Δmi由两部分组成[14-15]:1)杆件弯曲变形引起的挠度Δi;2)节点变形引起的位移δi,如图6所示.因此节点转角可按式(1)计算.

图5 相贯节点力学模型Fig.5 The mechanical model of the welded joint

图6 试件变形示意Fig.6 Diagram of deformation

式中:Δmi为在节点域刚度无穷大时位移计D13 处的竖向位移值,采用数值计算方法获得;lw为加载点至梁柱连接面处的距离.最终采用图5 所示的力学模型,根据实测数据计算得到的两种相贯节点的弯矩转角曲线如图7所示.
从图7 可以看出,随着荷载增大,变形不断增加,但在较长范围内不会出现荷载的极值点.受制于试验条件,加载末期梁端已发生很大变形,实测加载端竖向变形已大于60 mm,大于加载梁长度的1/20,梁柱节点转角也大于0.03 rad,此时仍未出现极值点,故停止加载.对于相贯节点的极限承载力一般按变形准则确定[16-17],变形值一般取为3%的主管宽度.当节点面板的相对变形达到极限变形0.03B=6 mm 时,梁高为h=250 mm,节点转角φ≈0.03B/h=0.024 rad,故对试验节点可取φ=0.024 rad 时对应的弯矩作为极限弯矩Mu.无加劲肋偏心相贯节点的极限承载力为95.41 kN·m,有加劲肋偏心相贯节点的极限承载力为126.24 kN·m,加劲肋可以显著提高节点的承载力.

图7 弯矩-转角曲线Fig.7 Moment-rotation curves
2 数值模型的建立和验证
2.1 数值模型
采用通用有限元软件ABAQUS 对矩形钢管偏心相贯节点进行数值模拟,节点有限元模型如图8 所示.所有构件,加劲肋及焊缝均采用三维线性减缩积分六面体单元(C3D8R)模拟,节点域及梁柱焊缝交接处采用更细致的网格,厚度方向划分为4 层,节点域网格划分如图8(b)(c)所示.材料本构采用双线性强化模型,根据材性试验结果取真实应力应变,fy=450 MPa,fu=650 MPa,弹性模量E=2.08×105MPa,切线模量E′=0.005E,泊松比ν=0.3.由于节点为静力加载,且焊缝与钢材等强设计,焊缝材性对于节点整体性能影响较小,故焊缝也采用双线性强化模型建模.有限元模型支座约束条件与试验相同,在端部截面形心处设置参考点(RP 点),并在RP 点上施加约束及荷载.其中,柱底端约束全部自由度;柱顶端仅释放平面内转动自由度及竖向平动自由度;柱顶端持续施加600 kN集中力;梁端的加载制度与试验相同,逐级进行单调加载.梁柱构件通过焊缝相连,故焊缝与构件的连接面均采用绑定约束.

图8 节点有限元模型Fig.8 The finite element model of the joints
2.2 节点破坏模式
图9 给出了两种矩形管偏心相贯节点的典型破坏模式图.对于无加劲肋偏心相贯节点,塑性区主要在与梁连接的柱翼缘及柱腹板上开展,故主要发生柱翼缘板的凹陷变形以及柱腹板的鼓曲变形.主管和支管不等宽的中心相贯节点的受力机理是通过主管面板的抗弯来传递支管的轴力和弯矩,主要发生主管面板的凹陷变形;主管和支管等宽的中心相贯节点的受力机理是通过主管腹板的面内受力来传递支管的轴力和弯矩,主要发生主管腹板的鼓曲变形.而对于本文所研究的一侧平齐的偏心相贯节点,其受力机理是上述二者的组合.对于有加劲肋偏心相贯节点,加劲肋首先进入全截面屈服并发生屈曲,随后节点的受力机制与无加劲肋节点相同,柱翼缘板与腹板的最终变形情况与无加劲肋节点几乎一致.对比图4和图9可知,有限元模型可以精确地模拟出和试验现象一致的破坏模式.

图9 有限元分析结果Fig.9 Numerical results
2.3 弯矩-转角曲线
图10 给出了两种节点的弯矩-转角曲线的数值分析结果与试验结果的对比.可以看出有限元模型在全程都能较好地模拟试验结果.表2 给出了节点的极限弯矩试验结果与有限元结果的对比,从表2可知,对于无加劲肋相贯节点,极限弯矩Mu的试验实测结果与有限元计算结果之间的误差为0.98%;对于有加劲肋相贯节点,极限弯矩Mu的试验实测结果与有限元计算结果之间的误差为-0.26%,表明有限元模型具有足够的精度.

图10 试验及有限元弯矩-转角曲线Fig.10 Bending moment-rotation curves of experimental and numerical results

表2 试验与有限元结果对比Tab.2 Comparison between experiential and numerical results
2.4 与普通相贯节点比较
使用相同的建模方式以柱构件□200 mm×200 mm×8 mm、梁构件□250 mm×150 mm×6 mm 为例,建立普通相贯节点模型与偏心相贯节点模型并进行对比,两种节点弯矩-转角曲线如图11 所示.取φ=0.024 rad 时对应的弯矩作为节点极限弯矩,偏心相贯节点极限弯矩为75.58 kN·m.普通相贯节点极限弯矩为53.24 kN·m,我国规范以及欧洲规范[6-7]计算结果均为51.89 kN·m,承载力计算误差为2.5%,证明了有限元模型建模方式的合理性和有效性.偏心相贯节点具有更高的承载力与初始转动刚度,以现有规范公式计算相同构件截面的偏心相贯节点承载力时会出现较大误差,所以需重新建立并拟合针对偏心相贯节点的承载力计算公式.

图11 弯矩-转角曲线比较Fig.11 Comparison of bending moment-rotation curves
3 参数分析和公式拟合
3.1 数值计算结果汇总
本文建立60 个数值模型,通过改变梁柱截面尺寸参数以研究尺寸规格对于矩形管偏心相贯节点承载性能的影响规律.确定节点形状的几何参数选择梁柱翼缘宽度比β(b/B)、梁截面高度与柱翼缘宽度比η(h/B)、柱截面管壁宽厚比γ(B/2T)、梁柱截面壁厚比τ(t/T),各参数意义如图1 所示.由于常用柱截面为方管,取柱截面宽度与高度相等.所有数值模型的建模信息详见表3.表4 中列出了各模型的极限承载力.模型按“J-P-p1-p2”进行命名,其中P 表示该组模型研究的参数,p1表示该组模型柱构件的宽度,p2表示构件尺寸变化的具体数值.

表3 数值模型参数汇总表Tab.3 Parameters of FE models

表4 有限元结果汇总表Tab.4 Numerical results
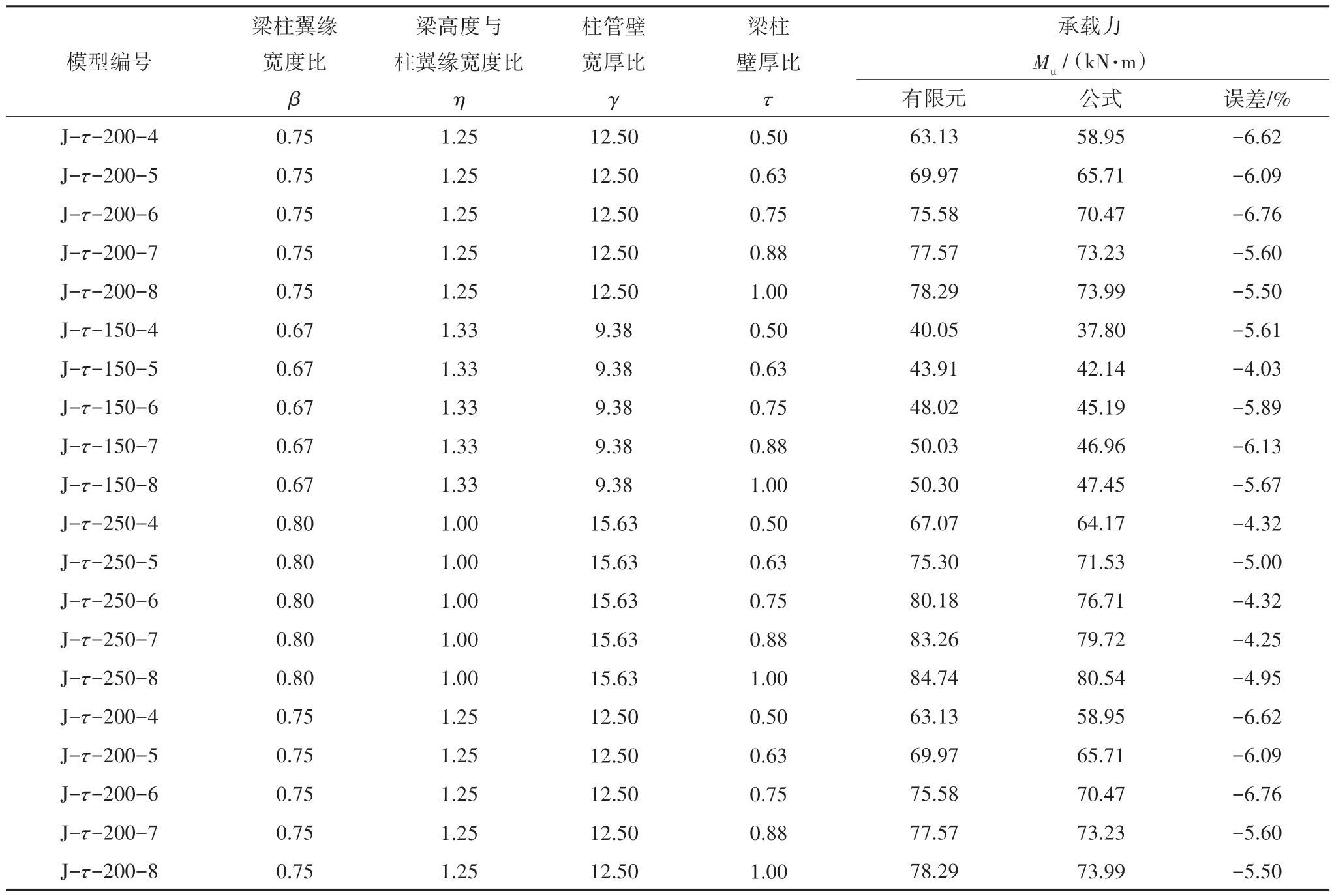
续表4
3.2 各参数的影响规律
在进行参数化分析时,考虑到实际工程中矩形管截面高宽比适用范围(0.5~2.0)[11]、屈服线模型适用范围(0.25≤β≤0.85)[16],以及偏心相贯节点自身构造特点,参数变化范围取0.5≤β≤0.85,1≤η≤2,7.5≤γ≤20,0.5≤τ≤1.
由图12 可知,极限承载力Mu与梁柱翼缘宽度比β、梁截面高度与柱翼缘宽度比η之间呈线性函数关系.在同样壁厚条件下,增大梁截面的高度和宽度可以提高节点承载力,且增大梁截面高度对提高节点承载力的效果更加显著.极限承载力Mu与柱截面管壁宽厚比γ、梁柱截面壁厚比τ之间呈非线性函数关系.在同样截面大小条件下,增大梁柱壁厚可以提高节点承载力,增大柱壁厚对于承载力的提高最为显著.当梁壁厚与柱壁厚相等时,再提高梁壁厚已经不能有效提高节点承载力.

图12 不同参数对节点极限承载力Mu的影响Fig.12 Effect of different parameters on Mu
3.3 承载力公式
由试验以及有限元结果可知,当节点达到极限变形时,柱腹板及翼缘板均发生了较大变形,故节点的抗弯承载力需考虑两者的共同作用.在欧洲规范[6]中基于薄壳理论以及塑性绞线法[18],T形方管相贯节点受弯承载力的计算公式如式(2)(3)所示,其中弦杆表面破坏对应柱翼缘板的凹陷变形,腹板屈曲破坏对应柱腹板的鼓曲变形.
破坏模式为弦杆表面破坏时,0.5≤β≤0.85,计算式为:

破坏模式为腹板屈曲破坏时,0.85≤β≤1,计算式为:

式中:fy为钢材屈服强度;T为柱构件壁厚;h为梁构件高度;β为梁柱翼缘宽度比;η梁截面高度与柱翼缘宽度比.
考虑矩形管偏心相贯节点极限承载力时可将节点承载力沿柱轴线分为两部分进行考虑,认为柱侧板一侧承载力发挥充分,等于破坏模式为腹板屈曲破坏时的承载力的一半,另一侧面板所能提供的承载力用系数k1加以考虑,并使用修正后的梁柱翼缘宽度比β*=(2b-B)/B进行计算.由于式(2)(3)在计算最终节点抗弯承载力时均未考虑梁柱截面壁厚比τ对节点承载力的影响,故引入系数k2加以考虑.最终节点承载力计算公式如式(4)所示.
有限元结果如图13 所示,可知当梁柱翼缘宽度比修正值β*小于0.5 时,系数k1随β*的增大呈非线性增大;当β*大于0.5 时,β*的改变对k1不再造成影响.对于梁截面高度与柱翼缘宽度比η,随着节点承载力的整体变小,节点承载力的分配规律发生变化.系数k1取得极值点时所对应的η值不断变大,出现当B=150 mm 时系数k1随η的增大先增大再减小的趋势,故使用二次函数可以较好地拟合出该规律;系数k1随柱截面管壁宽厚比γ呈线性函数关系,并随γ的增大而增大,故参数k1可写作式(5)的形式,当β*大于0.5时,取β*=0.5计算k1数值.系数k2随梁柱截面壁厚比τ的增大呈非线性增大,且对于所有节点其变化规律趋同,随着τ接近于1,k2不再发生变化,故参数k2可写作式(6)的形式.


图13 有限元结果(承载力)Fig.13 Numerical results(bearing capacity)
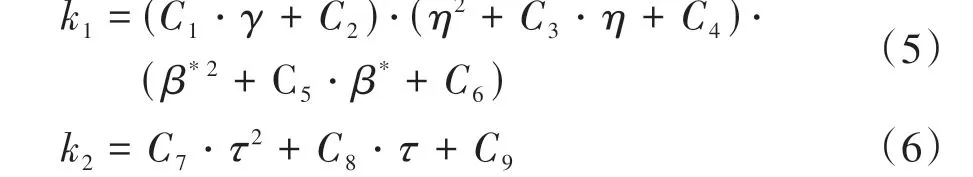
最终通过多元非线性回归分析[19]确定常系数C1~C9,节点抗弯承载力可按式(4)、式(7)、式(8)计算.利用有限元计算结果来校验参数化计算式,校验结果见表4,最大误差Δmax=-11.13%,平均误差Δavg=-5.30%,可较好地反映节点的平面内抗弯承载特性.

4 加劲肋对于节点性能的影响
4.1 数值计算结果汇总
目前相贯节点对于外加劲加强方法的研究工作较为有限.然而这种方法既可用于节点施工阶段,也可用于事后加固,对加工精度要求较低,具有良好的应用前景,因此本节针对外加劲肋对于偏心相贯节点性能的提高效果进行了系统的研究.
为考虑外加劲肋对于节点性能的有利影响,本文补充建立了50 个带加劲肋数值模型,通过改变梁柱构件及加劲肋尺寸以研究其对于节点承载性能的影响规律.确定节点形状的几何参数与无加劲肋节点一致,并考虑加劲肋厚度tl及加劲肋沿梁长度l对节点性能的影响.所有数值模型的建模信息及其极限承载力如表5所示.

表5 有限元结果汇总表Tab.5 Numerical results

续表5
4.2 承载力公式
由带加劲肋偏心相贯节点的试验及有限元结果可知,外加劲肋的存在相当于变相提高了梁截面宽度,使节点弯矩可以均匀分配至两侧腹板,故能有效提高节点承载力及刚度.加劲肋对于节点承载力的提高作用可以用式(9)表示,tl·l对应加劲肋的板件截面面积,h表示上下两块加劲板提供弯矩的力臂,fy为钢材屈服强度,系数α主要与节点几何形状有关,可以利用表征节点几何特性的无量纲数β*、η、γ、τ进行拟合.

对加劲肋几何参数tl、h、l的参数分析如图14 所示,节点承载力增量ΔMu与加劲肋板厚tl、梁高h、加劲肋沿梁长度l均成正比.对无量纲数β*、η、γ、τ的参数分析如图15 所示,可以发现系数α随梁柱翼缘宽度比修正值β*的增加呈线性增加,改变梁宽会改变加劲肋形状,从而影响ΔMu;梁截面高度与柱翼缘宽度比η、柱截面管壁宽厚比γ的改变对α影响较小,增加梁高或者加大柱壁厚不影响加劲肋形状,对ΔMu无影响;梁柱截面壁厚比τ对于带加劲肋节点性能的影响与不带加劲肋节点性能的影响相同,故在进行不带加劲肋节点承载力计算时已考虑其影响.最终拟合结果如式(10)所示,按式(4)及式(10)计算带加劲肋节点承载力并利用有限元计算结果来校验参数化计算式,校验结果如表5 所示,最大误差Δmax=6.28%,平均误差Δavg=0.43%,证明该计算式可以对节点承载力进行可靠的估计.表6 给出了偏心相贯节点试验结果与使用式(4)及式(10)公式计算结果的对比,公式计算结果的误差均小于5%,证明了公式的准确性.

图14 不同参数对节点极限承载力增量ΔMu的影响Fig.14 Effect of different parameters on ΔMu
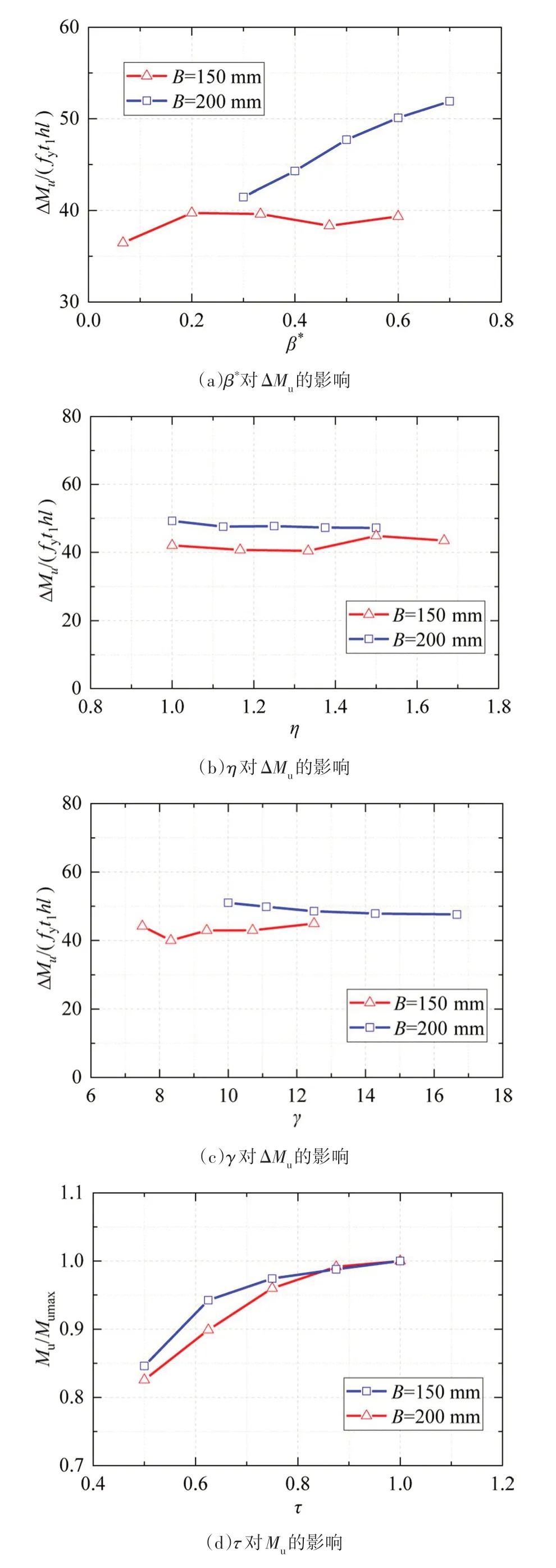
图15 有限元结果(承载力)Fig.15 Numerical results(bearing capacity)

表6 试验与有限元结果对比Tab.6 Comparison of the theoretical results with the test results
5 结 论
1)试验及有限元结果表明矩形管偏心相贯梁柱节点破坏模式为柱翼缘板屈服与腹板压曲的组合变形破坏.
2)节点平面内抗弯承载力Mu主要与梁截面高度与柱翼缘宽度比η以及柱截面管壁宽厚比γ有关,增大梁高h以及增大柱壁厚T对于承载力的提高最为有效.
3)加劲肋可以有效提高平面内抗弯承载力Mu,其性能主要与加劲板尺寸有关,受梁柱构件几何尺寸影响较小.
4)试验和有限元结果验证了矩形管偏心相贯梁柱节点平面内抗弯承载力Mu计算式的准确性,当参数变化范围在0.5≤β≤0.85、1≤η≤2、7.5≤γ≤20、0.5≤τ≤1时,计算式的精度较高.
