构造形式对复合叠合板弯曲刚度的影响
2023-01-31罗斌
罗斌
(兰州理工大学 土木工程学院,甘肃 兰州 730050)
随着我国政府层面推广装配式建筑力度的不断加大[1],混凝土叠合板作为装配整体式混凝土结构的重要部品构件,因具有整体性好、施工速度快、节约模板、可大幅提升建筑预制率与装配率等优点[2],受到工程界与学术界的广泛关注.与此同时,由于人们对居住功能要求的日益提高,便于功能分割的大开间住宅(6~8 m)逐渐成为民用建筑的发展趋势[3],而实现灵活大开间住宅的关键技术则是大跨度楼板,因此研发适用于民用住宅建筑领域的大跨度混凝土叠合板是未来装配式混凝土结构发展的方向.
在不改变混凝土材料的前提下,利用内置轻质芯材在楼板中性轴附近弯曲应力较小的部位形成空心或空腔的夹芯板、空心板,由于具有构件自重轻、刚度大等优点,是实现大跨度楼板的优异构造形式[4].然而,混凝土叠合板是预制与现浇工艺的结合.若将具有自重轻、刚度大等优点的夹芯板、空心板构造形式用于叠合板中,不仅需要其部品构件内部具有一定的空心率,而且还要具备保证新老混凝土良好传力性能的叠合面[5].为此,Rahman 等[6],Baran[7]及Ibrahim 等[8]将空心化技术应用在预制底板中,并通过试验及理论分析的方法提出了预制空心叠合板.但这类部品构件由于将空心化技术应用在预制底板中,无法有效降低后浇混凝土层的厚度,因此其组成的叠合板往往存在板厚度较大等缺点.
随后,学者们[9-11]又相继提出多种形式的后置内膜式预制混凝土空心叠合板(即在施工现场,待预制实心混凝土底板吊装至指定位置后,再在预制底板上铺设轻质内模芯材,最后浇筑后浇混凝土层而形成的预制混凝土空心叠合板).但这类叠合板构件由于将轻质内模芯材布置在后浇混凝土层中,尽管降低了后浇混凝土层的厚度,避免了所组成叠合板较大的板厚,但其轻质内模芯材采用后置铺设方法,降低了施工速度,无法体现装配式技术的先进性.
针对上述问题,结合课题组前期对装配式复合墙(由截面较小的钢筋混凝土肋梁、肋柱及内置蒸压加气混凝土砌块组成)的研发及推广应用[12],本次课题组将蒸压加气混凝土砌块(以下简称“加气块”)用于叠合板中,提出一种内填加气块的复合叠合板(以下简称“复合叠合板”),开展了不同参数变化(纵肋间距、加气块位置、是否存在横肋)的复合叠合板与现浇普通混凝土板受弯性能对比试验,分别从承载能力、弯曲刚度、截面整体工作性能等影响受弯性能的力学指标参数开展研究,对比分析了常规现浇板与复合叠合板受弯性能的异同;在此基础上,重点研究了不同参数变化对复合叠合板弯曲刚度的影响机理;依据影响主次因素,分别提出了适宜于不同受力阶段及不同构造形式的叠合板短期弯曲刚度计算公式,得到的数据和结论可为该类叠合板后续定型化研究及推广应用提供参考.
1 试验概况
1.1 试件设计
共设计了5 块单向板试件,试件基本参数见表1.LS-1~ LS-4 为本次提出的复合叠合板试件,LS-5为用于对比的普通现浇板.4块复合叠合板中加气块采用A3.5级;LS-5与4块复合叠合板(预制底板及后浇混凝土层)混凝土均采用普通C30 级.4 块复合叠合板的预制底板及LS-5 的底部纵向受拉钢筋均采用12@150,并采用6@200 的横向分布钢筋;LS-1~LS-3 的后浇层及LS-5 的顶部分别配置10@150的纵向受拉钢筋及6@300 的横向分布钢筋;为防止LS-1、LS-2 及LS-4 中横肋素混凝土在加载前开裂,在其横肋上、下各设置了2 根6 的构造钢筋;4块复合叠合板纵肋中的桁架钢筋采用B140型[13].

表1 试件基本参数Tab.1 Basic parameters of specimens
本文所提复合叠合板构造见图1;4 块用于试验的复合叠合板具体构造形式及配筋详见图2.
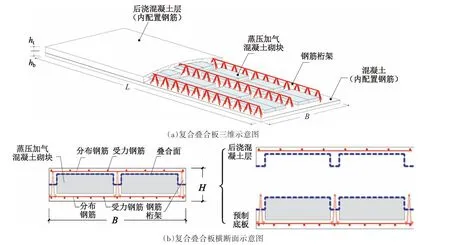
图1 复合叠合板构造示意图Fig.1 Shape diagram of of CCS
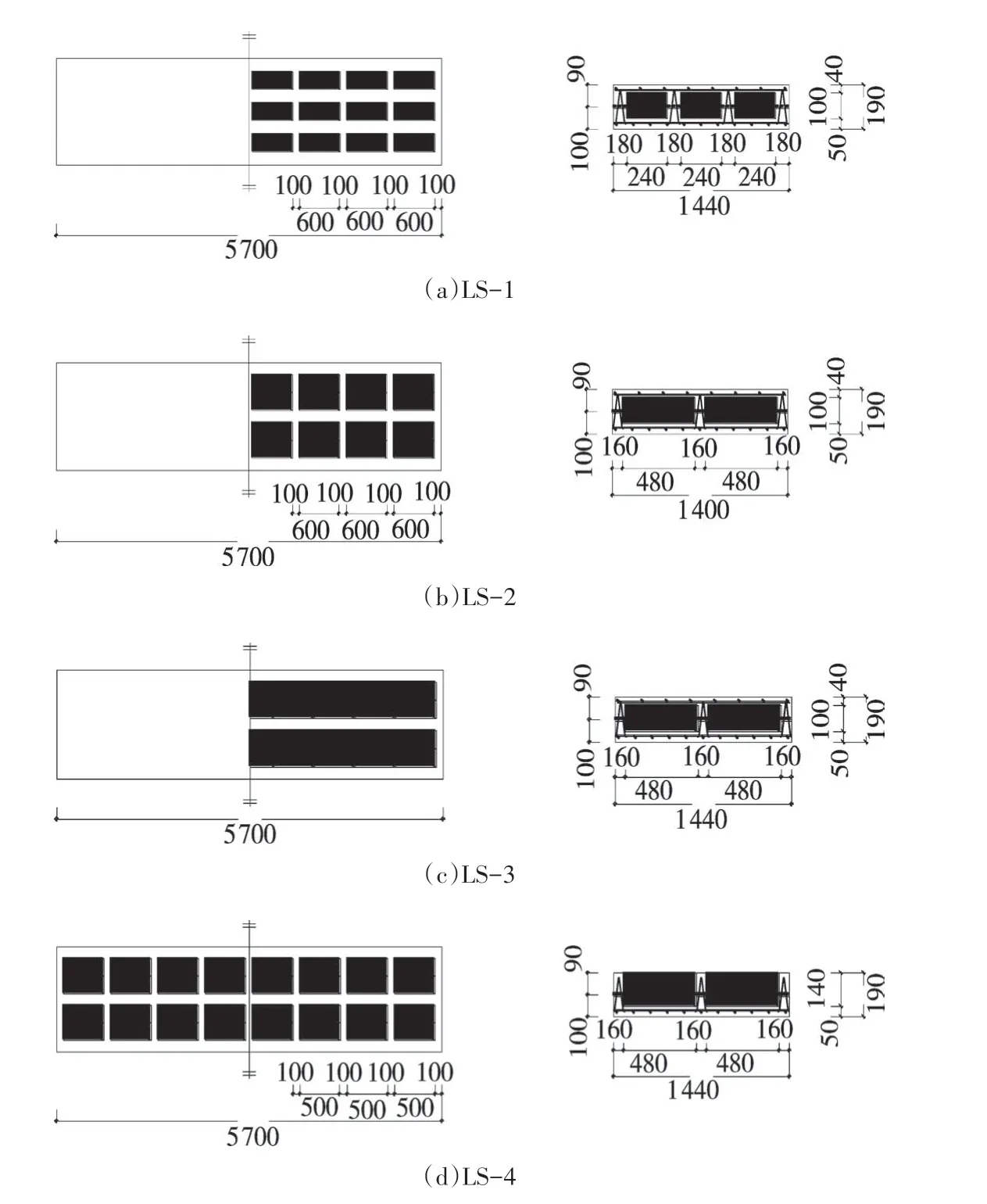
图2 复合叠合板的几何尺寸及构造(单位:mm)Fig.2 Geometric dimensioning and shape of CCSs(unit:mm)
1.2 试件制作
4 块复合叠合板制作过程主要包括预制底板及后浇层制作两道工序:
1)预制底板制作顺序依次为:清理模胎,支放侧模板,涂刷脱模剂,绑扎钢筋网,布置钢筋应变片,浇筑50 mm 厚混凝土,之后将浸泡24 h 后的加气块(用以保证其与混凝土的黏接性)放入设计指定位置[12],再浇筑50 mm 混凝土,待混凝土初凝后将所露的混凝土表面进行人工粗糙面处理[13].
2)后浇层制作工序顺序依次为:以预制底板为底部模板支放侧部模板,涂刷脱模剂,浇筑后浇层混凝土至距板顶20 mm 处,放入后浇层构造钢筋网,继续浇筑至试件顶,形成复合叠合板.
1.3 材料性能
5 块试件为同批次制作.试件浇筑时,同期制作边长为150 mm 的标准立方体及边长为150 mm×150 mm×300 mm 的标准棱柱体试块(每种尺寸均为3块),标准养护28 d后,实测4块复合叠合板的预制底板及试件LS-5 所用混凝土的立方体抗压强度平均值为32.2 MPa,轴心抗压强度平均值为18.9 MPa;4块复合叠合板的后浇层混凝土立方体抗压强度平均值为27.7 MPa,轴心抗压强度平均值为17.6 MPa.实测试件中12钢筋的屈服强度及抗拉强度平均值分别为420 MPa、598 MPa;10钢筋屈服强度及抗拉强度平均值分别为411 MPa、583 MPa.
1.4 加载方案及测点布置
试验采用在板跨度三分点位置施加2 个相等的竖向集中荷载模拟均布荷载的方法,加载点使用30 t 油压千斤顶,加载装置如图3所示.

图3 试件静载加载现场Fig.3 Loading test site of specimens
当试件达到跨中挠度超过跨度的1/50、后浇层顶部混凝土被压碎、底部受拉纵筋被拉断、试件断裂或试件表面出现剥落的条件之一时,认定试件已达到承载能力极限状态并停止加载[14].
试件中钢筋应变片贴于板底纵向受拉钢筋跨中位置;位移计及混凝土应变片布置如图4所示.

图4 试件的混凝土应变及位移计测点布置(单位:mm)Fig.4 Location of strain gauges and LVDTs of specimens(unit:mm)
2 试验结果分析
2.1 承载能力及破坏特征
5块试件最终破坏均是由于挠度、最大裂缝或者受拉主筋应变值超过限值要求而破坏.由图5(试件最终裂缝分布图)及表2(试验实测各试件特征荷载值)可看出:

表2 试件特征荷载Tab.2 Characteristic loads of specimens kN
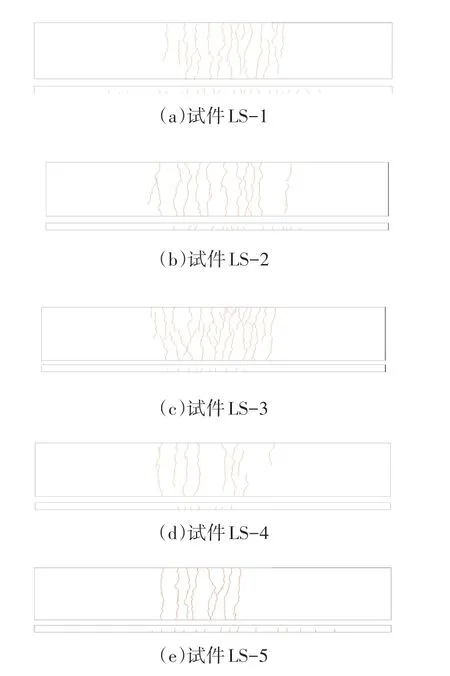
图5 试件裂缝分布Fig.5 Crack distribution of specimens
1)LS-5 的开裂荷载分别比LS-1~LS-4 大64.71%、79.48%、75%、75%,但随着荷载的增加,其屈服荷载却分别比LS-1~LS-4 小38.58%、30.20%、29.71%、22.81%;试件破坏时,LS-5 的极限荷载分别比LS-1~LS-4 小32.17%、28.27%、26.60%、27.30%.本文认为造成这一现象的原因主要是4 块复合叠合板内部配置钢筋桁架所致[15].
2)4块复合叠合板的开裂荷载相差不大,说明本次所设计的4 种构造形式对开裂荷载影响不大.但随着荷载增加,试件承载能力差异逐渐显现,LS-1的屈服荷载及极限荷载最高,说明纵肋间距对后期承载能力影响较大.
2.2 受弯性能
2.2.1 荷载-挠度曲线
由图6 所示荷载(F)-跨中挠度(δ)曲线分析知(图中试验所测挠度值为依据文献[14]中的规定,乘以修正系数ψ(0.98)后的值):
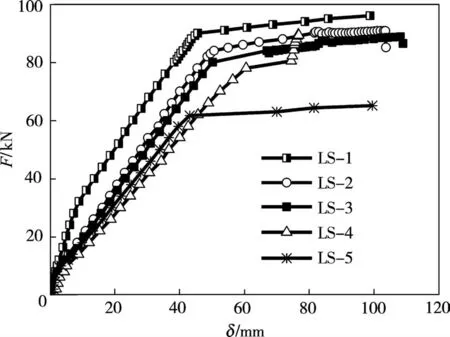
图6 试件荷载-跨中挠度曲线Fig.6 Load-deflection curves at mid-span of specimens
1)5 块试件的曲线均呈明显的三段式分布.加载初期,曲线近似为一条直线,此时试件刚度较大,挠度较小;当底部受拉区混凝土开裂后,由于试件的弯曲刚度的减小,曲线均出现第一个明显的拐点;此后曲线呈现攀爬式的曲线特征,随着受拉钢筋逐渐屈服,曲线出现第二个明显的拐点;此后随加载的继续,除LS-4 外,其他试件的曲线趋势基本呈平行于挠度轴一侧发展,呈现破坏前较好的弯曲变形特征.
2)4 块复合叠合板在同级荷载作用下,LS-1 的挠度最小,说明纵肋间距对提高试件弯曲刚度最为显著;LS-2 与LS-3 的曲线较为接近,尤其是在弹性阶段曲线基本重合,说明是否设置横肋对试件的弯曲刚度影响较小;LS-4 的挠度最大,且在加载后期从曲线看出有滑移现象出现(见2.3节),说明加气块位置对试件刚度有较大的影响.
2.2.2 荷载-钢筋应变曲线
由图7 所示各试件的荷载(F)-跨中纵筋应变(ε)曲线分析知:

图7 试件荷载-钢筋应变曲线Fig.7 Load-rebar strain curves at mid-span of specimens
1)5 块试件曲线均呈三段式发展,同时由于4 块复合叠合板在纵肋中配置了桁架钢筋,有效分担了底部纵向受拉钢筋所受的拉应力,因此在同级荷载作用下,其钢筋应变值均小于LS-5[16].
2)4块复合叠合板在同级荷载作用下,由于试件LS-1 的桁架钢筋数量要比其他3 块试件多1 道,其分担底部钢筋的拉应力作用也较其他3 块要更显著一些,进而其板底纵向受力钢筋的应变在同级荷载下小于其他3块复合叠合板.在钢筋屈服前,LS-2与LS-3 底部纵向受拉钢筋应变较为接近,仅在破坏阶段,试件LS-2 的受拉钢筋应变值略大于LS-3,说明横肋对试件受拉钢筋受力影响较为微弱;LS-4 底部纵向受拉钢筋拉应变在受弯过程中均大于LS-2,但破坏阶段,由于LS-4 出现滑移(见2.3 节),造成板底纵向受拉钢筋未出现屈服平台阶段,而在后期一致保持直线上升,说明加气块位置对试件底部纵向受拉钢筋受力有一定影响.
2.3 整体工作性能
图8 所示为布置于4 块复合叠合板的预制底板与后浇层之间板端位移计所测得的试件板端荷载(F)-滑移(Δ)曲线,可以看出:
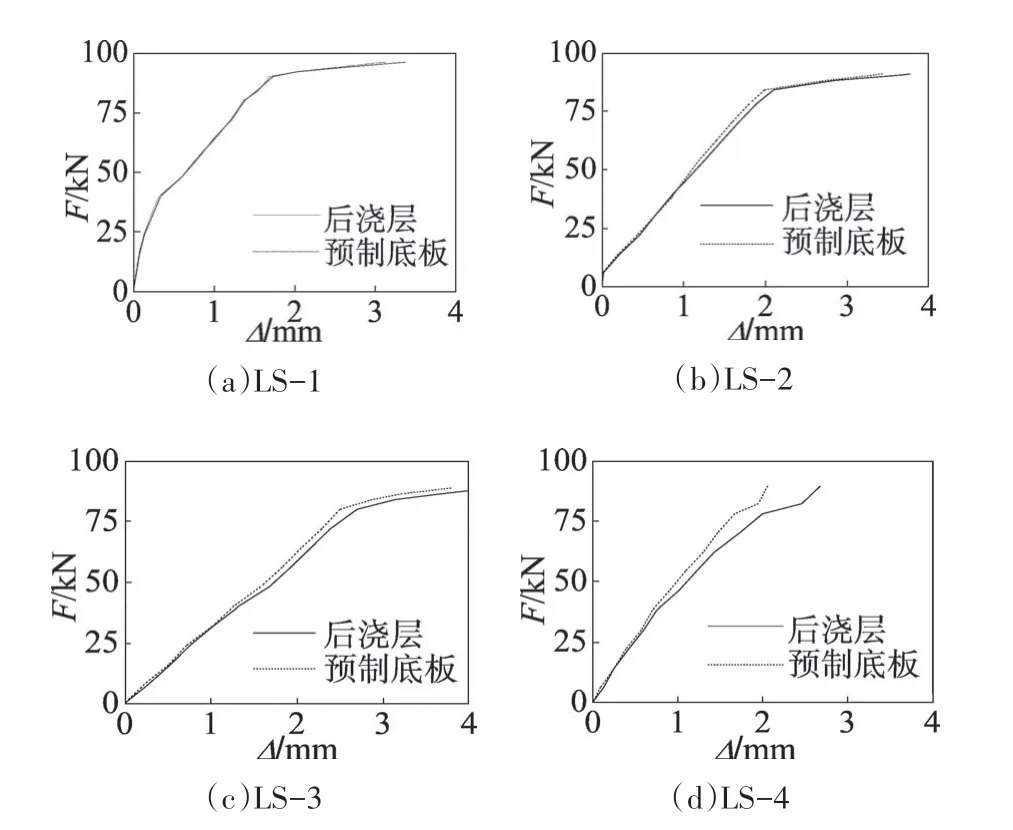
图8 复合叠合板荷载-板端滑移曲线Fig.8 Load-slip curves of CCSs
1)4 块复合叠合板在弹性阶段中预制底板与后浇层均保持良好的协同工作性能,均未出现滑移现象.
2)进入弹塑性阶段,尤其到加载后期的破坏阶段,4 块复合叠合板中,LS-4 出现了明显的预制底板与后浇层间的滑移现象,结合图6 也可看出,在加载后期其荷载-挠度曲线也由于滑移现象而呈现曲线继续上升的趋势,说明该类叠合板中加气块位置对是否出现预制底板与后浇层之间的滑移有较大影响[17-18].
3 弯曲刚度计算
3.1 弯曲刚度影响因素分析
3.1.1 纵肋
举一个例子,现在进行时有两层含义:当下此刻正在发生,以及最近一段时间正在发生。当学生学习现在进行时的意义时,可能对这两层含义有所混淆,不是很理解,这时,教师就可以列举不同组的例子,让学生感受其不同:I am writing a novel now/I am writing a novel recently;She is dancing at this moment/She is dancing these weeks.多样的简单句便可以很好呈现含义的区别,学生理解不再有困难,学习动机也会加强。
从本次试验所得到的图9 中LS-1 与LS-2 在整个加载过程中的弯曲刚度(提取图6 中的切线所绘制)也可看出:在荷载值为(0~40%)Fy时,试件LS-1的弯曲刚度明显大于试件LS-2;随着荷载的增加,两块试件的刚度逐渐接近.本文认为,造成这一现象的原因主要是试件LS-1 的纵肋间距最小,所以其在受弯过程中,剪力滞后效应影响最小,使得正截面受弯较为均匀,而在弹塑性阶段后期,由于内力重分布作用,使得剪力滞后效应有所缓解[19-20].
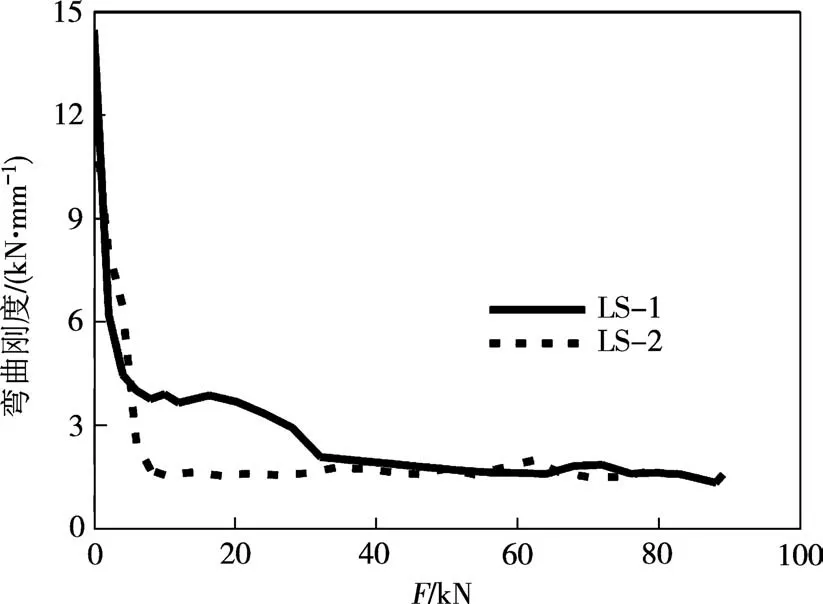
图9 LS-1与LS-2抗弯刚度对比曲线Fig.9 Comparison curve of bending stiffness between LS-1 and LS-2
3.1.2 横肋
由图10 所示LS-2 与LS-3 的弯曲刚度对比图(方法同图9)可看出,在整个加载过程中两者刚度值及变化趋势基本一致,说明横肋对单向受力复合叠合板弯曲刚度影响较小.

图10 LS-2与LS-3抗弯刚度对比曲线Fig.10 Comparison curve of bending stiffness between LS-2 and LS-3
3.1.3 加气块
文献[21]研究表明,内置砖块填充体对双向低肋大跨度板弯曲刚度贡献较小,可仅将其作为恒荷载考虑;《现浇混凝土空心楼盖技术规程》(JGJ/T 268—2012)[22]也规定,“且只有填充体弹性模量为混凝土弹性模量的10%以上时,其才会参与楼板的受力”.
本次试件的填充体均为加气块,其弹性模量仅为混凝土的3.67%,且由图11(LS-2与现浇板弯曲刚度对比图)可看出:在整个加载过程中,加气块仅在弹性阶段(80%Fcr以内)对试件受弯性能有一定影响;随着荷载增加,其影响逐步减弱.因此单向复合叠合板在受弯过程中的受力性能可视同空心板来分析计算.
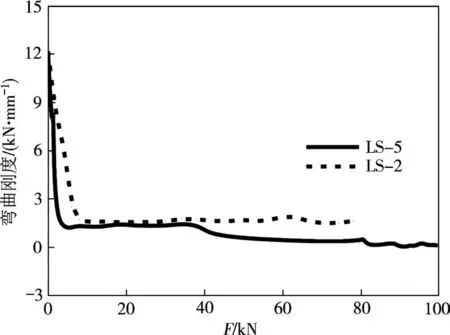
图11 LS-2与LS-5抗弯刚度对比曲线Fig.11 Comparison curve of bending stiffness between LS-2 and LS-5
3.2 计算假定及公式
基于以上分析,本次对4 块复合叠合板短期弯曲刚度计算采用以下假定:
1)所有试件的弯曲过程均满足平截面假定;2)开裂前、后弯曲刚度均采用基于有效惯性矩的计算方法;3)试件开裂前的纵肋简化:采用《混凝土结构设计规程》(GB 50010—2010)[23](以下简称“《混规》”)中对梁类试件有效翼缘宽度的计算方法;4)不考虑填充体及横肋.
3.2.1 开裂前弯曲刚度
选取跨中位置截面作为研究对象,4块复合叠合板在开裂前截面弯曲刚度计算公式为:

式中:B0表示开裂前试件跨中正截面弯曲刚度;E0为混凝土初始弹性模量;I0为开裂前正截面的换算惯性矩(依据图12的计算模型计算).
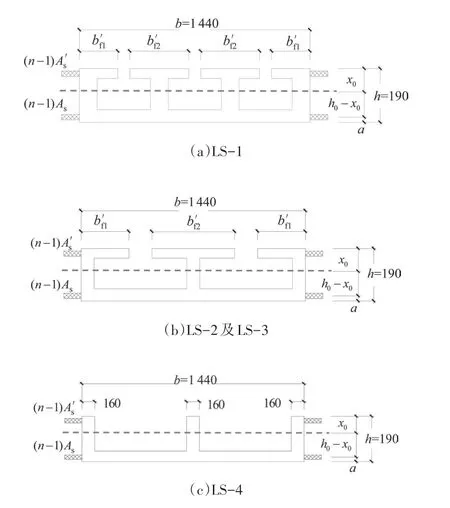
图12 开裂前正截面计算模型Fig.12 Calculation model of section before cracking
图12 中:As与As′分别为底板纵向受拉钢筋面积及顶部受拉钢筋面积(计入钢筋桁架下弦);b′f1、b′f2分别为依据《混规》中倒L形、T形截面换算的有效翼缘计算宽度;x0为依据上述模型换算后的中性轴上部受压区截面高度;h0为试件有效截面高度.
3.2.2 开裂后弯曲刚度
选取跨中正截面作为研究对象,在混凝土开裂后4块复合叠合板弯曲刚度计算公式为:

式中:Beff为试件开裂后的弯曲刚度;Ieff表示有效惯性矩,采用美国《钢筋混凝土房屋设计规范》(ACI 318M—05)中的计算方法[24](在I0与Icr之间进行插值计算得出):
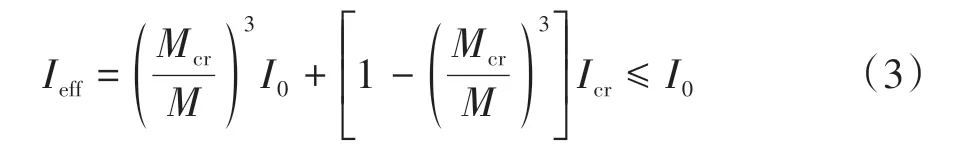
式中:Icr为不考虑底部受拉区混凝土的截面惯性矩,采用图13 的计算模型计算;Mcr为截面开裂荷载,采用公式Mcr=γftkW0计算,具体取值及含义见《混规》;M为试件所受弯矩.

图13 弹塑性阶段正截面计算模型Fig.13 Calculation model of section in elastoplastic
3.3 计算验证
公式(4)为三分点集中荷载作用下试件跨中截面挠度计算公式.

式中:F为试件所受荷载值;B为短期弯曲刚度,其值依据3.2 节中开裂前、后的各试件弯曲刚度公式计算;l0为试件计算跨度.
取0~Fy之间的实测荷载值计算所得4 块叠合板试件的短期挠度与试验值的荷载挠度对比曲线(见图14)可以看出:在荷载值为0~Fcr时,LS-1的计算值与试验值之间平均误差为8.66%、LS-2 为3.31%、LS-3 为11.30%、LS-4 为12.30%;在荷载值为Fcr~Fy时,试件LS-1 的计算值与试验值之间相对平均误差为12.04%、LS-2 为12.48%、LS-3 为12.82%、LS-4 为19.21%.

图14 试验与计算荷载-跨中挠度对比曲线Fig.14 Comparison curve between test and calculation load-deflection curves at mid-span
由此可见,按上述方法计算的试件LS-1、LS-2及LS-3 计算值与试验值误差均在10%左右,具有一定参考价值.而试件LS-4 在开裂后计算值与试验值误差较大,本文认为,这是由于其后期出现部分滑移现象所导致的.
4 结论
1)复合叠合板与普通混凝土现浇板的受弯破坏过程类似,破坏前均有较明显的特征,且裂缝分布也基本相似,呈典型的单向板破坏模式,现浇板的开裂荷载高于复合叠合板,但屈服荷载及极限承载能力均低于复合叠合板.
2)不同的构造形式对复合叠合板的受弯性能有一定影响,依据分析,其影响因素从大到小依次为:纵肋>填充块是否外露>横肋.其中:a)纵肋间距的增大会造成顶部薄板剪力滞后效应,进而影响试件在加载前期的刚度及承载能力的发挥;b)加气块及横肋对试件弯曲刚度的贡献基本可忽略不计;3)加气块顶置会造成该类板件出现滑移.
3)本文建议该类复合叠合板的短期弯曲刚度在弹性阶段可采用《混范》中对受弯构件受压区的有效翼缘宽度计算方法计算正截面的开裂前弯曲刚度;在弹塑性阶段可采用不考虑加气块及横肋的全截面计算弯曲刚度方法.
