移动荷载下波形钢腹板曲线组合梁桥动力特性研究
2023-01-31董海雷张彦玲
董海雷, 王 灿, 张彦玲
(1.石家庄铁道大学土木工程学院,河北 石家庄 050043;2.中铁大桥科学研究院有限公司,湖北 武汉 430034;3.桥梁结构健康与安全国家重点实验室,湖北 武汉 430034)
波形钢腹板与混凝土组合桥梁结构的投入使用,不但保证了正常的受力性能,更兼具经济适用和便于施工等特点,因此其慢慢被应用于我国的桥梁工程建设之中。然而,关于波形钢腹板组合梁桥的车桥冲击振动问题一直以来未有统一的解决方法。而且目前大多研究集中在波形钢腹板组合桥梁的静力性能研究方面[1-3],张永健[4]、戴青年[5]、郑尚敏等[6]利用理论推导加有限元仿真以及室内试验三者结合的方法对波形钢腹板PC组合箱梁竖向自振特性进行了研究。在自振特性研究的基础上,肖英楠[7]、王妍[8]、戚伟利[9]、张政韬[10]对移动车辆荷载作用下的波形钢腹板PC组合箱梁动力特性进行了研究,但研究对象均为直线桥。
本文采用理论分析方法,综合考虑曲梁弯扭耦合、腹板剪切变形及箱梁的约束扭转,利用能量变分法和哈密顿原理对移动荷载作用下桥梁的竖向动力特性解析解进行推导,同时探究箱梁腹板剪切变形和箱梁约束扭转对曲梁自振及强迫振动的影响。
1 移动荷载-波形钢腹板组合梁桥的理论解推导
在推导过程中采用的基本假定包括:
(1)曲梁的运动满足小变形理论并在弹性范围内线性理论适用。
(2)满足简单梁理论,曲梁质量分布均匀,具有恒定的双对称横截面,符合平截面假定,不考虑截面的剪力滞效应,综合考虑腹板剪切变形、约束翘曲,曲梁由恒定的横截面构成,翘曲阻力可忽略不计。
(3)假定与桥梁相比,车辆的惯性效应很小,因此仅考虑车辆的重力效应,忽略车辆的惯性效应,将其简化为一个集中的移动荷载力;车辆以恒定速度在曲梁上移动,无滑移,并与桥梁表面持续接触,车辆在上桥之前,曲梁处于静止状态。
(4)由于移动荷载的作用时间较短,因此阻尼因素对桥梁的影响很小,不考虑曲梁的阻尼效应,同时忽略桥面的粗糙度。
1.1 计算模型
在推导过程中采用的曲梁截面形式及梁上移动荷载运动轨迹如图1和图2所示。简支梁为截面恒定的曲线梁,梁高为h,梁宽为b,顶底板厚度为δ;下标u,b分别表示混凝土顶板和底板的相应特性(以下同),zu为截面形心到顶板形心的距离,zb为截面形心到底板形心的距离;θ为曲梁弧线圆心角;R和l分别为曲梁的曲线半径和曲线跨度。
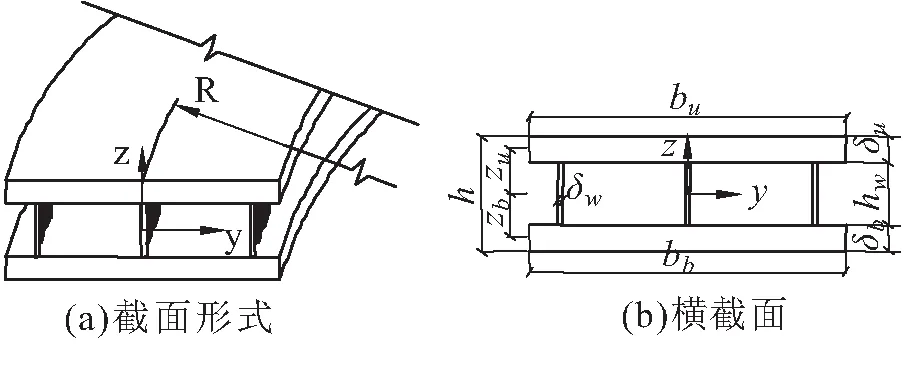
图1 单箱双室波形钢腹板组合梁截面形式
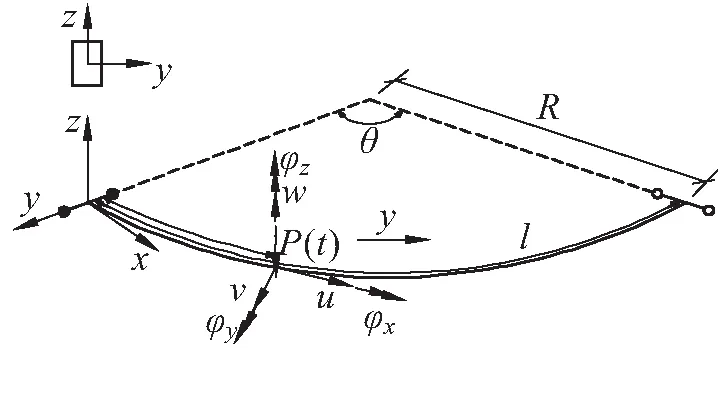
图2 移动荷载下曲梁示意图
选择右手坐标系,其中y轴和z轴与横截面的主轴重合,x轴与梁的质心轴相切。设u、v和w分别为曲梁每个横截面的质心沿x、y、z轴的位移,φx、φy和φz分别为围绕三个轴的扭转角。荷载P(t)以匀速v向右移动,当t=0时,荷载位于最左端支撑处;在时间为t时,荷载运动距离为vt。
由文献[11]可得一般简支曲梁的微分方程为:
竖向位移,
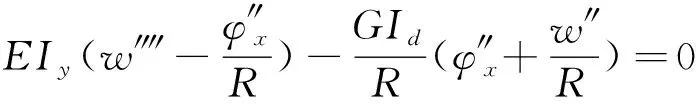
(1)
扭转位移,
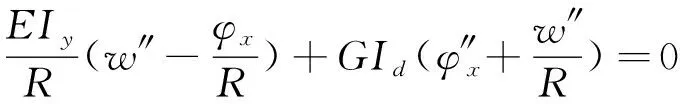
(2)
式中:w′为对曲梁的纵向微分;φ′x为对绕x轴扭转角的微分;E和G分别为曲梁的弹性模量和剪切模量;Iy为关于y轴的惯性矩;Id为曲梁的扭转惯性矩。
1.2 弯曲应变能
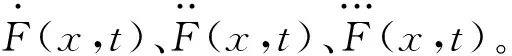

(3)


(4)
则得到弯曲总动应变能为:
Vw(t)=Vwu(t)+Vwb(t)
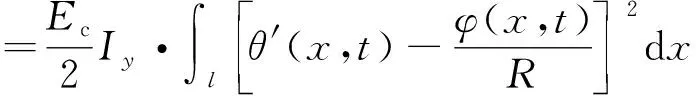
(5)
1.3 约束扭转翘曲应变能
由乌曼斯基的闭口截面薄壁杆件约束扭转理论,建立多室闭口截面杆件约束扭转计算公式,其中自由扭转剪力流q的方程为:
式中:i=1,2,…,n,n为室数;k为与相邻箱室共同室壁;φ′(x,t)为截面扭率;Ωi为箱室中心线所围面积的2倍;由于波形钢腹板组合箱梁顶、底板与腹板的材料及厚度不相同,故采用换算截面,将钢材转换成混凝土,G全部取混凝土的切变模量Gc。由于波形钢腹板的褶皱效应,其切变模量Gs采用等效切变模量Ge表示。假定换算后的钢腹板高度不发生变化,则其等效厚度δ′w为:
式中:δw为波形钢腹板板厚;a、c、ψ具体参数见图3所示。
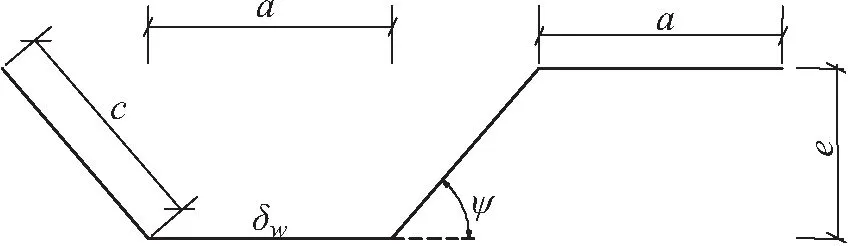
图3 波形钢腹板波段结构
计算曲线闭口箱梁在扭转作用下的截面纵向翘曲位移uω(x,s,t),取截面形心轴与箱壁交点为积分零点,可得约束扭转翘曲正应力σx(x,s,t),从而得到刚性扭转翘曲应变能为:
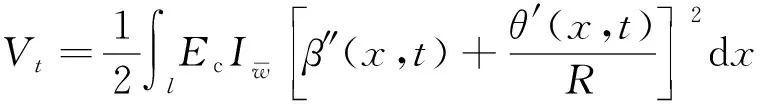
(6)
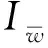
1.4 钢腹板剪切动应变能
截面波形钢腹板考虑剪切变形时,则箱梁腹板的剪应变可表示为η(x,t)=w′(x,t)-θ(x,t),则相应的动应变能为:
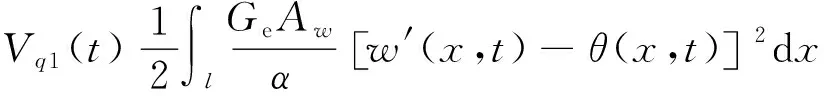
(7)
式中:Aw为波形钢腹板剪切面积,Aw=nδwhw,n为钢腹板列数;α为平截面假定修正系数,取α=1.2。
1.5 约束扭转剪切动应变能
曲线箱梁截面上的总扭矩可表示为自由扭转扭矩Td(x,t)和约束扭转扭矩Tω(x,t)之和,有:
Gc(Iρ-Id)[β′(x,t)-φ′(x,t)]
(8)
则约束扭转剪切应变能为:

(9)
式中:Iρ为极惯性矩。
1.6 动能
波形钢腹板组合梁以竖弯为主模态振型的动能:
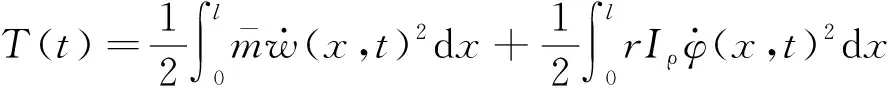
(10)

1.7 非保守力作功
由于只有外力P(t)作功,则非保守力作的虚功等于:

(11)
式中:Wnc(t)为非保守力;ϑ为Dirac函数。
1.8 移动荷载下波形钢腹板曲线组合梁的受迫振
动方程
根据Hamilton原理,一个平衡的体系在任何时间区间t1到t2内,动能和位能的变分加上所考虑的非保守力所做的功的变分必须等于零。即
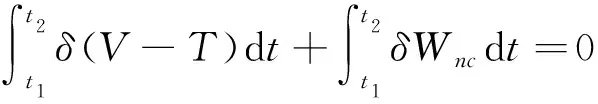
(12)
将式(5)、式(6)、式(7)、式(9)、式(10)和式(11)代入式(12),根据变分原理,得到波形钢腹板曲线组合箱梁在强迫振动下的运动方程组为:
(13)
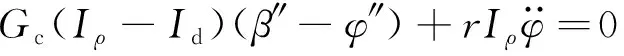
(14)
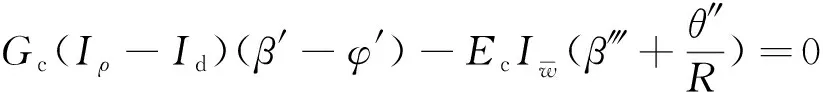
(15)
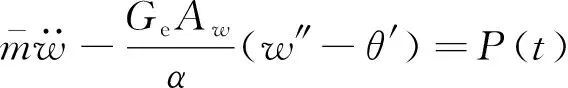
(16)
边界条件为:
1.9 振动方程的求解
本节利用伽辽金法进行求解,针对简支曲线箱梁的挠度w、扭转角φ、扭转翘曲广义位移、弯曲转角θ,假设其形函数分别为:
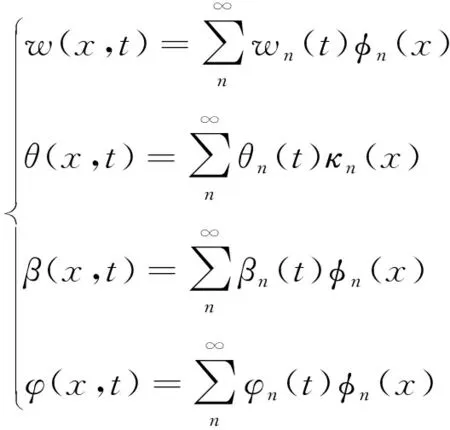
(17)
式中:wn(t)、θn(t)、βn(t)、φn(t)为广义振型坐标,是时间t的函数;φn(x)与κn(x)为主振型函数,波形钢腹板简支曲线组合梁竖弯振型中挠度w(x,t)、扭转角φ(x,t)均在支座处为0,在跨中处达到峰值,形函数采用正弦函数;扭转翘曲广义位移函数β(x,t)与扭转角φ(x,t)具有相似特性,也设为正弦函数;截面转角θ(x,t)在两端支座处达到最大值,在跨中取值为0,形函数可采用余弦函数表示。有:
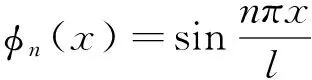
(18)

(19)
将式(18)和式(19)代入式(17),将式(17)代入式(13)~ 式(16),得到
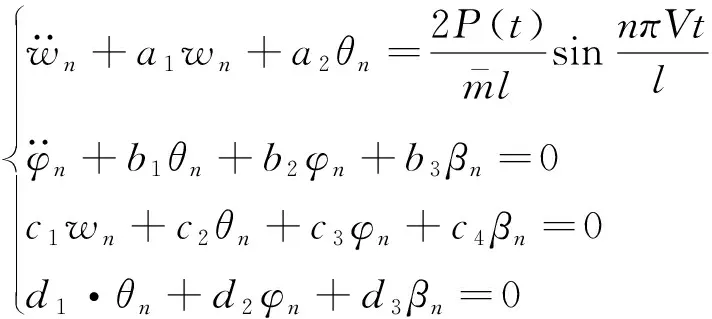
(20)
式中:a1、a2、b1、b2、b3、c1、c2、c3、c4、d1、d2、d3表达式如下,
d2=-Gc(Iρ-Id)

将式(20)方程组中的通解分成两部分求解,即齐次解wnh、θnh、φnh、βnh和特解Pwn、Pθn、Pφn、Pβn,得齐次解求解矩阵为:
得到曲梁自振圆频率为:

(21)
曲梁自振频率为:

(22)
k1=d1-c2·d3,k2=b1·(c4·d2-c3·d3)+
c2·(a1·d3-b3·d2+b2·d3)-a2·c1·d3+
d1(b3·c3-a1-b2),k3=a1·b1·(c3·d3-
c4·d2)-a1·b3·c3·d1+(b2·d3-b3·d2)·
(a2·c1-a1·c2)
特解求解矩阵为:


(23)
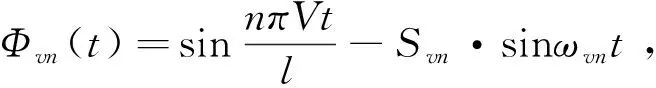

(24)
本公式利用数学软件MATLAB进行求解。
2 算例
本文采用文献[5]中的CSB2试验梁(计算跨径4.4 m,曲线半径8.8 m,跨径比0.5)自振及相关有限元结果,对理论推导结果进行验证。曲梁CSB2截面尺寸如图4所示。
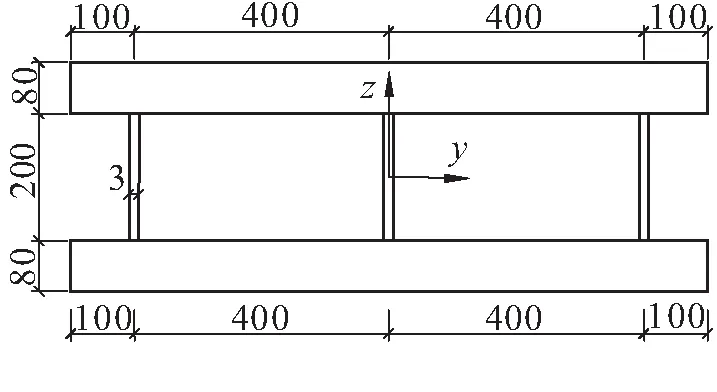
图4 单箱双室波形钢腹板组合梁截面尺寸(单位:mm)
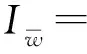
在有限元软件ANSYS中建立相应曲梁模型如图5所示。

图5 单箱双室波形钢腹板组合梁模型
其中自振基频对比如表1所示。

表1 波形钢腹板曲梁竖向自振基频对比
假定移动荷载为P(t)常量力,取P=1 000 N,移动速度取20 m/s。跨中竖向动挠度对比如图6所示。
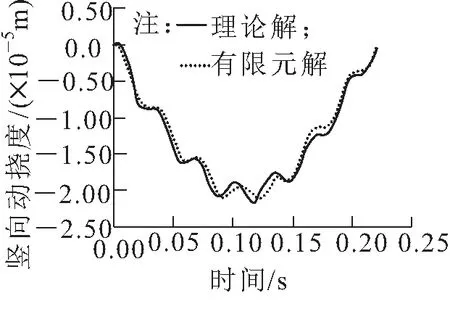
图6 曲梁跨中竖向动挠度有限元解、理论解对比
由表1及图6可以看出,理论计算自振基频结果与试验及有限元结果对比相对误差均在5%以内,理论计算跨中挠度曲线与有限元计算曲线变化趋势基本相同,验证了理论推导的正确性。
3 箱梁约束扭转及腹板剪切变形对波形钢腹板曲梁动力特性的影响
在文献[5]提供的单箱双室波形钢腹板曲线简支箱梁CSB2截面及本文所做理论推导的基础上,考虑如下四种情况:
工况一,不考虑剪切变形和约束扭转,将曲梁假设成简单的欧拉梁,有扭转翘曲应变能为零且η(x,t)=w′(x,t)-θ(x,t)=0,其它能量参数保持不变,求得的自振基频及跨中竖向动挠度分别记为f1和w1。
工况二,考虑约束扭转,不考虑腹板剪切变形。有η(x,t)=w′(x,t)-θ(x,t)=0,其它能量参数保持不变,自振基频及跨中竖向动挠度分别记为f2和w2。
工况三,考虑腹板剪切变形,忽略箱梁约束扭转,只考虑自由扭转。此时扭转翘曲应变能为零,约束扭转剪切动应变能只由自由扭转贡献,其它能量参数保持不变,由此得到的自振基频及跨中竖向动挠度分别记为f3和w3。
工况四,同时考虑腹板剪切变形和箱梁约束扭转,由此得到的自振基频及跨中竖向动挠度分别记为f4和w4。自振基频对比结果见表2所示。

表2 四种工况下曲梁竖向自振基频对比
假定移动荷载为P(t)常量力,取P=1 000 N,移动速度取20 m/s。将理论计算结果与有限元结果进行对比,结果见图7所示。

图7 四种情况下的曲梁跨中竖向动挠度时程
由表2及图7可以看出,工况二相对工况一欧拉梁误差较小,工况三及工况四误差较大,说明箱梁约束扭转对波形钢腹板曲线组合梁的车辆冲击振动响应影响较小,腹板的剪切变形影响较大。
4 结论
(1)本文采用能量变分法推导了波形钢腹板简支曲线组合梁在移动荷载下的振动微分方程,采用伽辽金法求解得到了其在移动荷载作用下的理论解,并通过与试验值及有限元值对比验证了理论解的正确性。
(2)在理论推导的基础上,探究了箱梁腹板剪切变形和箱梁约束扭转对波形钢腹板曲梁动力特性的影响,结果表明:箱梁约束扭转对波形钢腹板曲线组合梁的车辆冲击振动响应影响较小,腹板的剪切变形影响较大,计算中不应忽略。
