新型单层递归神经网络解决非光滑伪凸优化问题的研究
2023-01-31黄晓燕
喻 昕,黄晓燕
(广西大学 计算机与电子信息学院,南宁 530004) (广西多媒体通信与网络技术重点实验室,南宁530004)
1 引 言
众所周知,优化问题广泛应用于科学和工程等领域,如:信号处理、模式识别、机器学习及博弈论等,具有重要的研究意义.为了解决优化问题,众多学者提出了各种算法.但大多数算法无法实时求解,并且普通的数值计算方法难以在短时间获取复杂优化问题的最优解.自1986年Tank和Hopfield[1]率先提出使用神经网络解决线性规划问题以来,许多研究学者不断提出各种神经网络模型以求解非线性优化问题[2-6].如文献[7]中,Qin等人基于Lyapunov函数和拓扑度理论提出了一种有效的神经网络模型,该神经网络模型需要较强的假设条件才可以满足收敛;Bian和Xue[8]基于次梯度和罚因子的理论提出了一种递归神经网络模型,但该模型需预先计算惩罚因子;Qin等人[9]提出了双层神经网络以解决非光滑凸优化问题,而双层模型结构增加了模型硬件实现的复杂度.文献[10],文献[11]及文献[12]分别提出了一种无需计算罚因子的神经网络,且均能解决复杂的非线性优化问题,Qin等人[13]在神经网络中引入了正则化思想,丰富了理论基础.
上述解决的目标函数均为凸或非凸函数,由于伪凸函数相比非凸函数具有更特殊的性质,上述神经网络模型无法直接应用,这促进了学者们对此问题的深入研究.Liu等人[14]构造了一种解决等式约束和方体约束的伪凸优化问题,其不足在于需要计算精确的罚因子;在文献[15]中,Li等人基于正则化的方法,构造了解决伪凸优化问题的神经网络模型,但其初始点的选取需在可行域内且可行域必须有界;Gou等人[16]提出的模型只能解决含有等式约束的伪凸优化问题,其模型的应用范围大大缩小;文献[17]中Qin等人提出了使用微分包含的神经网络,简化了模型,但要求目标函数必须有下界;Li等人[18]在网络模型中引入投影方法,但在某些情况下很难计算投影算子.为了更好解决伪凸优化问题,Liu和Qin[19]在前人基础上引入时变函数提出了一种新的神经动力学模型,Xu等人[20]也提出了新的递归神经网络模型,而该模型构造复杂,不易实现;Yang等人[21]使用逐次凸逼近和逐次伪凸逼近方法来求解伪凸优化问题,该方法存在无法找到精确最优解问题;文献[22]结合伪凸函数的偶合导数及正则化思想构建了数学模型,并验证了其结果在该问题上具有充分最优性.此外,部分学者也将神经网络运用到实际中.如文献[23]中将神经网络应用在人脸表情识别上,文献[24]结合金融数据的特点用神经网络模型对金融市场进行波动程度进行预测.冯诗影等人[25]将循环神经网络运用在语音识别中,并优化了识别效率.
为了解决上述神经网络模型的不足,在现有理论及前人工作的基础上,本文提出了一种基于时变函数的递归神经网络模型来解决含有等式和不等式约束条件的非光滑伪凸优化问题.与已有的模型相比,其优势如下:1)结构比文献[9]简单,仅为单层;2)与文献[16]相比,本文同时能解决等式和不等式限制的伪凸优化问题,应用性更广泛;3)与文献[8]相比,本文无需计算罚因子;4)与文献[8,15]相比,本文的初始点可任意选取.
本文结构及内容如下:第1节,介绍神经网络在优化问题的发展以及国内外研究现状;第2节,介绍研究内容及预备知识;第3节,构造递归神经网络模型;第4节,分析及论证该网络模型;第5节,通过数值实验验证模型的有效性.
2 研究内容及预备知识
2.1 研究内容
本文研究的非光滑伪凸优化问题如下:
minH(x)
s.tq(x)≤0
Ax=b
(1)
其中,x=(x1,x2,…,xn)T∈Rn,A∈Rm×n是行满秩矩阵,b=(b1,b2,…,bm)T∈Rm,目标函数H:Rn→R是正则伪凸的但未必光滑,q=(q1,q2,…,qp)T:Rn→Rp是凸函数但未必光滑.令Q1={x:q(x)≤0},Q2={x:Ax=b},可行域为Q=Q1∩Q2={x∈Rn:q(x)≤0,Ax=b},Q*表示优化问题(1)的最优解集.文中所出现的int(Ω)代表集合Ω的内部集,bd(Ω)代表集合Ω的边界.本文假设优化问题(1)至少存在一个解.B(a,R)表示以a为圆心,R为半径的球体.
2.2 预备知识
下面将介绍一些本文所涉及的相关基础理论,包括集值映射函数、伪凸函数等.
定义1.若对F⊆Rn中的任意x,都存在一个对应的非空集合G(x),则称G:F→Rn是一个由F到Rn的集值映射.若对G(x0)的任意开邻域L,都存在x0的对应邻域U使得G(U)⊆L,则称集值映射G:F→Rn在点x0∈F处为上半连续的.
定义2.设x∈Rn,若f在点x处是lipschitz连续的,则f在点x关于方向v∈Rn的广义方向导数为:
另外,∂f(x)={ξ∈Rn:f0(x,v)≥ξTv,∀v∈Rn}表示f在点x处的Clarke广义梯度.若f在点x处是局部Lipschitz连续的,记Lipschitz常数为C,则∂f(x)为Rn中的非空紧凸子集,且对∀ξ∈∂f(x),都有‖ξ‖≤C.
定义3.令K⊆Rn为一个非空凸集,对任意的x,y∈K,若∃γ∈∂f(x):γT(y-x)≥0⟹f(y)≥f(x)则f:K→R在集合K上是伪凸函数.
定义4.设K⊂Rn为非空闭凸集,点x∈K的法锥为:
NK(x)={v∈Rn:vT(x-y)≥0,∀y∈K}
引理1.若函数f:Rn→R为凸函数,则对于任意选取的x,y∈R,有f(y)-f(x)≥<ξ,y-x>,∀ξ∈∂f(x).
引理2.若函数P:Rn→R是正则函数,x(t):R→Rn是绝对连续的,则对a.e.t∈[0,+∞)有:
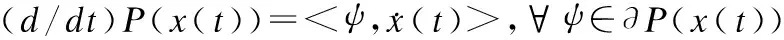
引理3.设K1,K2⊂Rn为非空闭凸集且满足0∈int(K1-K2),则任意的x∈K1∩K2有:
NK1∩K2=NK1(x)+NK2(x)
引理4.设K⊆Rn为非空集合,若函数f在x∈K处Lipschitz连续且达到局部最小,则:
0∈∂f(x)+NK(x)
3 构建神经网络模型
为了更好解决非光滑伪凸优化问题(1),本文提出新的单层递归神经网络模型,其模型需要满足以下的假设条件.
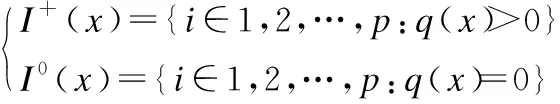
定义等式约束部分的罚函数为:M(x)=‖AT(AAT)-1(Ax-b)‖,M(x)表示x∈Rn到Q2的距离,且Q2={x:M(x)≤0}={x:Ax-b=0}.本文提出如下递归神经网络模型以解决非光滑伪凸优化问题(1):
(2)
其中ε(t)=ε0(1+t)-1/3,ε0≥1.ε(t)是类似Tikhonov的正则化方法,起到惩罚因子的作用,无需计算精确的惩罚因子.I表示单位矩阵,P=AT(AAT)-1A,A是行满秩矩阵,θ:[0,+∞)→[0,1]定义为:
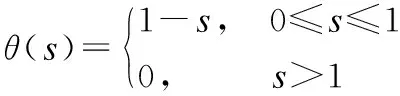
(3)
θ(B(x(t)))进一步控制其解轨迹的有界性.η(t)定义为:
(4)
其中tQ2=‖AT(AAT)-1(Ax0-b)‖,表示到达等式可行域Q2的时间.x0表示初始点的值.本文所提出的神经网络模型(2)可以用电路实现,其实现过程如图1所示.
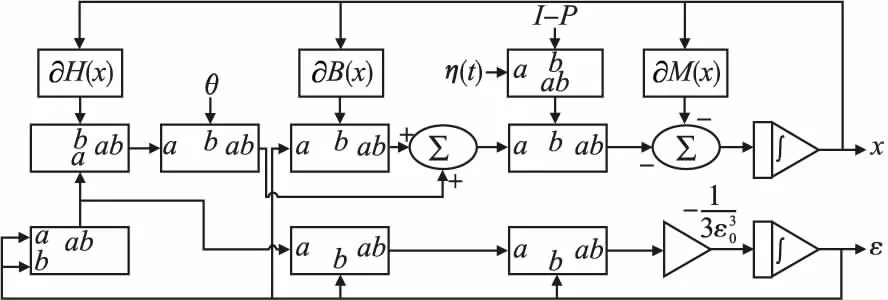
图1 神经网络模型(2)的电路实现图Fig.1 Circuit realization diagram of neural network model(2)
4 主要定理分析及证明
4.1 神经网络局部解的存在性
定理1.若假设(A)成立,则对于任意初始点x0∈Rn,神经网络(2)在时间段t∈[0,T)至少存在一个局部解x(t),其中T∈(tQ2,+∞).
证明:下面可以分两种情况讨论.
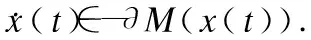
(5)
即在时间段[0,t′)中,x(t)是有界的.再由解的扩展性的理论可知神经网络的局部解在[0,tQ2]时间内是存在的.
当t>tQ2时,神经网络模型为:
经分析得知上式公式右侧部分为一个具有非空紧凸集性质的集值映射函数.与t∈[0,tQ2]时的证明类似,可得对任意初始点x0∈Rn,神经网络(2)在t>tQ2上至少存在一个局部解x(t).
情况(b):x0∈Q2.与证明情况(a)类似,可证得神经网络(2)在时间段t∈[0,T)至少存在一个局部解x(t),其中T∈(tQ2,+∞).
4.2 有限时间状态解收敛到等式可行域
引理5.若假设(A)成立,则有以下结论成立:
证明:当x∉Q2时,M(x)为严格可微函数且:
可得:
当x∈Q2时,∂M(x)={PTζ:‖ζ‖≤1},因此‖∂M(x)‖=‖PTζ‖≤‖P‖‖ζ‖≤1.
定理2.若假设(A)成立,则对任意初始点x0∈Rn,神经网络(2)的状态解x(t)都会在有限时间内进入等式可行域Q2中,并永驻其中.
证明:取L(x)=‖AT(AAT)-1(Ax-b)‖,显然L(x)为正则函数.存在可测函数ξ(t)∈∂H(x(t)),γ(t)∈∂B(x(t)),及ω(t)∈∂M(x(t)),使得对a.e.t∈[0,+∞]有:
从P的定义可知:A(I-P)=0,(I-P)2=I-P,结合引理2可得:
=<ω(t),-η(t)(I-P){ε(t)2θ(B(x(t)))ξ(t)+
ε(t)r(t)}-ω(t)>=-‖ω(t)‖2
(6)
当x(t)∉Q2时,‖ω(t)‖2=1,则
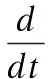
(7)
当x(t)∈Q2时,‖ω(t)‖2≤1,则
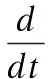
(8)
对式(7)两端从0到T进行积分得‖AT(AAT)-1(Ax(T)-b)‖-‖AT(AAT)-1(Ax0-b)‖=-T,这意味着对于任意的初始点x∈Rn,其神经网络状态解x(t)会在时刻T′=‖AT(AAT)-1(Ax0-b)‖进入到Q2中.
下面使用反证法证明当神经网络状态解x(t)一旦进入等式限制域后,便不再离开.若不然,神经网络(2)的状态解x(t)将在t1时刻离开Q2,且存在t∈(t1,t2), 0≤t1≤t2满足x(t)∉Q2.结合‖AT(AAT)-1(Ax(t1)-b)‖=0及式(7)可得:
‖AT(AAT)-1(Ax(t2)-b)‖=‖AT(AAT)-1(Ax(t1)-b)‖-(t2-t1)=-(t2-t1)<0
(9)
与‖AT(AAT)-1(Ax(t1)-b)‖≥0矛盾,即对任意的x∈Rn,神经网络(2)的解轨迹x(t)都会在‖AT(AAT)-1(Ax0-b)‖时刻进入等式可行域中且不再离开.
4.3 解轨迹的有界性及全局解的存在性
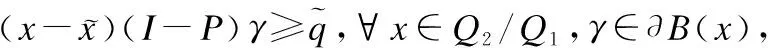
引理7.若假设(A)成立,则不等式的罚函数B(x)是强制的,即:当x∈Q2,‖x‖→+∞时,B(x)→+∞.
证明:可以分为以下两种情形进行讨论:
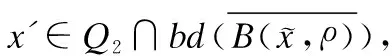
(10)
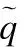
(11)
结合式(10)和式(11)可得:
(12)
结合前文对B(x)的定义,可知:
(13)
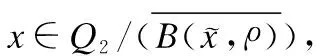
(14)
从式(13)以及式(14)可知当x∈Q2,‖x‖→+∞时,B(x)→+∞成立.
定理3.若假设(A)成立,对任意初始点x0∈Rn,神经网络(2)的解轨迹x(t)都是有界的.
证明:由定理2可知神经网络(2)的解轨迹x(t)会在有限时间内进入等式可行域Q2且驻留其中,即:
x(t)∈Q2={x:Ax=b},∀t≥tQ2
因η(t)=1,∀t≥tQ2.存在可测函数ξ(t)∈∂H(x(t)),γ(t)∈∂B(x(t)),及ω(t)∈∂M(x(t)),使得对a.e.t∈[tQ2,+∞]有:
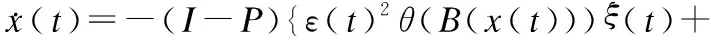
(15)
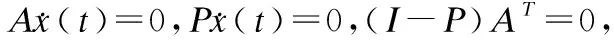
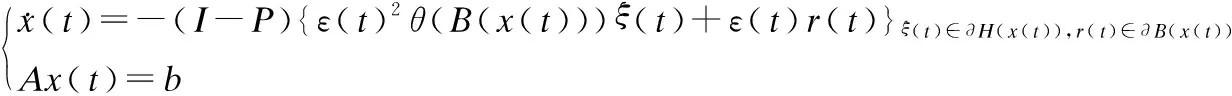
(16)
一方面从引理7可得存在R′>0满足:
(17)
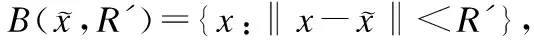
(18)
θ(B(x(t)))=0,∀t∈(t′,t′+τ]
(19)
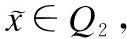
(20)
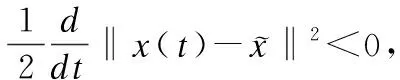
综上,可证得神经网络(2)的解轨迹x(t)是有界的.
定理4.若假设(A)成立,则对于任意初始点x0∈Rn,神经网络(2)至少存在一个全局解x(t),∀t∈[0,+∞].
证明:设x(t)为初始点x0∈Rn的神经网络(2)的解轨迹,由定理3可知x(t)有界,结合定理1以及解的可扩展性理论可以得出神经网络(2)至少存在一个全局解x(t),∀t∈[0,+∞].
4.4 有限时间收敛到可行域Q
定理5.若假设(A)成立,对任意初始点x0∈Rn,神经网络(2)的解x(t)会在有限时间内进入可行域Q中且驻留其中.
证明:由定理2可知,对任意初始点x0∈Rn,神经网络(2)的状态解x(t)都会在有限时间内进入等式可行域Q2且驻留其中.当t>TQ2,η(t)=1,神经网络(2)等价为式(16),因此只需证明对任意初始点x0∈Q2,神经网络(16)的解轨迹在有限时间内进入到可行域Q1且驻留其中即可.回顾定理3分析过程中的式(18)和式(19)可以将x∈Q2/Q1时的θ(B(x))分为以下两种情形:
当x∈{x:0
由定理3可知x(t)有界,即存在R′>0使得:
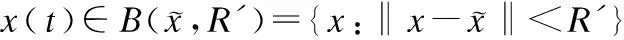
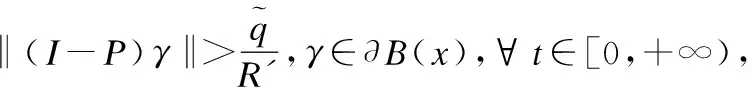
下面使用反证法证明定理5.若神经网络(2)不能在有限时间之内进入不等式可行域Q1并驻留其中,则必有以下两种情形之一发生:
情形1.存在T>tQ2,使得对任意的t>T有x(t)∈Q2/Q1,0≤θ(B(x))<1.结合引理2、引理6及(I-P)2=I-P,‖I-P‖≤1可知存在可测函数ξ(t)∈∂H(x(t)),γ(t)∈∂B(x(t))使得对于几乎所有时间t∈[T,+∞):
ε(t)r(t)}>≤ε(t)2θ(B(x(t)))ξ(t)‖γ(t)(I-P)‖-ε(t)‖γ(t)(I-P)‖2
(21)
若0≤θ(B(x))<1时,式(21)即为:
(22)
对式(22)两端进行从T到t积分得:
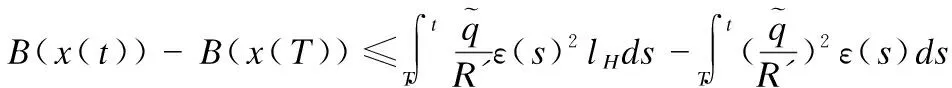
(23)
与上述证明类似得知与B(x(t))的非负性矛盾.
综上讨论,情形1不成立.
情形2.存在互不相交的开区间列(αn,βn)满足:
2)x(t)∉Q1,∀t∈(αn,βn);
3)B(x(αn,))=0.
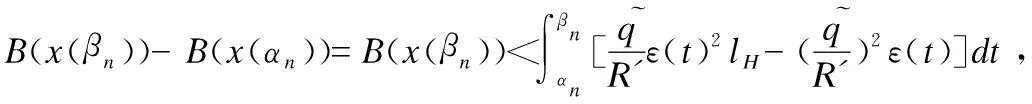
结合情形1和情形2两者均不成立,则下面的情形3一定成立.
情形3.神经网络(2)的解轨迹x(t)会在有限时间内进入到不等式可行域并驻留其中.
注:由定理5及定理2可知,对于任意的初始点x0∈Rn,神经网络(2)的状态解x(t)会在有限时间内进入到可行域Q并驻留其中.
4.5 神经网络收敛到最优解
引理8[17].若x*为优化问题(1)的最优解,则对于任意x∈Q,有ξT(x*-x)≥0,∀ξ(t)∈∂H(x(t)).
定理6.在假设(A)条件下,神经网络(2)至少存在一个最优解,且神经网络(2)从任意点出发,其状态解都收敛到原优化问题(1)的某一个最优解.
证明:由定理5可知进入可行域之后的神经网络模型可化简为:
(24)
其中TQ表示进入可行域Q的时间,因此只需证明对任意初始点x0∈Q,神经网络(2)的解x(t)终会收敛到优化问题(1)的某个最优解.
设x*为原伪凸优化问题的最优解.定义能量函数为:
(25)
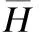
(26)
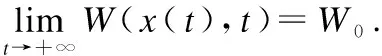
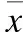
由于∂H(x),∂B(x)是非空紧凸集,存在ξ(tk)∈∂H(x(tk)),γ(tk)∈∂B(x(tk))满足:
(27)
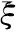
(28)
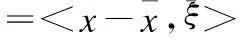
(29)
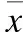
(30)
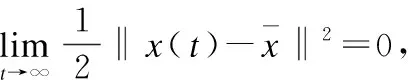
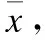
5 数值实验
在本章节中,通过Matlab2012平台模拟神经网络求解优化问题时的性能,验证了神经网络模型(2)解决不等式约束的伪凸优化问题的有效性.
5.1 实验1
考虑下面的非光滑伪凸优化问题:
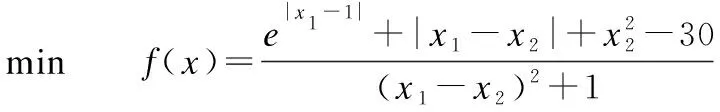
(31)
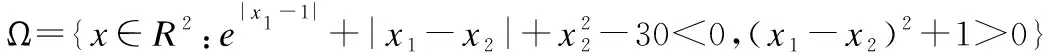
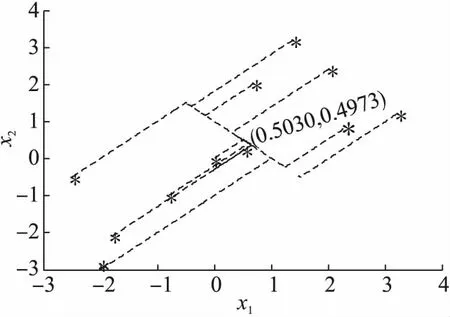
图2 实验1中10个随机初始点关于(x1,x2)的二维相图Fig.2 Two-dimensional phase plot of the trajectories of (x1,x2) with ten random initial in Experiment 1
实验1中神经网络(2)任意选择10个初始点关于(x1,x2)运动轨迹的二维相图.从图中可以看到状态变量从不同初始点出发最终收敛到可行域中一个点Q*=(0.5030,0.4973)T,且不再变化.图3展示了10个不同的初始点对应的目标函数值随着迭代次数向最优解靠近的变化趋势,从图中可以得知目标函数最终收敛到最小点f*=-28.1且不再变化.
5.2 实验2
考虑以下优化问题:
minf(x)=(x1-1)2+(x2-x3)2+(x4-x5)2
s.tx1+x2+x3+x4+x5=5
x3-2x4-2x5=-3
2x1+2x2-x3≤5
x1+3x2≤7
(32)
式(32)是一类常见的优化问题.经计算可知问题(32)存在唯一的最优解x*=(1,1,1,1,1),对应的目标函数最优值为f(x*)=0.文献[8,15]要求初始点在给定区域内;此外,文献[8]需要计算精确的罚因子;文献[16]只能解决等式约束的伪凸优化问题;文献[18]需要获得投影算子,计算麻烦.而本文提出的神经网络模型(2)能克服以上不足且具有良好的性能.在本实验中任意选取初始点为(5,0,-1,3,4),由不等式的定义知其初始点不在可行域内.图4显示了初始点的状态变量随时间变化的趋势,从图中可观察到x(t)的轨迹最终收敛于最优解x*=(1,1,1,1,1).图5给出了迭代点与最优解之间的距离误差分析图,从图中可得知两者之间的误差随着时间的递增趋近于0,说明本文所提出模型能寻找到原始优化问题的最优解.
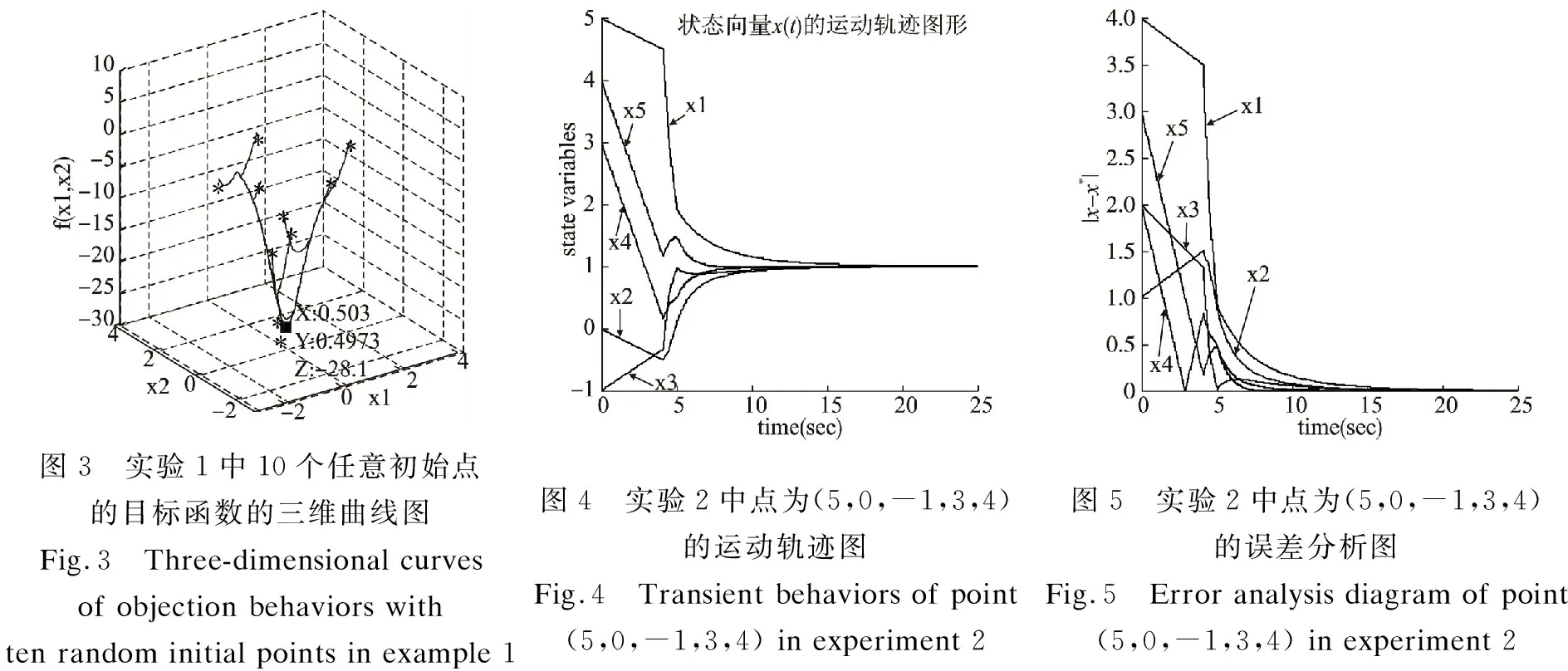
图3 实验1中10个任意初始点的目标函数的三维曲线图Fig.3 Three-dimensional curves of objection behaviors with ten random initial points in example 1图4 实验2中点为(5,0,-1,3,4)的运动轨迹图Fig.4 Transient behaviors of point(5,0,-1,3,4) in experiment 2图5 实验2中点为(5,0,-1,3,4)的误差分析图Fig.5 Error analysis diagram of point(5,0,-1,3,4) in experiment 2
6 结束语
本文中提出了一种新型的递归神经网络模型以解决一类等式约束和不等式约束的伪凸优化问题,与目前所提出的神经网络模型相比,本文使用了正则化的思想,避免了计算惩罚因子的麻烦.同时,还设置了时变控制函数,极大简化了网络模型的复杂度.此外,本文需要较弱的假设条件就可以使神经网络模型的最优解收敛到原伪凸优化问题的最优解中.最后,通过两个仿真实验验证了所提出神经网络模型的有效性.相比现存的神经网络模型,它具有结构简单,不需要计算惩罚因子,初始点可以任意选取及假设条件较宽松的优势.
