基于余弦平顶窗的谐波相量测量

孙冬雪，王江波，姚国盛，李玉鸽

基于余弦平顶窗的谐波相量测量

孙冬雪，王江波，姚国盛，李玉鸽

(中国农业大学信息与电气工程学院，北京 100083)

针对电力系统中带外干扰、频率偏移及其他动态情况下的谐波相量估计问题，提出了一种基于余弦平顶窗的谐波相量估计器。首先基于余弦窗频域表达式，利用理想幅值响应和最小二乘法获得平顶窗的窗系数。在此基础上，为使得滤波器频率响应在标称谐波频率下具有零增益，将所得窗函数与频域采样定理相结合，通过最小二乘法设计一组有限脉冲响应滤波器，用于估计谐波相量。然后，分析了余弦平顶窗和谐波相量测量滤波器的频率响应。最后，采用稳态和动态条件下的不同信号模型对提出的谐波相量估计器进行了性能验证。仿真结果表明，相对于基于Sinc插值函数和频域采样定理的两种谐波相量估计器，所提方法有较强的带外干扰抑制能力，在多种条件下能实现较高精度的谐波相量测量。

谐波相量测量；余弦平顶窗；最小二乘法；频域采样；综合矢量误差

0 引言

双碳目标下新能源发电快速发展，非线性电力电子设备和元件在电网中的广泛使用加重了电网谐波污染[1-5]。谐波频率、幅值和相位等参数的实时、快速和准确的测量是谐波监测、评估和治理的基础，为改善电网电能质量，保证电力系统安全稳定运行提供依据。同时，谐波的高精度测量是电网保护设备的数字算法实现、谐波潮流计算以及电力设备绝缘检测等应用的前提和基础[9-10]。

国内外学者提出了多种谐波相量测量算法，离散傅里叶变换(discrete fourier transform, DFT)算法是谐波相量测量常用的方法之一。但DFT 是一种静态谐波估计技术，在非标称频率及动态条件下，频谱泄露和栅栏效应会使估计误差增大[11-12]。为解决此问题，文献[13]提出一种多谱线插值快速傅里叶变换(fast fourier transform, FFT)方法，不需要利用性能较好的窗函数即可实现对长、短范围泄漏效应的修正，具有广泛的适用性。文献[14]利用一种基于多谱线插值法和复调制细化法的组合分析方法，以提高谐波分析的准确性。插值算法在很大程度上提高了谐波估计精度，但有限的采样周期使谐波分析的分辨率不足以实现在更相近频域内准确检测谐波和间谐波。

近年来，小波变换及其改进算法也被应用于谐波检测。文献[15]提出了4种多频带小波函数及其相应的多频带小波变换方法。文献[16]结合DFT和小波包变换的优秀特性，提出了一种能够提高谐波检测实时性的综合谐波检测方法。文献[17]利用基于经验小波变换的方法解决噪声干扰下的稳态及暂态谐波检测问题。小波变换具有多尺度时频分辨能力，适合分析动态和瞬变信号，但混叠现象和合适小波基的选取给精确测量带来很大难度[18]。

文献[19]提出了重构递归最小二乘技术用于相量和谐波的实时估计，但该方法计算复杂，对硬件设备要求高。文献[20]利用旋转不变性技术估计谐波相量，减少谐波间干扰，提高谐波相量估计精度，但处理时间会随信号中谐波分量的增加而延长。文献[21]通过基于RBF的神经网络进行电力系统谐波检测，提高检测精度和实时性，但该方法计算相对复杂，难以在硬件上实现。

平顶有限脉冲响应(finite impulse response, FIR)滤波器是最近谐波估计的热点方法。文献[22]在FFT的基础上设计了一个平顶FIR滤波器，估计在观测窗口内随时间变化的谐波。文献[23]利用基于泰勒的带通滤波器估计谐波参数，提高标称和非标称频率下的谐波测量精度，降低计算复杂度。文献[24]利用一种平顶FIR滤波器估计50次谐波相量，适用于在有附加噪声的稳态和动态条件下。文献[25]基于Sinc插值函数设计了一组FIR滤波器用于谐波相量估计。文献[26-27]提出了一种基于频域采样定理的谐波相量估计器。这些方法在电网频率偏移、调制振荡等干扰条件下具有较强的谐波抑制能力，但抗带外干扰能力较差是其无法避免的问题。

为解决上述问题，提出了基于余弦平顶窗的谐波相量估计器，根据余弦窗函数的频域表达式和理想幅值响应值计算出平顶窗函数系数，通过平顶窗函数与频域采样定理结合，利用最小二乘法得到谐波相量测量滤波器。该滤波器频率响应具有平顶窗函数平坦主瓣特性和旁瓣在谐波频率处零增益的特性，同时在带外干扰频率处衰减尤为明显，在确保谐波测量精度的同时，具有较强的抗带外干扰能力。

1 滤波器设计

对于工频电力系统而言，电压电流实时波形通过DFT分析后得到一系列频谱分量，通常将这些频谱分量中工频整数倍的频谱分量定义为谐波[28]。谐波信号被定义为

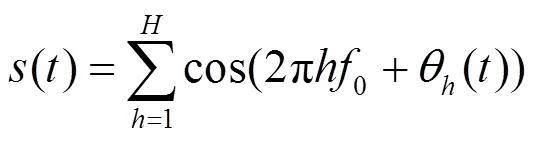
1.1 余弦平顶窗函数设计

余弦窗窗函数可以表示为

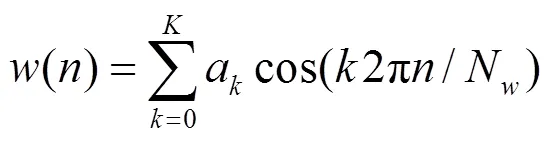
该窗函数幅值响应通过插值函数[29]表示为

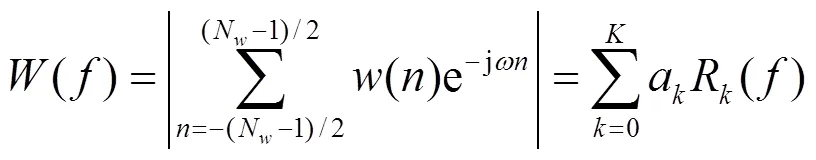
式(4)可以用相对频率表示为

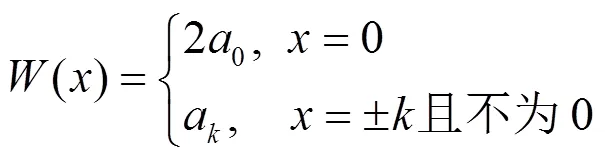
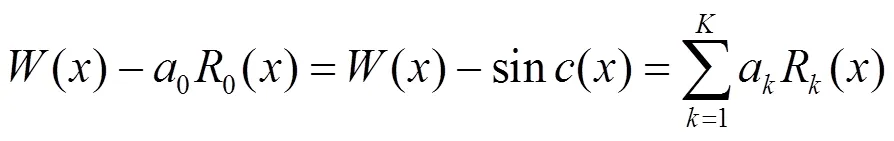
式(7)表示成矩阵形式为

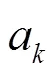
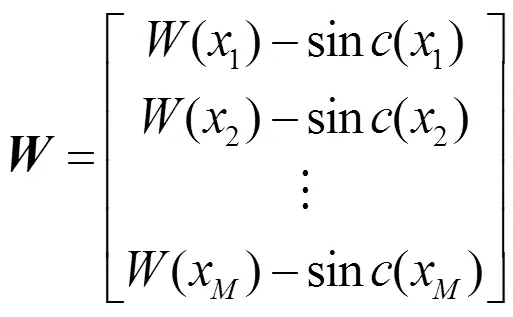
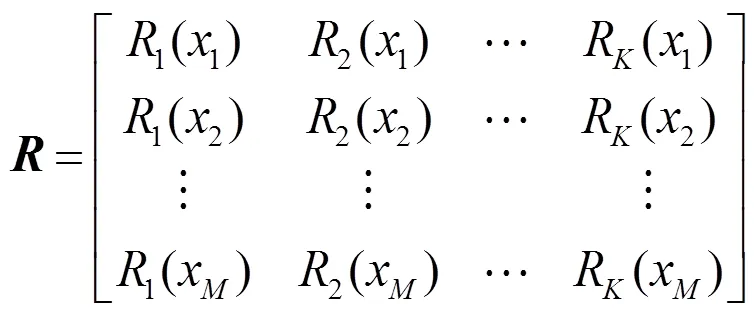
如果＞，向量可通过最小二乘算法计算得到：

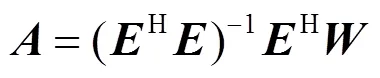
1.2 谐波相量测量算法

文献[27]中提出的谐波相量估计器(harmonic phasor estimator, HPE)基于频域采样定理，在标称谐波频率下具有零误差结果。所以，为了提高滤波器频率响应在谐波频率处的衰减能力，将所设计的CFW结合频域采样定理，窗系数与虚指数函数组成矩阵，通过最小二乘法进行计算。

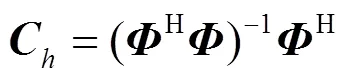
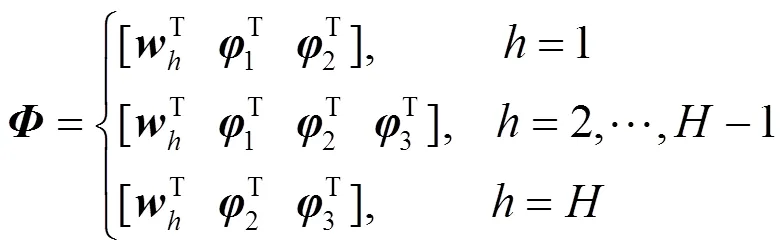
2 性能分析

2.1 余弦平顶窗函数频率响应

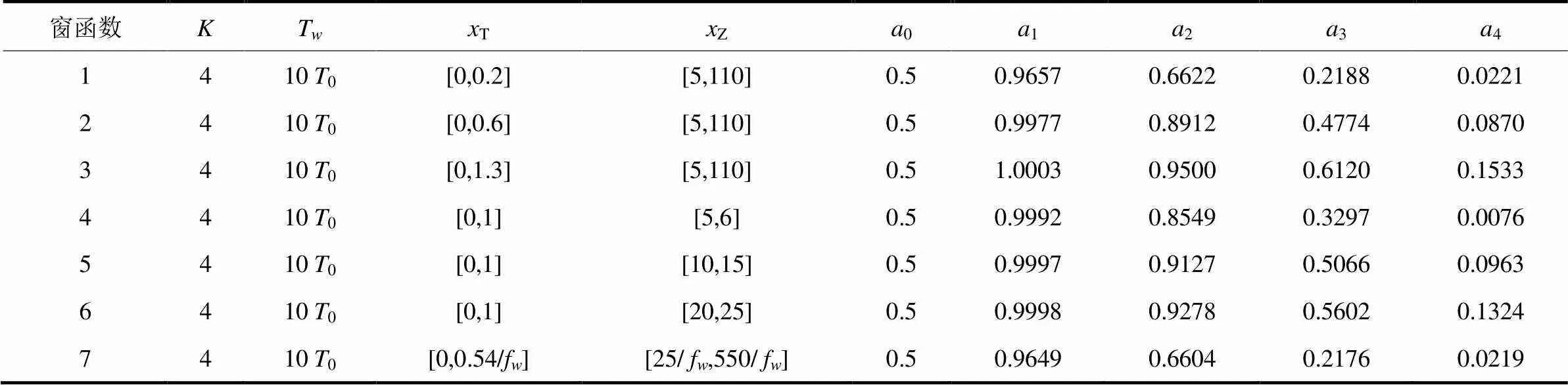
表1 不同CFW的窗函数系数值

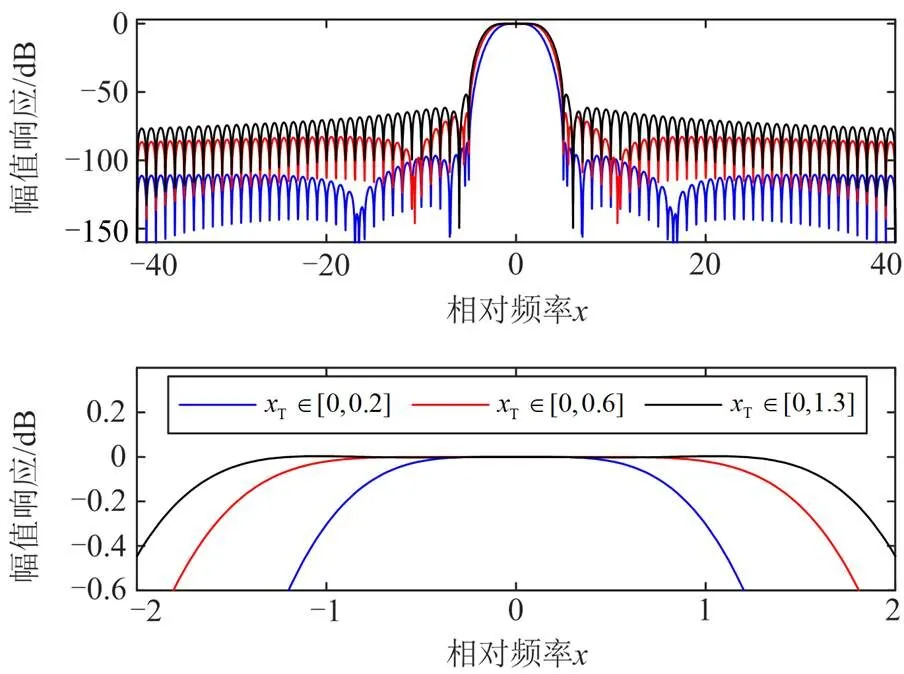
图1 通带范围变化的幅值响应

图2 阻带范围变化的幅值响应

2.2 谐波相量测量滤波器性能对比

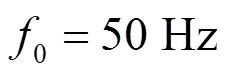
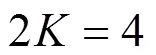
综上所述，将所设计的平顶窗与频域采样定理相结合用于谐波相量测量滤波器的设计，提出的谐波相量测量滤波器同时具有较平坦的通带和较低的阻带，并具有很强的特定谐波抑制能力和抗带外干扰能力。

3 性能验证

为了进一步验证和对比3种方法的性能，使用上述滤波器参数设置，参考文献[32]中指定的同步相量测量基准，在同一条件下进行以下稳态和动态仿真实验，以综合矢量误差(total vector error, TVE)为评价指标评价上述3种方法的性能。

3.1 阶跃响应时间测试

测量响应时间是指在信号输入施加阶跃变化时，测量值超出指定精度限制对应的时刻到测量值重新进入并保持在该精度限制内的时刻，这两者之间持续的时间差。

幅值阶跃和相位阶跃信号如下：

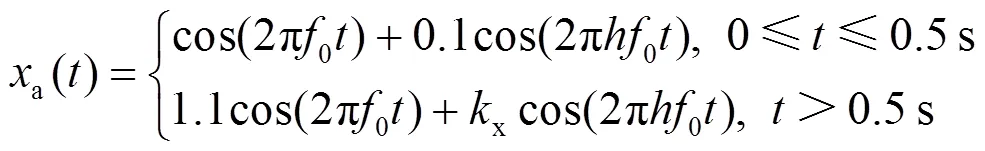
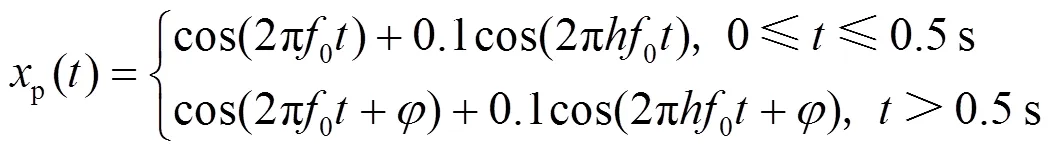
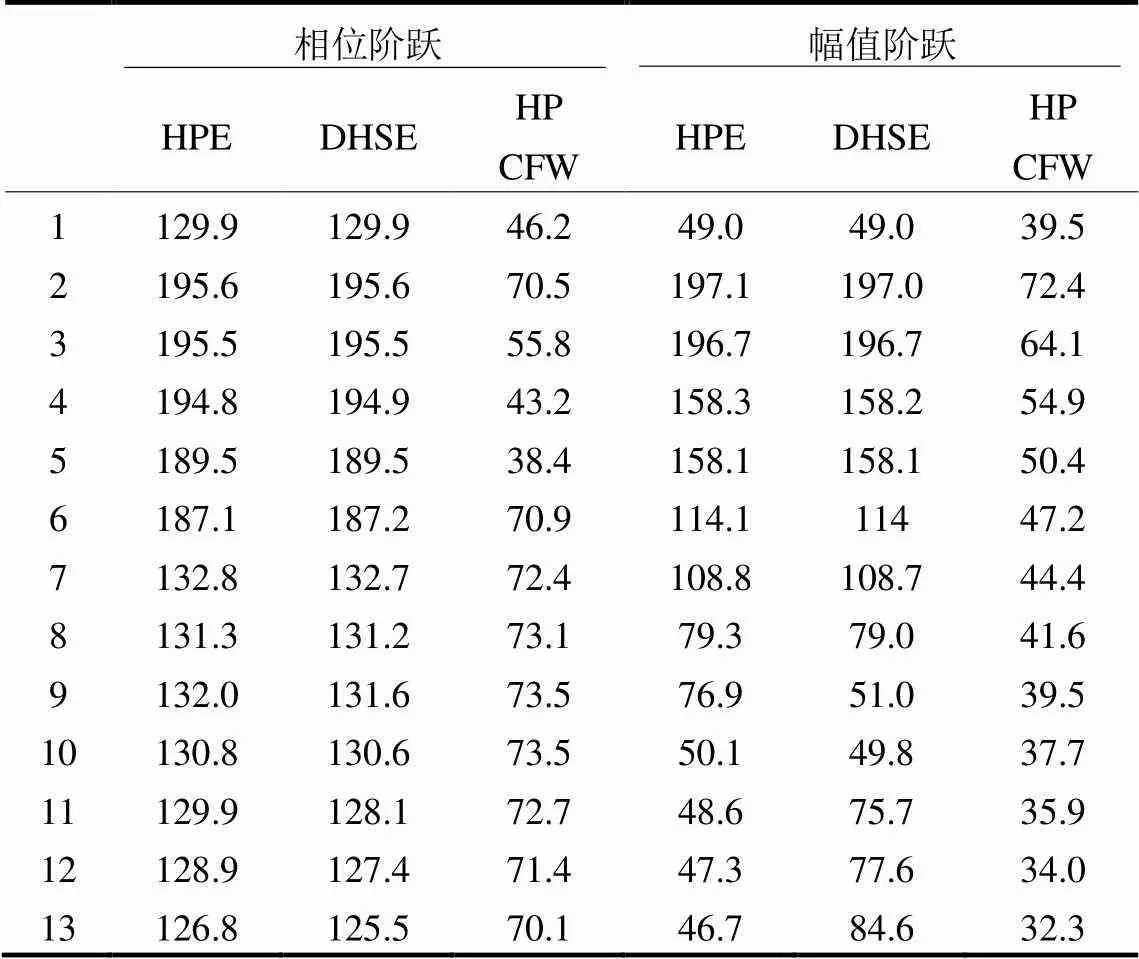
表2 阶跃变化情况下的响应时间

3.2 测量精度测试

1) 单次谐波实验

输入电网信号为理想正弦波，其中包含基波和次谐波。

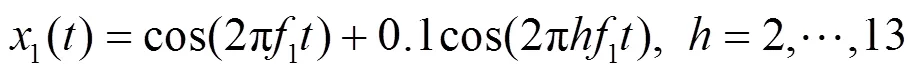
2) 噪声干扰

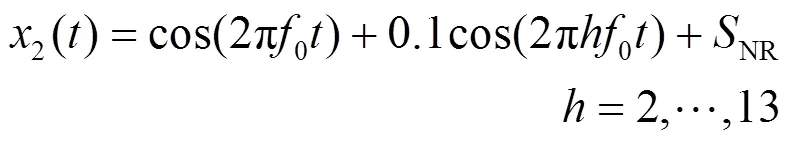
式中，为信噪比，单位为dB。

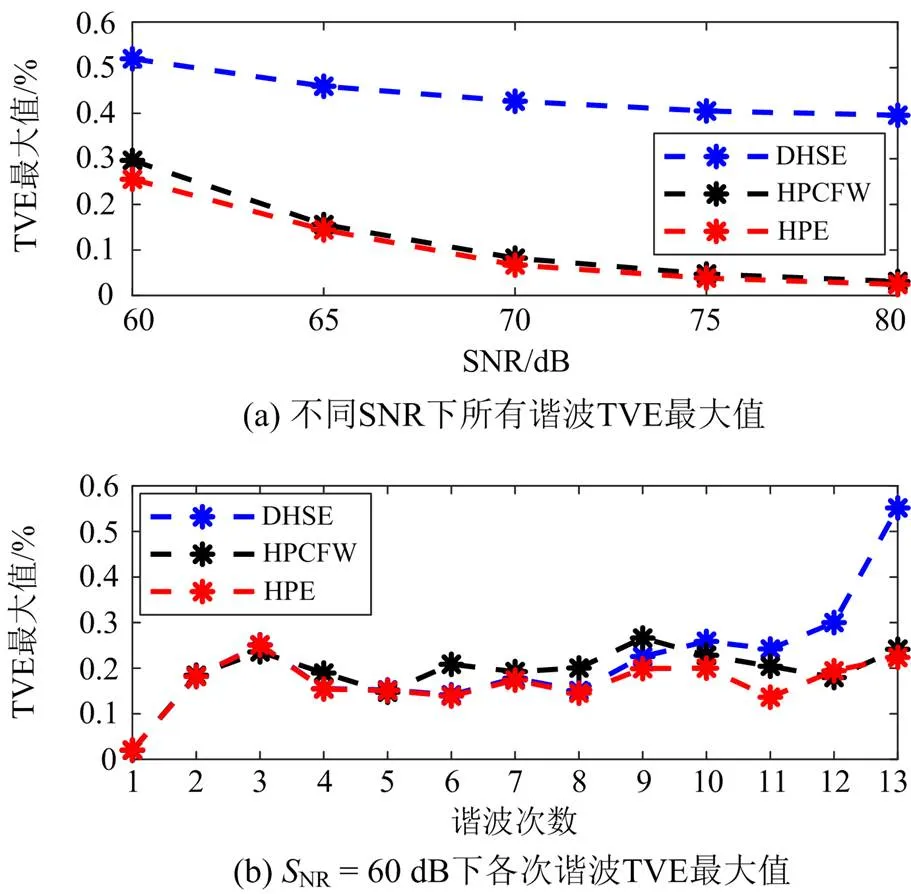
图5 噪声干扰测试结果

3) 多重谐波干扰

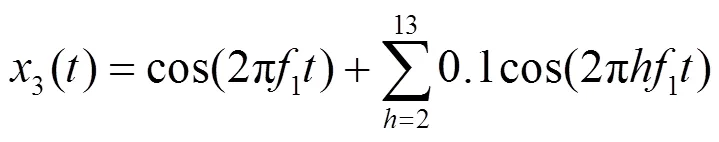
式中，为谐波次数，将10%的2～13次谐波均加入到基波信号中作为输入信号。

图6 多重谐波干扰测试结果

4) 频率斜坡

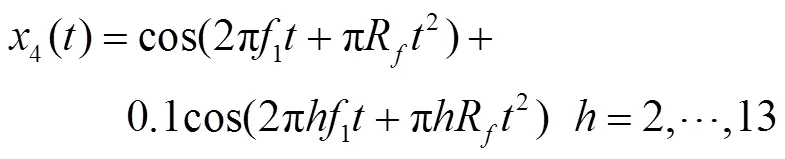
频率斜波测试结果如图7所示。1 s内基波频率从49.5 Hz线性变化到50.5 Hz，各次谐波的TVE最大值如图7(a)所示，13次谐波的TVE结果如图7(b)所示。从图7中可以看出，6次及以下谐波时，3种方法的测量误差均在0.1%以下，7次谐波之后，随着谐波次数的升高，DHSE和HPE的谐波相量测量误差显著增大，最大误差分别为2.741%和3.048%，而HPCFW的最大TVE为0.2174%；在不同基波频率下，HPE和DHSE对各次谐波的测量误差有波动，而HPCFW的估计误差波动很小且误差低。结果证明，本文提出的方法在基波频率线性增长情况下的测量精度也能满足要求。

5) 相位调制和幅值调制

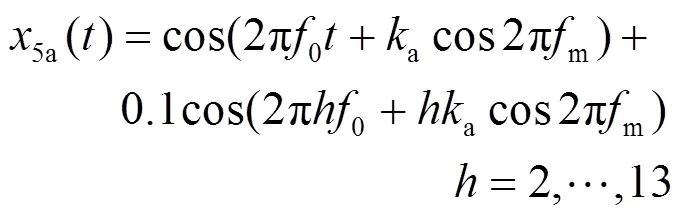
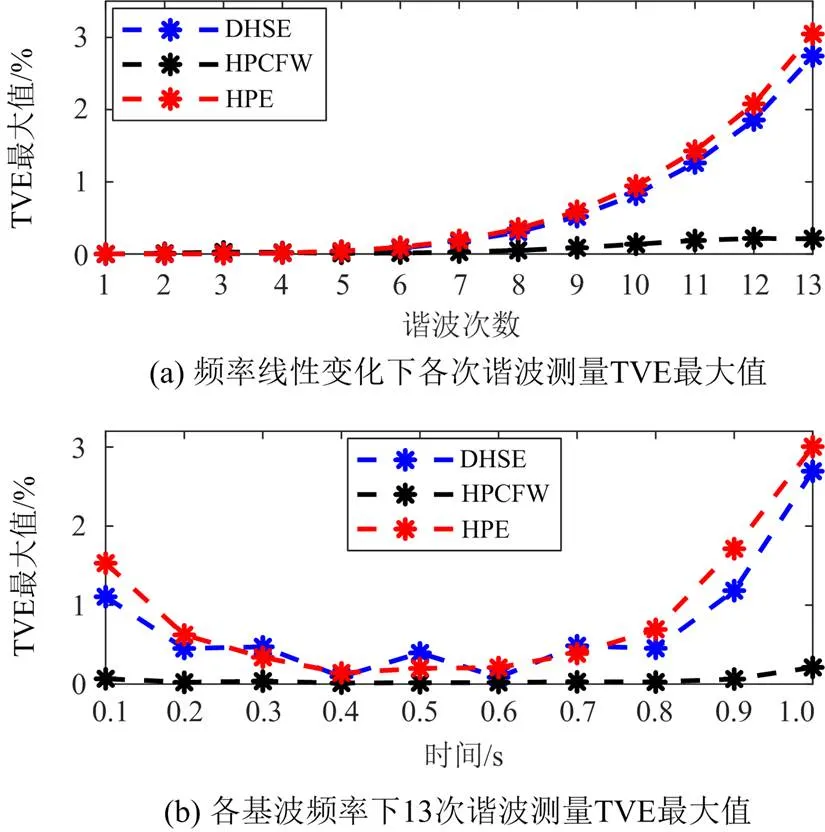
图7 频率斜坡测试结果

调制测试结果如图8所示。各次谐波次数下幅值调制和相位调制的TVE最大值分别如图8(a)、图8 (b)所示。从图8中可以看出，在两种情况下，HPCFW的谐波相量测量精确度均高于DHSE和HPE，尤其在相位调制条件下，随着谐波次数的升高，DHSE和HPE的测量误差明显变大，最大值达到了14.23%和15.37%，而本文方法的误差均小于3%，所以在调制测试中，HPCFW也表现出了良好的测量性能。

图8 调制测试结果

6) 带外干扰

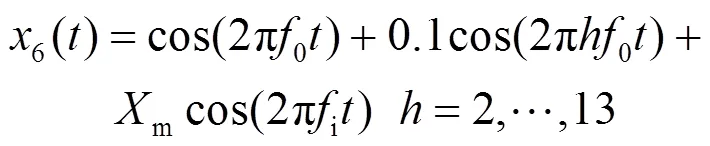
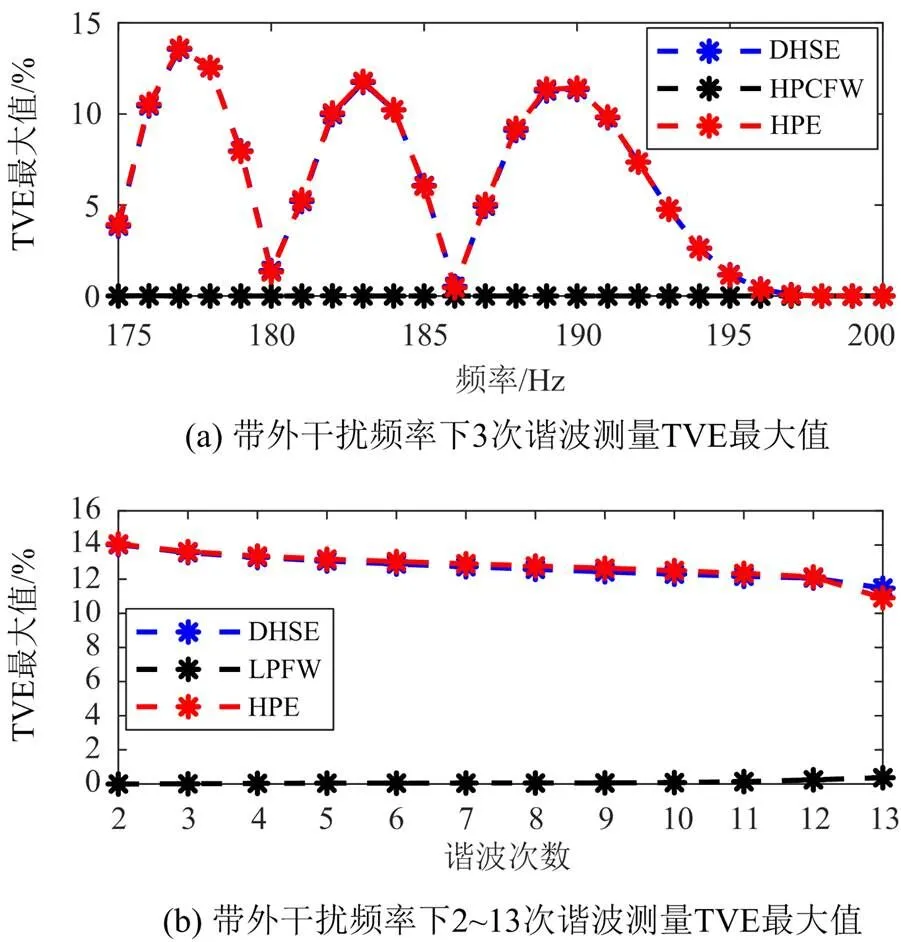
图9 带外干扰测试结果

4 结论

本文提出了一种基于余弦平顶窗的谐波相量测量估计器，通过窗函数理想幅值响应和频域采样定理改善窗函数主瓣平坦和旁瓣衰减特性，从而得到具有更好谐波相量估计性能的FIR滤波器。该滤波器与HPE相似，计算过程简单，无需占用很多内存资源，可以适应谐波频率具有带宽变化的特点，根据基频带宽选择模型参数，可以平坦主瓣，在谐波和带外干扰频率处旁瓣衰减低，能够弥补HPE和DHSE在带外干扰条件下谐波相量估计的不足。仿真对比分析表明，HPCFW在多种情况下都有良好的谐波相量测量效果，在有多次谐波干扰并发生频率偏移、相位调制、幅值调制和存在带外干扰的情况下，提出方法的谐波相量估计精度明显高于DHSE和HPE，在信号中存在带外干扰时更为突出。本文方法能有效抑制间谐波干扰，对于间谐波相关参数的测量是下一步的研究内容。

[1] 文劲宇, 周博, 魏利屾. 中国未来电力系统储电网初探[J]. 电力系统保护与控制, 2022, 50(7): 1-10.

WEN Jinyu, ZHOU Bo, WEI Lishen. Preliminary study on an energy storage grid for future power system in China[J]. Power System Protection and Control, 2022, 50(7): 1-10.

[2] 李晓娜, 沈兴来, 薛雪, 等. 基于改进HHT和决策树的电能质量扰动辨识[J]. 电力建设, 2017, 38(2): 114-121.

LI Xiaona, SHEN Xinglai, XUE Xue, et al. Power quality disturbance identification based on improved HHT and decision tree[J]. Electric Power Construction, 2017, 38(2): 114-121.

[3] CASRTELLO P, LAURANO C, MUSCAS C, et al. Harmonic synchrophasors measurement algorithms with embedded compensation of voltage transformer frequency response[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 1-10.

[4] 刘灏, 许苏迪, 毕天姝, 等. 基于同步相量数据的间谐波还原算法[J]. 电力自动化设备, 2019, 39(1): 153-160.

LIU Hao, XU Sudi, BI Tianshu, et al. Inter-harmonic reduction algorithm based on synchrophasor measurements[J]. Electric Power Automation Equipment, 2019, 39(1): 153-160.

[5] 邵振国, 许昊铂, 肖颂勇, 等. 新能源电网中的谐波问题[J]. 电力系统保护与控制, 2021, 49(4): 178-187.

SHAO Zhenguo, XU Haobo, XIAO Songyong, et al. Harmonic problems in a new energy power grid[J]. Power System Protection and Control, 2021, 49(4): 178-187.

[6] 熊杰锋, 李群, 袁晓冬, 等. 电力系统谐波和间谐波检测方法综述[J]. 电力系统自动化, 2013, 37(11): 125-133.

XIONG Jiefeng, LI Qun, YUAN Xiaodong, et al. Detection methods of harmonics and inter-harmonics in power systems[J]. Automation of Electric Power Systems, 2013, 37(11): 125-133.

[7] 张佳怡, 符玲, 熊思宇, 等. 计及频率偏移的动态谐波相量测量算法[J]. 中国电机工程学报, 2017, 37(8): 2270-2279.

ZHANG Jiayi, FU Ling, XIONG Siyu, et al. Dynamic harmonic phasor measurement algorithm considering frequency deviation[J]. Proceedings of the CSEE, 2017, 37(8): 2270-2279.

[8] RAKPENTHAI C, UATRONGIT S, WATSON N R, et al. On harmonic state estimation of power system with uncertain network parameters[J]. IEEE Transactions on Power Systems, 2013, 28(4): 4829-4838.

[9] 李振华, 胡廷和, 杜亚伟, 等. 基于窗函数和谱线插值理论的谐波检测方法[J]. 电力系统保护与控制, 2019, 47(22): 78-88.

LI Zhenhua, HU Tinghe, DU Yawei, et al. Harmonic detection method based on the theory of windows and spectrum line interpolation[J]. Power System Protection and Control, 2019, 47(22): 78-88.

[10] KUŠLJEVIĆ M D, TOMIĆ J J, POLJAK P D. Maximally flat-frequency-response multiple-resonator-based harmonic analysis[J]. IEEE Transactions on Instrumentation and Measurement, 2017, 66(12): 3387-3398.

[11] 郭成, 尹轲, 张艳萍, 等. 一种基于综合DFT和Prony算法的谐波与间谐波分析方法[J]. 电力系统保护与控制, 2021, 49(17): 1-9.

GUO Cheng, YIN Ke, ZHANG Yanping, et al. A harmonic and interharmonic analysis method based on integrated DFT and Prony algorithm[J]. Power System Protection and Control, 2021, 49(17): 1-9.

[12] RADULOVIĆ M, ZEČEVIĆ Ž, KRSTAJIĆ B. Dynamic phasor estimation by symmetric Taylor weighted least square filter[J]. IEEE Transactions on Power Delivery, 2020, 35(2): 828-836.

[13] 吴静, 赵伟. 一种用于分析电网谐波的多谱线插值算法[J]. 中国电机工程学报, 2006, 26(8): 55-60.

WU Jing, ZHAO Wei. An algorithm of MICA for analyzing harmonics in power system[J]. Proceedings of the CSEE, 2006, 26(8): 55-60.

[14] 赵帅旗, 肖辉, 李文俊, 等. 基于多谱线插值法和复调制细化法的电力系统谐波分析[J]. 电测与仪表, 2019, 56(18): 10-15, 24.

ZHAO Shuaiqi, XIAO Hui, LI Wenjun, et al. Harmonic analysis of power system based on multi-spectral interpolation and complex modulation[J]. Electrical Measurement & Instrumentation, 2019, 56(18): 10-15, 24.

[15] 任震, 黄群古, 黄雯莹, 等. 基于多频带小波变换的电力系统谐波分析新方法[J]. 中国电机工程学报, 2000, 20(12): 39-42.

REN Zhen, HUANG Qungu, HUANG Wenying, et al. New methods of power system harmonic analysis based on wavelet transform with multi-frequency band[J]. Proceedings of the CSEE, 2000, 20(12): 39-42.

[16] 房国志, 杨超, 赵洪. 基于FFT和小波包变换的电力系统谐波检测方法[J]. 电力系统保护与控制, 2012, 40(5): 75-79.

FANG Guozhi, YANG Chao, ZHAO Hong. Detection of harmonic in power system based on FFT and wavelet packet[J]. Power System Protection and Control, 2012, 40(5): 75-79.

[17] 吴建章, 梅飞, 陈畅, 等. 基于经验小波变换的电力系统谐波检测方法[J]. 电力系统保护与控制, 2020, 48(6): 136-143.

WU Jianzhang, MEI Fei, CHEN Chang, et al. Harmonic detection method in power system based on empirical wavelet transform[J]. Power System Protection and Control, 2020, 48(6): 136-143.

[18] ZHAO Wenjing, SHANG Liqun, SUN Jinfan. Power quality disturbance classification based on time-frequency domain multi-feature and decision tree[J]. Protection and Control of Modern Power Systems, 2019, 4(4): 337-342.

[19] SADINEZHAD I, AGELIDIS V G. Real-time power system phasors and harmonics estimation using a new decoupled recursive-least-squares technique for DSP implementation[J]. IEEE Transactions on Industrial Electronics, 2013, 60(6): 2295-2308.

[20] JAIN S K, JAIN P, SINGH S N. A fast harmonic phasor measurement method for smart grid applications[J]. IEEE Transactions on Smart Grid, 2017, 8(1): 493-502.

[21] 肖建平, 李生虎, 吴可汗, 等. 一种新的基于神经网络的电力系统谐波检测方法研究[J]. 电工技术学报, 2013, 28(增刊2): 345-348.

XIAO Jianping, LI Shenghu, WU Kehan, et al. A novel approach of harmonic detection in power system based on neural network[J]. Transactions of China Electrotechnical Society, 2013, 28(S2): 345-348.

[22] PLATAS M A, ADLO J. Dynamic harmonic analysis through Taylor-Fourier Transform[J]. IEEETransactions on Instrumentation and Measurement, 2011, 60(3): 804-813.

[23] ZEČEVIĆ Ž, KRSTAJIĆ B. Dynamic harmonic phasor estimation by adaptive Taylor-based bandpass filter[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 21-29.

[24] DUDA K, ZIELIŃSKI T P, BIEŃ A, et al. Harmonic phasor estimation with flat-top FIR filter[J]. IEEE Transactions on Instrumentation and Measurement, 2020, 69(5): 2039-2047.

[25] CHEN Lei, ZHAO Wei, WANG Qing, et al. Dynamic harmonic synchrophasor estimator based on Sinc interpolation functions[J]. IEEE Transactions on Instrumentation and Measurement, 2019, 68(9): 3054-3065.

[26] CHEN Lei, ZHAO Wei, ZHAO Dongfang, et al. Frequency-domain sampling theorem-based harmonic phasor estimator[C] // 2020 Conference on Precision Electromagnetic Measurements (CPEM), August 24-28, 2020.

[27] CHEN Lei, ZHAO Wei, XIE Xiaorong, et al. Harmonic phasor estimation based on frequency-domain sampling theorem[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 11-20.

[28] 西安领步电能质量研究所, 深圳市领步科技有限公司, 中国电力科学研究院, 等. 电能质量公用电网间谐波: GB/T 24337—2009[S]. 北京: 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会, 2010.

[29] 程佩青. 数字信号处理教程[M]. 北京: 清华大学出版社, 2017.

[30] 中国电力科学研究院, 南方电网超高压输电公司, 广东电网公司电力科学研究院, 等. 电磁兼容试验和测量技术供电系统及所连设备谐波、间谐波的测量和测量仪器导则[S]. 北京: 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会, 2017.

[31] IEC international standard—electromagnetic compatibility—part 4-7: testing and measurement techniques—general guide on harmonics and interharmonics measurements and instrumentation, for power supply systems and equipment connected thereto: IEC 61000-4-7 edition 2.1—2009[S]. 2009.

[32] IEEE/IEC international standard—measuring relays and protection equipment—part 118-1: synchrophasor for power systems—measurements: IEC/IEEE 60255-118- 1—2018[Z]. 2018.

Harmonic phasor measurement based on a cosine flat-top window

SUN Dongxue, WANG Jiangbo, YAO Guosheng, LI Yuge

(College of Information and Electrical Engineering, China Agricultural University, Beijing 100083, China)

There is a problem of harmonic phasor estimation under out-of-band interference, frequency deviation and other dynamic situations in power systems. Thus a harmonic phasor estimator based on a cosine flat-top window is proposed. First, the window coefficients of the flat-top window are obtained by the ideal amplitude response and the least squares method based on the cosine window frequency domain expression. To obtain a frequency response with zero gain at the nominal harmonic frequency, the obtained window function is combined with the frequency domain sampling theorem. Based on this, a bank of finite impulse response filters is designed by the least squares method, and they are used to estimate the harmonic phasor. Then, the frequency response of the cosine flat-top window and the harmonic phasor measurement filter is analyzed. Finally, the performance of the proposed harmonic phasor estimator is verified by different signal models under steady-state and dynamic conditions. The simulation results show that, compared with the two harmonic phasor estimators based on the Sinc interpolation function and the frequency domain sampling theorem, the proposed method has a stronger ability to suppress out-of-band interference, and more accurate harmonic phasor estimation can be realized under thevarious conditions.

harmonic phasor measurement; cosine flat-top window; least squares method; frequency-domain sampling; total vector error

10.19783/j.cnki.pspc.220468

国家自然科学基金项目资助(51477173)

This work is supported by the National Natural Science Foundation of China (No. 51477173).

2022-04-03；

2022-07-20

孙冬雪(1998—)，女，硕士，主要研究方向为电能质量检测，同步相量、谐波的检测与分析等；E-mail: sundongxue@ cau.edu.cn

王江波(1978—)，男，通信作者，博士，副教授，主要研究方向为电力系统测量与控制，配电自动化技术；E-mail: jiangbowang@cau.edu.cn

姚国盛(1996—)，男，硕士，主要研究方向为电能质量检测，同步相量、谐波的检测与分析等。E-mail: S20193081354@cau.edu.cn

(编辑 许 威)