改进EGM模型对特高压输电线路的适用性与验证

杨明浩，安韵竹，胡元潮，李志军，冯守信

改进EGM模型对特高压输电线路的适用性与验证

杨明浩1，安韵竹1，胡元潮1，李志军2，冯守信1

(1.山东理工大学电气与电子工程学院，山东 淄博 255000；2.中国电力科学研究院，湖北 武汉 430074)

为了更准确地分析我国特高压输电线路雷电绕击屏蔽性能，基于我国长空气间隙放电试验数据和雷电回击观测数据，建立考虑地形条件的适应于大尺寸输电线路雷电屏蔽性能评估的改进电气几何模型(electric geometry model, EGM)并进行验证，将击距公式修正为s= 0.13(2+ 40)0.814。改进EGM模型对超、特高压输电线路三相导线的雷电绕击率计算结果与日本实际线路雷击观测数据及我国平原、山区特高压输电线路雷击模拟试验数据具有一致性，验证了改进EGM模型的适用性。采用改进EGM模型评估了杆塔型式、山坡陡度对我国特高压线路绕击跳闸率的影响。计算结果表明，采用SZ322型杆塔的绕击跳闸率高于采用SZT1型杆塔，且特高压线路绕击跳闸率随山坡陡度的增大而增大。EGM模型的修正以及计算方法的优化，对我国特高压输电线路雷电屏蔽性能的设计具有一定的指导意义。

特高压输电线路；雷电屏蔽模拟试验；电气几何模型(EGM)；击距公式

0 引言

在实现碳达峰、碳中和目标的大背景下，我国为满足风能、太阳能等清洁能源大规模开发和消纳的需要，特高压的建设也在加速进行中。大尺寸输电线路暴露在自然环境中，在雷雨季节容易遭受雷击[1-4]。我国1000 kV输电线路都榕线分别在2015年和2017年发生雷电绕击跳闸故障，此外我国±800 kV输电线路宾金线、复奉线和锦苏线自2010年以来发生雷电绕击故障10余次[5]。特高压输电线路输电容量大、损耗低，但相比220 kV及以下等级输电线路更易发生雷电绕击事故，并且事故造成的危害及损失也更大。国内外相关行业运行经验也已表明，当前特高压输电线路雷击跳闸故障的产生原因主要以雷电绕击为主，造成这一问题的原因之一是目前特高压输电线路雷电屏蔽系统的设计借鉴较低电压等级输电线路的计算模型，导致了较大的计算误差。因此，研究适应于大尺寸特高压输电线路雷电屏蔽性能的评估模型是十分必要的。

电气几何模型(electric geometry model, EGM)法主要用于输电线路绕击性能研究，被世界各国电力企业、IEC和IEEE等国际组织广泛采用。自1961年文献[6]提出雷电回击模型的概念以来，不断有学者尝试通过各种方式改进击距公式，1968年文献[7]首次利用实验室1～3 m间隙放电试验提出了经典EGM模型，此后在此基础上很多学者对经典EGM模型作了进一步改进，使得输电线路雷电屏蔽性能的评估更具有适用性。1985年，IEEE工作组综合各种因素提出通用击距公式和击距系数[8]，这些通过1～4 m间隙距离放电试验数据改进而来的击距公式，在较低电压等级输电线路雷电屏蔽性能中起到了重要的指导作用。而随着输电线路电压等级的提高，特别是特高压交直流输电技术的快速发展，空气间隙进一步加长，对于特高压输电线路绕击跳闸率过高和某些在理论模型上处于完全屏蔽线路的屏蔽失效情况，使用传统EGM模型方法已不能很好地解释。

近年来，国内外学者开始尝试将输电线路运行经验和更长间隙放电实验数据结合起来，对EGM模型中的击距公式和击距系数进行改进，便于评估大尺寸特高压交流输电线路绕击特性。EGM模型中击距公式是由间隙放电试验和雷电观测经验公式共同推导出来的，因此相关雷电经验公式的准确性也影响着模型的精确度。日本学者Taniguchi等于2008年进行了最大间隙距离为6 m的间隙放电试验，结合回击速度概率公式对EGM模型进行了改进[9]。武汉大学于2014年为研究负极性操作冲击电压下典型长空气间隙的放电特性，利用-20/2500 μs、-80/2500 μs两种电压波形，开展了间隙距离最大达到10 m的负极性放电特性试验，得到了1～10 m空气间隙的放电特性[10-11]。2015年，武汉大学又开展了缩比为1:12.5的特高压交流输电线路雷击特性模拟试验，获得了实验室条件下特高压输电线路的雷击特性[12]。上述大尺寸放电试验为研究适应于特高压输电线路的EGM模型中击距公式和击距系数的修正提供了基础数据。此外，目前绝大多数文献在进行击距公式修正时，采用的主放电电流与主放电速度1的关系式为经大量理论分析估算的经验公式=240013[5]。文献[14]通过开展人工引雷实验发现继后回击的速度与其电流峰值有较好的非线性相关性。文献[13]利用大尺寸长空气间隙放电数据与人工引雷先导通道回击速度的概率分布[14]相结合，提出了与雷电回击速度相关的改进击距公式。由于该击距公式与回击速度的分散概率相关，因此击距公式为与回击速度相关的分散形式。然而，实际雷击过程随机性强，雷电回击速度并非仅包含其分散形式中考虑的有限个雷电回击速度。文献[14]的相关研究表明，人工引雷先导通道回击速度的概率分布规律符合文献[15]所推荐使用的回击速度与电流峰值之间的关系式。由于文献[15]提出的回击速度与雷电流峰值关系式能够与实验室人工引雷实验数据相互验证，可利用该关系式将EGM模型中击距公式修正为只与回击电流幅值相关的表达式。

鉴于此，本文将大尺寸长空气间隙负极性放电特性的数据与文献[15]提出的回击速度与雷电流峰值的关系式相结合，对EGM模型中击距公式和击距系数这两个关键参数分别进行修正；将本文改进EGM模型的雷电绕击率计算结果与日本超特高压输电线路的雷电观测数据对比，验证本文改进EGM模型对大尺寸输电线路雷电绕击率评估的适应性；结合特高压输电线路雷电屏蔽性能模拟试验，分析地形条件对特高压输电线路雷电屏蔽性能的影响规律，并与本文改进EGM模型计算结果进行对比；最后，考虑到我国线路雷电屏蔽性能受地形条件影响较大[16-17]，且我国1000 kV输电线路所架设杆塔型式多样[18]，采用改进EGM模型计算分析杆塔构型、山坡陡度对我国特高压输电线路雷电屏蔽性能的影响。本文研究工作可为特高压输电线路的雷电屏蔽性能的设计提供参考。

1 长间隙放电与自然雷电数据结合的电气几何模型修正

1.1 击距公式与击距系数的修正

1.1.1雷电先导头部电位的简化表达

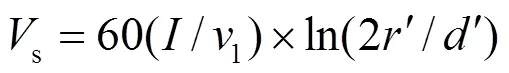
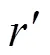
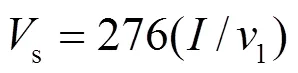
文献[14]通过开展人工引雷实验发现继后回击的速度与其电流峰值有较好的非线性相关性。其研究结果基本上验证了Lundnolm所推荐使用的回击速度与电流峰值之间的关系式，如式(3)所示[15]。

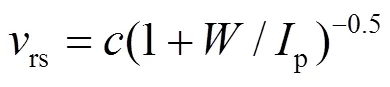
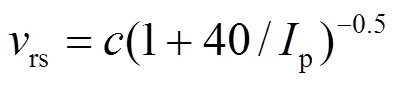
1.1.2结合长间隙放电试验数据的击距公式修正

文献[10]中1～10 m棒-棒间隙50%放电电压与间隙距离关系如式(5)所示。

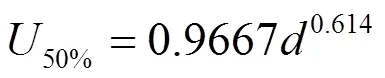
将式(4)代入式(2)，可得主放电电流与先导电压s的关系式如式(6)所示。

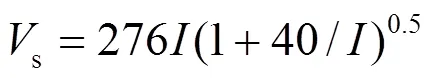
联立式(5)和式(6)，将棒-棒间隙的50%放电电压与雷电先导最后一击时头部电位看作相等，可得到改进后的击距公式如式(7)所示。

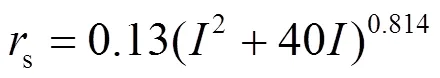
本文改进击距公式(7)与先前学者提出的击距公式对比如图1所示。在雷电流幅值小于40 kA时，同一雷电流幅值下本文改进后的击距小于大部分学者提出的击距；而在雷电流幅值超过80 kA时，本文改进后击距较大。

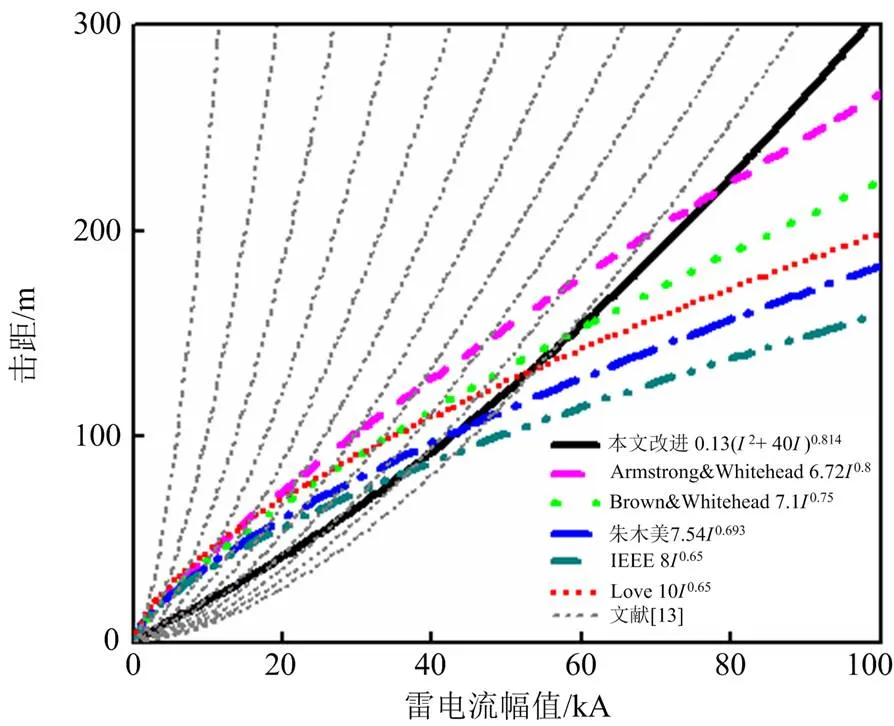
图1 修正击距公式与先前击距公式对比图

1.1.3击距系数的选取

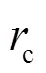
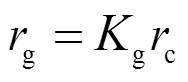
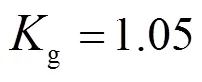
1.2 EGM修正模型计算方法

EGM模型中认为由雷电先导向大地发展的先导放电通道的头部在到达被击物体的临界击穿距离(即击距)之前，击中点是不确定的，先导到达哪个物体的击距之内，即向该物体放电。同时传统的EGM模型认为，雷电先导是垂直下落的，而这与实际情况并不相符[24]，因此本文考虑了雷电先导在(-π/2, π/2)内入射的概率分布，如式(10)所示[10]。

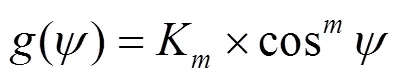
式中：入射角为雷电先导与垂直方向的夹角；、K为系数，在讨论冬季雷电时，=2，K=2/π，在讨论夏季雷电时，=3，K=3/4。由于多数雷击故障集中在夏季，因此本文采用=3。

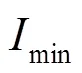
图2 平原和山区输电线路EGM模型示意图

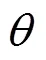
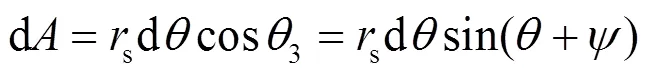
某一幅值和入射角度的雷电先导在垂直于先导入射方向的相应暴露面积为

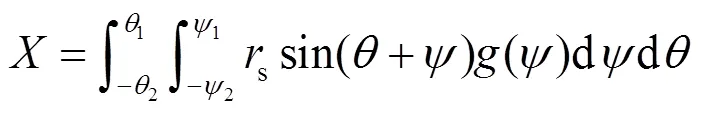
每年每单位长度线路绕击跳闸故障的次数为

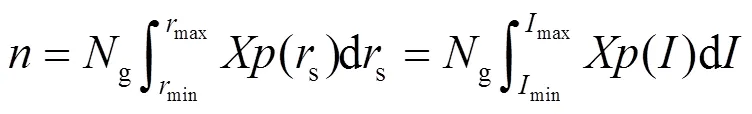
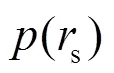
本文改进EGM模型的计算流程如图4所示。

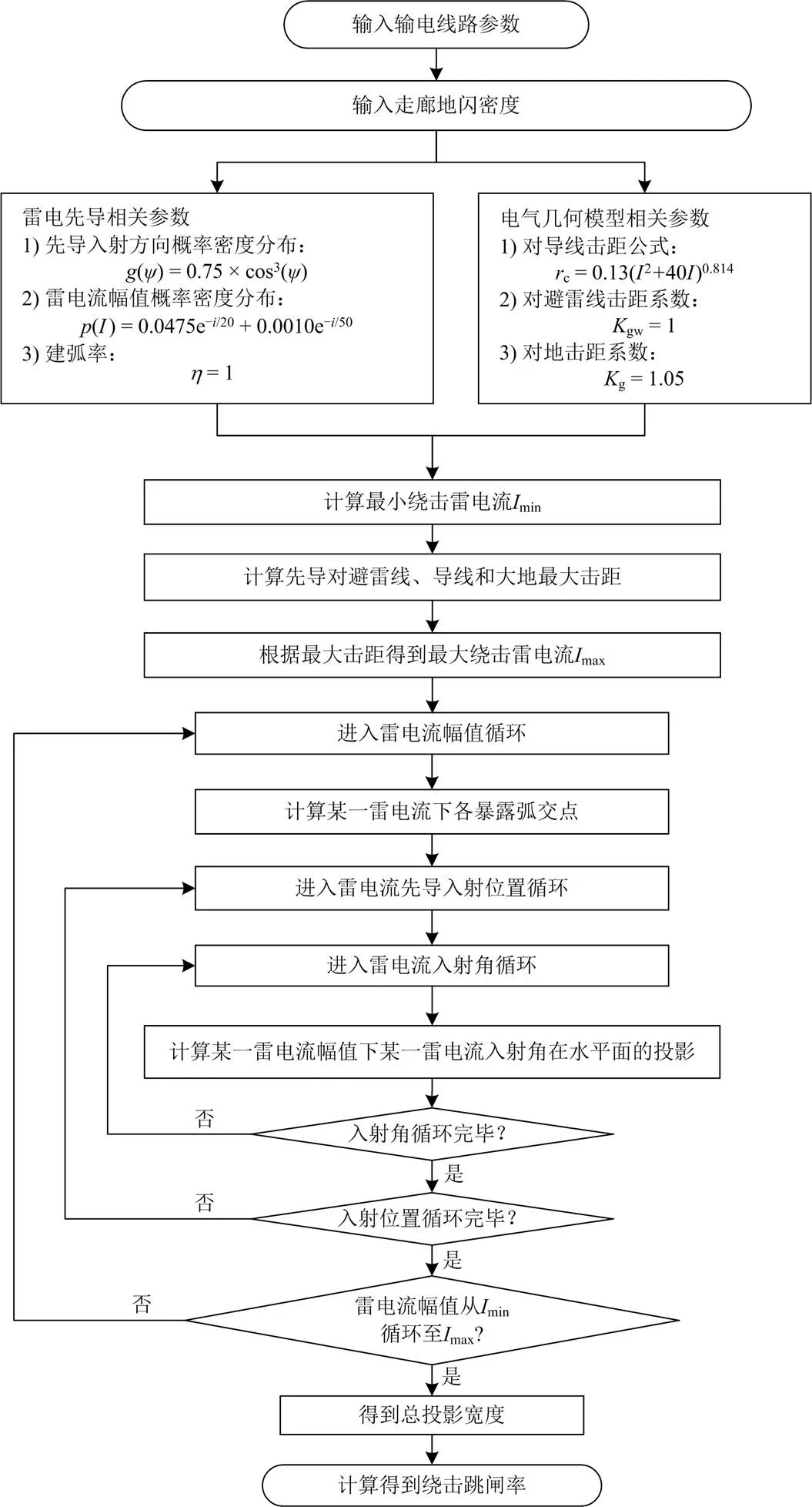
图4 改进EGM模型计算流程图

2 改进EGM模型的适用性验证与分析

2.1 与日本超特高压输电线路观测数据对比

为了验证本文改进EGM模型的适用性，采用本文改进EGM模型对日本500 kV、UHV输电线路的绕击概率进行计算，并将计算结果与经典EGM模型、文献[13]改进EGM模型以及日本长期雷击观测数据[25]进行对比。日本500 kV、UHV同塔双回输电线路具体参数如表1所示。

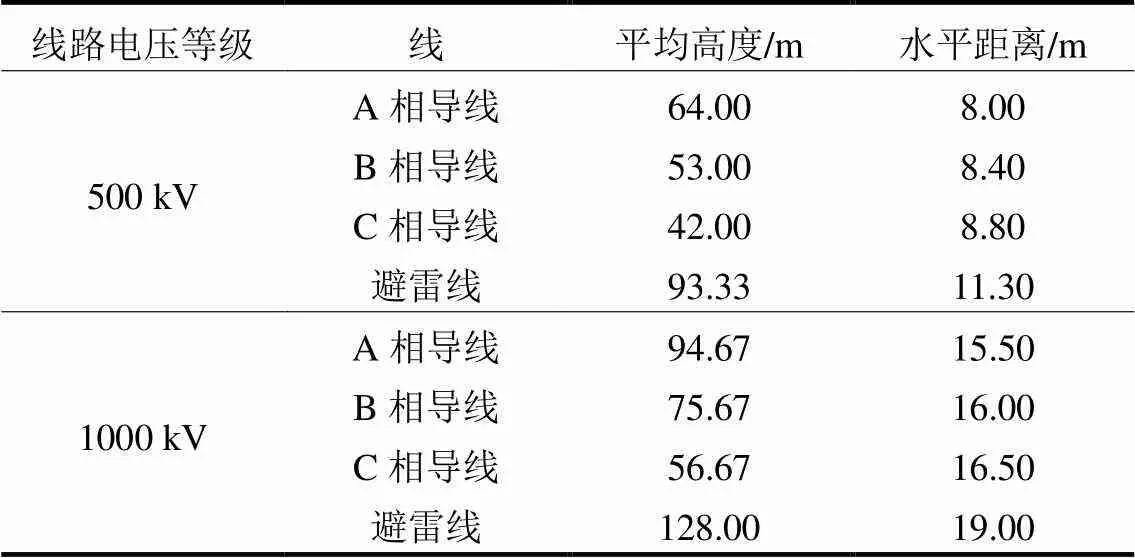
表1 日本同塔双回交流输电线路尺寸参数

对于地闪密度g，经典EGM模型中为3.0 次/ (km2·a)，日本500 kV线路途径地区为4.9 次/(km2·a)，UHV线路途径地区为5.2 次/(km2·a)[9]。

雷电流幅值概率密度为

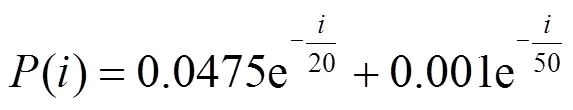
以日本对该线路的长期雷击观测数据[25]为参考，将本文改进EGM模型计算结果与采用经典EGM模型、文献[9]改进EGM模型和文献[13]改进EGM模型的计算结果进行对比，如图5、图6所示。

由图5、图6数据可以得到以下结论。

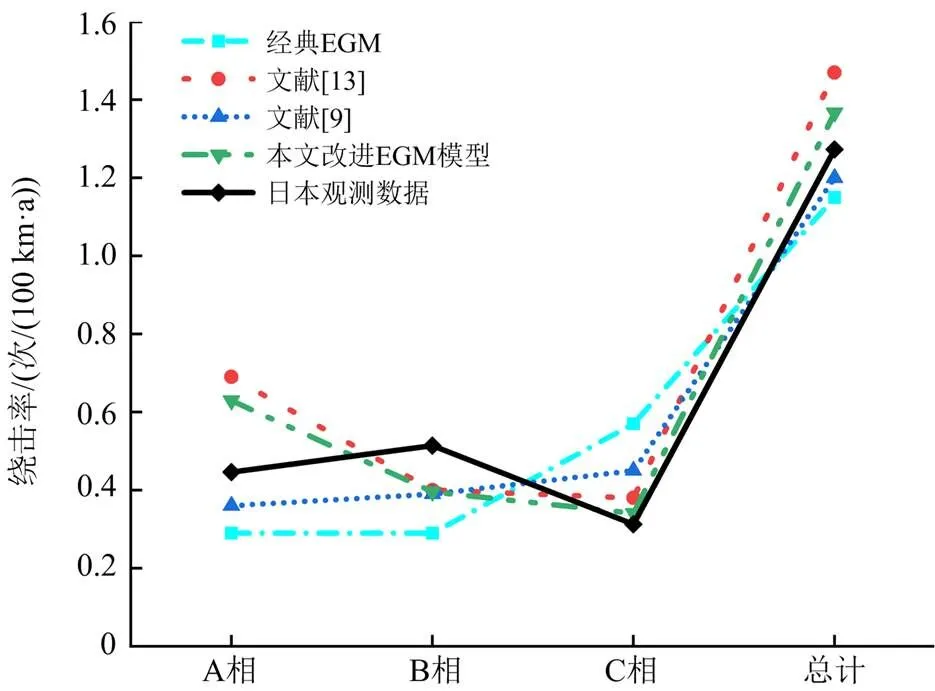
图5 日本500 kV输电线路绕击率对比图

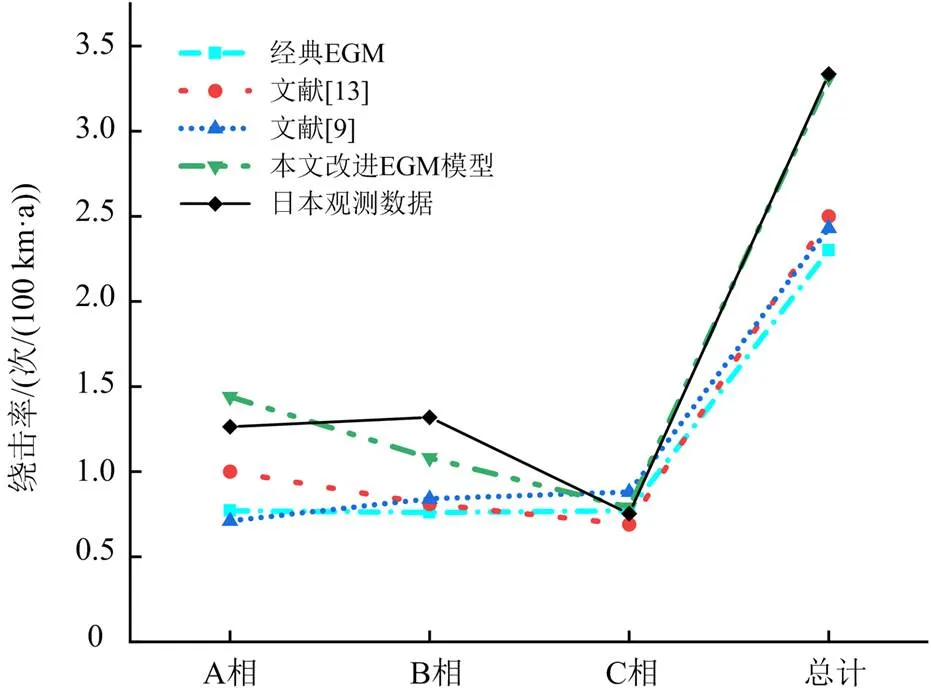
图6 日本UHV输电线路绕击率对比图

1) 图5中对于500 kV输电线路，本文改进EGM模型和文献[9]改进EGM模型的总绕击率与实际观测数据相差较小分别偏大7%和偏小6%，并且两个模型计算出的各相绕击率占比分别为45:30:25和30:32:38，相较于经典EGM模型和文献[13]改进EGM模型，与日本实际运行观测数据36:40:24更为接近。

2) 图6中对于UHV输电线路，本文改进EGM模型计算得到的绕击率更加接近日本实际观测数据，偏差仅-0.73%。并且计算得到的各相绕击率占比为43:33:24，相比于其他3种模型更接近日本实际运行观测数据的38:39:23。

2.2 与特高压输电线路雷电屏蔽模拟实验数据对比

为了进一步验证本文改进EGM模型的适用性，采用本文改进EGM模型对我国平原、山区特高压输电线路的雷电屏蔽性能进行计算，并与武汉大学、中国电力科学研究院针对特高压输电线路的雷电屏蔽性能模拟试验数据进行对比[11-14, 26-28]。其中，特高压杆塔型号为SZ322，山区地面倾角为30°，线路保护角为1.5°。文献[12-13]和文献[27-28]中高压棒电极头部距线路间隙距离为5 m，按照其缩比1:12.5可推算得到实际线路的击距为62.5 m。根据本文改进击距公式可推知，此时的雷电流幅值为28.7 kA。通过本文改进EGM模型计算该雷电流幅值下各相绕击暴露弧占总绕击暴露弧的比值，即可得到各相绕击占比。本文改进EGM模型计算得到的各相绕击占比与特高压输电线路雷电屏蔽试验的数据[12]对比，如图7所示。

图7中，本文改进EGM模型计算出的平原ABC三相绕击率占比为63%:37%:0，试验中ABC三相导线被击概率占比为52%:35%:12%，二者都表明绕击事故中A相占比最高，B相次之，C相最小。对于C相导线的绕击次数占比，本文改进EGM模型计算结果与试验结果存在一定偏差，考虑为C相导线位置相对较高，受放电方向分散性影响较大；在山区地形下，改进EGM模型计算出的ABC三相导线绕击次数占比为28%:38%:34%，与试验中ABC三相导线绕击次数占比25%:44%:31%有较好的一致性。

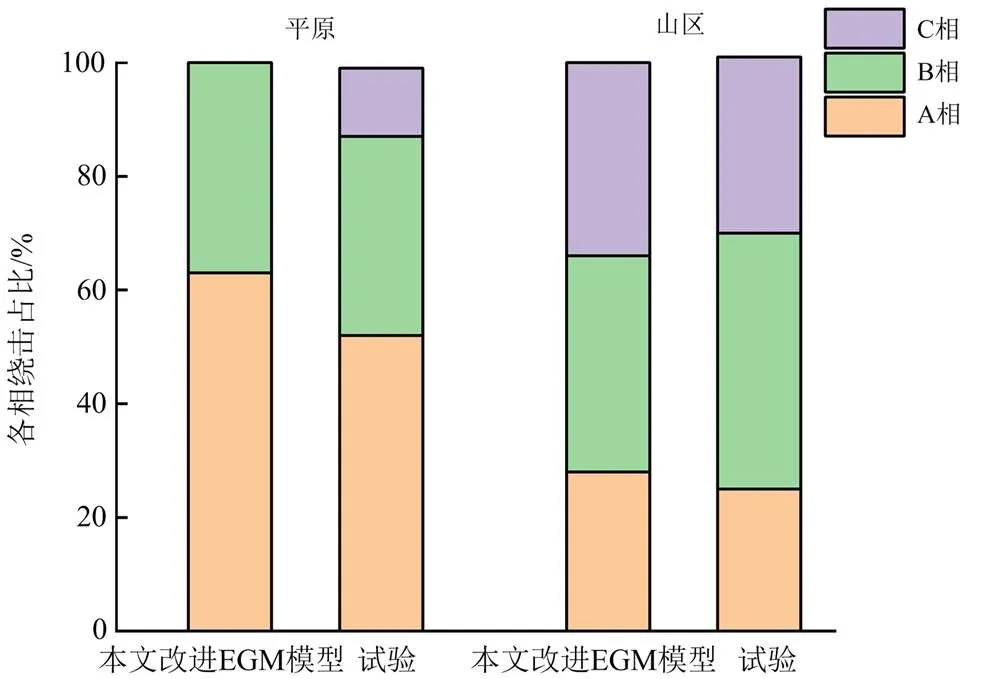
图7 各相导线绕击占比对比图

综上所述，采用本文改进EGM模型对大尺寸输电线路三相导线绕击率的计算结果与日本超、特高压输电线路雷电绕击观测数据及我国平原、山区特高压输电线路雷电屏蔽模拟试验的数据具有一致性，验证了本文改进EGM模型更适用于大尺寸特高压输电线路雷电屏蔽性能的计算。

3 不同地形下特高压输电线路雷电屏蔽性能分析

考虑到我国特高压输电线路途经地区地形复杂，且我国1000 kV输电线路所架设杆塔型式多样[29]，为了研究不同型式杆塔以及地形条件对我国1000 kV同塔双回输电线路绕击跳闸率的影响，本文选取SZ322型杆塔线路和SZT1型杆塔线路进行输电线路绕击跳闸率的计算，两型杆塔的结构图如图8所示，具体线路参数如表2所示。据文献[30]我国部分地区雷电地闪密度分布图可知，我国特高压交流线路所处地区地闪密度可取3次/(km2·a-1)。

将地形陡度设置为0°、5°、10°、15°、20°、25°、30°，分别计算不同地形陡度下不同杆塔型号特高压输电线路的绕击跳闸率，计算结果如图9所示。两种型号杆塔线路的绕击跳闸率都随着地形陡度的增大而增大，当地形陡度为0°(即平原)时，线路绕击跳闸率接近0，这与文献[14]改进EGM模型计算得到的SZT1型杆塔线路结果较为一致。而随着陡度的增大，线路绕击跳闸率也在增大且增大得越来越快，当陡度为30°时，SZT1型杆塔线路和SZ322型杆塔线路绕击跳闸率分别达到0.12 次/(100 km·a)和0.13 次/(100 km·a)。可见，相对于平原地区，我国特高压双回交流线路防雷击故障重心应聚焦到山区地形上，特别是地面倾角较大的地区。另外，在同一地形陡度下SZ322型杆塔线路的绕击跳闸率要高于SZT1型杆塔线路，可能是由于SZ322型杆塔高度明显高于SZT1型杆塔，从而SZ322型杆塔线路避雷线远高于SZT1型杆塔线路避雷线，而两者C相导线高度相差不大，导致SZ322型杆塔线路避雷线对导线的保护作用小于SZT1型杆塔线路，因而SZ322型杆塔线路遭受雷电绕击跳闸的概率相对SZT1型杆塔线路要高。整体来看，我国特高压同塔双回交流输电线路绕击跳闸率较低，但仍有发生跳闸故障的可能，这与我国特高压交流输电线路的实际运行现状较为吻合[31]。

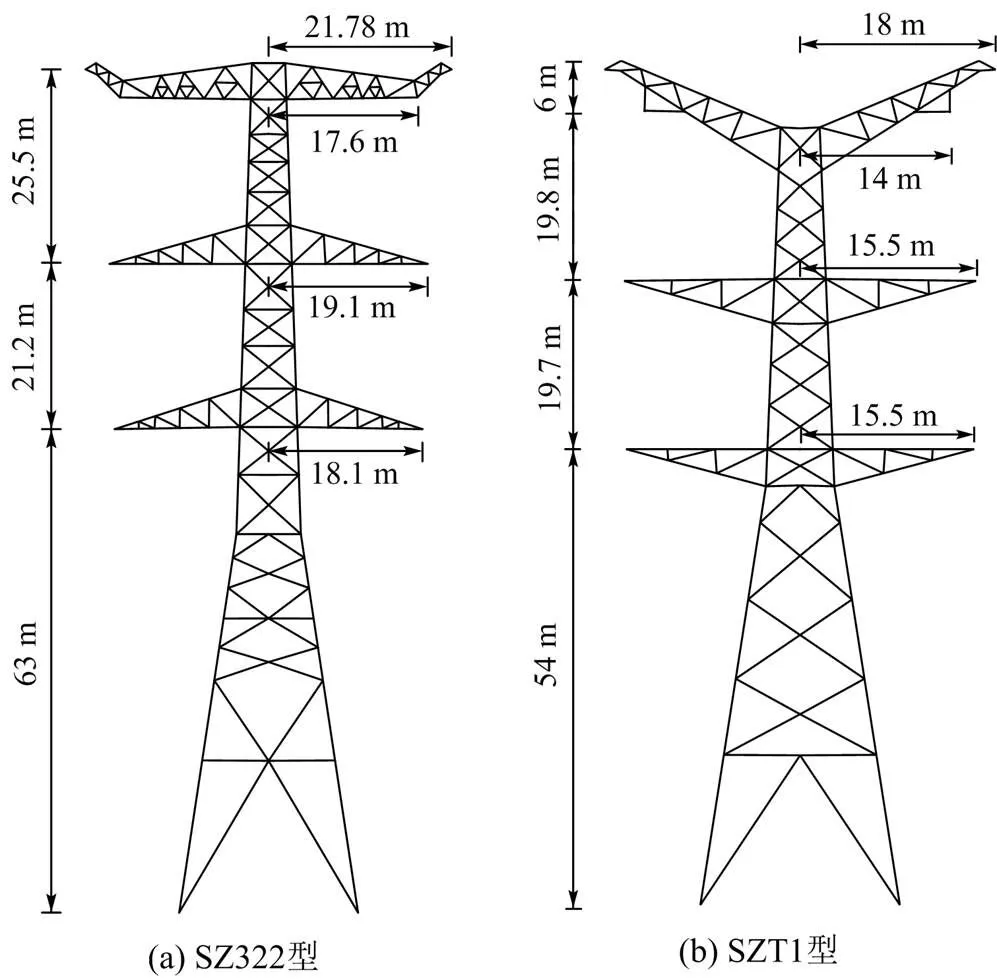
图8 SZT1型和SZ322型同塔双回杆塔结构图

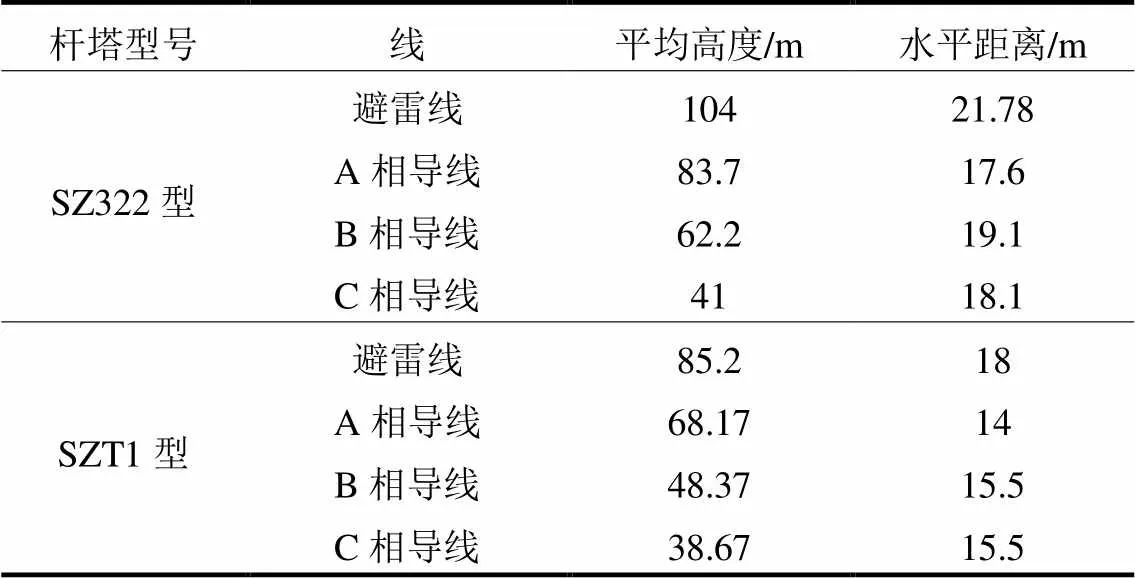
表2 SZT1型和SZ322型杆塔线路实际尺寸参数

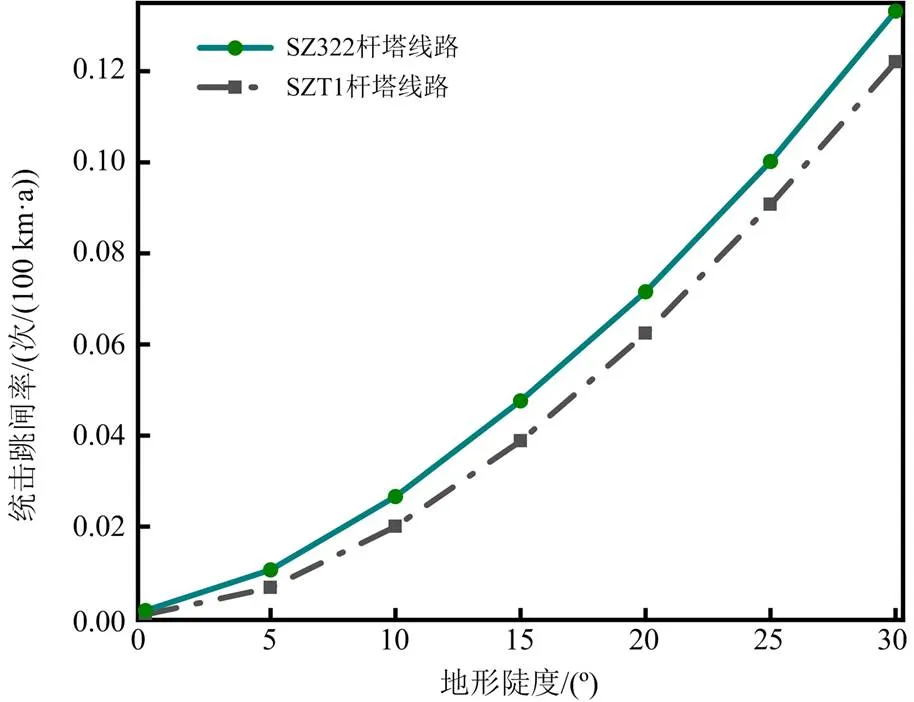
图9 不同杆塔型号下地形陡度对我国1000 kV线路绕击跳闸率的影响

4 结论

本文基于更符合特高压输电线路特点的长间隙放电试验数据和经学者验证过的雷电流回击速度公式，修正了现有击距公式，并利用改进EGM模型和特高压输电线路雷击模拟试验分析了地形对大尺寸输电线路雷击跳闸率的影响。

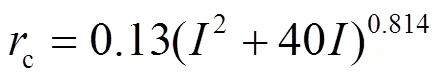
2) 改进EGM模型对日本超特高压输电线路的雷电绕击率计算结果更接近日本多年的雷电观测数据，且与我国特高压输电线路在平原和山区的雷击放电模拟试验结果具有一致性，验证了本文改进EGM模型在大尺寸输电线路中的适用性。

3) 杆塔构型、地形陡度对我国1000 kV线路绕击跳闸率具有显著影响。SZ322型杆塔特高压线路的绕击跳闸率高于SZT1型杆塔线路；随着地形陡度的增大，线路绕击跳闸率也在迅速增大。

[1] 吕哲, 王增平. 基于暂态波形特征的输电线路雷击干扰与故障识别方法[J]. 电力系统保护与控制, 2020, 48(6): 18-26.

LÜ Zhe, WANG Zengping. Identification of lightning strike disturbance and faults for transmission line based on transient waveform characteristics[J]. Power System Protection and Control, 2020, 48(6): 18-26.

[2] 邵庆祝, 赵晓东, 赵创业, 等. 基于高压直流输电线路分布参数模型的模态电流差动保护算法[J]. 电力系统保护与控制, 2021, 49(22): 171-179.

SHAO Qingzhu, ZHAO Xiaodong, ZHAO Chuangye, et al. Modal current differential protection method based on distributed parameter model of an HVDC transmission line[J]. Power System Protection and Control, 2021, 49(22): 171-179.

[3] 俞翔, 鲁江, 董云龙, 等. 适用于特高压多端混合直流输电系统的稳态电压控制方法[J]. 电力系统保护与控制, 2022, 50(1): 174-180.

YU Xiang, LU Jiang, DONG Yunlong, et al. A steady-state voltage control method for a multi-terminal hybrid UHVDC transmission system[J]. Power System Protection and Control, 2022, 50(1): 174-180.

[4] 徐友刚, 沈晓峰, 杨欢红, 等. 一种线路避雷器隐患查找用高压直流恒流源研制[J]. 电力系统保护与控制, 2021, 49(20): 160-166.

XU Yougang, SHEN Xiaofeng, YANG Huanhong, et al. Research and development of a high voltage DC constant current source for hidden fault detection of line arrester[J]. Power System Protection and Control, 2021, 49(20): 160-166.

[5] 席崇羽, 王海跃, 段非非, 等. ±800 kV特高压直流输电线路典型故障分析[J]. 湖南电力, 2016, 36(1): 55-59.

XI Chongyu, WANG Haiyue, DUAN Feifei, et al. Typical cases analysis of ±800 kV UHV DC transmission line[J]. Hunan Electric Power, 2016, 36(1): 55-59.

[6] 赵淳, 雷梦飞, 陈家宏, 等. 输电线路走廊雷电流幅值分布统计方法[J]. 高电压技术, 2017, 43(5): 1609-1614.

ZHAO Chun, LEI Mengfei, CHEN Jiahong, et al. Statistical method of lightning current amplitude distribution along transmission line corridor[J]. High Voltage Engineering, 2017, 43(5): 1609-1614.

[7] WAGNER C F, HILEMAN A R. The lightning stroke-II[J]. Power Apparatus and Systems, Part Ⅲ: Transactions of the American Institute of Electrical Engineers, 1961, 80(3): 622-636.

[8] ARMSTRONG H R, WHITEHEAD E R. Field and analytical studies of transmission line shielding[J]. IEEE Transactions on Power Apparatus and Systems, 1968, 87(1): 270-281.

[9] GRANT I S, ANDERSON J G , HILEMAN A R , et al. A simplified method for estimating lightning performance of transmission lines[J]. IEEE Transactions on Power Apparatus and Systems, 1985, PAS-104(4): 918-932.

[10] TANIGUCHI S, TSUBOI T, OKABE S, et al. Improved method of calculating lightning stroke rate to large-sized transmission lines based on electric geometry model[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2010, 17(1): 53-62.

[11] 王羽, 李志军, 戴敏, 等. 长空气间隙负极性操作冲击放电特性研究(I)—试验研究[J]. 中国电机工程学报, 2014, 34(21): 3534-3540.

WANG Yu, LI Zhijun, DAI Min, et al. Research on typical long air gaps with negative switching impulses(I)— experiments[J]. Proceedings of the CSEE, 2014, 34(21): 3534-3540.

[12] WANG Yu, WEN Xishan, LAN Lei, et al. Breakdown characteristics of long air gap with negative polarity switching impulse[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2014, 21(2): 603-611.

[13] 安韵竹. 基于长间隙负极性操作冲击放电的雷击特性研究[D]. 武汉: 武汉大学, 2015.

AN Yunzhu. Study on lightning stroke characteristics based on negative impulse discharge characteristics of long air gap[D]. Wuhan: Wuhan University, 2015.

[14] 王羽, 邓冶强, 文习山, 等. 基于长间隙放电试验适用于大尺寸输电线路的改进电气几何模型[J]. 中国电机工程学报, 2017, 37(12): 3654-3661.

WANG Yu, DENG Yeqiang, WEN Xishan, et al. An improved electric geometry model based on breakdown test of long air gaps and suited for large-sized transmission lines[J]. Proceedings of the CSEE, 2017, 37(12): 3654-3661.

[15] IDONE V P, ORVILLE R E, HUBERT P, et al. Correlated observations of three triggered lightning flashes[J]. Journal of Geophysical Research Atmospheres, 1984, 89(D1): 1385-1394.

[16] LUNDHOLM R. Calculation of transmission line lightning voltages by field concepts[J]. Transactions of the American Institute of Electrical Engineers Part III Power Apparatus & Systems, 1957, 76(3): 1271-1281.

[17] 蒋圣超, 朱时阳, 陈曦, 等. 真实起伏地形对雷电电磁场传播的模拟研究[J]. 电气技术, 2020, 21(8): 33-39.

JIANG Shengchao, ZHU Shiyang, CHEN Xi, et al. Study on the influence of real undulating terrain on lightning electromagnetic propagation[J]. Electrical Engineering, 2020, 21(8): 33-39.

[18] 欧阳仁乐. 1000 kV杆塔防雷研究[J]. 电气技术, 2014(11): 13-17.

OUYANG Renle. Research of lightning protection of 1000 kV tower[J]. Electrical Engineering, 2014(11): 13-17.

[19] 姚陈果, 王婷婷, 杨庆, 等. 特高压交流输电线路绕击耐雷性能仿真分析[J]. 高电压技术, 2013, 39(3): 526-533.

YAO Chenguo, WANG Tingting, YANG Qing, et al. Simulated analysis of lightning shielding failure performance of UHVAC transmission lines[J]. High Voltage Engineering, 2013, 39(3): 526-533.

[20] WAGNER F C. The relation between stroke current and the velocity or the return stroke[J]. IEEE Transactions on Power Apparatus Systems, 1963, 82(68): 609-617.

[21] ARMSTRONG H R, WHITEHEAD E R. Field and analytical studies of transmission line shielding[J]. IEEE Transactions on Power Apparatus and Systems, 1968, 87(1): 270-281.

[22] ANDERSON J G, CLAYTON R, ELAHI H, et al. Estimating lightning performance of transmission lines II updates to analytical models[J]. IEEE Transactions on Power Delivery, 1993, 8(3): 1254-1267.

[23] GOLDE R H. Lightning (Vol. 1)[M]. London: Academic Press, 1977.

[24] 司马文霞, 杨庆, 李永福, 等. 输电线路雷电绕击评估方法分析及展望[J]. 高电压技术, 2015, 41(8): 2500-2513.

SIMA Wenxia, YANG Qing, LI Yongfu, et al. Analysis and prospect of lightning shielding failure evaluation methods of transmission lines[J]. High Voltage Engineering, 2015, 41(8): 2500-2513.

[25] TANIGUCHI S, TSUBOI T, OKABE S. Observation results of lightning shielding for large-scale transmission lines[J]. IEEE Transactions on Dielectrics & Electrical Insulation, 2009, 16(2): 552-559.

[26] 彭谦, 李军, 卞鹏, 等. 改进电气几何模型法在1000 kV输电线路雷电绕击跳闸率计算中的应用[J]. 电网技术, 2010, 34(9): 155-159.

PENG Qian, LI Jun, BIAN Peng, et al. Application of improved electrical geometry model method in calculation of lightning tripping rate of 1000 kV transmission line[J]. Power System Technology, 2010, 34(9): 155-159.

[27] 王羽. 长间隙放电特性试验研究及在防雷中的应用[D]. 武汉: 武汉大学, 2012.

WANG Yu. Experimental study of breakdown characteristics of long air gaps and their applications in lightning protection[D]. Wuhan: Wuhan University, 2012.

[28] 刘宗喜, 蓝磊, 王羽, 等. 地形对特高压同塔双回输电线路雷电屏蔽性能的影响[J]. 高电压技术, 2016, 42(9): 2950-2955.

LIU Zongxi, LAN Lei, WANG Yu, et al. Effect of terrains on lightning shielding performance of UHV common-tower double-transmission lines[J]. High Voltage Engineering, 2016, 42(9): 2950-2955.

[29] ZHANG Baohui, HAO Zhiguo, BO Zhiqian. New development in relay protection for smart grid[J]. Protection and Control of Modern Power Systems, 2016, 1(2): 121-127.

[30] 谷山强, 王剑, 冯万兴, 等. 电网雷电监测数据统计与挖掘分析[J]. 高电压技术, 2016, 42(11): 3383-3391.

GU Shanqiang, WANG Jian, FENG Wanxing, et al. Statistical and mining analysis of lightning detection data in power grid[J]. High Voltage Engineering, 2016, 42(11): 3383-3391.

[31] 王剑, 谷山强, 彭波, 等. 国网辖区特高压直流线路防雷运行现状分析[J]. 全球能源互联网, 2018, 1(4): 511-520.

WANG Jian, GU Shanqiang, PENG Bo, et al. Research on lightning protection operation status of UHVDC transmission lines in SGCC[J]. Journal of Global Energy Interconnection, 2018, 1(4): 511-520.

Applicability and verification of an improved EGM model for UHV transmission lines

YANG Minghao1, AN Yunzhu1, HU Yuanchao1, LI Zhijun2, FENG Shouxin1

(1. School of Electrical and Electronic Engineering, Shandong University of Technology, Zibo 255000, China;2.China Electric Power Research Institute, Wuhan 430074, China)

To analyze the lightning shielding performance of UHV transmission lines in China more accurately, based on the long air gap discharge test data and lightning return stroke observation data in China, an improved EGM model suitable for lightning shielding performance evaluation of large-scale transmission lines considering terrain conditions is established and verified. The strike distance formula is modified tos= 0.13(2+ 40)0.814. The calculation results of lightning shielding failure rate of three-phase conductors of EHV and UHV transmission lines by the improved EGM model are consistent with the lightning observation data of actual lines in Japan and the lightning simulation test data of UHV transmission lines in plains and mountains of China. This verifies the applicability of the improved EGM model. The improved EGM model is used to evaluate the influence of tower type and slope steepness on shielding failure trip rate of UHV transmission lines. The results show that the shielding failure trip rate of SZ322 tower is higher than that of SZT1 tower, and the shielding failure trip rate of a UHV line increases with the increase of slope steepness. The correction of the EGM model and the optimization of calculation method in this paper have a certain guiding significance for the design of lightning shielding performance of UHV transmission lines in China.

UHV transmission line; simulation test of lightning shielding; electric geometry model (EGM); striking distance formula

10.19783/j.cnki.pspc.220353

国家自然科学基金项目资助(51807113)

This work is supported by the National Natural Science Foundation of China (No. 51807113).

2022-03-17；

2022-05-31

杨明浩(1997—)，男，硕士，研究方向为电力系统防雷与过电压防护；E-mail: yangminghaosdut@163.com

安韵竹(1988—)，女，博士，副教授，研究方向为电力系统防雷与接地、过电压保护；E-mail: anyunzhu2006@ 163.com

胡元潮(1988—)，男，通信作者，博士，副教授，研究方向为输电线路防雷与接地技术，电工材料及其应用技术。E-mail: huyuanchao3211@126.com

(编辑 许 威)