模块化多电平变换器分数阶PIl 环流抑制策略

郑 征，李佩柯，李绍令，王肖帅，靳婷婷

模块化多电平变换器分数阶PI环流抑制策略

郑 征，李佩柯，李绍令，王肖帅，靳婷婷

(河南理工大学电气工程与自动化学院，河南 焦作 454000)

模块化多电平变换器(modular multilevel converter, MMC)内部环流增加系统功率损耗，加剧桥臂电流畸变。针对传统PI环流控制器存在鲁棒性较差、控制精度有限等问题，将分数阶PI控制器应用于MMC环流抑制。首先，对MMC工作特性进行分析，阐述环流产生机理。其次，研究分数阶PI控制结构，并设计MMC分数阶PI环流抑制策略。然后，采用经典频域法优化分数阶PI控制器参数，并对分别采用传统PI和分数阶PI控制器的系统环流控制性能进行对比分析。最后，在相同条件下，通过对采用上述两种环流抑制策略的MMC系统，分别在电源扰动、直流侧电压阶跃和三相不平衡工况下进行仿真研究。结果表明，分数阶PI环流抑制器的抗电源扰动性和环流抑制能力均优于传统PI环流抑制器，更适用于MMC此类的非线性系统的控制。

模块化多电平变换器；环流抑制；分数阶FO-PI

0 引言

模块化多电平变换器(modular multilevel converter, MMC)采用多个相同子模块级联的工作结构，一方面，模块化的设计可以方便地通过安装冗余来提高变换器工作可靠性；另一方面，可提高变换器工作电压等级[1-5]。目前，MMC型HVDC已成为高压直流输电的主要方式[6-9]。然而，在功率传输过程中，不断地对子模块电容进行充放电会造成子模块电容电压失衡和相间环流等问题[10-14]，本文主要针对环流问题进行研究。

为满足对环流精确快速抑制，许多先进的控制算法应用于环流抑制[15-19]。文献[20]采用无源控制方法，只能在一定程度上减小环流幅值但不会完全消除，且会增加系统体积、成本与损耗。文献[21-22]采用传统整数阶PI(IO−PI)控制器，通过坐标变换将三相环流分解为坐标系下的直流分量进行抑制。虽然IO−PI控制器具有结构简单、操作方便的优点，但其控制参数受外部影响较大，系统鲁棒性较差，控制精度有限，并不适合MMC此类非线性系统[23]。

为提高控制器控制性能，许多研究者将分数阶理论引入控制系统，通过采用分数阶控制器达到提高系统性能的目的[24]。分数阶PID控制器相较于传统PID控制器，增加了两个自由度变量和[25]，且和取值为实数，使得控制器调节范围更加灵活；但在实际应用中由于参数设计复杂性大大提高，往往摒弃微分环节，使用分数阶PI(FO-PI )控制器。文献[26]将整数阶PI控制器分数阶PI 控制器分别应用于永磁同步电动机的速度控制系统，通过对比分析，采用分数阶PI 控制器的系统在响应速度和跟随性能上均优于采用整数阶PI控制器的系统。文献[27]使用分数阶PI 控制器对APF直流侧电压进行控制，在负载扰动和电压闪变情况下，分数阶PI 控制器均能快速精确地将直流侧电压稳定在给定值，在两种情况下性能均优于整数阶PI控制器。

本文以模块化多电平变换器的环流问题作为研究对象，设计基于分数阶PI 环流抑制策略，并给出最优参数设计方法。在3种不同工况下进行仿真分析，并与按照最优参数设计的传统PI环流抑制器进行对比，验证了分数阶PI环流抑制策略的可行性。

1 MMC内部环流产生机理

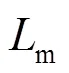
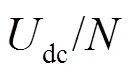
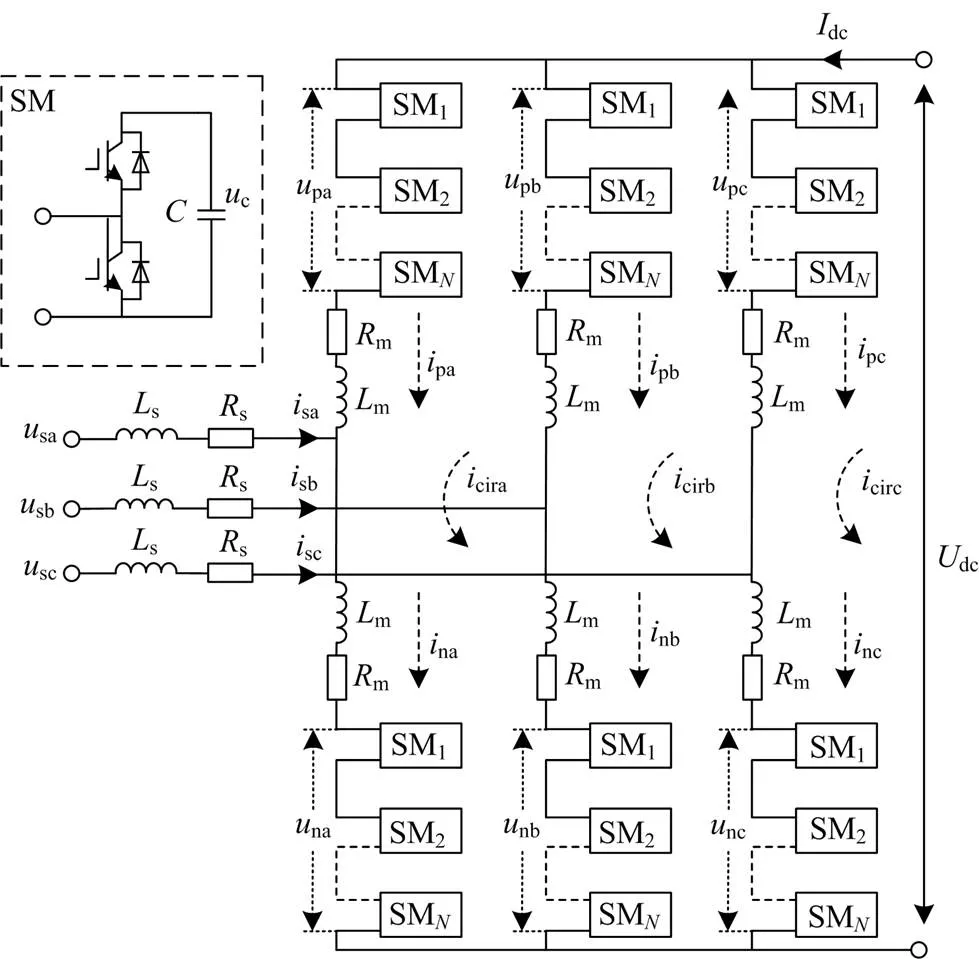
图1 MMC拓扑结构

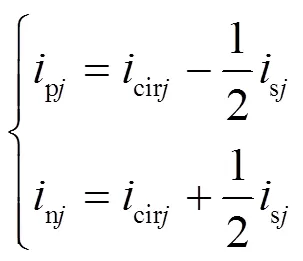
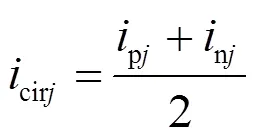
对上、下桥臂分别列写KVL方程，并结合图2中MMC单相等效电路进行推导，可得单相MMC数学模型为

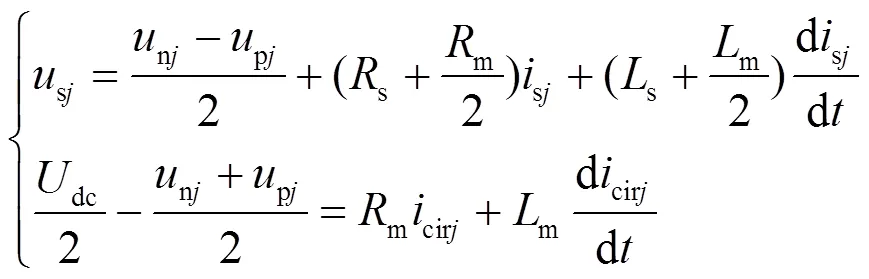
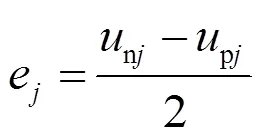
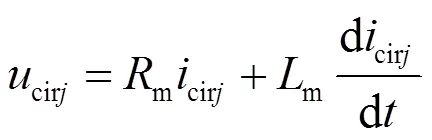
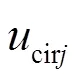
2 基于FO-PIl 的MMC环流抑制策略

MMC环流的特点是强耦合、非线性，传统IO-PI环流控制器虽然结构简单，但其控制性能对系统参数比较敏感，抗干扰性能较差，调节过程灵活性不够[21-22]。基于以上问题，为了得到更好的环流抑制效果，并提高系统鲁棒性，本文引入分数阶PI环流抑制器对环流中二倍频负序分量进行抑制。

2.1 MMC分数阶PIλ控制结构

由式(6)可得，三相之间二倍频环流呈现负序特征，首先通过坐标变换将三相静止坐标系下的二倍频负序分量转换为旋转坐标系下轴上的直流量，变换矩阵为

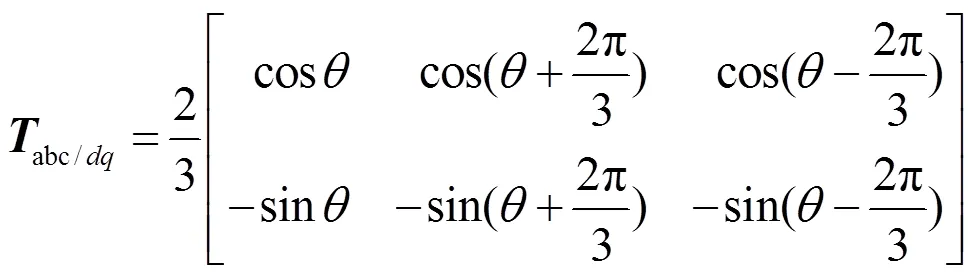
经过二倍频负序旋转坐标变换，结合式(5)可以得到MMC三相环流在旋转坐标系下的电压方程为

根据式(8)设计了基于FO-PI环流抑制的控制框图，如图3所示。

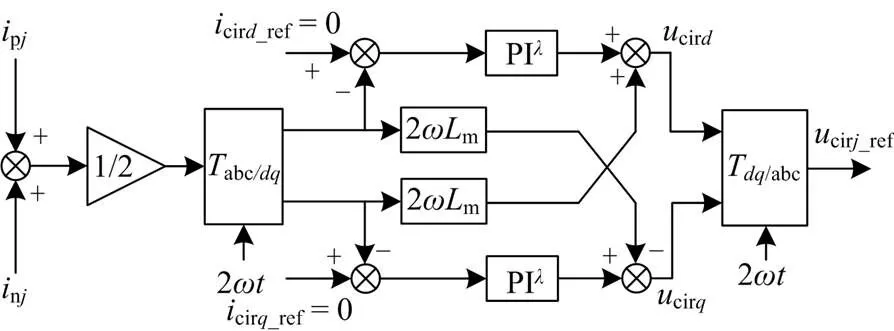
图3 基于FO-PIl环流抑制器控制框图

通过FO-PI环流抑制器与轴解耦可得到不平衡压降在旋转坐标系下的参考值，经过/abc坐标反变换后，将三相静止坐标系下的不平衡压降cirj_ref叠加至各相上、下桥臂电压参考信号中。其中，分数阶控制器的合理性与科学性[25]已在实践中证实，其控制器结构框图如图4所示。

图4 FO-PIl控制器结构框图

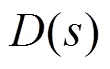
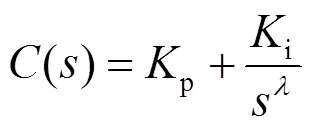
相比于传统IO-PI控制器增加了可调参数，即积分阶次，通过调节积分阶次，可以灵活改变伯德图幅频曲线斜率和相频特性相角，使得幅频曲线斜率在0～20 dB/dec之间变化，相频曲线相角在0～90°之间变化。因此，分数阶控制器调节空间更加广阔，针对不同系统可以更加精确地对控制器进行调节，提高了系统自适应能力。

2.2 分数阶PIl控制器参数设计

根据式(9)将FO-PI控制器传递函数改写为

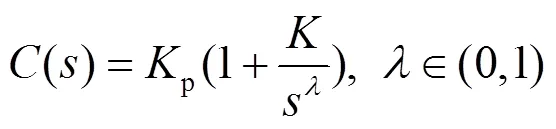
本文在考虑桥臂电流采样的延迟环节和PWM控制的小惯性特性的基础上，采用文献[27]提出的Flatphase与经典的相位裕度和幅值裕度相结合的方法，对分数阶环流控制器参数进行优化设计。

1) 幅值条件

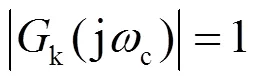
2) 相位裕度

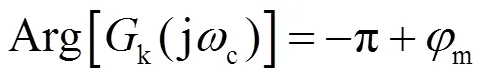
3) 系统鲁棒性

2为简化系统设计，将延迟环节与小惯性环节进行合并，解耦后简化的d轴传递函数模型如图5所示。

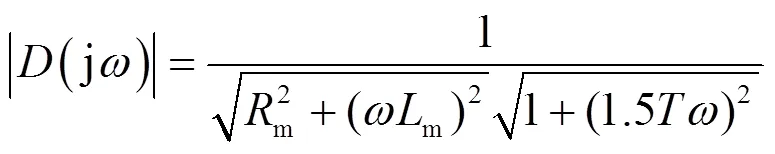
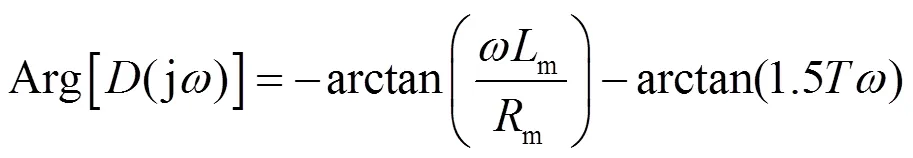
FO-PI控制器的幅值和相位可写为

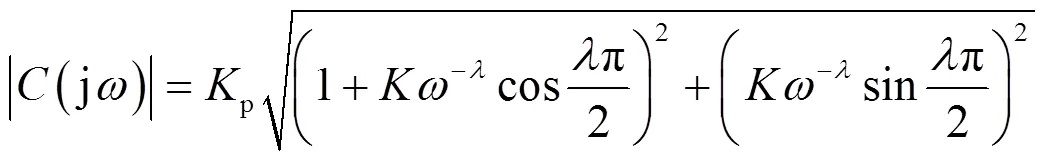
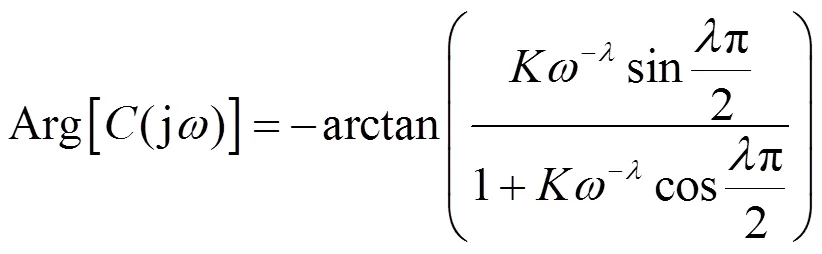
为满足相角裕度条件，联立式(12)、式(15)和式(17)可求得与之间的关系式为

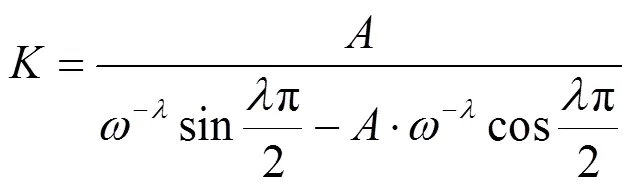
为满足系统鲁棒性要求，联立式(13)、式(15)和式(17)进行推导可以得到

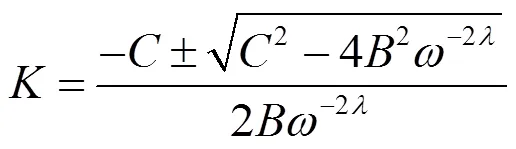
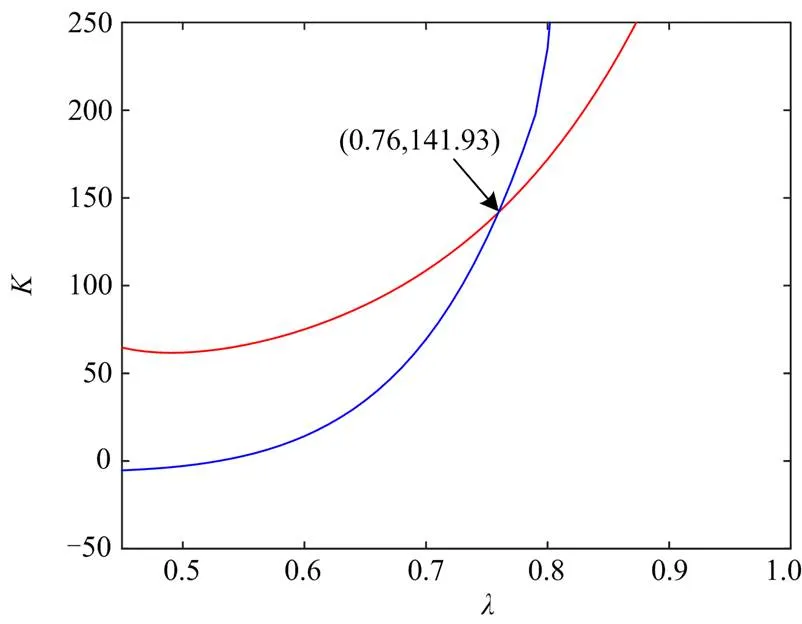
图6 K与λ关系曲线

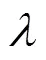
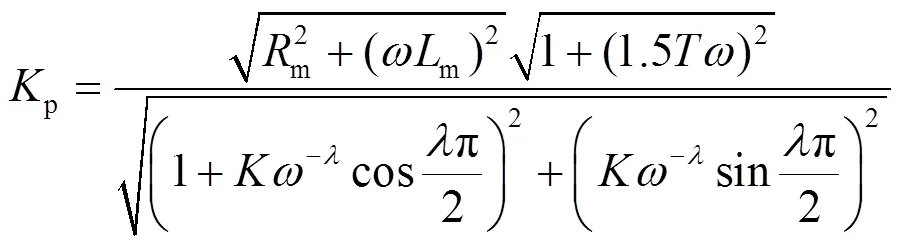
2.3 MMC环流控制性能分析

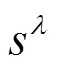
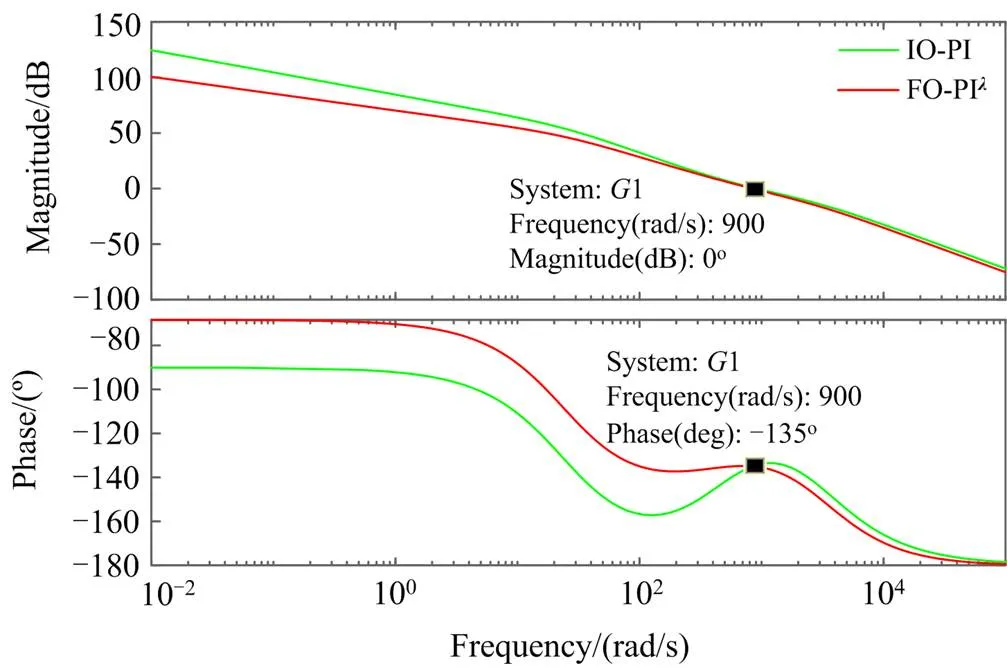
图7 采用IO-PI和FO-PIl控制器的系统开环伯德图

由图7可以看出，对比低频段特性，FO-PI控制器相对于IO-PI控制器可以使系统有着更强的稳定性；而且在截止频率处FO-PI控制器下系统的相位变化相对平缓，使得系统有着更强的鲁棒性；在高频段处，FO-PI控制器下系统的幅频特性曲线在IO-PI控制器曲线的下方，使得系统有着更强的抗干扰能力。

通过系统伯德图综合对比分析两种控制器下系统的各频段特性，FO-PI控制器可针对不同系统进行更精确的调节，更适用于MMC此类非线性耦合系统。

3 仿真分析

为验证本文环流抑制策略的有效性，并对比FO-PI环流抑制器与IO-PI环流抑制器的优劣性，本文基于Matlab/Simulink环境搭建了三相五电平的MMC整流仿真模型，分别对两种环流抑制器在电源侧扰动、直流侧电压阶跃和三相不平衡3种工况下进行对比仿真研究。FO-PI控制器参数为2.2节计算所得的最优参数，具体仿真参数如表1所示。

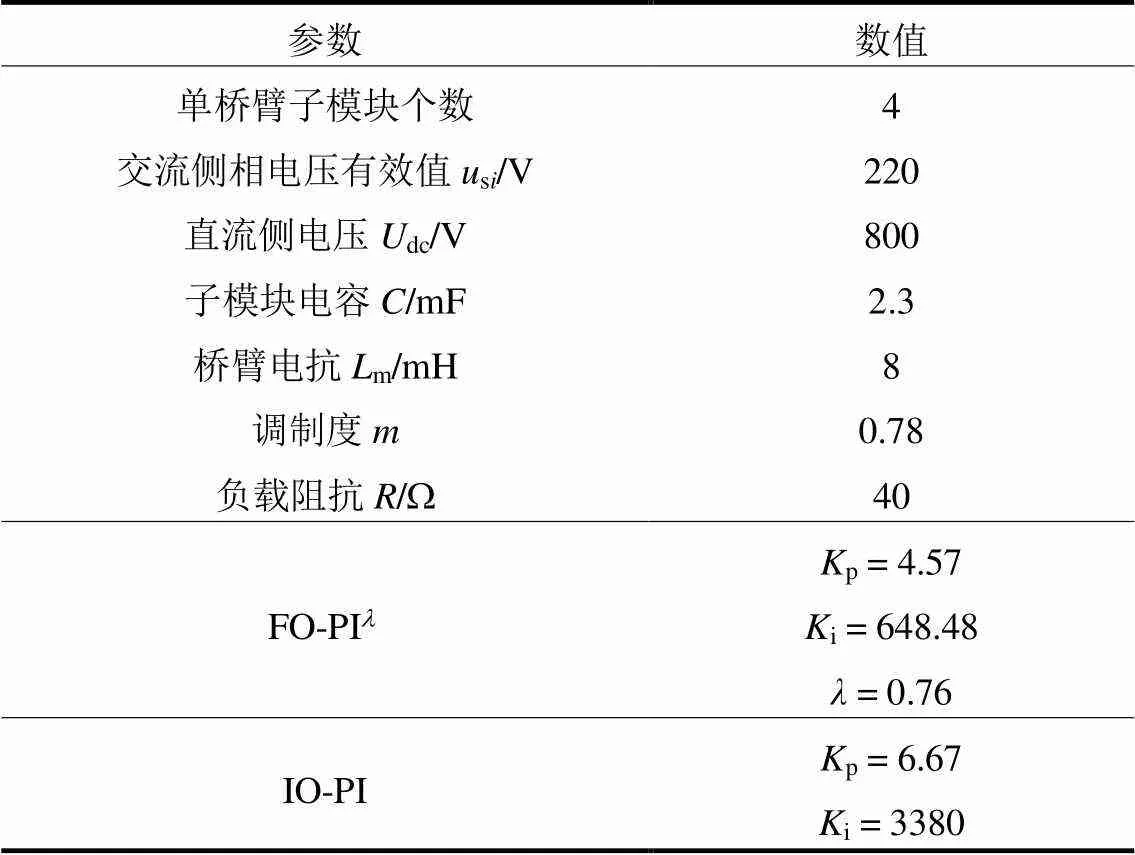
表1 MMC系统仿真参数

3.1 环流控制器抗扰动性能仿真分析

在上述仿真参数下，以A相为例进行分析，在0.15 s时分别投入IO-PI和FO-PI两种环流抑制器进行稳态对比仿真；在0.3 s时加入交流侧幅值升高5%的扰动，一个工作周期后于0.32 s恢复正常，以验证系统抗电源扰动性能。交流侧扰动工况下A相环流波形如图8所示。

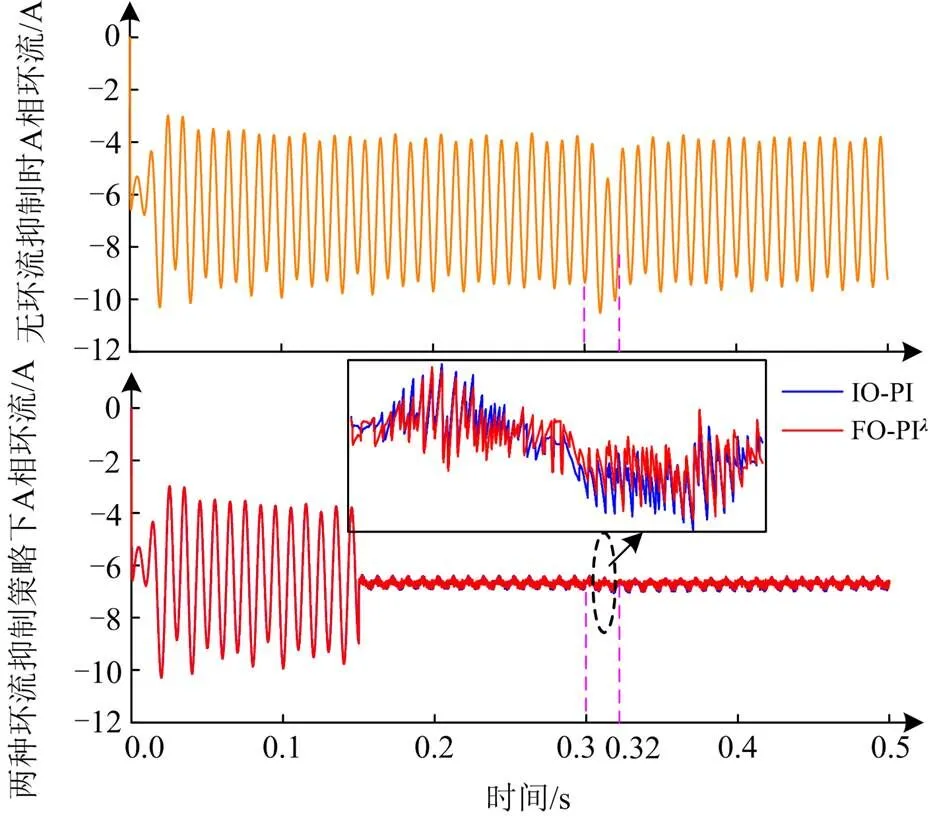
图8 交流侧扰动工况下A相环流波形

由图8可知，在0.3～0.32 s扰动期间，两种环流抑制器均能将环流控制在一定范围内，相比之下，FO-PI环流抑制器控制下环流波动程度明显小于IO-PI环流抑制器。为了对两种环流抑制器抗扰动性能进行详细对比分析，分别在扰动前后对环流进行5个周期的FFT分析，各分量占比以直流分量为基值，具体数据如表2所示。

表2 交流侧扰动工况下A相环流FFT分析

将表2中数据绘制为柱状图，如图9所示，可直观看出，在扰动前后两种稳态情况下，使用FO-PI环流抑制器下总谐波占比和二倍频环流占比控制效果都优于IO-PI 环流抑制器。通过对同一环流抑制器扰动加入前后的总谐波占比与二倍频分量占比分析可知，FO-PI环流抑制器控制下扰动加入前和扰动切除后总谐波占比与二倍频分量占比变化更小，系统抗干扰性更好。

图9 交流侧扰动工况下A相环流FFT分析

综合分析，本文以扰动加入前后环流总谐波占比的变化量作为变换器抗干扰能力敏感性评价指标，分别在扰动为5%、10%、15%和20%情况下进行仿真，得到两种环流抑制器下总谐波占比变化量如图10所示。

由图10可直观看出，随着扰动幅度的增大，IO-PI环流抑制器下扰动前后环流总谐波占比变化量显著增加，环流抑制器抗干扰能力敏感性迅速增加；而FO-PI环流抑制器下扰动前后总谐波占比变化量较小，抗干扰较强，且当扰动幅度增大到15%后FO-PI环流抑制器抗干扰能力敏感性不再增加。由此可验证，FO-PI环流抑制器稳态性能和抗干扰性能均优于FO-PI环流抑制器。

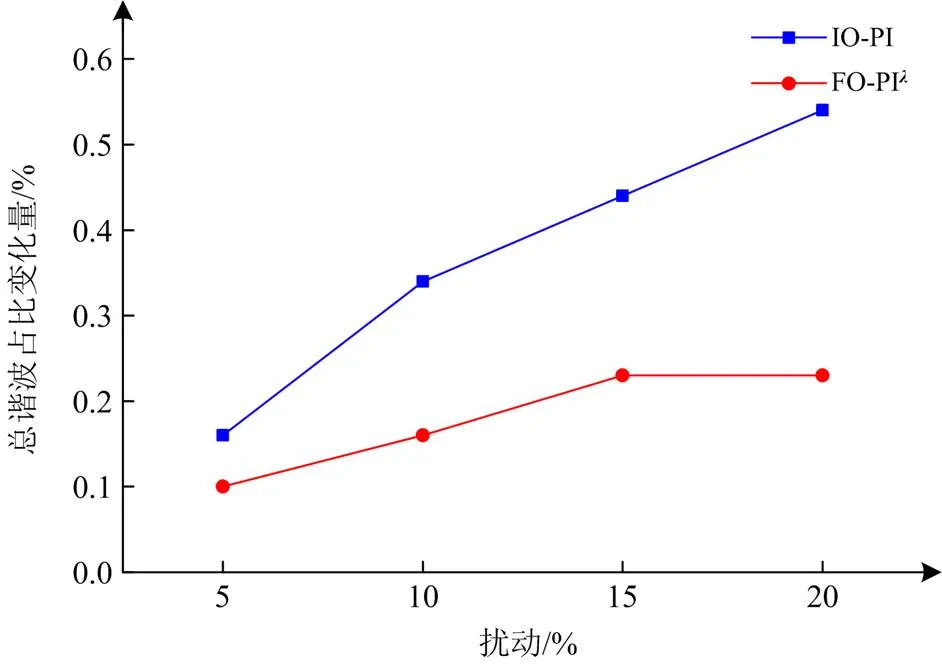
图10 环流抑制器抗干扰能力敏感性分析

3.2 直流侧电压阶跃时环流抑制效果对比

变换器工作于闭环整流状态，在0.15 s时分别投入IO-PI和FO-PI两种环流抑制器，在特殊性负载要求下，运行至0.2 s时将直流侧输出电压由800 V提高至960 V，以模拟在直流侧电压阶跃工况下不同环流抑制器的环流抑制能力。

图11为直流电压阶跃情况下A相环流波形，0～0.2 s时直流输出电压为800 V，0.2 s时直流输出电压阶跃至960 V。由图11可知，对比无环流抑制下A相环流波形，两种环流抑制策略在动态情况下均可有效降低环流波动幅值，至0.22 s可达到新的稳定状态。为了更清晰地对比分析两环流抑制器在电压阶跃动态过程中的环流抑制情况，在0.2～ 0.22 s处对系统A相环流进行FFT分析，具体数据如表3所示。

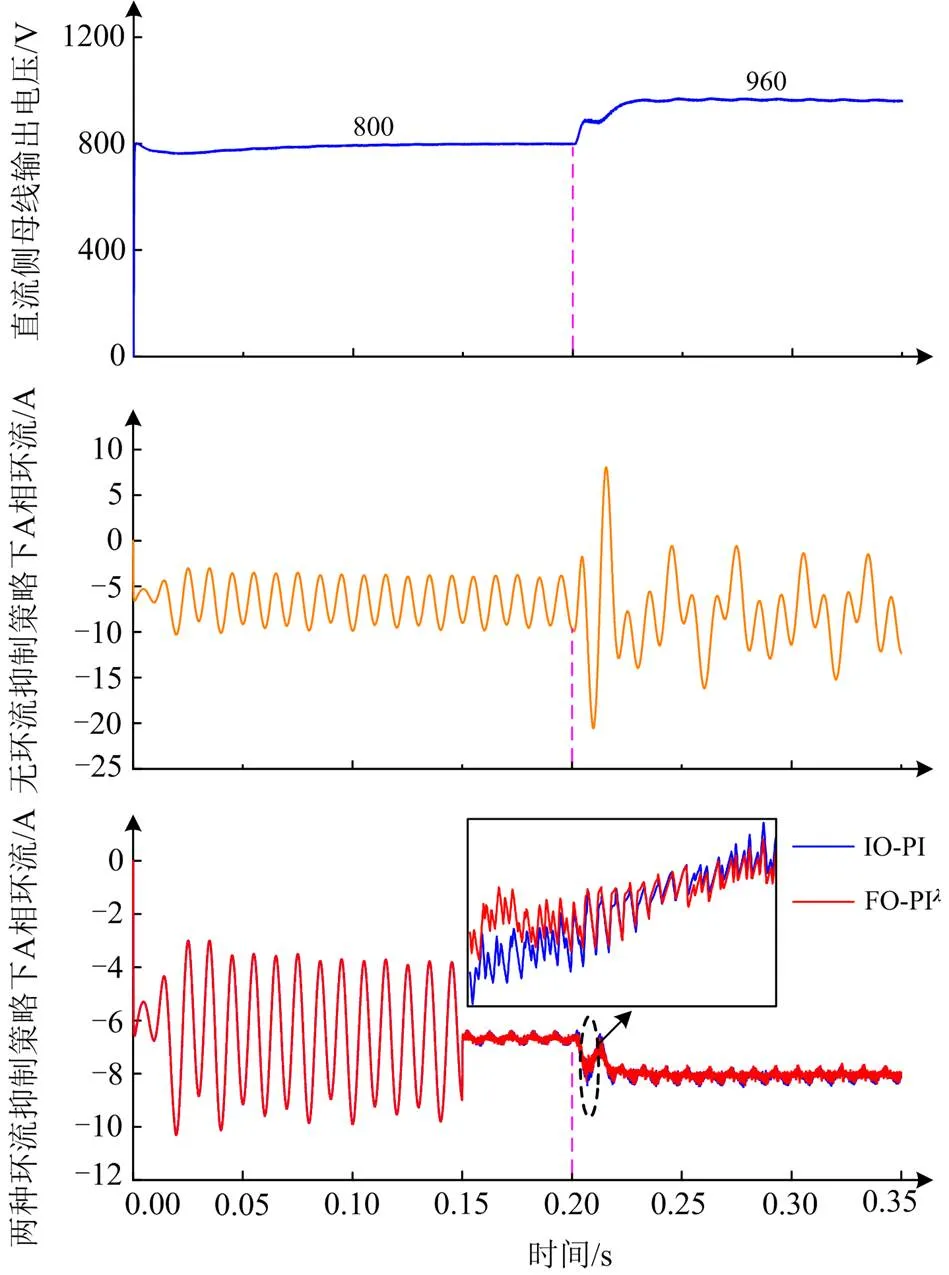
图11 直流电压阶跃情况下A相环流波形

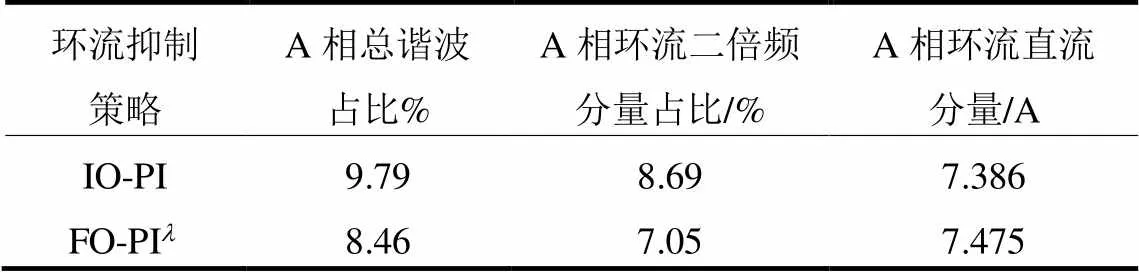
表3 直流电压阶跃时A相环流FFT分析

分析表3中数据可知，FO-PI环流抑制器的A相环流总谐波占比较IO-PI环流抑制器下降1.33%，环流二倍频分量占比下降1.64%。因此，在环流总谐波和二倍频分量抑制上，FO-PI环流抑制器控制效果均优于IO-PI环流抑制器。经上述对比分析，在直流电压阶跃工况下，FO-PI环流抑制器相较于IO-PI环流抑制器有着更好的动态性能。

3.3 交流侧电压不平衡时环流抑制效果对比

在表1仿真参数的条件下，将B相电压幅值下降20%，在0.15 s时，分别投入IO-PI和FO-PI两种环流抑制器，以模拟在三相电压不平衡工况下不同环流抑制器的性能。

图12为三相不平衡工况下三相环流波形。在两种环流抑制策略下A、C两相环流都可得到快速有效抑制，对比B相环流波动程度，系统环流抑制能力由强到弱为FO-PI＞IO-PI＞无环流抑制。为详细分析，在0.15 s时开始对B相环流进行10个周期的FFT分析，具体数据如表4所示。

分析表4中数据可知，FO-PI环流抑制器的B相环流总谐波占比较IO-PI环流抑制器下降0.76%，环流二倍频分量占比下降0.79%。而且通过对A相和C相仿真数据进行分析可知，在此不平衡情况下，FO-PI环流抑制器控制下A相和C相的总谐波占比与二倍频分量占比增加量均小于IO-PI环流抑制器控制下的增加量。

由仿真参数可知，在理想情况下，各相环流中直流分量应为6.6 A，而对比B相两种环流抑制器下的直流分量值可知，FO-PI环流抑制器控制下直流分量更接近理想值。

因此，经上述对比可知，在三相不平衡工况下，FO-PI抑制器性能优于IO-PI环流抑制器。

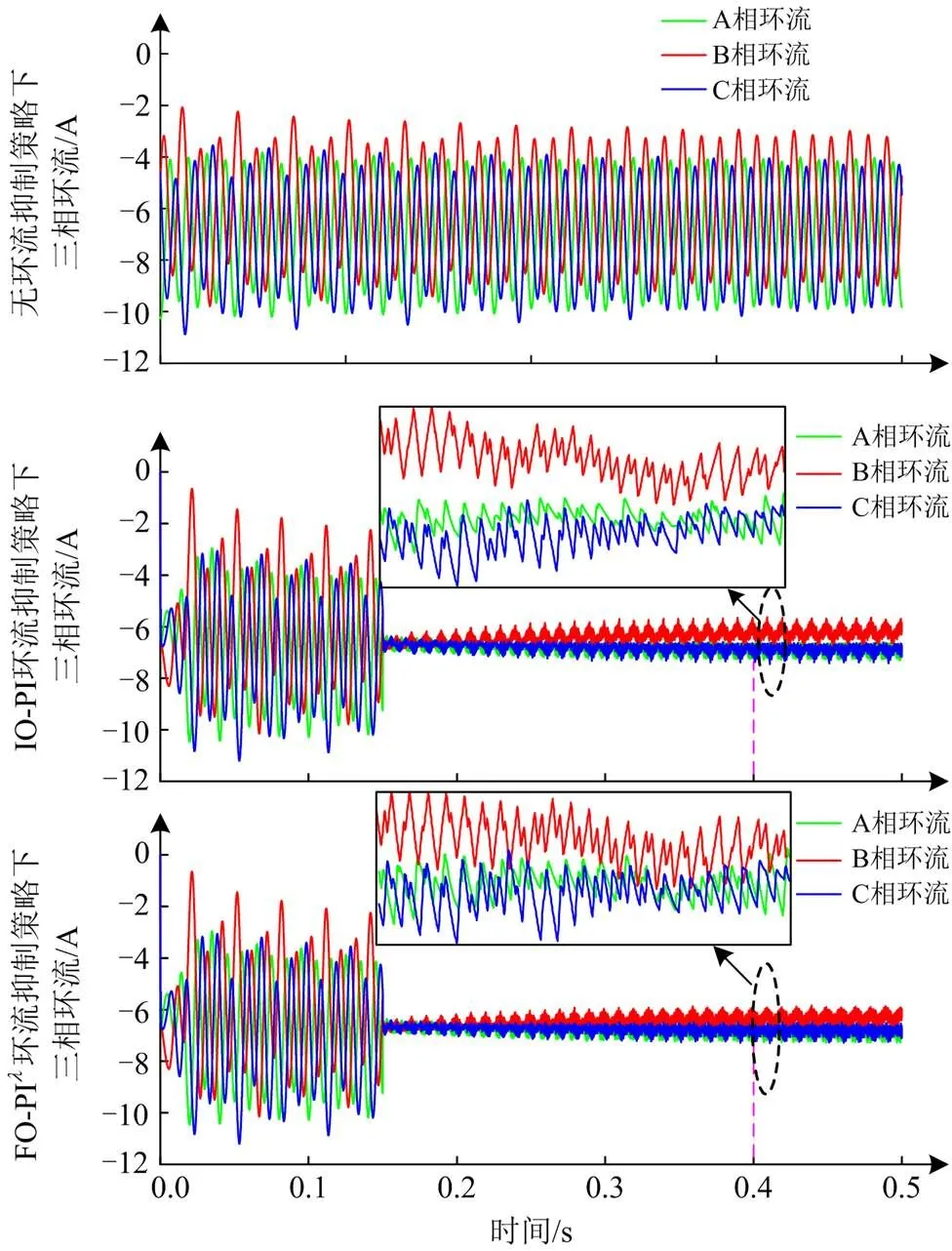
图12 三相不平衡情况下三相环流波形

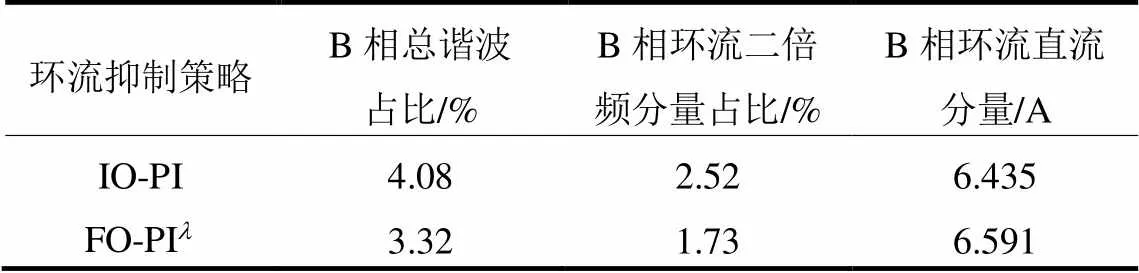
表4 三相不平衡时B相环流FFT分析

4 结论

本文基于对MMC内部环流的分析，提出基于分数阶FO-PI的环流抑制方法，并对IO-PI和FO-PI两种环流抑制器进行对比研究。通过搭建三相五电平MMC整流模型，分别对比其在交流侧加入扰动、直流电压阶跃以及三相电压不平衡情况下两种环流抑制器的环流抑制效果，并得出以下结论：

1) FO-PI环流抑制器可显著降低环流中二倍频负序分量占比和总谐波占比，并且对系统中直流分量的影响最小。

2) 在系统交流侧加入扰动前和扰动切除后，FO-PI环流抑制器控制下环流变化程度相对较小，提高了系统抗干扰能力。

3) 在直流电压阶跃和三相电压不平衡情况下，FO-PI环流抑制器的环流控制效果均优于IO-PI环流抑制器。

[1] 范明烨, 李慧, 刘思嘉, 等. 控制参数对柔性直流电网稳定性的影响分析[J]. 电力系统保护与控制, 2021, 49(21): 43-52.

FAN Mingye, LI Hui, LIU Sijia, et al. Impact analysis of control parameters on the stability of flexible DC girds[J]. Power System Protection and Control, 2021, 49(21): 43-52.

[2] 马文忠, 田洪英, 刘慧玉, 等. 非隔离型模块化多电平DC/DC变换器的最小化桥臂环流控制[J]. 电力系统保护与控制, 2021, 49(22): 51-58.

MA Wenzhong, TIAN Hongying, LIU Huiyu, et al. A minimized AC circulating control strategy for a non-isolated modular multilevel DC/DC converter[J]. Power System Protection and Control, 2021, 49(22): 51-58.

[3] YAO Zhiqing, ZHANG Qun, CHEN Peng, et al. Research on fault diagnosis for MMC-HVDC Systems[J]. Protection and Control of Modern Power Systems, 2016, 1(1): 71-77.

[4] SONG Guobing, HOU Junjie, GUO Bing, et al. Pilot protection of hybrid MMC DC grid based on active detection[J]. Protection and Control of Modern Power Systems, 2020, 5(1): 82-96.

[5] 周竞宇, 赵宇, 胡雨龙, 等. MMC-HVDC系统功率器件的结温估算与寿命预测[J]. 电网与清洁能源, 2021, 37(5): 24-32.

ZHOU Jingyu, ZHAO Yu, HU Yulong, et al. Research on junction temperature estimation and life prediction of power devices in MMC-HVDC System[J]. Power System and Clean Energy, 2021, 37(5): 24-32.

[6] 张建坡, 胡子为, 闫语. MMC-HVDC改进模型预测控制策略研究[J]. 中国电机工程学报, 2021, 41(7): 2363-2373.

ZHANG Jianpo, HU Ziwei, YAN Yu. Impact analysis of control parameters on the stability of flexible DC girds[J]. Proceedings of the CSEE, 2021, 41(7): 2363-2373.

[7] 徐雷, 夏向阳, 敬华兵, 等. 基于勒让德多项式的MMC自适应反步控制策略[J]. 中国电力, 2022, 55(3): 18-27.

XU Lei, XIA Xiangyang, JING Huabing, et al. Adaptive back-stepping stability control strategy for MMC based on Legendre polynomial[J]. Electric Power, 2022, 55(3): 18-27.

[8] 张烜一, 江修波, 郑文迪, 等. 基于电阻耗能支路的MMC-HVDC线路故障清除与重启恢复策略[J]. 电力科学与技术学报, 2021, 36(6): 67-76.

ZHANG Xuanyi, JIANG Xiubo, ZHENG Wendi, et al. MMC-HVDC line fault clearing and restart recovery strategy based on the resistance energy-consuming branch[J]. Journal of Electric Power Science and Technology, 2021, 36(6): 67-76.

[9] 王宁燕, 许军, 丁登伟, 等. 柔性直流输电工程中MMC模块内IGBT运行时暂态电压精确测量方法研究[J]. 高压电器, 2021, 57(9): 26-33.

WANG Ningyan, XU Jun, DING Dengwei, et al. Research on accurate measurement method of transient voltage of operated IGBT in mmc module in flexible HVDC transmission project[J]. High Voltage Apparatus, 2021, 57(9): 26-33.

[10] WICKRAMASINGHE H R, KONSTANTINOU G, POU J, et al. Interactions between indirect DC-voltage estimation and circulating current controllers of MMC-based HVDC transmission systems[J]. IEEE Transactions on Power Systems, 2018, 33(1): 829-838.

[11] 杨晓峰, 林智钦, 周楚尧, 等. 模块化多电平换流器MMC的环流抑制技术综述[J]. 电源学报, 2015, 13(6): 58-68.

YANG Xiaofeng, LIN Zhiqin, ZHOU Chuyao, et al. Survey of circulating current suppressing technologies in MMC[J]. Journal of Power Supply, 2015, 13(6): 58-68.

[12] DEBDEEP S, TANMOY B, SAURAV D. A reduced switching frequency sorting algorithm for modular multilevel converter with circulating current suppression feature[J]. IEEE Transactions on Power Electronics, 2019, 34(11): 10480-10491.

[13] 屠卿瑞, 徐政, 郑翔, 等. 模块化多电平换流器型直流输电内部环流机理分析[J]. 高电压技术, 2010, 36(2): 547-552.

TU Qingrui, XU Zheng, ZHENG Xiang, et al. Mechanism analysis on the circulating current in modular multilevel converter based HVDC[J]. High Voltage Engineering, 2010, 36(2): 547-552.

[14] 周月宾, 江道灼, 郭捷, 等. 模块化多电平换流器子模块电容电压波动与内部环流分析[J]. 中国电机工程学报, 2012, 32(24): 8-14.

ZHOU Yuebin, JIANG Daozhuo, GUO Jie, et al. Analysis of sub-module capacitor voltage ripples and circulating currents in modular multilevel converters[J]. Proceedings of the CSEE, 2012, 32(24): 8-14.

[15] 李慧, 张鹏, 刘思嘉. MMC环流抑制策略的暂态分析[J]. 电力系统保护与控制, 2021, 49(2): 30-38.

LI Hui, ZHANG Peng, LIU Sijia. Transient analysis of MMC circulating current suppression strategy[J]. Power System Protection and Control, 2021, 49(2): 30-38.

[16] YANG Limin, LI Yaohua, LI Zixin, et al. Loss optimization of MMC by second-order harmonic circulating current injection[J]. IEEE Transactions on Power Electronics, 2018, 33(7): 5739-5753.

[17] 牛得存, 孙中尉, 李楠, 等. 基于准PR控制器的MMC-HVDC新型环流抑制策略研究[J]. 电力电容器与无功补偿, 2016, 37(4): 87-94.

NIU Decun, SUN Zhongwei, LI Nan, et al. Study on MMC-HVDC new type loop current control strategy based on quasi-pr controller[J]. Power Capacitor & Reactive Power Compensation, 2016, 37(4): 87-94.

[18] 张建坡, 赵成勇. 模块化多电平换流器环流及抑制策略研究[J]. 电工技术学报, 2013, 28(10): 328-336.

ZHANG Jianpo, ZHAO Chengyong. Research on circulation current and suppressing strategy of modular multilevel converter[J]. Transactions of China Electrotechnical Society, 2013, 28(10): 328-336.

[19] 杨晓峰, 李泽杰, 郑琼林. 基于虚拟阻抗滑模控制的MMC环流抑制策略[J]. 中国电机工程学报, 2018, 38(23): 6893-6904.

YANG Xiaofeng, LI Zejie, ZHENG Qionglin. A novel MMC circulating current suppressing strategy based on virtual impedance sliding mode control[J]. Proceedings of the CSEE, 2018, 38(23): 6893-6904.

[20] HAGIWARA M, MAEDA R, AKAGI H. Theoretical analysis and control of the modular multilevel cascade converter based on double-star chopper-cells (MMCC- DSCC)[C] // The 2010 International Power Electronics Conference, 2010, Sapporo, Japan: 2029-2036.

[21] 屠卿瑞, 徐政, 管敏渊, 等. 模块化多电平换流器环流抑制控制器设计[J]. 电力系统自动化, 2010, 34(18): 57-61.

TU Qingrui, XU Zheng, GUAN Minyuan, et al. Design of circulating current suppressing controllers for modular multilevel converter[J]. Automation of Electric Power Systems, 2010, 34(18): 57-61.

[22] 张夏辉, 韩民晓, 杨景刚, 等. 直流侧电压波动对MMC的环流影响机理分析及抑制方法[J]. 电力系统自动化, 2021, 45(15): 122-131.

ZHANG Xiahui, HAN Minxiao, YANG Jinggang, et al. Analysis on influence mechanism of DC-side voltage fluctuation on circulating current of modular multilevel converter and its suppression method[J]. Automation of Electric Power Systems, 2021, 45(15): 122-131.

[23] 何一文, 许维胜, 程艳. BUCK型开关变换器分数阶PIlDm控制研究[J]. 电子测量与仪器学报, 2010, 24(2): 162-166.

HE Yiwen, XU Weisheng, CHENG Yan. Research on buck converter control based on fractional order PIlDmcontroller[J]. Journal of Electronic Measurement and Instrumentation, 2010, 24(2): 162-166.

[24] XIAO Min, TAO Binbin, ZHENG Weixing, et al. Fractional-order PID controller synthesis for bifurcation of fractional-order small-world networks[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2021, 51(7): 4334-4346.

[25] 张晓, 周康, 吴凡. 基于分数阶PIλ的MMC并网控制策略[J]. 电测与仪表, 2020, 57(18): 115-121.

ZHANG Xiao, ZHOU Kang, WU Fan. MMC grid- connected control strategy based on fractional order PIλ[J]. Electrical Measurement & Instrumentation, 2020, 57(18): 115-121.

[26] 王瑞萍, 皮佑国. 基于分数阶PI速度控制器的永磁同步电动机控制[J]. 电工技术学报, 2012, 27(11): 69-75.

WANG Ruiping, PI Youguo. Fractional-order PI speed controller for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2012, 27(11): 69-75.

[27] 张小凤, 王孝洪, 田联房, 等. 基于分数阶PI控制器的有源电力滤波器直流侧电压控制[J]. 电力系统自动化, 2013, 37(16): 108-113, 124.

ZHANG Xiaofeng, WANG Xiaohong, TIAN Lianfang, et al. DC voltage control of active power filter based on fractional-order PIcontroller[J]. Automation of Electric Power Systems, 2013, 37(16): 108-113, 124.

[28] 薛定宇. 分数阶微积分学与分数阶控制[M]. 北京: 科学出版社, 2018.

Fractional order PIcirculating current suppressing strategy for modular multilevel converter

ZHENG Zheng, LI Peike, LI Shaoling, WANG Xiaoshuai, JIN Tingting

(School of Electrical Engineering and Automation, Henan Polytechnic University, Jiaozuo 454000, China)

The system power loss and bridge arm current distortion of a modular multilevel converter (MMC) are increased by the circulating current. In view of the poor robustness and limited control accuracy of the traditional PI circulating current controller, thefractional order PIcontroller is applied to MMC circulating current suppressing. First, the working characteristics of MMC are analyzed, and the mechanism of circulating current generation is described. Second, the fractional order PIcontrol structure is studied and the fractional order PIcirculating current suppressing strategy is designed. Then, the classical frequency domain method is used to optimize the fractional order PIcontroller parameters, and the circulating current control performance of the system using traditional PI controller and fractional order PIcontroller is analyzed. Finally, under the same conditions, the system with fractional order PIcirculating current suppressing strategy and traditional PI circulating current suppressing strategy are simulated under AC power disturbance, DC-side voltage step and three-phase unbalance conditions respectively. The results show that the designed fractional order PIcirculating current controller outperforms the traditional PI circulating current controller in anti-power disturbance and circulating current suppressing, and is more suitable for nonlinear systems such as MMC.

modular multilevel converter; circulating current suppressing; fractional order FO-PI

10.19783/j.cnki.pspc.220367

国家自然科学基金项目资助(61703144)；河南省科技攻关项目资助(222102240027)；河南省高等学校重点科研项目资助(20A470005)

This work is supported by the National Natural Science Foundation of China (No. 61703144).

2022-03-20；

2022-07-13

郑 征(1965—)，女，博士，教授，研究方向为可再生新能源功率变换与并网技术、大功率电力电子与电力系统控制；E-mail: zhengzh@hpu.edu.cn

李佩柯(1998—)，男，硕士，研究方向为电力电子变换器建模与控制；E-mail: 893556984@qq.com

李绍令(1990—)，男，博士，讲师，研究方向为电力电子系统及控制技术。E-mail: lishaoling@hpu.edu.cn

(编辑 许 威)