锂电池健康度和剩余寿命预测算法研究
2023-01-31晋殿卫顾则宇张志宏
晋殿卫,顾则宇,张志宏
锂电池健康度和剩余寿命预测算法研究
晋殿卫1,顾则宇2,张志宏2
(1.国网陕西省电力公司信息通信公司,陕西 西安 710005;2.厦门大学信息学院,福建 厦门 361005)
为了实现锂电池健康状态检测和电池故障诊断,在电池全生命周期退化数据基础上,分别使用容量增量分析和差分电压分析法进行特征提取,使用皮尔逊相关系数对健康因子进行相关性分析,并将其输入到人工神经网络用于电池健康状态(state of health, SOH)预测。针对电池容量非线性的退化特性以及局部重生现象,使用双指数函数对其进行建模。同时结合粒子滤波算法对模型参数进行估计,实现电池剩余使用寿命(remaining useful life, RUL)的概率密度预测。实验结果表明所提出的方法能够实现SOH的精准预测和RUL的不确定性估计。
剩余使用寿命;电池状态检测;故障诊断;人工神经网络;粒子滤波
0 引言
随着全球变暖和传统能源危机,新能源已全面走进人们的生产生活。锂电池因具有低成本、高能量密度和循环寿命长等优势,已被广泛应用在电子设备和电动汽车等领域,但其安全性与可靠性一直是备受关注的问题[1]。
随着不断的充放电循环,电池健康状态出现下降,老化的电池会引发相应的安全问题。为防止电池过度充电和放电,并延长锂离子电池系统的使用寿命,亟需提出有效的电池管理系统[2]。电池管理系统可以对电池的健康状况进行检测。电池健康状态(state of health, SOH)指标经常被用来描述老化电池与新电池之间的差异[3],影响电池SOH的因素包括温度、放电深度和充电速率等,但这些指标不能直接表征电池的性能退化程度,并且这些指标对于在线检测存在一定困难[4]。电池本身是一个复杂的电化学系统,其内部特性与外部特征之间形成独特的关系[5]。电池实际容量是指电池在充满电的情况下所储存的电能,是能够直接表征电池寿命退化的重要参数。电池SOH由式(1)定义。
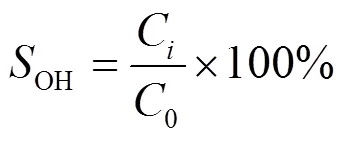
电池剩余寿命(remaining useful life, RUL)同样是电池健康程度的重要指标,它实现了对电池容量到达一定阈值的剩余可充放电循环次数的预测,对电池故障诊断进行建模预测。现有的锂电池RUL预测方法也包括两类,分别为物理模型和数据驱动模型。物理模型从电池机理出发建立数学模型。文献[11]提出了一种伪二维电化学模型,用来判断电池容量衰减程度并预测电池剩余的使用寿命。文献[12]通过对电池每次循环的充放电过程进行分析提出了一个经验模型。文献[13]将粒子滤波方法用于经验模型。数据驱动模型从电池性能退化数据出发提取特征并进行建模,从而给出预测结果。针对电池寿命数据样本比较少的电池剩余寿命预测问题,文献[14]提出了一种利用灰色模型的电池剩余寿命预测方法。文献[15-16]分别使用机器学习和深度学习的方法进行RUL预测。
电池健康状态退化过程是复杂的电化学反应过程,基于物理模型的SOH预测有明确的物理意义,但效果较差。而基于数据驱动的模型依赖于电池退化特征,现有的数据驱动文献方法构造特征缺乏实际意义,同时模型过于复杂且泛化性差。通过对电池退化过程的充放电数据进行增量容量分析(increment capacity analysis, ICA)[17]和差分电压分析(differential voltage analysis, DVA)[18]并提取健康特征,在进行相关性分析之后用于人工神经网络的SOH预测。在RUL预测上采用双指数函数对电池容量退化过程建模,使用粒子滤波算法进行函数参数估计,粒子滤波算法是一种在线预测算法,它需要不断获得观测值对参数进行修正,为了对预测过程中不确定的SOH观测值进行模拟,采用人工神经网络的预测值作为观测值。整个算法流程如图1所示。在获取到电池全生命周期退化数据后将其划分为训练集和测试集。训练集用于训练SOH预测的双层反向传播(back propagation, BP)神经网络,而后将测试集数据代入神经网络得到预测值作为粒子滤波算法的观测值模拟,因此双层BP神经网络预测效果对粒子滤波算法的参数更新有着重要的影响。算法融合了数据驱动方法和物理模型,具有很好的预测效果。该方法不易受到噪声和环境的干扰,能够实现对SOH和RUL的动态预测。算法可以快速实现且鲁棒性强。
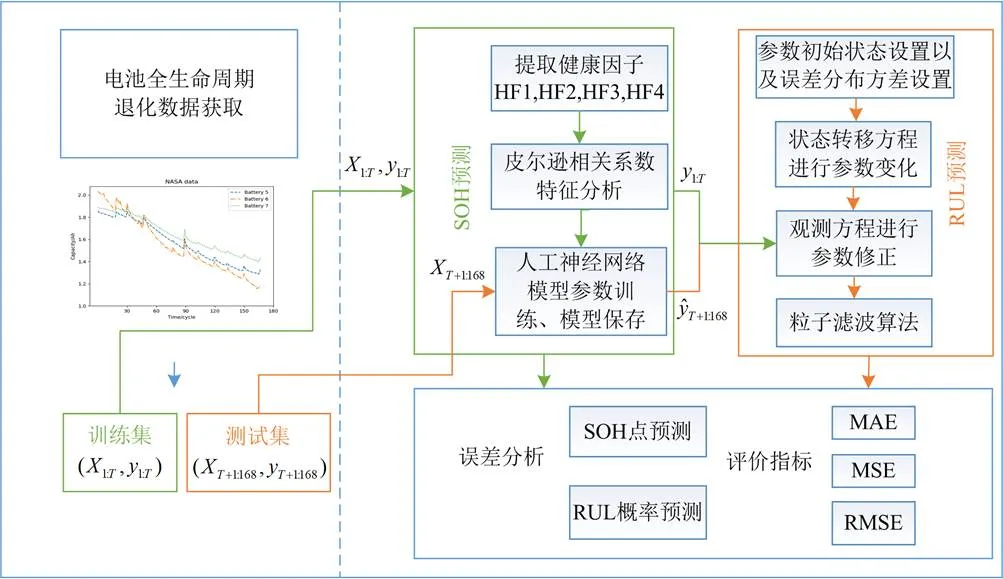
图1 锂电池SOH和RUL预测算法流程图
1 基于人工神经网络的SOH预测
1.1 数据集介绍
在预测算法之前,首先对实验用到的数据集进行介绍。实验数据来自美国航空航天局(national aeronautics and space administration, NASA)卓越故障预测中心,该中心采用额定容量为2 Ah的18650型市售钴酸锂离子电池进行循环测试,在室温下测试3种不同的电池工作曲线(充电、放电和阻抗)。
表1给出预测实验的参数,分别为环境温度(environmental temperature, ET),充电电流(charging current, CC),放电电流(discharging current, DC),放电结束电压(end of charge, EOC)和寿命结束标准(end of life charge, EOLC)[19]。一次充放电循环由充电阶段和放电阶段组成。充电阶段先进行常流充电再进行常压充电,而放电始终保持常流放电直至不同电池的EOC。重复的充放电循环是电池加速衰落的主要原因,各电池的容量变化曲线如图2所示。锂电池的容量总体上随着循环次数的增加而减少,伴有部分的上升抖动,这是受到电池容量重生现象的影响[20]。NASA数据集被广泛用于锂电池的预测算法研究[9, 21]。

表1 用于预测实验的锂电池参数
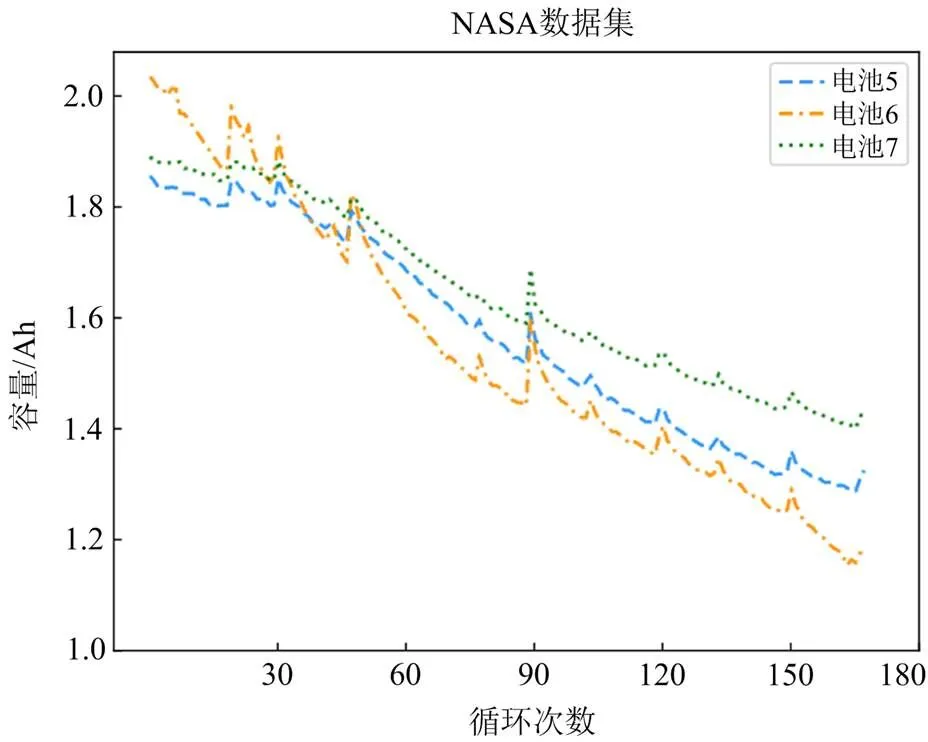
图2 电池容量的变化曲线
1.2 特征工程
1.2.1容量增量分析
基于人工神经网络的SOH预测方法需要提取与SOH有关的关键特征,也被称为健康因子(health feature, HF)。在实际应用中,电压、电流、电池环境的温度和操作时间能直接被测量和记录。从电池的原始充放电数据出发,使用ICA[17]、DVA[18]方法提取健康因子。作为一种非破坏性方法,ICA法和DVA法通过分析增量容量(incremental capacity, IC)曲线和差分电压(differential voltage, DV)曲线揭示电池老化过程中内部的变化,相对于传统的充放电曲线有着更高的灵敏度,进而更明确地分析电池内部的衰退过程和老化机理。
如图3所示,以NASA-05数据为例,在电池多个充放电循环内的常流放电阶段,电池的电压由4.2 V单调下降到EOC 2.7 V结束,但由于电池内部反映特性,电池电压会呈现加速退化趋势,假设放电量和电压之间的关系由式(2)确定。
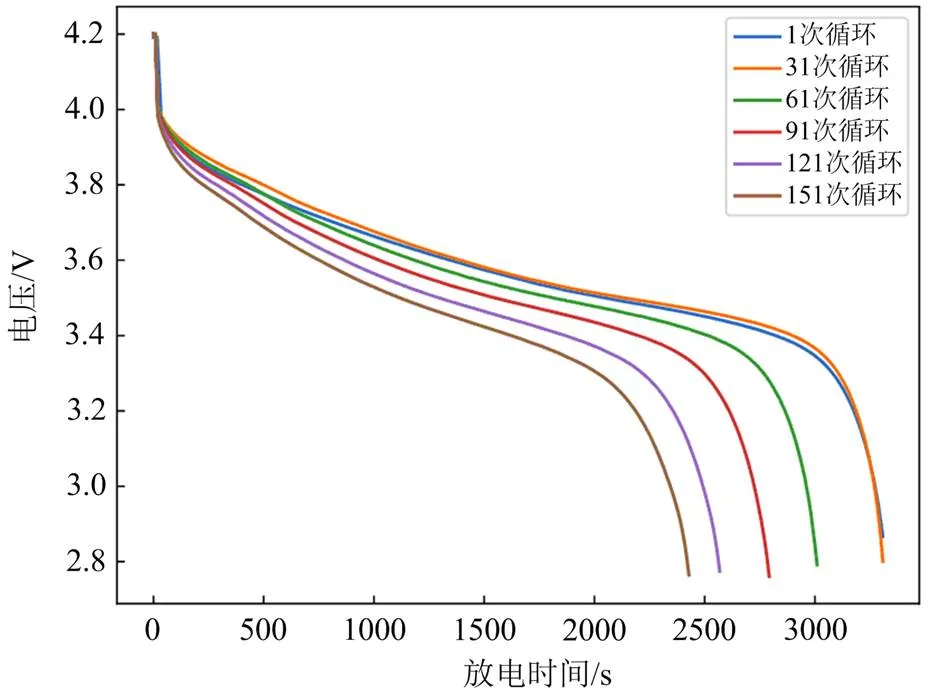
图3 电池5放电阶段的电压变化曲线
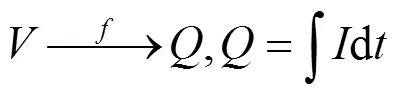
式中:表示电流;表示放电量;表示电压;表示电压到容量的映射函数。这种加速退化趋势可由映射函数的一阶导函数确定,而IC曲线刻画了增量容量d和电压d之间的比值关系,即在固定电压区间下放电量的增量。同时放电量可由电流在固定时间内的积分计算可得,给定放电过程中一个具体的电压区间,精确的IC可以通过式(3)近似计算得到。
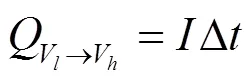
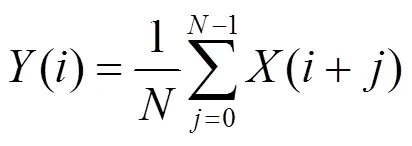
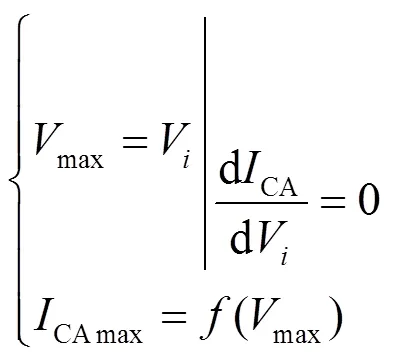
从图5中可以看到IC峰的位置和IC值随着电池充放电的循环次数增加而向左下方移动,这与电池容量都呈现相同的线性变化趋势,但31次循环处受到局部容量重生现象影响而出现上升。IC曲线中的IC峰对应于动力电池电极上的相变过程,是电池正极材料(positive electrode, PE)和负极材料(negative electrode, NE)相变过程共同作用的结果[22]。其中包括NE中锂嵌入过程将6转化为LiC6的多于5个的相变过程和PE中LiMn2O4的两个相变过程。为了准确地了解老化机制,IC曲线常常以低电流激励如/25倍率进行放电。然而在实际应用中很难使用较小的电流完成放电,NASA数据集也是1倍率下进行放电,这导致图5中只有一个非常明显的IC峰。
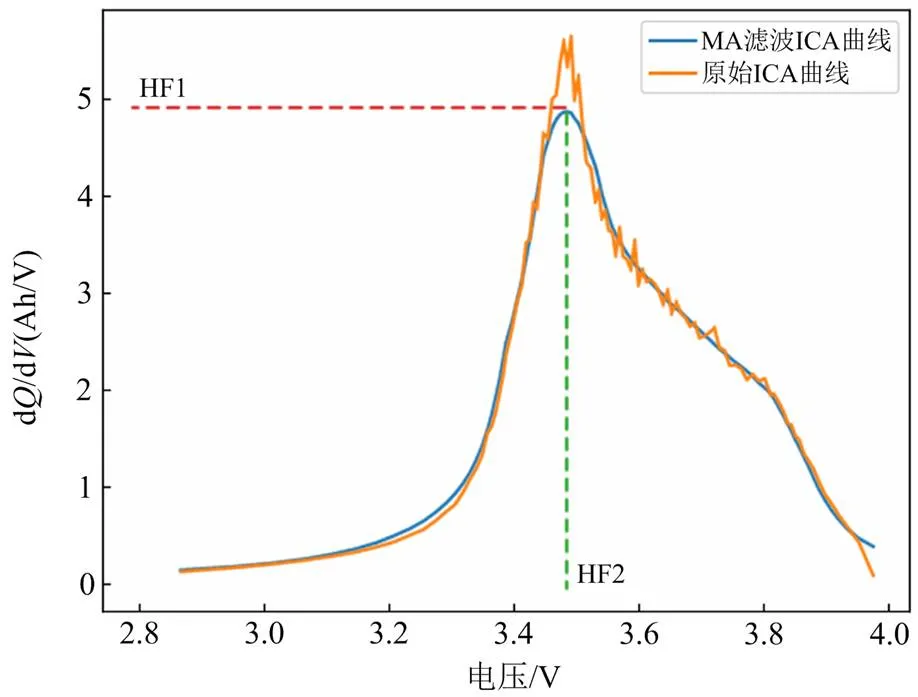
图4 电池5的ICA曲线
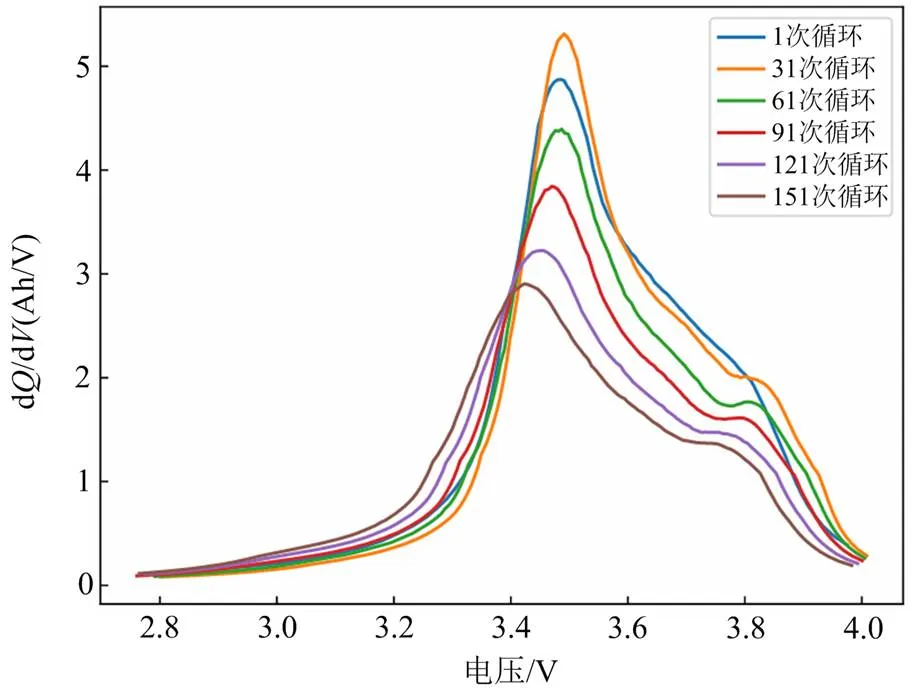
图5 不同循环下的ICA曲线
ICA法通过分析IC曲线以揭示出锂电池老化过程中其内部的细微变化,进而明确锂电池的退化过程。这也是目前离线研究锂电池退化与SOH的一个有效手段。而DVA方法则是从DV曲线出发分析锂电池的老化机理,DVA用于识别锂电池正负极活性物质损失和锂离子损失等。1.2.2节将利用DVA提取健康因子HF3、HF4。
1.2.2差分电压分析
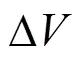
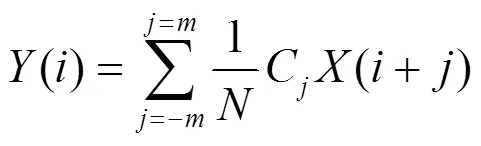
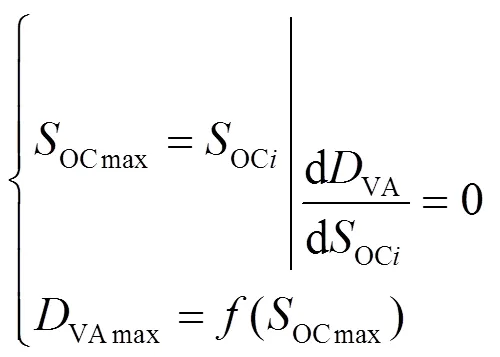
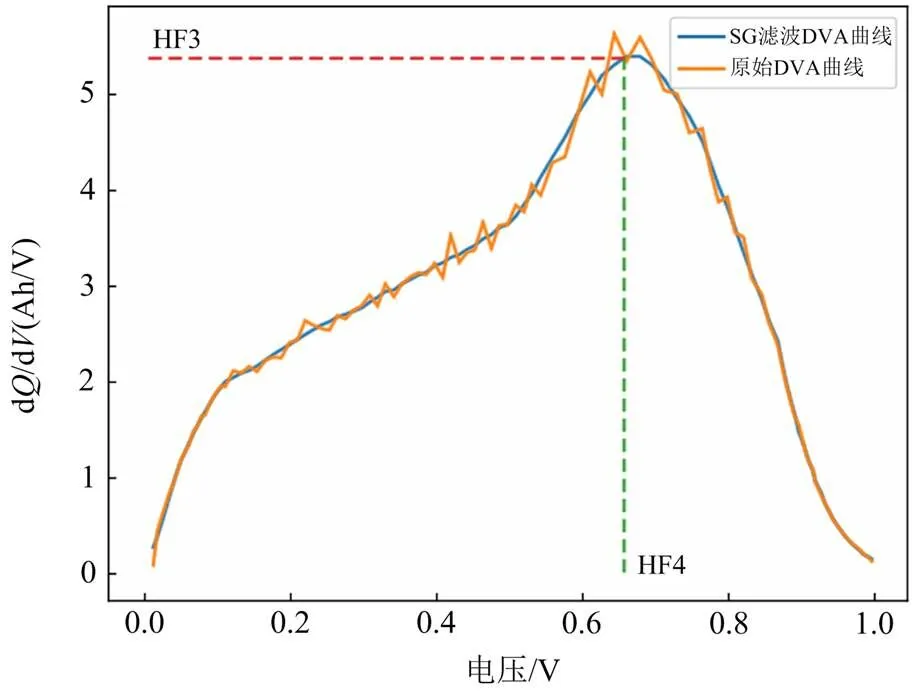
图6 电池5的DVA曲线
不同循环下的DVA曲线如图7所示,可以发现在剩余容量相对较高的区域即定义的HF3、HF4呈现明显的下降趋势,且下降趋势比剩余容量较低的区域更明显,这是因为HF3、HF4处电池容量损失除了受负极NE中活性物质损失外还存在锂离子的流失[22],而31次循环受局部重生现象出现上升。这与电池 5的容量退化曲线呈现相同的线性变化趋势。下面对健康因子HF进行相关性分析。
1.2.3相关性分析
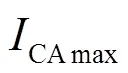
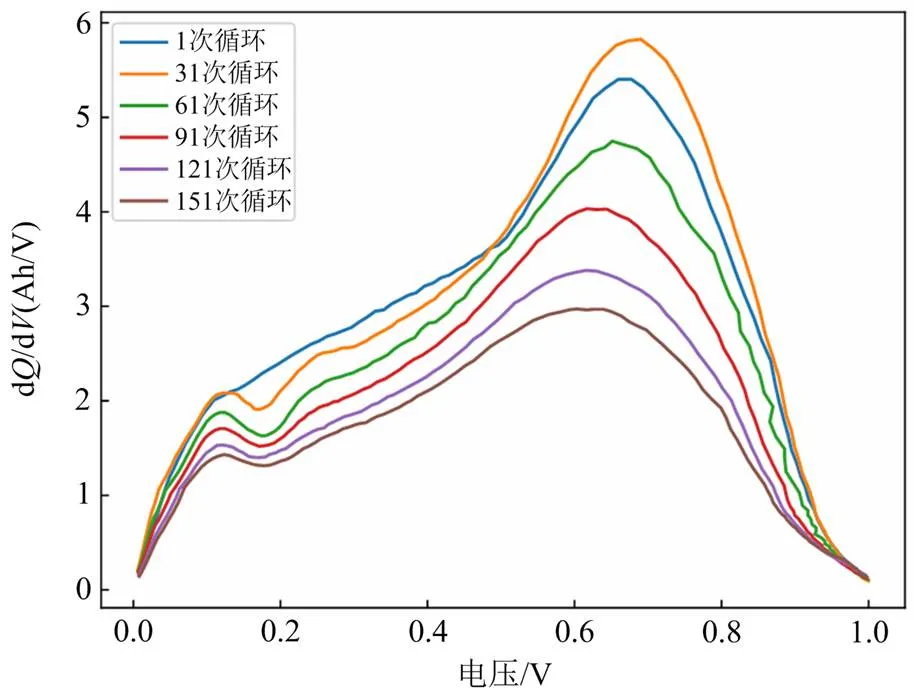
图7 不同循环下的DVA曲线
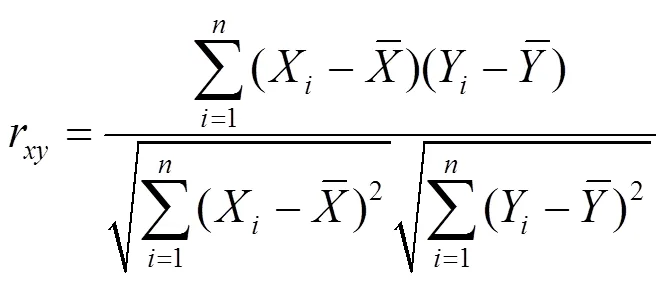
通过表2的相关性分析,健康因子与SOH之间的皮尔逊相关系数都在0.9以上,有的达到0.99以上。这表示健康因子与SOH之间有很强的相关性。健康因子向量作为神经网络预测的输入向量是有意义的。提取的健康因子和电池老化之间的映射关系可以用于电池SOH估计。

表2 健康因子的相关性分析
1.3 人工神经网络
自从第一个神经元生物学模型MP模型和BP算法诞生以来,多层前馈型神经网络已经成为应用广泛的神经网络模型[23]。如今,深度学习的快速发展使得神经网络系统理论发展迅速,以卷积神经网络(CNN)和循环神经网络(RNN)为代表的深度学习模型已经在图像识别、语音识别、时间序列预测等领域取得了巨大的成功,强化学习和图神经网络也在组合优化、图结构学习等任务上效果显著,但这些复杂的网络结构都由简单的人工神经网络演变而来。人工神经网络不需要在输入量与预测量之间建立复杂的数学模型,根据通用近似定理,BP神经网络通过对简单的非线性函数进行数次复合,可以近似任何复杂的函数。电池SOH退化过程本身是一个复杂的电化学反应系统,很难从电池机理角度进行精确建模,而人工神经网络的方法直接学习输入的健康因子(HF)与预测的电池SOH之间的映射关系,区别于CNN、RNN、Transformer等复杂的网络结构,电池充放电数据本身与图像、语音、时间序列数据不同。多层的人工神经网络在简单的网络结构基础上也能取得很好的效果。
人工神经网络建立在多层多个简单的神经元基础上,一个简单的神经元结构如图8所示。单个神经元实现了多输入向量到单输出的映射,函数定义为
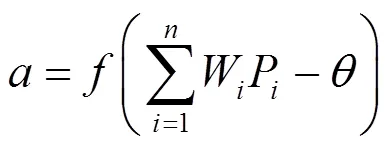
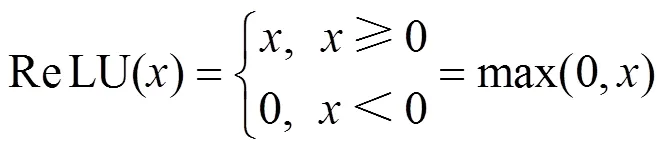
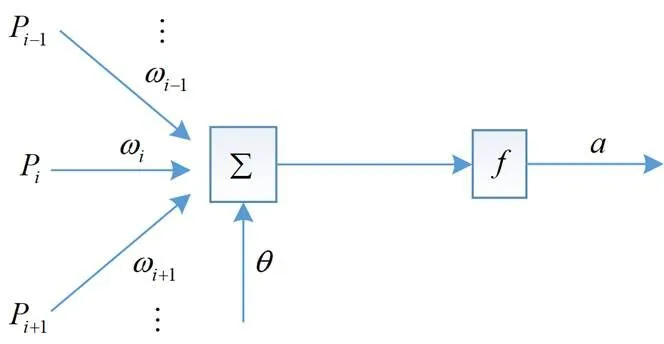
图8 神经元结构
建立的多层神经网络结构如图9所示。整个网络由输入层、输出层和隐藏层组成,隐藏层层数和神经元个数作为超参数需要人为进行调整。
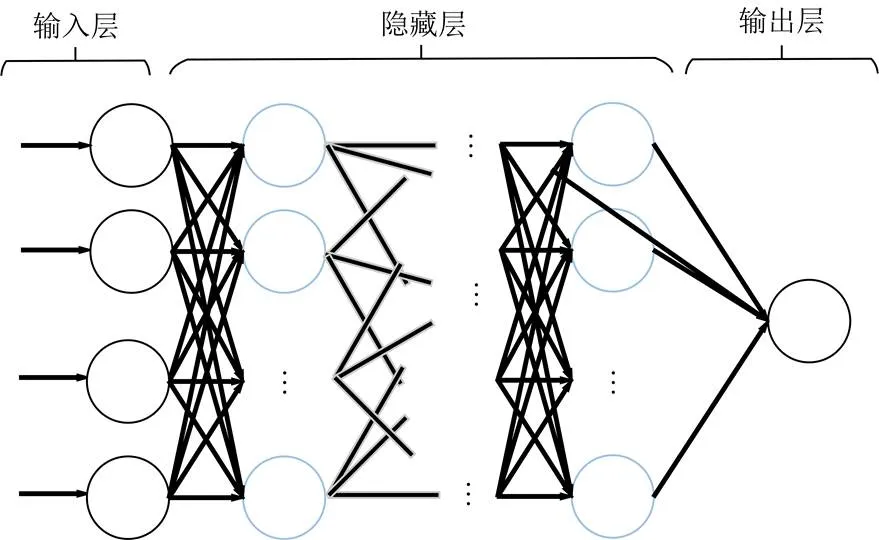
图9 多层神经网络结构
2 基于粒子滤波的电池RUL预测
粒子滤波(particle filter, PF)是一种基于贝叶斯推断的序列化蒙特卡洛方法,适用于非线性非高斯的动态系统的状态估计,而电池全生命周期退化是一个非线性的过程且电池健康状态观测值易受到噪声的干扰。PF通过生成大量粒子近似表达未知参数的概率分布情况。粒子滤波基于状态模型和观测模型(11),利用不断获取的观测值对模型参数进行更新,使得模型的参数逐渐收敛到真实值,而经典的参数估计方法将未知参数看作一组固定的未知常数,粒子滤波产生的大量粒子经过多步的更新迭代会发生退化现象,这将不足以对参数的后验分布进行刻画,一种直观的想法是给参数加入状态转移噪声。文献[9]提出了双指数函数(12)用于刻画锂电池容量退化,并得到了验证。
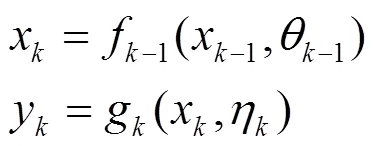

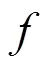
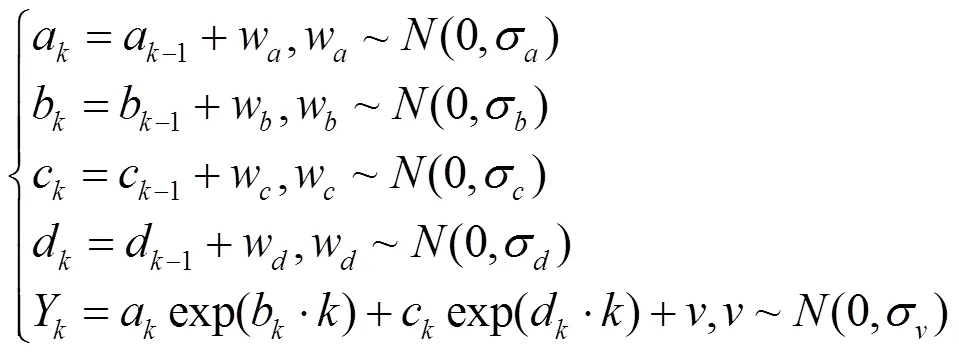
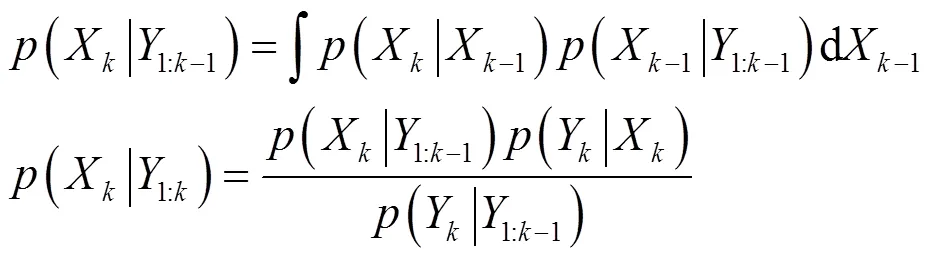
其中归一化常数由(15)计算可得,由于(15)计算涉及高维积分运算,这里采用蒙特卡洛法进行近似计算。
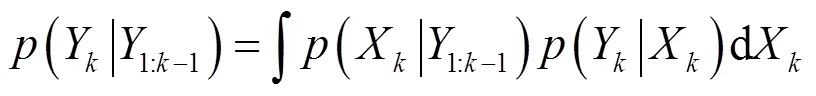
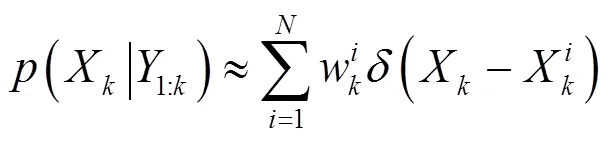
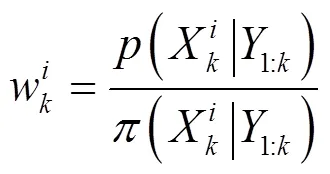
将权值进行归一化可得式(18)和权值更新公式(19)。

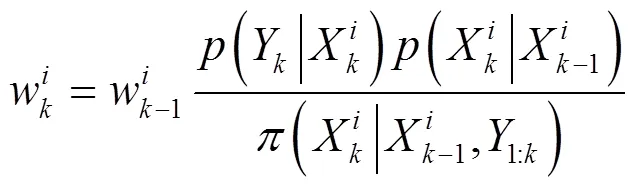
如果选择重要性函数(20)可得权值更新公式(21)。
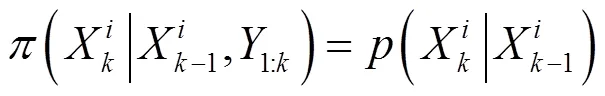
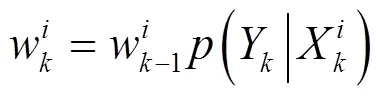
粒子滤波算法的框架图如10所示,粒子滤波算法需要不断获取的观测值对模型参数进行迭代调整,在预测阶段,电池的退化容量值无法获得,但在预测阶段,如果可以利用电池的放电数据对容量进行预测,则粒子滤波融合预测值可以得到更精确的RUL预测,所以将基于神经网络的SOH预测融合进来。在双指数函数基础上,粒子滤波算法能够实现对电池SOH退化趋势的动态追踪。由于不同电池间的容量差异,不同的电池分别设置失效阈值(end of life, EOL),EOL即为电池可接受的性能阈值,通常在额定容量的70%~80%。实际容量退化到失效阈值的循环次数与训练集划分的循环次数之间的差值为实际RUL,而粒子滤波算法不同粒子达到EOL值时循环次数则为RUL的近似分布,同时给出预测差值。
3 实验结果与分析
本文方法均采用Python语言和Keras框架实现。数据集是在2.1节介绍的NASA数据集电池5和电池7,2个电池的全生命周期都是168次循环。训练集和测试集的比例为7:3。
为了对网络结构和超参数进行调整,在训练集中采用十折交叉验证。经试验调试最终选择了双层隐藏层的BP神经网络,各电池预测模型的参数设置如下。
电池5网络参数:第一隐藏层 64个节点,第二隐藏层64个节点,激活函数 ReLU,迭代次数为200,优化方法为 Adam。
电池7网络参数:第一隐藏层 256个节点,第二隐藏层256 个节点,激活函数 ReLU,迭代次数为200,优化方法为 Adam 。
3.1 SOH预测结果
分别使用调整好的网络结构和网络参数用于NASA 电池5和电池7的SOH预测。如图11和图12所示,在118 循环往后的测试集上,双层的人工神经网络能够很好地预测电池容量退化趋势,且能够准确预测出容量局部重生点。同时使用3个评价指标MAE、MAPE、RMSE分析预测效果。如表3所示,两个电池的MAE在0.01 Ah以内。同时MAPE、RMSE的结果也表明预测结果并没有显著的异常点。
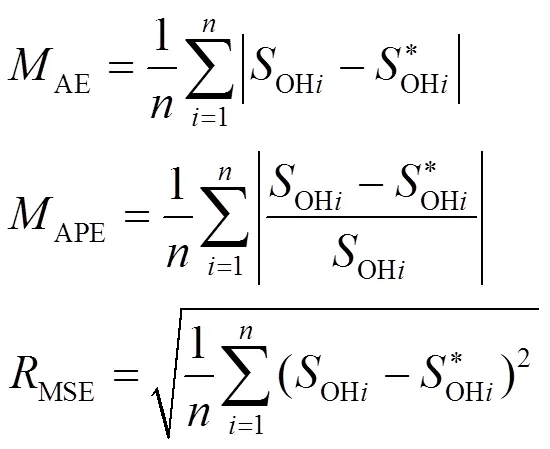
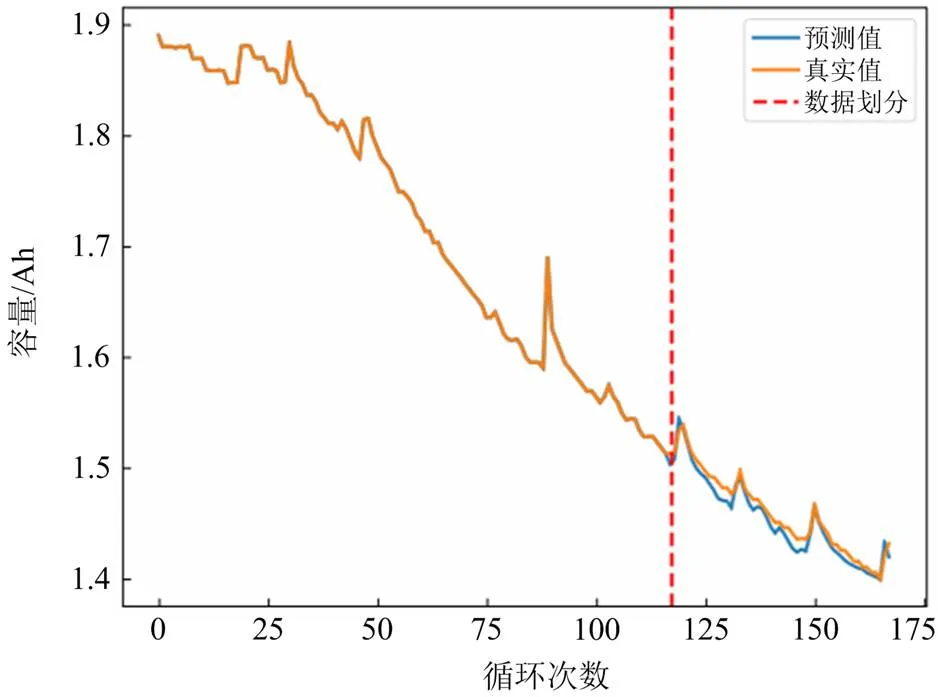
图12 电池7的容量预测

表3 电池容量预测的误差分析
3.2 RUL预测结果
指数函数的参数初值由Python库scipy中的最小二乘求解器leastsq函数确定,分别用双指数函数对电池5、6、7、18的容量退化曲线进行拟合,用最小二乘法进行参数确定。电池18也是NASA实验的电池数据,但是它的充放电周期只有138次循环,所以在做SOH和RUL预测时并不包括电池18。而电池6的拟合效果较差亦排除。
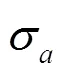
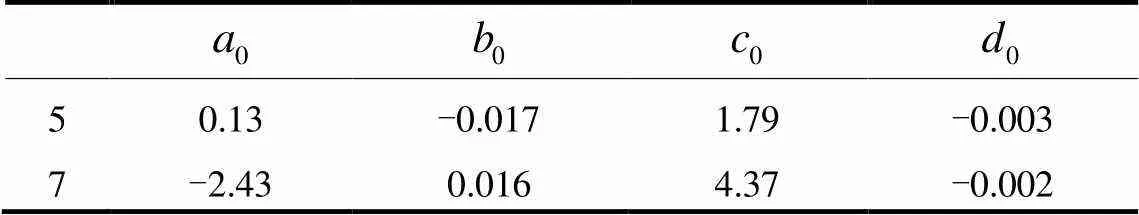
表4 参数初值设置
不同粒子达到EOL值时得到不同的循环值,进而可以得到RUL的概率密度分布。NASA数据不同电池的容量退化不同,设置电池5和电池7的EOL分别为1.30、1.40。图13和图14分别给出电池5和电池7粒子滤波的RUL预测结果。由于粒子表示的参数向量不同,且受到噪声的影响,RUL的真实值与粒子滤波算法的最大后验概率估计之间有一定的误差。但电池5、7的平均预测误差分别约为1.598次循环、0.053次循环,这表明基于粒子滤波的RUL预测算法是准确的。RUL的概率密度分布与不同粒子到达EOL的循环频率分布近似,由Python库scipy中的高斯核密度估计计算得到。同样给出密度分布的0.05分位数点和0.95分位数点并由粒子的频率分布给出90%的概率预测区间。从图13和图14可以看出RUL真实值都分布在预测区间内,这也为电池使用者进行不确定性分析提供了借鉴意义。
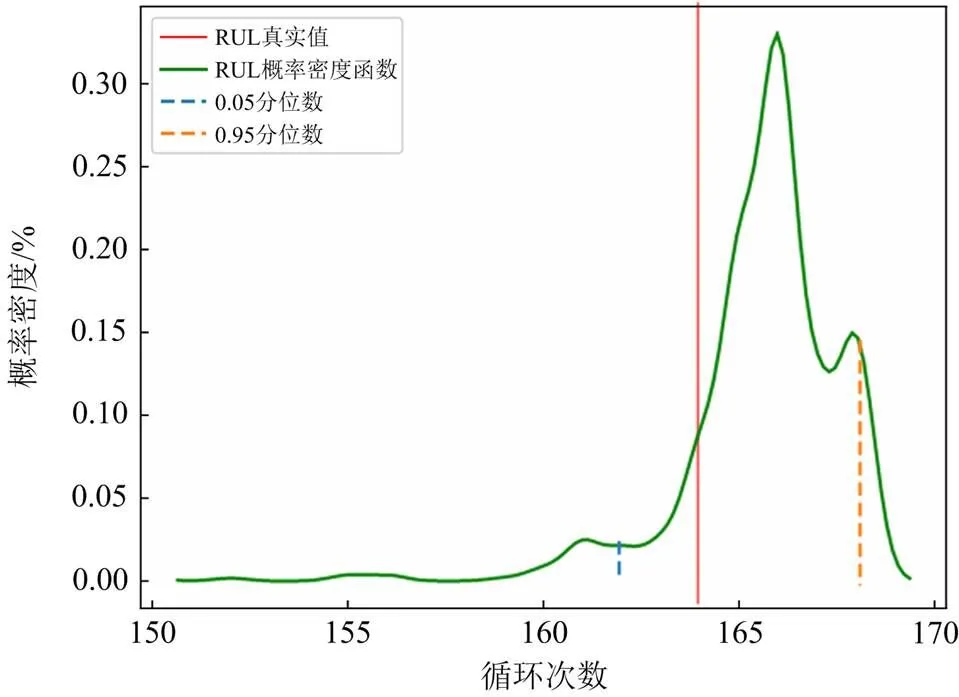
图13 电池5的RUL预测
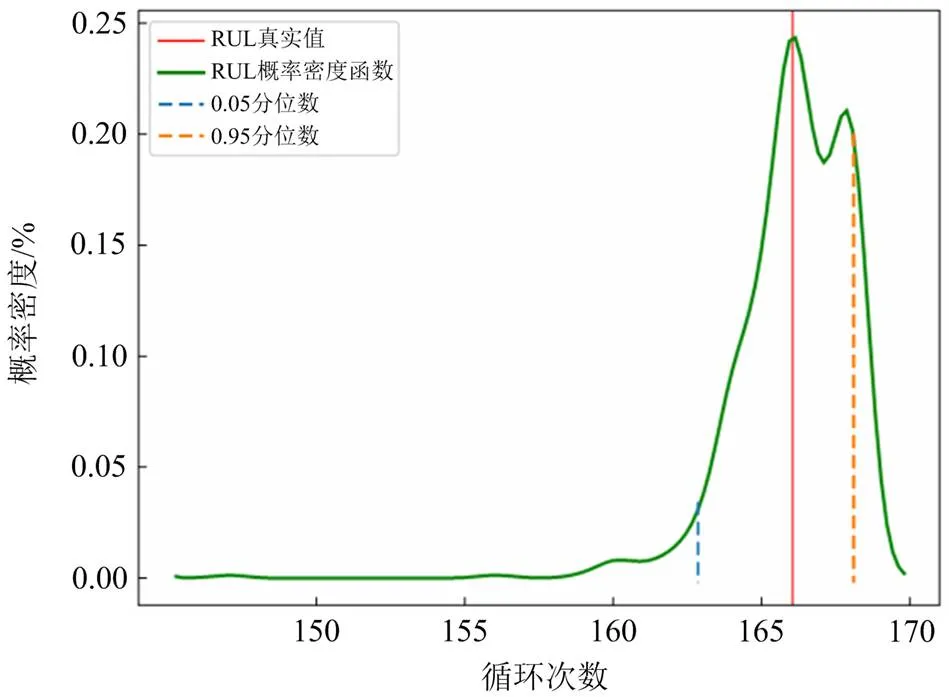
图14 电池7的RUL预测
4 结论
本文在数据驱动和机理模型的基础上对锂电池SOH与RUL进行建模预测,SOH预测方法利用信号处理的特征处理方法,提取出4个锂电池容量退化的健康因子,在对健康因子进行相关性分析之后将其用于人工神经网络的输入,而训练的人工神经网络能够精确地预测电池SOH值。
另一方面在RUL任务预测时,将粒子滤波方法用于双指数容量退化函数上,并结合人工神经网络的预测结果从而给出准确的RUL预测值。
最后在NASA数据集上验证了算法的有效性。预测算法能够实现对锂电池的健康状态检测以及故障诊断,下一步将进行大量的电池仿真实验。
[1] LU Languang, HAN Xuebing, LI Jianqiu, et al. A review on the key issues for lithium-ion battery management in electric vehicles[J]. Journal of Power Sources, 2013, 226: 272-288.
[2] 赵伟, 袁锡莲, 周宜行, 等. 考虑运行寿命内经济性最优的梯次电池储能系统容量配置方法[J]. 电力系统保护与控制, 2021, 49(12): 16-24.
ZHAO Wei, YUAN Xilian, ZHOU Yixing, et al. Capacity configuration method of a second-use battery energy storage system considering economic optimization within service life[J]. Power System Protection and Control, 2021, 49(12): 16-24.
[3] 黄健, 李建林, 李征. 退役锂离子电池健康状态快速评估方法[J]. 电力系统保护与控制, 2021, 49(12): 25-32.
HUANG Jian, LI Jianlin, LI Zheng. A state of health rapid assessment method for decommissioned lithium-ion batteries[J]. Power System Protection and Control, 2021, 49(12): 25-32.
[4] VERBRUGGE M, TATE E. Adaptive state of charge algorithm for nickel metal hydride batteries including hysteresis phenomena[J]. Journal of Power Sources, 2004, 126(1/2): 236-249.
[5] 张洋, 陈浩, 郭波, 等. 锂离子电池剩余寿命在线预测[J]. 机械科学与技术, 2016, 35(8): 1286-1290.
ZHANG Yang, CHEN Hao, GUO Bo, et al. Online prediction of remaining useful lifetime for lithium-ion batteries[J]. Mechanical Science and Technology for Aerospace Engineering, 2016, 35(8): 1286-1290.
[6] PATTIPATI B, SANKAVARAM C, PATTIPATI K. System identification and estimation framework for pivotal automotive battery management system characteristics[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2011, 41(6): 869-884.
[7] 张朝龙, 赵筛筛, 章博. 基于因子分析与K-means聚类的退役动力电池快速分选方法[J]. 电力系统保护与控制, 2021, 49(12): 41-47.
ZHANG Chaolong, ZHAO Shaishai, ZHANG Bo. A fast classification method based on factor analysis and K-means clustering for retired electric vehicle batteries [J]. Power System Protection and Control, 2021, 49(12): 41-47.
[8] WU Ji, WANG Yujie, ZHANG Xu, et al. A novel state of health estimation method of li-ion battery using group method of data handling[J]. Journal of Power Sources, 2016, 327: 457-464.
[9] LIU Datong, PANG Jingyue, ZHOU Jianbao, et al. Data- driven prognostics for lithium-ion battery based on Gaussian process regression[C] // Proceedings of the IEEE 2012 Prognostics and System Health Management Conference, May 23-25, Beijing, China: 1-5.
[10] DONG Hancheng, JIN Xiaoning, LOU Yangbing, et al. Lithium-ion battery state of health monitoring and remaining useful life prediction based on support vector regression-particle filter[J]. Journal of Power Sources, 2014, 271: 114-123.
[11] ASHWIN T, CHUNG Y, WANG Jihong. Capacity fade modelling of lithium-ion battery under cyclic loading conditions[J]. Journal of Power Sources, 2016, 328: 586-598.
[12] SAHA B, GOEBEL K. Modeling li-ion battery capacity depletion in a particle filtering framework[C] // Annual Conference of the Prognostics and Health Management Society, September 27-October 1, San Diego, California.
[13] AN D, CHOI J, KIM N. Prognostics 101: a tutorial for particle filter-based prognostics algorithm using Matlab[J]. Reliability Engineering & System Safety, 2013, 115: 161-169.
[14] GU Weijun, SUN Zechang, WEI Xuezhe, et al. A new method of accelerated life testing based on the grey system theory for a model-based lithium-ion battery life evaluation system[J]. Journal of Power Sources, 2014, 267: 366-379.
[15] SEVERSON K, ATTIA P, JIN N, et al. Data-driven prediction of battery cycle life before capacity degradation[J]. Nature Energy, 2019, 4:383-391.
[16] REN Lei, ZHAO Li, HONG Sheng, et al. Remaining useful life prediction for lithium-ion battery: a deep learning approach[J]. IEEE Access, 2018, 6: 50587-50598.
[17] WU Yitao, XUE Qiao, SHEN Jiangwei, et al. State of health estimation for lithium-ion batteries based on healthy features and long short-term memory[J]. IEEE Access, 2020, 8: 28533-28547.
[18] BLOOM I, WALKER L K, BASCO J K, et al. Differential voltage analyses of high-power lithium-ion cells. 4. cells containing NMC[J]. Journal of Power Sources, 2010, 195(3): 877-882.
[19] 胡天中, 余建波. 基于多尺度分解和深度学习的锂电池寿命预测[J]. 浙江大学学报(工学版), 2019, 53(10): 1852-1864.
HU Tianzhong, YU Jianbo. Life prediction of lithium-ion batteries based on multiscale decomposition and deep learning[J]. Journal of Zhejiang University (Engineering Science), 2019, 53(10): 1852-1864.
[20] OLIVARES B E, MUNOZ M A C, ORCHARD M E, et al. Particle-filtering-based prognosis framework for energy storage devices with a statistical characterization of state-of-health regeneration phenomena[J]. IEEE Transactions on Instrumentation and Measurement, 2013, 62(2): 364-376.
[21] ZHOU Jianbo, LIU Datong, PENG Yu, et al. Dynamic battery remaining useful life estimation: an on-line data-driven approach[C] // 2012 IEEE International Instrumentation and Measurement Technology Conference Proceedings, May 13-16, 2012, Graz, Austeia: 2196-2199.
[22] 熊瑞. 动力电池管理系统核心算法[M]. 北京: 机械工业出版社, 2018.
[23] 刘凯. 基于改进BP神经网络的短期负荷预测研究[D]. 南京: 河海大学, 2005.
LIU Kai. Short-term load forecasting based on improved BP neural network[D]. Nanjing: Hohai University, 2005.
Lithium battery health degree and residual life prediction algorithm
JIN Dianwei1, GU Zeyu2, ZHANG Zhihong2
(1. State Grid Shaanxi Information and Telecommunication Company, Xi’an 710005, China;2. School of Informatics, Xiamen University, Xiamen 361005, China)
To detect the health of lithium batteries and for battery fault diagnosis, and based on battery life cycle degradation data, increment capacity analysis and differential voltage analysis are used to extract features. The Pearson correlation coefficient is used to analyze the correlation of health factors. Health factors are input into an artificial neural network for battery state of health (SOH) prediction. From the battery capacity nonlinear degradation characteristics and its regeneration phenomenon, a dual exponential function is used to model it. A particle filter algorithm is used to estimate model parameters and achieve the probability density prediction of remaining useful life (RUL). The experimental results show that the proposed algorithm can achieve accurate prediction of SOH and uncertainty estimation of RUL.
remaining useful life; battery status detection; fault diagnosis; artificial neural network; particle filter
10.19783/j.cnki.pspc.211447
国家自然科学基金面上项目资助(62176227);国家自然科学基金智能电网联合基金重点支持项目资助(U2066213)
This work is supported by the General Project of National Natural Science Foundation of China (No. 62176227).
2021-12-27;
2022-01-19
晋殿卫(1967—),男,硕士研究生,从事电池健康状态预测、人工智能、大数据技术的研究工作;
顾则宇(1998—),男,硕士研究生,研究方向为电池健康度分析与人工智能技术;
张志宏(1986—),男,通信作者,博士,副教授,研究方向为人工智能与大数据技术。E-mail: zhihong@xmu.edu.cn
(编辑 周金梅)
