基于改进蚁狮算法优化考虑交易成本的M-CVaR模型
2023-01-31林擎鑫王一成
林擎鑫 马 宁 王一成 成 晨
(西北民族大学中国民族信息技术研究院 甘肃 兰州 730000)
0 引 言
随着现代投资组合理论的不断完善与发展,如何保证在风险最低化的同时实现收益最大化成为了研究的热点。针对直接利用Markowitz提出的基于均值-方差决策模型解决上述问题存在的模型中一系列严格假设导致了无效资产组合以及均值-方差相同的组合,受偏度影响,其风险程度可能存在较大差异等不足之处[1-3],研究者们对如何优化投资模型开展了深入研究。高岳林等[4]在均值-方差模型的基础上增加了风险以及条件风险价值作为约束条件,并建立了相应模型,结合我国股票市场实情开展了实证分析,证明了方法的合理性及优势性;黄东宾等[5]在M-CVaR模型的基础上引入偏好强度,建立了基于偏好强度的M-CVaR模型,通过分析验证了所提方法对于多位数据的整合以及资产选择能力上所具备的优势。上述方法其主要内涵是通过增加约束条件实现对于传统方法的改进,这些改进虽然起到了积极意义,却忽略了交易成本带来的影响,使得模型在一定程度上脱离了我国证券市场的实际情况。同时,交易成本作为市场中重要摩擦因素,对于投资结果产生深远的影响,因此必须予以考虑。为了达到考虑成本因素且具备较小计算代价的目的,就需要对组合投资模型中的算法进行优化。王怀柱[6]结合改进遗传算法进行CVaR模型求解,通过改进遗传算法的变异算子提高了模型收敛速度,从而达到了节约计算时间的目的;见静等[7]提出了结合动态粒子群算法对于M-VaR进行求解的思路,并结合实证分析表明该算法相对于传统算法在效率以及精度上存在的优势。一些智能算法替代传统算法,但容易陷入局部最优解,且求解效率较差[8-9]。
综上所述,为了从根本上解决上述问题,本文提出基于改进蚁狮算法优化考虑成本因素的组合投资模型。该模型在传统模型的基础上引入二次分段凹交易成本,建立了更为具体的组合投资模型;同时,针对蚁狮算法提出相应的优化方案,以提高其探索能力、收敛速度,并避免陷入局部最优解。利用上述模型结合多种证券投资组合进行分析,证明了模型在稳定求解的同时,可以保证求解过程的高效、高精度特性,从而为投资者提供更好的决策参考。
1 模型建立
1.1 CVaR模型的建立与计算
CVaR即条件风险价值,表示了在一定的置信水平下,投资者可对于未来某一时间所承担的且超过VaR均值的损失进行预测[10]。其数学表达式为:
VaRβ+E[L(w,r)-VaRβ|L(w,r)>VaRβ]
(1)
式中:w=(w1,w2,…,wi,…,wn)T,wi表示第i种资产的投资比例;r=(r1,r2,…,ri,…,rn)T,ri表示对应的i种资产的收益率;L(x,r)表示损失函数;β表示置信度。
对于CVaR而言其计算的核心在于解决损失函数带来的问题,故而依据损失函数是否连续,可以把CVaR的计算分为连续性和离散型,具体计算如下。
(1) 连续型计算。记p(r)为概率密度函数,其表示投资组合的收益率,则:
(2)
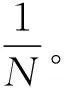
(3)
上述方法表征了对于CVaR的具体计算。但是,在实际应用过程中还需对其中的重要参数进行选择,以求达到对于不同风险偏好的投资者在承受低风险的同时,其收益最大化的目的。在这一过程中,置信水平以及对应产品的投资期限的选择对于投资组合问题的解决具备重要意义。前者不仅体现了投资者的风险偏好程度,同时还表征了计算结果的有效性,其选取决定于CVaR的计算目的;后者表征了计算期限,主要决定于资产流通性、回报率的分布特性和约束条件等因素;两者共同决定了VaR的取值。
1.2 考虑交易成本的M-CVaR模型
交易成本是指实际证券交易过程中的各种摩擦因素,其中要分为固定成本以及间接成本[11]。对于中国证券交易市场而言,固定成本是交易成本最直接的体现。其具体表达式为:
(4)
通过式(4)可以发现交易成本是一个二次分段凹函数且与资产投资比例呈正相关。
1.2.1模型假设
为了使得建立的模型更加符合我国证券交易市场的实际情况,本文进行如下假设的条件的建立。
(1) 投资者均为理性投资人假设。
(2) 价格对于价值准确反映的假设,即投资者之间进行公平竞争,竞争过程中不产生间接成本,产品价格直接体现产品的真实价值。
(3) 收益分布假设。结合文献可以发现,我国证券交易市场的收益率分布特征符合拉普拉斯分布,即其概率密度与分布性质分布表示为:
(5)
(6)
(5) 最小单位以及最大交易量约束;前者以整手为约束,后者按照相关规定单个基金对于同一家上市公司股票的持有小于其净资产的10%。
(6) 不允许出现买空卖空的现象。
1.2.2模型建立
设一个投资人共投资了n种风险资产以及一种无风险资产,其中单个风险资产的收益率记为ri(i=1,2,…,n);第i类资产的购买数Si(i=1,2,…,n),无风险资产购买数记为S0;无风险资产收益率记为r0;第i类资产的投资比例为;第i类资产的股票单价记为Pi;投资组合的总收益率记为r;初始财富记为R0,末期财富记为Rm,则有:
(7)
(8)
(9)
同时,第i种资产的权重以及投资组合的收益率分别表示为:
(10)
(11)
通过上述计算过程,组合收益的期望与方差可以表示为:
(12)
式中:σij表示不同资产的协方差。
综合上述内容并结合式(2)和式(3)以及拉普拉斯假设,引入ε作为投资者的风险承受极限,同时考虑本文研究目的在于求解投资者低风险下收益最大化模型,故而基于交易成本的M-CVaR模型为:
(13)
(14)
0≤Si≤μi,且Si⊆Z
式中:μi表示第i类资产的最大交易约束。
Crystal将抒情诗定义为“以一种短小、如歌的形式,抒发作者内心主观思想和情感的诗歌”。[5]从抒情诗歌的定义来看,抒情诗歌有明显的文体特点:体裁短小精悍、韵律节奏感强、表达诗人的内心情感和主观感受。除此之外,抒情诗歌还有一些较明显的特点,如修辞的使用。
上述模型是一个非线性模型,求解时存在精度和效率的双重困扰,故而本文将引入改进蚁狮算法对其进行求解,以求高效、高精度实现对于模型的求解。
2 改进蚁狮算法
蚁狮算法相对于蚁群算法、遗传算法等智能算法由于其考虑了蚂蚁游走与蚁狮捕食蚂蚁的双重行为,因此对于复杂问题具备更强的适应性[12-13];同时,由于该算法具备少量调节参数,因此使得其实现更为容易。但是,蚁狮算法也存在固有缺陷,主要体现为容易陷入局部最优解、搜索能力不足、求解时具备较慢的收敛速度[14-15]。对上述缺点,本文提出改进蚁狮算法,其主要思路是在传统蚁狮算法的基础上引入相应策略,从而提高算法的整体性能。
2.1 传统蚁狮算法的原理
传统的蚁狮算法其基本原理是模拟蚁狮捕食幼蚁的自然行为。该算法按如下过程开展[16-17]:
(1) 利用式(15)进行初始解的随机生成,同时,对所有蚁狮的适应度进行计算和排序,其中适应度最高的视为最优解即为精英蚁狮,记为RE。
Xn.m=La+rand(Lb-La)
(15)
式中:Xn.m表示蚂蚁位置且初始时刻蚂蚁位置与蚁狮位置相同;La、Lb分别表示蚂蚁游走可行域的上下限。
(2) 根据式(16)计算蚂蚁游走的位置。
Xi=[0,cumsum(2r(1)-1),cumsum(2r(2)-1),…,
cumsum(2r(n)-1)]
(16)
式中:Xi表示蚂蚁位置;cumsum表示蚂蚁游走位置的累积和;n表示最大迭代步数;r(n)表示随机函数,按式(17)计算。
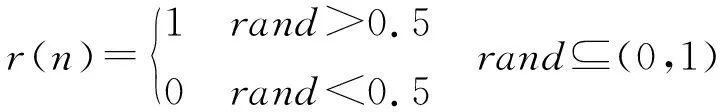
(17)
为了确保每一只蚂蚁的随机游走过程都在可行域的范围内进行,还需要对蚂蚁的位置进行离差,其具体计算如下:
(18)
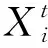
(19)
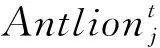
(20)
式中:w为常数,按式(21)取值;t与T分别表示当前迭代次数与最大迭代次数。
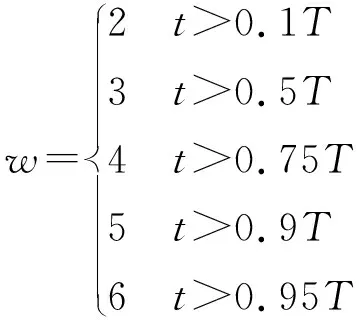
(21)
(3) 对围绕蚁狮RA与精英蚁狮RE游走的蚂蚁产生的随机位置进行更新;
(22)
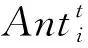
(4) 如果在随机游走的蚂蚁中,出现某只蚂蚁的适应度高于蚁狮,则视作该蚂蚁被蚁狮捕获,此时,蚁狮会根据该蚂蚁的位置更新其自身位置,重构陷阱,其数学表达式为:
(23)
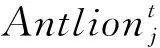
(5) 检验迭代次数是否达到最大,若是则输出最优解,反之重复上述步骤直至最优解产生。
2.2 基于不同策略下蚁狮算法的优化
本文主要通过以下两种策略进行蚁狮算法的优化:
(1) 边界策略。通过对传统蚁狮方法的计算过程进行分析,我们可以发现随着迭代次数的增加,蚂蚁围绕蚁狮走的可行域在逐渐减小,而对于同一轮迭代中呈线性分段变化趋势的蚂蚁,其游走边界完全相同。这种方法一定程度上降低了算法的多样性与随机性,不易于全局最优解的获取。本文对于式(20)进行如下改进:
(24)
这种方法使得I值随着迭代次数的增加由线性递增转变为非线性随机自适应递增,由式(24)可知,边界将按非线性随机自适应递减,这就使得相对于传统方法,蚂蚁围绕蚁狮游走更具备多样性与随机性,从而提高了算法的全局搜索能力。
(2) 选择策略。传统的蚁狮方法其选择策略为轮盘赌策略,但这种策略难以保证所有蚂蚁都围绕着较优蚁狮游走。因此,本文将预备参加轮赌选择的蚁狮按适应度值从大到小排序,同时设定只有当适应度值F满足式(25)时,蚁狮参与轮盘赌。
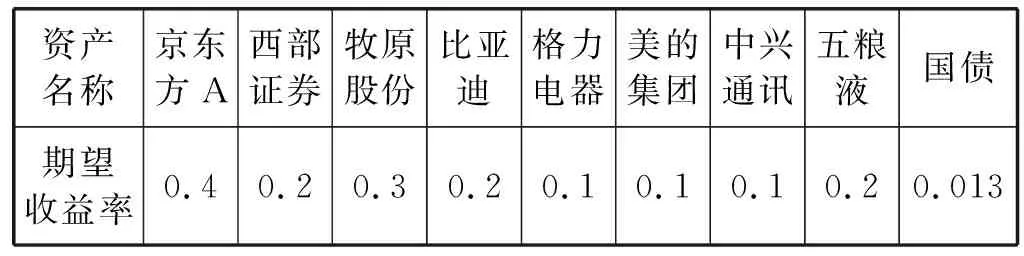
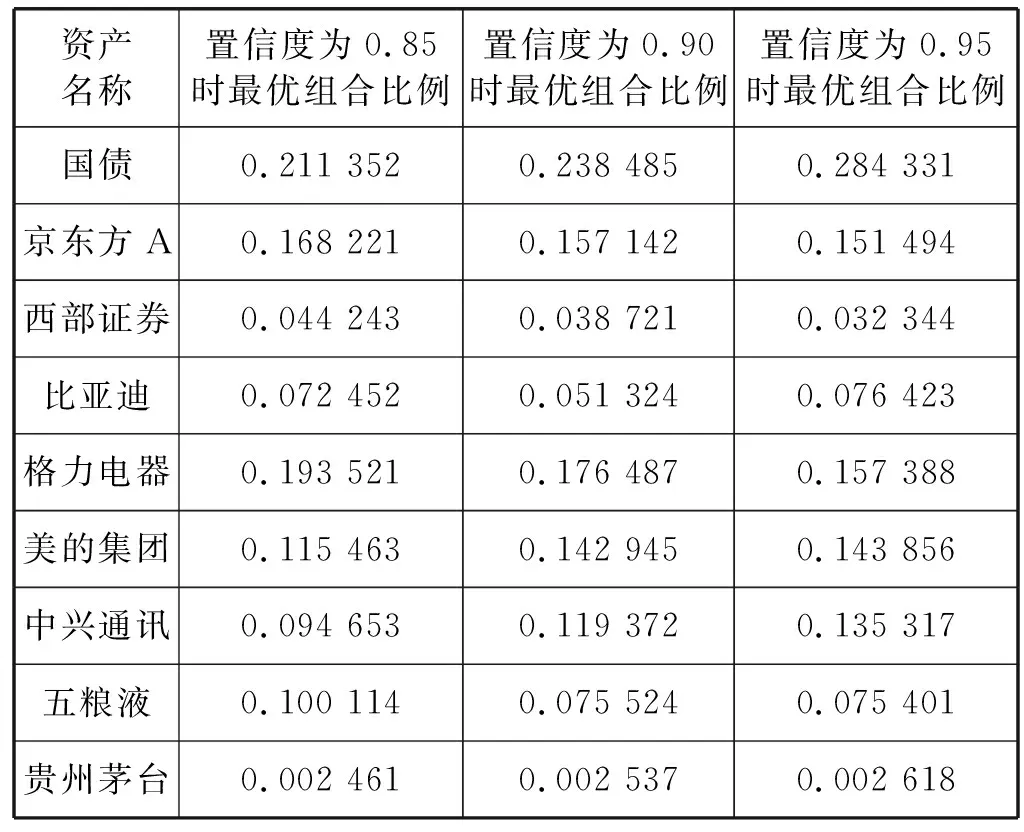
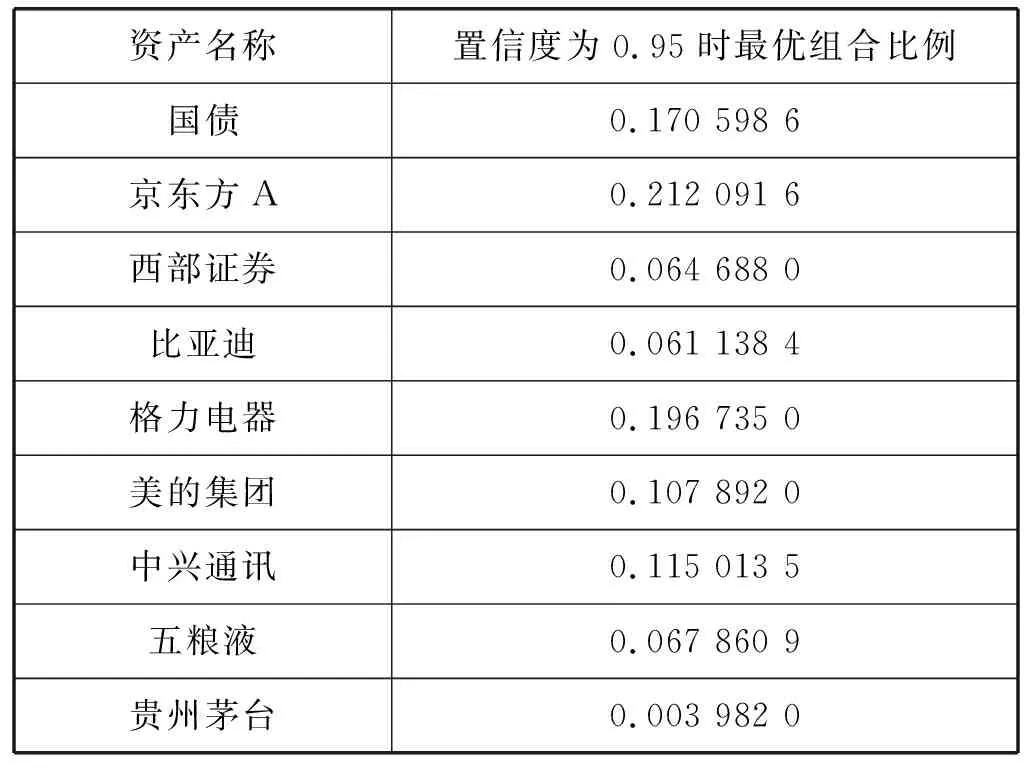
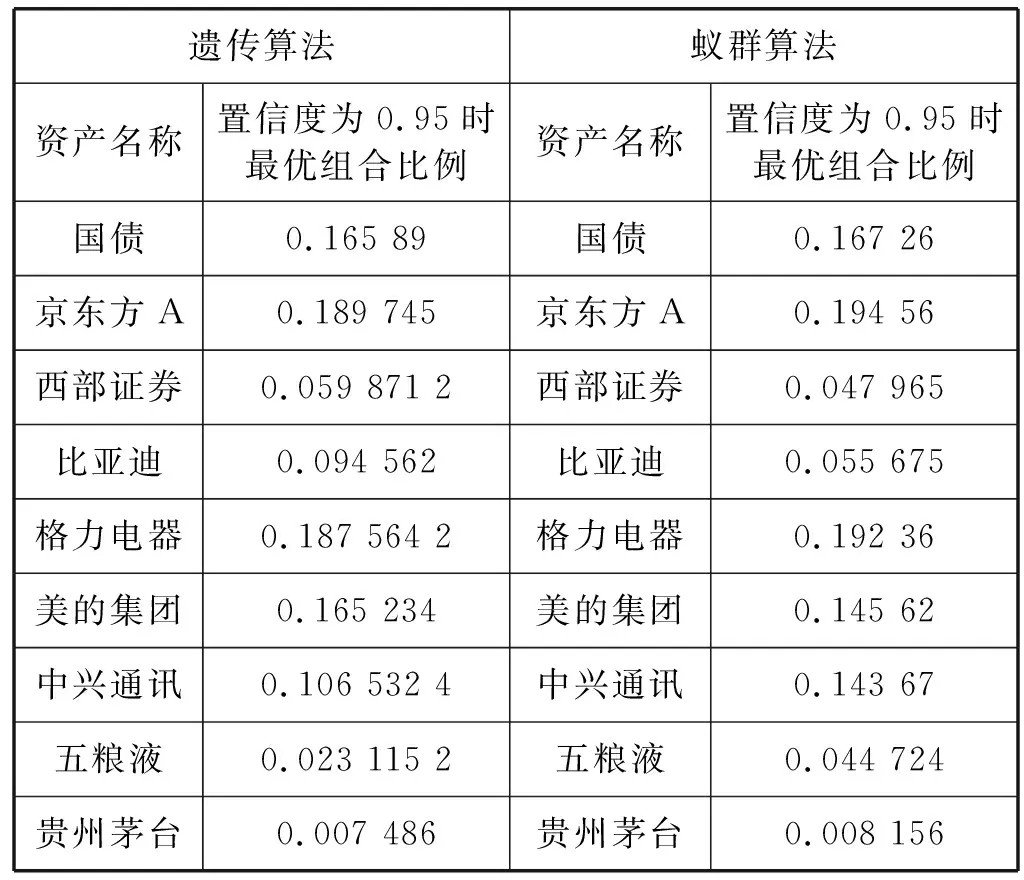
F (25) 式中:P为预备蚁狮适应度的平均值。 这种方法,提高了轮赌的门槛,在一定程度上保留蚁狮的同时,加大了蚂蚁围绕较优蚂蚁走的概率,从而提高了算法的性能。在优化考虑交易成本的M-CVaR模型时,适应度函数与目标函数的关系可以用式(26)表示。 (26) 通过对我国证券市场的实情进行分析可以发现多数投资者会选择支付成本更大的积极策略进行相关的投资以求在控制风险的同时,获得更大的利益。故而,本节将建立考虑交易成本的M-CVaR模型并结合改进蚁狮算法求解最优资产组合,同时,在这一过程中验证考虑成本因素的积极意义以及算法的有效性。 为了更有效地证明求解模型的有效性,以近期热门的券商、科技、新能源和农业等作为股票选取的题材,具体如下:京东方A(000725)、西部证券(002673)、牧原股份(002714)、比亚迪(002594)、格力电器(000651)、美的集团(000333)、中兴通讯(000063)、五粮液(000858)和一种无风险资产,本文选择国债为例;同时,所有股票数据来源于“万得咨询”。 假设初始投资为1 000万元,数据取2019年8月16日至2019年10月18日共计10个交易周来进行数据监测,得T=10。通过实际数据调研,不存在停盘以及复盘现象。 按照M-CVaR模型求解的相关需求,对以下参数进行详细说明: (1) 风险值。设置最大承受风险系数δ=0.05。 (2) 置信水平。其选择受多因素约束,为了保证计算的有效性要求置信水平较低;为了更准确反映投资者的风险偏好,则需要选择相对较高的置信水平。为了更有效地对问题进行说明,同时为了展开相应的比较分析,本文取置信水平β为0.85,0.9,0.95。 (3) 交易成本。根据假设,交易成本仅考虑固定交易成本,按2.5计算。 (4) 无风险资产。以短期贴现的国家债券为例,其2019年利率水平为0.013%,故而r0=0.013%(以天为计算单位)。 (5) 收益率。前人的分析中仅考虑算术平均收益率,这种方式忽略了资本的时间价值同时会出现上倾现象,因此本文提出使用几何平均收益率克服上述问题。通过计算,资产的期望收益率如表1所示。 表1 资产期望收益率(%) 3.3.1模型计算 通过计算,考虑成本因素的计算结果如表2所示。 表2 考虑成本因素的最优投资组合 可以看出,改进蚁群算法对于求解考虑成本因素的M-CVaR模型有效性。同时,由于置信水平的选择体现了投资者的风险偏好程度,投资者可以根据自身情况选择合适的置信度组合进行投资。如果投资者厌恶风险,则选择置信度高的组合进行投资,如果投资者对风险厌恶程度低,可选择置信度低的组合。结合我国实际证券市场,在后面的分析中置信度均取0.95。因此,在置信水平为0.95时,不考虑成本因素的投资最优组合如表3所示。 表3 不考虑成本因素的最优投资组合 3.3.2数据分析 在置信度为0.95时,考虑成本因素的实际收益为451 802元;不考虑成本因素的实际收益为393 145元;因此可以说明在风险系数δ=0.05时,考虑成本因素计算出来的最优投资组合收益有95%的可能要高于理论综合效益;而不考虑成本因素的实际收益值则小于理论综合收益。综上所述考虑交易成本的模型对于最优组合的求取更具备意义。 传统智能算法如遗传算法、蚁群算法等在求解模型时也被广泛应用,基于遗传算法与蚁群算法对于模型求解的结果如表4所示。 表4 遗传算法与蚁群算法的计算结果 由不同方法在置信度为0.95时的计算结果可以发现,改进蚁狮子算法的求解结果优于遗传算法与蚁狮算法,且其求解效率也高于遗传算法与蚁狮子算法,因此对于考虑成本因素的M-CVaR模型该算法具备更好的适用性。同时,该算法不需要对金融变量的分布以及市场参数做其余假设,避免了求解时的情景限制,因此其适用于对于多种风险度量下带现实交易条件的投资组合问题,相对于其余算法更具备普遍性。 本文为了解决有限资产的条件下,对具有不同风险收益特征的证券进行配置的问题,首先建立了考虑交易成本的M-CVaR投资组合模型;其次,引入了改进蚁狮算法对于该模型进行求解;最后,通过对多种证券展开实证分析,证明了改进蚁狮算法求解的可行性以及考虑考虑交易成本对于求解最优投资组合求解的积极性与必要性。目前的研究都假定投资者为理性经济人,如何应对投资人为非理性情况的研究将是未来继续研究和努力的方向。
3 实证分析
3.1 数据预处理
3.2 参数设定
3.3 数据结果分析
3.4 方法对比
4 结 语
