受限水平狭缝中液桥的形貌和毛细力计算

马姝靓,程震宇,阳 丽

(广西师范大学 物理与科学技术学院,广西 桂林 541004)

对于混凝土、裂缝岩石这样的连续孔隙介质，当窄缝孔隙中渗透入一定量的雨水或者灌溉水等液体时，孔隙水压力的变化会引起固体的微小形变，其力学特性也会随之发生变化[1].例如，对于平行固体之间的狭缝，液体在孔隙中会形成小液柱(称为液桥)，孔隙之间填充形成的液桥会产生静态毛细管力和动态黏附力，使得土壤、岩石之间孔隙减小渗透率降低，这是土壤渗流中的一个重要规律.充分理解裂缝性多孔介质中的液体运移现象是成功描述许多工业过程的关键，如采油[2]、农业灌溉和排水[3]、印刷或涂层过程[4]、清洁应用中与多孔材料相连接的液体吸芯[5]、电子元器件的微型化封装过程[6]等.因此，研究液体量和液体形貌变化对天然气管道输运、微机电系统、微电子组装、土壤和岩石力学行为的影响具有十分重要的意义.

目前，对于两固体平面间的静态液桥结构，学者们大都采用有限元、有限体积软件、蒙特卡罗模拟、分子动力学软件等进行数值模拟或简化理论计算分析[7-13].例如，Van Gols-Racht[7]研究裂缝中形成稳定的液体桥的条件，认为如果裂缝孔径在50 μm以上，就无法实现沿一堆基质块的毛细管连续性，毛管连续现象是裂缝性油藏原油渗流和裂缝性含水层污染物运移的重要原因.Dejam等[8]通过形成液桥模拟了多孔基质块之间的毛细管连续性，认为裂缝毛细管压力和块体间的相互作用会显著影响岩石基质块体中物质的运移.Broesch等[9]利用Surface Evolver软件仿真狭长裂缝几何形状中非轴对称毛细管桥的形态演变，对比模拟和实验关于扎钉角随着高度变化的结果，发现理论结果随着板间距的增加出现了偏差，认为这是由于模拟中的3个假设导致毛细桥的平均曲率被高估了.Dejam等[10]对平行狭缝间液体桥的静态形状进行了理论研究，提出了一种新的无量纲分析杨-拉普拉斯方程，其中液体桥表面的形状可以用α和β表示为定义的无量纲参数，得到了描述液桥气液界面变化的积分，并对其进行了数值求解.朱朝飞等[11]通过张力等效方法建立液桥的三维受力模型, 采用不考虑重力的球形近似求解液桥形态微分方程，研究狭长平行板间液桥的形态特征参数随着接触角、接触长度和宽度等形态方面的参数变化的规律，以及液桥毛细力大小的变化，并将理论结果与Surface Evolver软件仿真结果对比.张昭等[12]研究平行的片状颗粒之间的液桥从形成到断裂的毛细力的演化规律，并分析液桥形成时毛细力与液桥体积和固体接触角的关系.杜凡等[13]关注平行板间薄液层的退缩和瞬间断裂过程，观察到液体的柱对称形态，并计算了断裂过程中液体内部或液体与固体之间的力.

国内外学者主要关注的是(不受限)无限大的固体平面间的液桥，现有模型多为等径/不等径球形双颗粒模型、球形-平面模型、平面平行固体表面模型、圆柱-平面模型、圆锥-平面模型等[14].出于计算简便，液桥一般近似为圆柱形状，即将液桥的形态近似为以半弧形液桥绕中心轴线旋转一周形成的三维形状(圆环假定)[15].关于固体平面间液桥的研究还需考虑几个问题：首先，环形近似使得液体桥表面有非恒定平均曲率，这与杨-拉普拉斯方程不一致[16]，而且环形近似只对于足够小的液体体积和分离距离的液桥是准确的；其次，对于狭缝中的液体，固体平面提供了一个基本的约束空间，在平板几何中流体被限制(受限空间)在两个平行的平面固体壁面之间；最后，实验中观察到具有一定宽度的狭缝间的液桥并不是规则的圆柱体，而是呈现出类马鞍形状[17-18].因此，有必要对受限空间，例如狭缝间液桥的形貌曲面规律进行深入研究.本文以拉普拉斯方程为理论基础，采用椭圆弧几何近似法，对受限平行狭缝间的液体形貌特征参数进行数值计算，推导出液桥体积和毛细力的计算公式，从而探究受限空间和不受限空间内液桥的形貌变化规律的区别.

1 模型和计算方法

图1为水平裂缝之间液桥的简化模型，θ是固液接触角，α是三相接触线的钉扎角，Rn为两端液面最细处宽度.以裂缝宽度方向为X轴，长度方向为Y轴，以此建立三维直角坐标系，M(xm，ym，zm)为液面轮廓线上任意一点.rc、rd分别为液桥侧面和端面的曲率半径，H是裂缝表面间距，W为裂缝宽度.模型基于3个假设：1)将狭缝简化为一对平行的不考虑表面粗糙度的平面；2)不考虑重力作用，液桥形态呈现轴对称分布；3)两端液面最细处的“颈部”半径为狭缝宽度的一半.随着两板间距的变化，液固界面宽度受狭缝长度方向的边界约束保持不变，但液桥会沿着狭缝长度方向自由地伸长缩短，即液桥具有平动的不变性.液桥的形貌随上下狭缝平面间距的变化而不同.

图1 水平裂缝中的液桥模型

1.1 液桥体积的计算

液桥的力学特征取决于其表面几何形状，因此需要对液桥表面形貌进行准确的计算.由于液桥中段和两端的形状各异，因此液桥总体积为两部分之和：

V=Vtwo ends+Vmiddle,

(1)

液桥的两端呈现类马鞍形状，弯月面的轮廓呈现弧形，因此任意一点M的坐标为：

ym=Rn+rd-rdsin(β1+θ),

zm=rd[cosθ-cos(β1+θ)],

其中两端和两侧角度的积分微元取值范围分别为β1∈[0,π-2θ],β2∈[0,π-2α].将液桥三相接触线在xy二维平面内采用椭圆方程描述(椭圆弧假定)[15-16]，通过数值积分可以得到液桥两端体积为[19]：

(2)

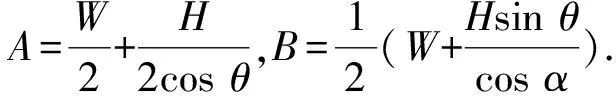
液桥中段的体积[20]为：

(3)

其中Ly表示中段润湿长度，可通过计算系统的总能量(包括液气、固液和固气接触面)，然后根据能量最小化原理得到

(4)

将式(2)～(4)代入式(1)中，可将液桥的总体积表示为α的函数表达式.假定液体在短时间内不可压缩，并忽略蒸发，则液桥的体积在狭缝空间内不变.当γ、θ、V、H、W等参数可测量时，可以求得液桥的形貌特征参数α和Ly的数值，进一步得到液桥上任意一点M的坐标，从而掌握液桥的所有几何特征值.

1.2 毛细力的计算

毛细力是毛细压力差和表面张力共同作用的结果，这与液桥的几何形状和润湿特性有关.通过计算液体作用于固体表面的压力和表面张力可以得到，即液桥在竖直方向上受到液气界面内外压差产生的拉普拉斯力FL(沿着固体被湿润区域的液桥轴线方向)和液气界面张力在轴线方向上的分量FT(在三相接触线上沿着液桥轴线方向).总的毛细力可以写为

(5)

其中：Ω表示液体与上部固体接触的润湿区域的表面积,lu表示上部固体表面三相接触线的长度，ΔP为液桥内外界面压力差(毛细压力)，ΔP=Pin-Pout.可根据杨-拉普拉斯方程计算得到

(6)

(7)

其中：γ是液体表面张力系数,rd和Rn是两个正交方向的主曲率半径,rd=H/(2cosθ),这里规定若半径在液桥内部，则其符号为正;若半径在液桥外部，则其符号为负.在没有重力的情况下，ΔP为常数，它的值由H、θ决定.

三相线上液体表面张力引起的拉力在液桥轴线方向的作用力FT为：

FT=γlu,

(8)

将式(6)～(8)代入式(5)可得(液桥力)毛细力表达式为：

(9)

2 模型验证

下面基于本文的理论模型对影响狭缝内的液桥形貌的参数进行研究.影响参数包括液桥体积V、板块宽度W、接触角θ、液桥高度H、表面张力γ，液桥几何特征参数钉扎角α、Ly和M的坐标值直观反应了液桥的形貌.当V、W、θ、γ、H的数值通过实验测量得到之后，利用matlab求解隐式方程组(1)～(4)即求解得到α的数值，继而得到M的坐标和Ly的数值.再通过式(9)得到相应的毛细力的结果.

首先关注狭缝的关键参数H、W、θ对α、Ly的影响.图2(a)将等式(5)的计算结果与实验结果[9]的H-α曲线进行对比，点状为实验结果，实线为计算结果，可以看到两者具有很好的一致性.但是当狭缝间距较大的时候，计算值与实验值之间出现了微小误差，这可能是由于重力引起的液桥不对称情况导致的，本文模型中并未考虑到重力引起的液桥形变.从图2(a)中看出，在低于H时，α是锐角，随着H的增加，α变为钝角，差不多增大到160°左右.因此钉扎角的变化主要划分为3个范围：70°<α<90°，α=90°和90°<α<180°.钉扎角的增加与平均曲率从凹(负)到凸(正)的过渡有关.图2(b)显示弯月面的变化示意图，其中暗含液桥侧面曲率的变化.当α为锐角的时候，侧面曲率rc为正值，平均曲率为负值，液面内凹.当α为钝角的时候，侧面曲率rc为负值，平均曲率为正值，液面外凸.α增加意味着液桥弯月面随着间距的增大由凹(concave)变为矩形框(rectangular box)，最后变凸(convex).这是因为狭缝中的液桥随着距离的增加，其长度同时在收缩(图2(c))，液桥逐渐变短变粗.同样的狭缝宽度时，体积越大，液桥长度越长.同样的体积时，宽度越小，液桥越长.其次关注液体接触角对α的影响.图2(d)给出了改变接触角时H-α变化曲线.从图中可以发现，接触角对液桥的形貌影响也比较大.在同一个体积和宽度下，接触角越大，随着H的增加，α角越大，即液桥两侧越凸.液桥的两端形状能直观的反应出触角的影响，在亲水情况下，即θ小于90°时，液桥两端弯月面一直为凹液面;在疏水情况下，即θ大于90°时，液桥两端弯月面一直为凸液面[16].

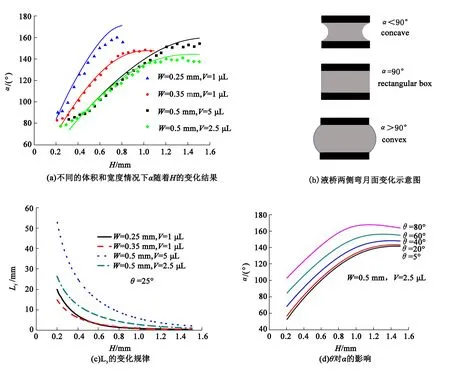
图2 理论计算结果(温度25 ℃，纯水表面张力γ=0.072 75 N/m)

3 毛细力的计算结果

在相对较大的体积和较小的分离距离下，根据式(5)计算得到毛细力的关系曲线.为定性表示结果，将毛细力采用无量纲处理，可知任意体积、宽度、表面张力等条件下毛细力.图3(a)显示了无量纲毛细力以及其中的两项随H/W的变化趋势.可以看出毛细力与单独参数V、H、W无关，与H/W和θ的比值密切相关.此结果与文献[9]中有限元软件Surface Evolver软件模拟数值结果一致，验证了本文理论分析的正确性.

图3 毛细力理论计算结果

图3(a)结果显示Fcap、FL、FT随着液桥狭缝体积宽度比的增大而减小.在不同的体积或宽度情况下,Fcap、FL、FT几乎相等，这与Valencia等[17,21-22]的模拟结论一致.图3(a)表明F-H/W曲线明显表现出两个阶段，即随着间距增大而减小的(绝对值)快速下降阶段和最后趋于平缓阶段.当距离较小时，Fcap、FL、FT下降趋势较快；当距离较大时，下降趋势减缓.当F为负值(negative)的时候，液桥两侧弯月面呈现凹形(图2(b)中concave)，液桥表现为毛细引力，液桥的存在使得狭缝上下平面相互联结，F值越大，液桥的稳定性越好.当F为正值(positive)的时候，弯月面呈现凸形，液桥力为毛细斥力.狭缝间的毛细连结作用会受到液桥的稳定性降低的影响而减弱.

分别计算出毛细力中的FT和FL,可以看到，FL这项的正负值取决于ΔP的符号.当H增加时，附加压力ΔP指向液面的曲率中心，当液面为凹液面时为负值，凸液面时为正值.相应的FL曲线有3个特征阶段，随着距离的增加其值(绝对值)下降—过渡—随着距离增加而增加.当H/W约为1时，液桥侧面弯月面发生从凹到凸的过渡，平均曲率从负值到正值的转变，同时扎钉角从小于90°变成大于90°的过渡，FL从吸引力变为排斥力.大约在H/W=1.45时，FL达到最大值.随着H/W增加，FT绝对值慢慢减小，但是力始终为负值，为吸引力.因为FT是表面张力在垂直方向的投影，它的作用是将固体表面移近减少液气界面的面积，从而减小表面自由能.总体来说，当H增加时，FL从负值变成正值，FL从吸引力变为排斥力.但是在相同的H/W处，FT项在数量级始终超过FL分量，它起主要作用，所以总的毛细力始终是吸引力.如果H/W继续增加，当液桥的颈部变为最窄后，液桥不能再承受任何形式的拉伸，最后液桥断裂.

图3(b)结果表明，毛细力与接触角的大小有着密切的关系，毛细力随接触角的减小而增大，随H/W的增大而减小.θ越大，液桥两端液面的曲率rd越大，从而式(6)中ΔP的数值(绝对值)越小，因此毛细力越小.

4 讨论

本文计算得到的液桥形貌变化规律与经典液桥模型得到的规律不尽相同.主要表现为狭缝间液桥随着间距变化变得“越短越胖”，扎钉角随着高度增加而增大.而典型(不受限空间)两球形模型或者两平面模型之间的液桥形态变化是从凸变为凹或者凹形逐渐变细，即填充角随着高度的增加而减小.当间距到达临界高度之后，液桥最终断裂.出现不同现象的原因有4个：1)两狭缝之间的空间为受限空间，受限空间内的液桥的宽度阻止了三相接触线沿桥的宽度方向扩展，这点与两圆柱形纤维间液桥的形貌变化规律相似[23].而不受限空间中液桥可以向四周拓展[24-25],这也是受限空间液桥规律与不受限空间中液桥规律的最大不同点.2)本文计算中间距的数值远没有达到断裂高度，没有涉及临界断裂高度和液桥破裂能的计算，而大部分文献中研究的是接近断裂高度的液桥变化规律.3)本文研究的液桥体积较大，为毫升数量级，而大部分文献中，例如Swain等[26]研究的是小体积液桥，微纳米量级.当小体积的液桥高度接近断裂距离时，因为其表面(最细的“颈部”处)的自由能变小，出现断裂.4)大部分文献中，例如Valencia等[17]研究的是接触角为0的液桥，当两个表面之间的润湿液体可自由调整但不能自由平移的时候，小体积液桥形态为“anvil-like”形状，与本文中讨论的大体积液桥不同.Yaneva等[27]研究的是大接触角(θ=73°)和小体积(V/W3=0.65)接近临界断裂点的高度下的液桥，因此出现了填充角随着高度的增加而减小的现象.

5 结语

关注受限的水平狭缝中的液桥的三维形貌，使用椭圆近似方法计算液桥的体积以及分析参数对体积的影响.具体为建立了液体在水平狭缝内的外观轮廓的理论模型，采用椭圆弧假定推导出液桥体积和毛细力的计算公式.分析轴对称液桥形貌特征参数受到液体体积、间距、接触角和宽度等诸多因素的影响规律.将计算结果与实验结果和有限元软件模拟的结果相比较，吻合结果良好,说明该模型能较好地预测和描述液桥形貌及其轮廓特征参数.此外,计算结果表明毛细力随着高度宽度比的增大而减小之后趋于平缓.总的来说，虽然拉普拉斯力随着高度宽度比的增加，从吸引力变化为排斥力，但液桥内部仍以表面张力为主，所以总的毛细引力为吸引力.受限狭缝内的液桥随着间距的增加由凹变凸，即液桥逐渐变短变胖，这与不受限空间的液桥形貌变化大不相同.

本文模型为流体静力平衡中的液桥，也可用于探索液体对颗粒材料结构由干化-湿化的水力-力学耦合作用的细观机理和孔隙流体的液桥效应.但是理想模型没有考虑到液桥不对称、平面的粗糙度、液体重力因素等影响，使得模型及计算方法仍具有可开发性.后面将考虑更加复杂的不规则平面之间液桥问题以及液桥断裂的动态过程，以期能更深入了解狭缝中液体的形貌和受力状态.