三区复合型Tschebycheff方程边值问题的相似构造法
2023-01-30郑鹏社李顺初桂钦民
郑鹏社,杨 雨,李顺初,桂钦民
(1.西华大学 理学院,四川 成都 610039;2.北京东润科石油技术股份有限公司,北京 100029)
2010年,李顺初[1]在求解一类二阶常微分方程边值问题时,提出了利用具有相似结构的表达式来构造边值问题的解的办法——相似构造法.之后,一些研究者不仅将此方法应用于求解其他一维[2-4]二阶常微分方程边值问题,还利用其求解复合型[5-8]、三区复合型和n区复合型[9-10]常微分方程边值问题.在最新的研究中,何签等[11]和李顺初等[12]利用相似构造法,对三区复合型第一、二类Weber方程边值问题进行求解,此求解过程表明相似构造法是求解三区复合型微分方程边值问题的一种高效、准确的方法.相似构造法的应用为求解多种类微分方程边值问题提供了一种新的思路.
有关Tschebycheff方程边值问题的研究中,研究者们[13-14]讨论了一维和复合型Tschebycheff方程边值问题的解,基于以上研究成果,本文针对如下的三区复合型Tschebycheff方程边值问题进行研究:
(1)
其中:D,E,F,G,H,a,b,c,d,α1,α2,β1,β2为常数;ni(i=1,2,3)为正整数;α1,α2,β1,β2≠0,G2+H2≠0,D≠0;0 yi=AiTni(x)+BiUni(x), (2) 其中:Ai,Bi为任意常数,Tni(x)为Tschebycheff多项式,Uni(x)为第二类Tschebycheff函数. 引理2[14]关于二元函数 (3) 有: (4) (5) (6) 其中:i=1代表内区(a 证明依据Tschebycheff多项式Tni(x)和第二类Tschebycheff函数Uni(x)的递推公式[15] 同理,可以证明式(4)和式(6). 定理1若边值问题有唯一解,则其内区(a (7) 中区(b (8) 外区(c (9) 其中:Φ1(x)称作内区相似核函数 (10) Φ2(x)称作中区相似核函数 (11) Φ3(x)称作外区相似核函数 (12) yi=AiTni(x)+BiUni(x),(i=1,2,3), (13) 由递推公式,可计算出yi(x)的一阶导数,即 (14) (15) 将式(13)和式(14)代入两组衔接性条件中,能够分别得到: A1Tn1(b)+B1Un1(b)-A2α1Tn2(b)-B2α1Un2(b)=0, (16) A1n1[Tn1-1(b)-bTn1(b)]+B1n1[Un1-1(b)-bUn1(b)]- A2α2n2[Tn2-1(b)-bTn2(b)]-B2α2n2[Un2-1(b)-bUn2(b)]=0, (17) A2Tn2(c)+B2Un2(c)-A3β1Tn3(c)-B3β1Un3(c)=0, (18) A2n2[Tn2-1(c)-cTn2(c)]+B2n2[Un2-1(c)-cUn2(c)]- A3β2n3[Tn3-1(c)-cTn3(c)]-B3β2n3[Un3-1(c)-cUn3(c)]=0, (19) (20) 依据式(15)~(20)和式(3)~(6),能够得到关于待定系数A1,B1,A2,B2,A3,B3的系数行列式为 (21) 因为边值问题(1)的解是存在且唯一的,所以Δ≠0.根据Gramer法则,可以计算出待定系数A1、B1、A2、B2、A3、B3的值,分别为: (22) (23) (24) (25) (26) (27) 将式(22)~(27)代入Tschebycheff方程的通解(13)中,再结合式(10)~(12)和式(3)~(6)进行化简组装,可以得到三区复合型Tschebycheff方程边值问题(1)的内区解(7)、中区解(8)和外区解(9). 推论1对于三区复合型Tschebycheff方程边值问题(1),若内边界条件y1|x=a=1,则边值问题(1)的内区解为 y1=Φ1(x),(a (28) 推论2对于三区复合型Tschebycheff方程边值问题(1),若外边界条件y3|x=d=0(G≠0,H=0),则外区相似核函数为 (29) (30) 推论4对于三区复合型Tschebycheff方程边值问题(1),有 (31) 由上述求解过程可以归纳出求解三区复合型Tschebycheff方程边值问题(1)的相似构造法,步骤如下: 2)内区、中区、外区相似核函数的构造.外区相似核函数Φ3(x)由外区引解函数和外边界条件中的系数G,H组合构成,中区相似核函数Φ2(x)由中区引解函数、第二组衔接性条件中的系数β1,β2和Φ3(c)组合构成,内区相似核函数Φ1(x)由内区引解函数、第一组衔接性条件中的系数α1,α2和Φ2(b)组合构成,依据上述构造,可以得到式(10)~(12). 3)得出三区复合型Tschebycheff方程边值问题(1)的内区、中区、外区解.内区解由内边界条件的系数D、E、F、内区相似核函数Φ1(x)和Φ1(a)组合得出;中区解由部分内区解、衔接性条件中的系数α1、α2、内区引解函数、中区相似核函数Φ2(x)和Φ2(b)组合得出;外区解由部分中区解、衔接性条件中的系数β1、β2、中区引解函数、外区相似核函数Φ3(x)和Φ3(c)组合得出,基于上述组合,可以得到式(7)~(9). 求解如下的边值问题(a=1,b=2,c=3,d=4,n1=1,n2=2,n3=3,α1=1,β1=1,α2=2,β2=2,D=1,E=1,F=2,G=1,H=2): (32) 第一步:由定解方程(1-x2)y″1-xy′1+y1=0的两个线性无关解T1(x)和U1(x),构造边值问题(32)的内区引解函数 第二步:内区、中区、外区相似核函数的构造.依据式(12),构造出外区相似核函数 并计算 依据式(11),构造出中区相似核函数 并计算 依据式(10),构造出内区相似核函数 并计算 第三步:求解边值问题(32)的内区、中区、外区解.依据式(7),可以得到边值问题(32)的内区(1 依据式(8),可以得到边值问题(32)的中区(2 依据式(9),可以得到边值问题(32)的外区(3 (33) 1)在探讨三区复合型Tschebycheff方程边值问题(1)时,一方面,发现其内区、中区、外区解在结构上具有相似性,解的结构由内外边界条件和衔接性条件的系数、引解函数和相似核函数组装得到;另一方面,解的部分内容相同,其相同部分由内边界条件系数和Φ1(a)构成,且呈连分式结构形式. 2)在求解三区复合型Tschebycheff方程边值问题(1)时,发现二元引解函数总是由定解方程中的线性无关解来加以构造,内区、中区、外区相似核函数的系数只与内边界条件和衔接性条件的系数有关. 3)应用相似构造法求解三区复合型Tschebycheff方程边值问题时,可以发现相似构造法能够大大降低求解的难度,提高计算的速度和准确度.1 预备知识
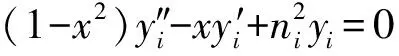
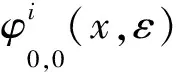
2 主要定理及证明

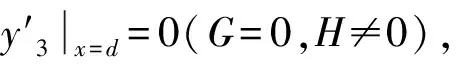
3 相似构造法的步骤
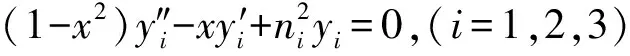
4 应用举例
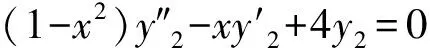

5 结论
