有机污染物色度降解动力学常数的神经网络研究

堵锡华，吴 琼，李 靖，陈 艳，田 林

(徐州工程学院 材料与化学工程学院，江苏 徐州 221018)

高级氧化技术(Advanced oxidation process，AOPs)是一种依托于声、光、电、磁等现代科技手段，生成具有极强氧化性带电离子或者自由基降解污染物的技术[1]，是处理难降解有机污染废水比较有应用前景的方法之一[2]，所以在污水处理技术的应用和发展研究方面受到越来越多科研工作者的关注[3-7].

近年来，定量构效关系(QSAR)研究在农药毒性[8]、环境污染[9]、医药[10-11]等领域得到越来越多的应用，利用人工神经网络(Artificial neural network，ANN)与定量构效，应用在化学[12]、药学[13]、环境科学[14]、土壤学[15]、食品科学[16]、农学[17]等众多领域.本文采用神经网络方法构建20种有机污染物降解速率的定量构效关系预测模型[18-20]，分析了对有机污染物降解速率的主要影响因素，为有机污染化合物的降解处理提供理论依据.

1 有机污染化合物及数据来源

20种有机污染物分子及降解速率(以色度降解动力学常数Kcolor表示)来源于文献[20]，降解动力学常数Kcolor根据公式ln(A0/At)=Kcolort计算得到.式中：A0为反应开始时的吸光度，At为反应时间为t时的吸光度，t为反应时间(min).Kcolor值见表1.文献采用的实验条件为：T=298 K、pH=4、使用λ=254 nm紫外光和过量的H2O2.

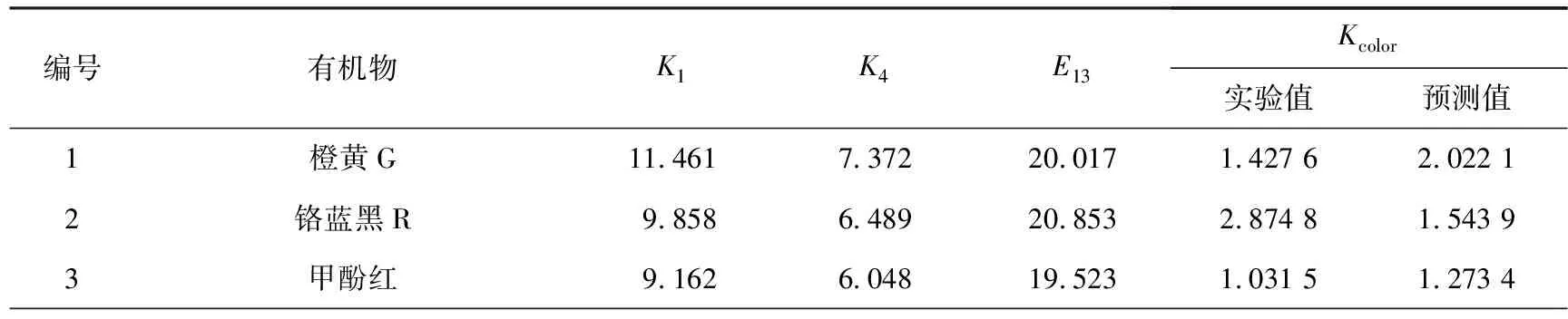
表1 有机污染物的色度降解动力学常数和结构参数

2 研究方法

2.1 形状指数和电性拓扑状态指数的计算和筛选

根据文献[20]中所列的20种有机污染化合物的分子结构，在MATLAB环境下采用文献[21-22]方法自编程序计算这20种分子的分子形状指数和电性拓扑状态指数，去除所得两类指数中全部或大部分指数值为0的数组，使用可进行统计分析、预测式分析、可视化分析和改进分析的MINITAB应用软件，对剩余数组和降解速率(以有机污染物的色度降解动力学常数Kcolor表示)进行最佳变量子集回归分析.按照样本数与变量数比值n/b≥5的要求[23]，优化筛选出形状指数K1和K4、电性拓扑状态指数E13共3个分子结构参数，相关结构参数见表1.这里采用二种不同种类的3个参数进行组合，是因为只是采用同一类的结构参数与Kcolor回归分析，所得方程的相关性不大理想；而采用多类参数分析，则又受到变量个数的限制，故经反复比较分析，发现当取形状指数K1和K4与电性拓扑状态指数E13这3个参数结合作为自变量时，与有机污染物的色度降解动力学常数Kcolor的相关性相对而言能达到最佳，最佳变量子集回归分析结果见表2.

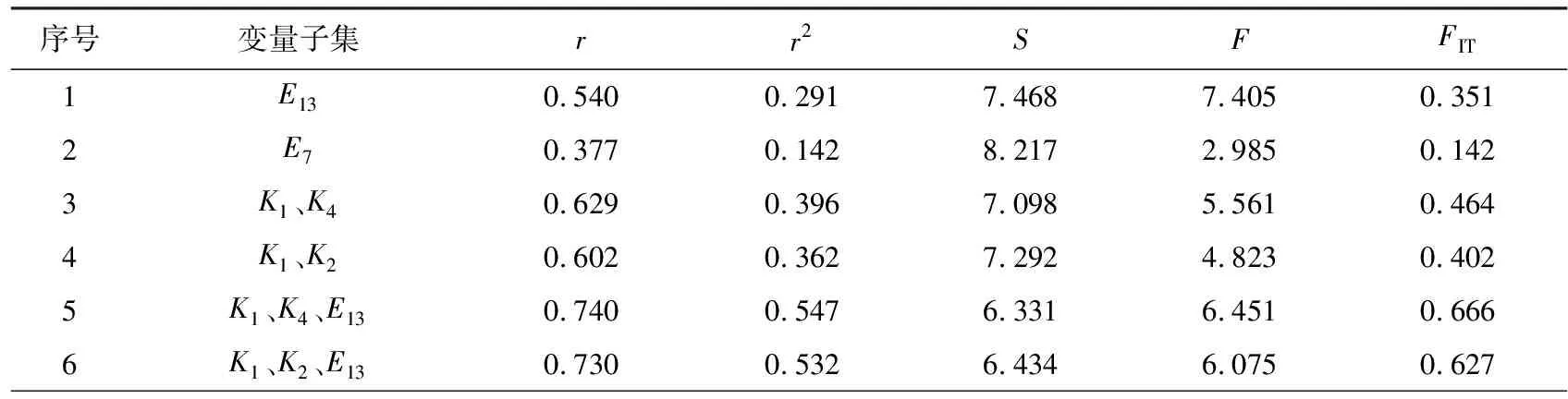
表2 分子形状指数、电性拓扑状态指数与Kcolor的最佳变量子集回归结果

分子形状指数K1和K4中的K1为1阶形状特征参数，反映分子的环性；K4=K1×K2，其中的K2为2阶形状特征参数，反映原子空间密度；E13则代表—OH、—O—基团片段.

2.2 多元回归模型的构建

考察文献[20]中所列的20种有机污染化合物的色度降解动力学常数Kcolor，与优化筛选出的分子形状指数和电性拓扑状态指数中的K1、K4和E13进行多元回归分析，得到多元回归模型为

Kcolor= 5.321K1-6.615K4+0.325E13-11.481，

(1)

n=20，r=0.740，r2=0.547，S=6.331，F=6.451.

模型(1)中n为回归分析样本数.该多元回归模型的决定系数r2只有0.547，相关性不好，说明结构参数与这些有机污染物的色度降解动力学常数之间不是简单的线性关系，需要进一步采用非线性研究方法进行研究.

2.3 神经网络法模型的构建

由于采用多元回归分析结构参数与色度降解动力学常数的线性方程不理想，为此以选择的3个结构参数作为神经网络的输入层节点，以色度降解动力学常数作为神经网络输出层节点，隐含层节点数则按照Andreao 等[24]和许禄等[25]建议规则：2.2>n/[(Si+2)Y+1]≥1.4.这里n为样本总数，Si为神经网络的输入层节点数，可以得到隐含层节点数Y的值，经过计算隐含层节点数Y应取2，故使用神经网络法研究的网络结构采用3-2-1方式.为防止神经网络建模过程中过拟合，将20种有机污染物分子随机分为3个组集：取每5种分子的第1、3、4种分子为训练集、第2种分子为测试集、第5种分子为验证集；计算所得结果较为理想.将本法建立模型得到的预测值列入表1中.

3 结果与讨论

经神经网络计算分析，得到预测有机污染化合物色度降解动力学常数模型的总相关系数R总=0.997 6，训练集R训练=0.966 5、测试集R测试=0.998 9、验证集R验证=0.995 6，无论是从总的相关系数还是3个组集的相关系数都可以看出，用神经网络法所得非线性模型的总相关系数，比多元回归法所得线性模型的相关系数提升较为明显，达到0.99以上，属于优级相关，利用构建的模型进行预测的色度降解动力学常数与实验值的吻合度较好(见图1)，明显优于多元回归法的吻合度(见图2)，说明分子结构参数与色度降解动力学常数之间存在非线性关系，本法建构的预测模型有良好的预测能力.

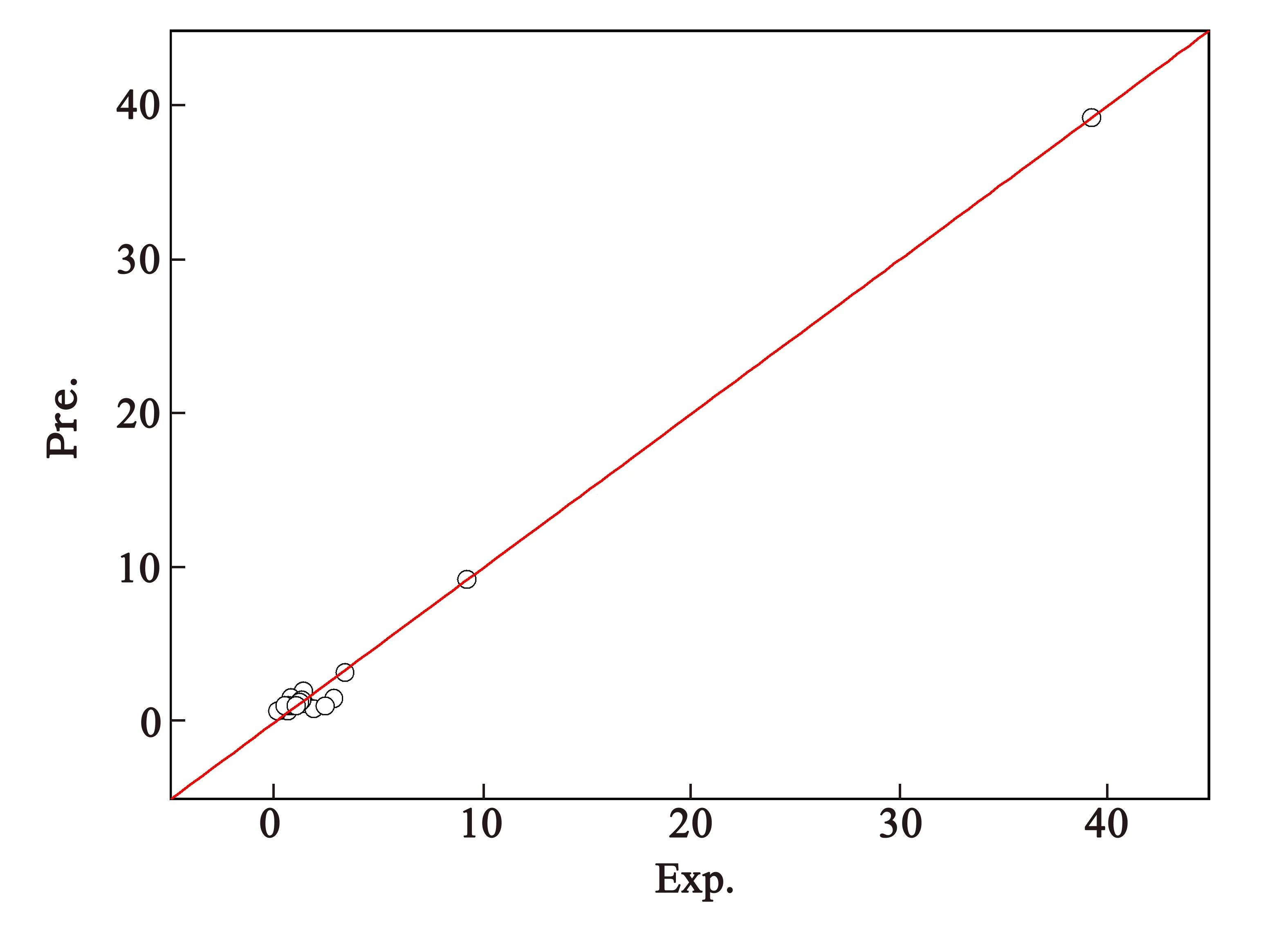
图1 神经网络法Kcolor的实验值与预测值关系

图2 多元回归法Kcolor的实验值与预测值关系

从图1可以看到，神经网络法预测值与实验值的对应点完全贴近对应值直线，而从图2看到，多元回归法预测值与实验值的对应点偏离完全对应值直线，有的甚至偏离较远.这里再以神经网络法模型所得预测值与实验值的误差作控制图(见图3)及雷达图(见图4)也可以看出，本法所得误差在可控范围内，说明所得结果较为可靠.

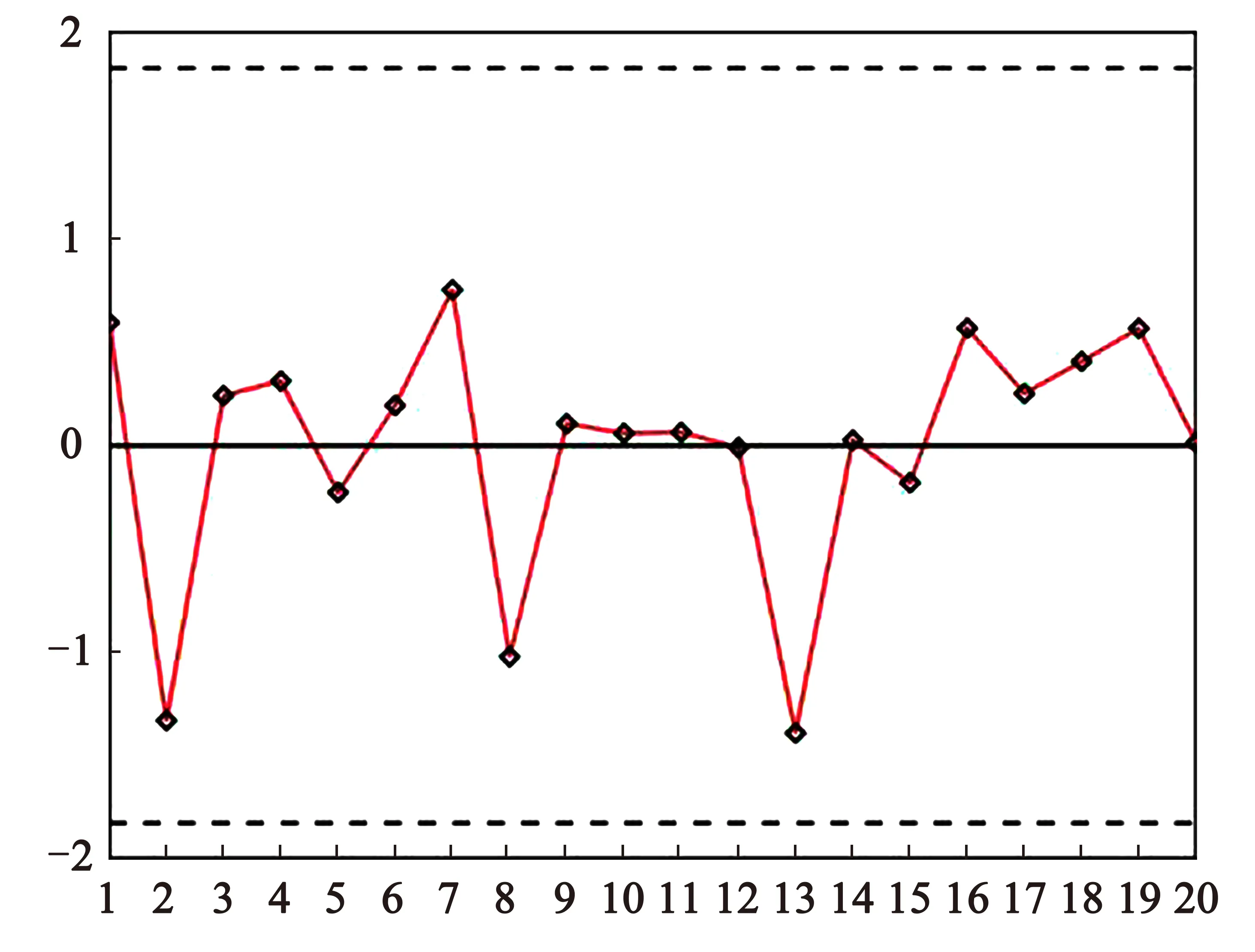
图3 Kcolor误差控制图

图4 Kcolor误差雷达图

考察这20种有机化合物分子的分子结构与其色度降解动力学常数的大小可以看出，当分子中含有的羟基、硝基等基团数越多时，有机物发生氧化反应的活性位点越多，在酸性条件下，被氧化降解的速率越大；当具有相同取代基及数目时，基团连接的位置则影响降解速率的大小；分子形状指数蕴含了分子的环性和分子中原子空间密度的特性，电性拓扑状态指数中的E13则能反映—OH、—O—基团片段在分子中的连接和电性特性，其值的大小与色度降解动力学常数的变化规律一致，故将其与神经网络法结合，可构建良好的预测模型[26-28].

为检验所建神经网络模型的应用能力，将该模型对茜素S、溴酚蓝、百里酚蓝、中性红、α-萘酚酞等有色化合物分子的色度降解动力学常数进行预测，所得结果除中性红是1.578 8外，其他几种有色化合物分子的色度降解动力学常数在6～16之间(相关数据也列入表1)，这说明在酸性条件下，对这5种有色化合物的色度降解能力较为理想，当然这需要通过具体的实验来进一步证实，但在理论上分析应该可靠.

由于有色化合物降解的色度降解动力学常数大小与多种因素有关，如所使用的降解催化剂、有色化合物的水溶性、温度、溶液的酸碱性等，均会对该值大小有影响[29-30]，本法只是对特定条件下的有色化合物降解速率有一定的预测作用，对其他条件下降解速率预测应用还是受到一定的限制，还需要更深入的研究.

4 结论

1)神经网络模型的相关系数明显优于多元回归模型的相关系数，说明优化筛选的分子形状指数、电性拓扑状态指数与有机污染化合物的色度降解动力学常数有良好的非线性关系，神经网络模型具有良好的稳定性和较强的预测能力，预测值与实验值吻合度较好.

2)神经网络模型具有一定的应用性，可判断其他化合物分子被氧化降解的能力.

3)影响有机污染化合物色度降解动力学常数的因素除分子的空间结构特性外，还有如—OH、—O—等基团片段是其主要影响因素.