借助几何直观构建数学模型——基于核心素养下的《乘法分配律》教学

李丽丽

（广饶县第二实验小学 山东东营 257300）

一、知识内容分析

教材呈现了分开算和合起来算两种不同的解题思路，列出结果相等的算式，让学生经历“感知建模一类比归纳一验证模型—质疑猜想一拓展认识”的建模过程。要求学生的思维已经开始由具体形象思维向抽象思维过渡，具备了一定的自主探究、迁移运用和推理能力。在探索加法运算律及乘法交换律和结合律时，学生已经经历了“猜想—验证—总结”这样的探究学习过程。因此，教学过程中要尊重学生已有的知识与经验，通过引导学生独立探究、归纳概括，自主总结出乘法分配律，建立模型[1]。

二、学科德育渗透点分析

2022版小学数学课程标准中提出，应使学生通过数学学习，形成和发展面向未来社会和个人发展所需要的核心素养。史宁中教授概括出以下三句话：用数学的眼光观察现实世界，用数学的思维分析现实世界，用数学的语言表达现实世界。这里可以将其归纳为三种基本思想：抽象、推理和模型。那我们借《乘法分配律》一课来谈一谈如何在代数的教学中引入几何模型支撑，让抽象变得“看得见”。几何直观主要是指利用图形描述和分析问题，将数学问题转化为直观的图，能具体生动地理解问题，符合学生的思维特点[2]。在许多情况下，借助几何直观可以把复杂的问题变得简明、形象。几何直观分为三个层次：感知、理解和洞察。受小学生思维特点的限制，本文主要涵盖感知、理解两个层次。

三、教学实施过程

1.创设情境，初感规律

师：同学们，在老师的校园里有一个漂亮的小花园，我们一起去看看花园里有些什么花吧！

课件出示情境图。

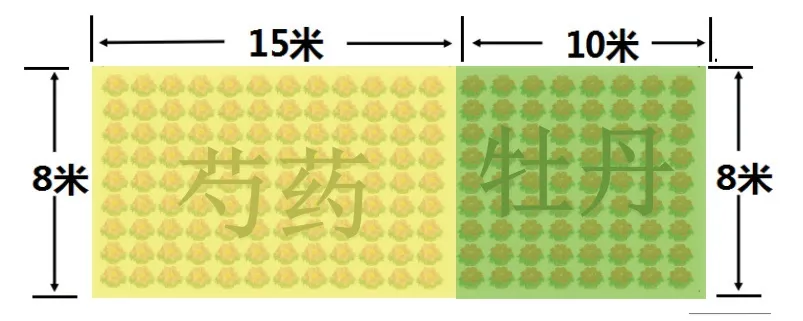
课件出示情境图。

师：请同学们仔细观察，你发现了哪些数学信息？

信息预设：芍药每行12棵，有9行。牡丹每行8棵，有9行。

学生回答，教师适时评价。

问：根据这些数学信息谁能提出数学问题？

生预设：芍药和牡丹各有多少棵？芍药和牡丹一共多少棵？芍药比牡丹多多少棵？

教师根据学生的回答，课件出示本节课要解决的问题：芍药和牡丹一共多少棵？

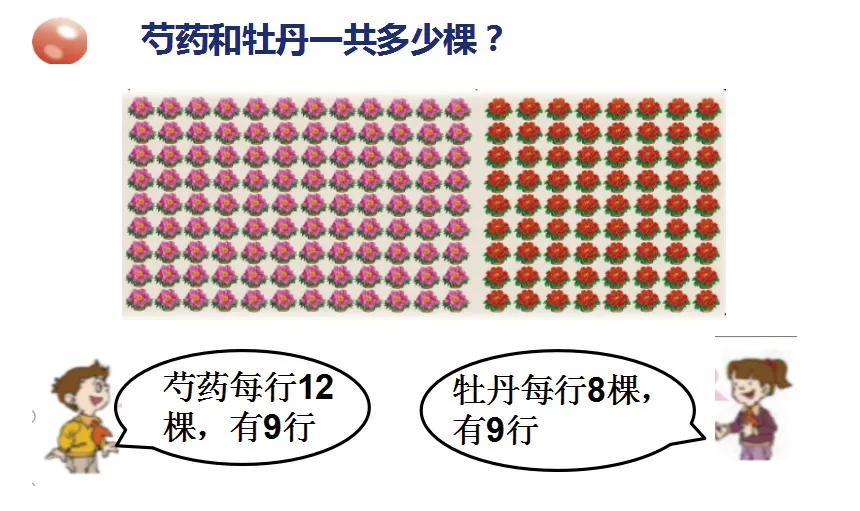
师：老师这里还有一部分关于芍药园和牡丹园的信息。

课件出示：芍药园长15米，牡丹园长10米，宽都是8米。

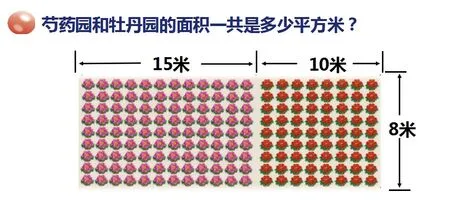
问：根据这些数学信息还能提出什么数学问题？

教师根据学生的回答，课件出示本节课要解决的另一个问题：芍药园和牡丹园的面积一共多少平方米？

学生独立思考解决以上2个问题，尝试列出综合算式。

交流汇报：学生投影展示做题情况，并结合情境图，说说算式每一步的含义。

师：我们刚才用了两种不同的方法解决了同一个问题，计算结果相等，所以可以用什么符号把这两个算式连接起来？（等号）

师板书等式：（12+8）×9=12×9+8×9

衔接：我们再来看下一个问题。

交流汇报：学生投影展示做题情况，并结合情境图，说说算式每一步的含义。

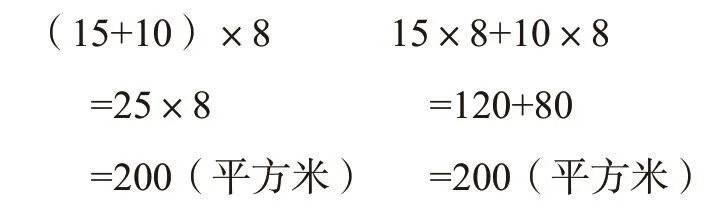
师：同样，这两个算式之间也可以画上？（等号）

师板书等式：（15+10）×8=15×8+10×8

【设计意图：学生通过自主解决教师创设情境中的实际问题，初步感知乘法分配律在生活中并不陌生，在解决问题过程利用数形结合，让学生对于分开算和合着算的理解简单明了[3]。然后学生通过观察、比较发现两组算式具有共同特征。从而初步感悟模型。】

2.对比观察，形成猜想，举例验证

（12+8）×9=12×9+8×9

（15+10）×8=15×8+10×8

师：观察这两组算式等号左右两边的式子有什么相同点和不同点？再看每组算式的左右两边之间有怎样的关系？这两组算式左右两边相等是巧合呢？还是有规律呢？同学们想不想来验证？

课件出示：仿照黑板上两组算式的样子，再写出一组这样的算式，然后计算你写的算式左右是不是相等？

学生上台板书自己写的算式，并说明自己的验证结果。教师借机向学生介绍一种巧妙的验证方法，即从乘法的意义角度来验证。

有没有同学能举出一个反例来推倒这个猜想呢（寻找反例和解释反例）？

【设计意图：在发现以上两组算式的规律特征后，引导学生猜想是否具有这些特征的一组算式都相等？学生在尝试举例中，进行验证发现结果都相等，从而进一步帮助孩子进行建模[4]。】

3.总结规律

看来这几组算式不是一个巧合，具有一定的规律。这个规律就是今天我们所要学习的乘法分配律（引出课题：乘法分配律）。

问：谁能根据上面这几组等式说一说什么是乘法分配律？

根据学生发言总结归纳乘法分配律。

问：如果我们用a和b代表这两个加数，用c代表一个数，那么乘法分配律用字母怎么表示呢？

生：（a+b）×c=a×c+b×c 师板书

【设计意图：学生根据之前学习交换律和结合律的经验，自然而然就想到可以用字母来表示乘法分配律[5]。】

4.运用规律

衔接：接下来，让我们用学过的知识来解决2个问题，有信心吗？

（1）在方框里填上适当的数。

（1）（100+2）×12=100×_______+2×___

（2）236×3+236×7=236×（_______+_______）

我们前面学习了乘法结合律和交换律可以使计算简便，那么乘法分配律能否使计算简便呢？

比较第1题中的2组算式，看哪个计算简便，为什么？

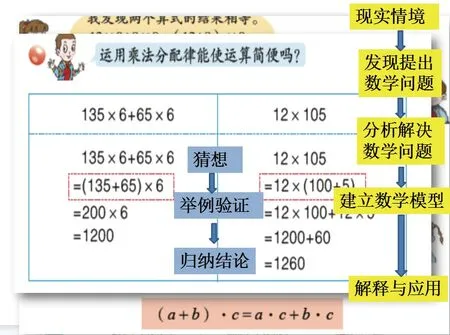
（2）计算 135×6+65×6 12×105

汇报交流并总结。

【设计意图：在应用中内化规律，建立模型。这里设计的练习题既依据教材又高于教材，在第一题的基础上渗透应用分配律可以使计算简便的意识，思考所学规律的价值，为之后简便计算的学习做铺垫。】

5.总结反思

问：这节课你有哪些收获？

师小结：这节课我们通过观察猜测，举例验证，归纳总结，最后应用规律来认识了乘法分配律。我们可以运用这种方法来探究更多的新知识，希望同学们在以后的学习中多观察、多思考，做一个勇于探索、敢于挑战的好孩子！

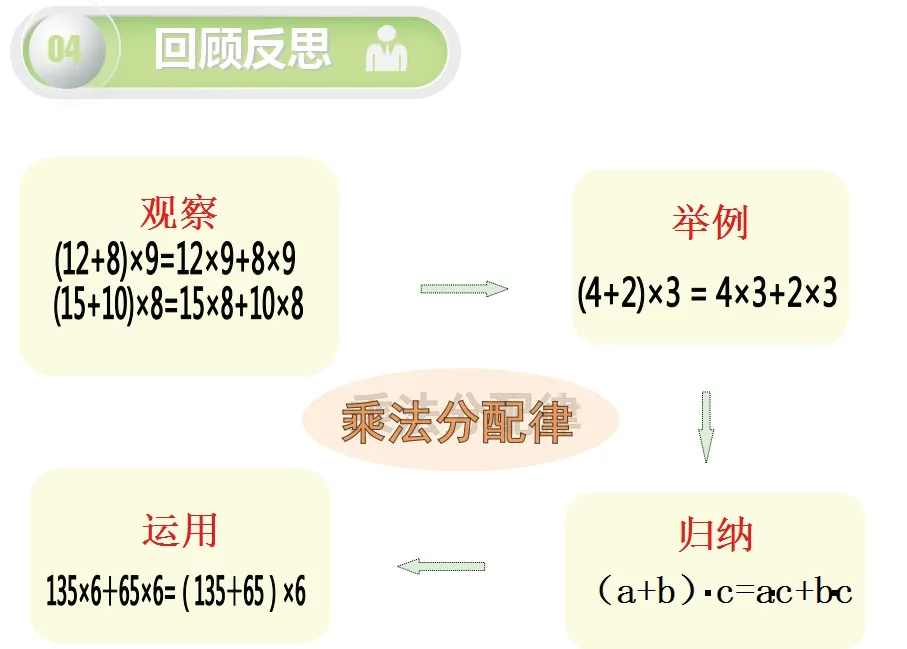
【设计意图：总结回顾不仅回顾这节课所学的知识，还要回顾学习知识的过程，即对建模过程的梳理，帮助学生形成整体的思维。】

四、教学总评

1.几何直观匹配问题情境

在本节课中虽然是通过观察算式来发现规律，但是在算式形成的过程中为孩子们提供直观、形象的现实情境图，让孩子在理解算式所表示的实际意义的基础上，来更好地比较所谓分开算和合起来算其实本质相同。问题情境通过几何直观的形式呈现，让学生在形中提升对数的认识，从而为建立模型打好基础。

2.经历建模的过程

大部分同学通过计算很容易得出分开算和合着算结果相等，从而把两边用等号连接，但是很少有学生能想到运用乘法的意义来解释为什么相等，这也反映出在之前的学习中我们更加关注的是学习的结果而不是过程。这就需要教师在之后的教学中充分发挥引导作用，促进学生提高学习效率。

3.发展模型意识的层次呈现

学习从模仿开始，学生在解决“牡丹和芍药一共有多少棵”和牡丹园和芍药园面积的过程中，初步感知了乘法分配律的结构特征，接下来，学生在老师引导下观察、比较这两组算式，进一步发现这些算式的特点，使乘法分配律的表象跃然于黑板上，同时也清晰地投射在学生的头脑中。在之后的仿写举例时，学生举出很多例子来验证是否符合乘法分配律，学生经历完有层次的探究过程后，总结出乘法分配律也就是顺理成章的事情，从而在内化运算规律的同时还发展了模型意识。