一致性视角下“数与代数”领域主题统整式教学探究——以“小数乘法”的教学为例

马丽丽

从表面上看，“小数乘法”的教学只要解决“积的小数点定位”问题就可以“一通百通”了。但基于“学”的视角细细思量，就会发现：小数乘法相较于整数乘法，虽然形式上只多了“一点”（小数点），但理解的难度可不止增加了“一点儿”。在学生的错例中，除了“整数乘法算错”“计算习惯不佳”等原因之外，还有几类错误引起了笔者的关注。其一，末尾有零。如在计算1.15×3.2、0.6×16.5这类题目时，由于按照整数乘法来算，算出的乘积末尾有零，学生在确定积的小数位数时，往往会分不清应该先点上小数点还是先划去乘积末尾的零，从而导致结果出错。其二，添零补足。如在计算0.28×0.28、0.045×1.4这类题目时，按照整数乘法算出的积位数不够，还原为小数时需要添零补足，这时学生往往会少添零或多添零。类似的错误还会出现在口算中，如学生常常会将0.03²、0.1²等算出0.09、0.1等错误答案。其三，乘加混淆。明明要算乘法，却将小数加减法的算法杂糅进来，如计算3.8×5.4，有学生先算十分位8×4＝32，十分位写2，向个位进3；再算3×5＝15，加上进上来的3，得18，所以得到的计算结果是18.2。学生出现这些错误并非偶然，主要是由于他们对运算意义的理解不清晰，对各类算理的理解不通透，且尚未在不同计算规则之间建立起联系。

由此看来，要想突破学生学习小数乘法的困难，就需要教师从一致性的视角对意义、算理、算法进行整体架构，既要沟通小数加法与小数乘法之间的联系，也要厘清乘法意义与算理算法之间的底层逻辑，还要对整数乘法、小数乘法与分数乘法之间的内在关联进行合理统整，这样才能引导学生实现真正意义上的“明算理、通算法”。

一、例谈一致性视角下“数与代数”领域的主题统整式教学

教师在教学中不能仅仅关注知识表面的一致性，更要基于学情，深入知识内核，把握知识内在结构、内容本质的一致性，从而引导学生突破学习难点，整体建构知识体系。那么，小数乘法的教学该如何统整、如何改进呢？下面，本文就以“小数乘小数”的教学为例，谈谈笔者的实践与探索。

1.层层推进明算理

课始，学生小组交流小研究的内容，教师巡视，请不同算法的学生上讲台板演。黑板上呈现出三种算法（如图1）。经过全班第一轮交流，学生已经可以借助积的变化规律判断出只有第三个竖式是正确的。

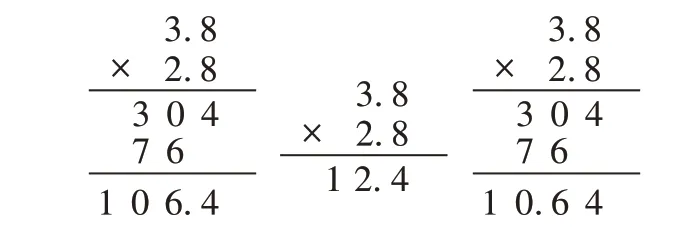
（图1）

师：前两个竖式究竟哪里出问题了？

生1（板演第一个竖式的学生）：其实，我的计算过程和第三个竖式是一样的，只是我把小数点的位置点错了，应该点在这里（指着0的右下角）。因为3.8和2.8都乘了10，积就会乘100，所以要把乘出来的积除以100，所以是10.64。

生2（板演第二个竖式的学生）：我算错了，我算的是八八六十四，写4进6，二三得六，再加进上来的6，所以算出了12.4。

生3：我想补充，他其实是先算0.8×0.8，再算2×3，最后把两部分结果加起来。

师：这样算，问题究竟出在哪里了呢？让我们结合题目画图来看一看，（边讲解边画出图2）我们计算的是小明房间的面积，整个房间是个长方形，它的长是3.8米，可以看成3米和0.8米，宽2.8米可以看成2米和0.8米。那么，0.8乘0.8算的是图中的哪个部分？2乘3算的又是哪个部分？

（图2）

生2：我明白了，这两个乘积加起来，只算了其中两部分的面积，和总面积相比还缺了两块面积。而且边长0.8米的正方形，面积不可能是6.4平方米，所以0.8×0.8＝0.64（平方米）。

师：刚才，我们通过数形结合找到了错误的原因，真好！既然我们认同这种算法，那大家能不能通过画图找到我们计算的根据呢？

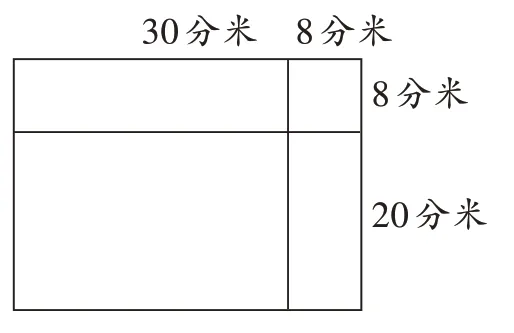
生4（边画出图3边解释）：竖式中的8×38=304，算的是上面长方形的面积；再算十位，20×38=760，求的是下面长方形的面积，合起来就是整个房间的面积。

（图3）

…………

2.多维求联通算法

（1）归纳：小数乘小数该怎样计算？

在对3.8×2.8的计算方法达成共识之后，让学生用同样的方法计算4.15×2.5，收集不同的算法（小数点对齐、末位对齐、将2.5的末尾添0变成2.50与4.15对齐），并投影展示、比较这些算法有什么相同点和不同点。在比相同点的时候，将落脚点放在计算过程、计算方法上；在比不同点的时候，重点关注列竖式时该如何对齐。

在学生就列竖式的对齐方式达成共识之后，组织他们归纳小数乘小数的计算方法，重点明确该如何确定积的小数点位置。

（2）沟通：与小数乘整数的算法有何联系？

师（出示图4）：小数乘小数和之前学习的小数乘整数在算法上有什么联系？你能用今天学习的知识来进一步解释2.35×3的积为什么是7.05吗（小数点为什么点在7的右下角）？

（图4）

二、一致性视角下“数与代数”领域主题统整式教学策略

1.以计数单位为基，达成数的认识的深度理解

学生的数学学习从来都不是突然感到困难的，执果索因，总能找到前面学习中埋下的“隐患”。从一致性的角度来看，算理的理解和算法的掌握最终都会归结为“数”，而无论是整数、分数还是小数，都需要从两个层面加以分析——计数的单位是什么？包含多少个这样的单位？聚焦意义理解，不能停留在学生从表面形式上认识小数，也不能满足于学生“背书”般地说出“一位小数表示十分之几，两位小数表示百分之几，三位小数表示千分之几……”。要让学生真正理解小数，教师就必须重视引导学生建构小数数位和计数单位，紧扣十进制单位的“细分”和“累加”，让学生既能从较大单位的不断细分层面理解小数的产生，又能从较小单位的逐渐累加层面来认识小数的组成，进而理解更多的小数。对小数意义的学习只有从形式模仿走向核心理解，才能在真正意义上夯实承重墙，才能为学生后续理解小数运算的算理打下坚实的基础。

2.以运算定律为媒，关联乘法意义的多重表达

在理解算理、探索算法之前，学生应当弄清楚“为什么用乘法算”，搞明白小数乘法表示的意义。小数乘法的运算意义，有的可以借助整数乘法来理解，比如0.8×3可以表示3个0.8相加；而像3.8×5.4这样的小数乘小数，就需要结合分数乘法的意义来理解了。但是，根据教材的编排顺序，学生是先学习小数乘法后学习分数乘法的，因而当下无法根据分数乘法的意义来解释。面对这样的“尴尬”，我们其实可以借助运算律来帮助学生关联小数乘法的多重意义表达，以弥补“小数乘整数”与“小数乘小数”的意义断层。比如，教师可以适当补充这样的情境：张叔叔每小时步行可以走3千米，他0.8小时可以走多少千米？学生可以根据“速度×时间=路程”的数量关系列式3×0.8，然后可以结合乘法分配律来解释，把3×0.8连续相加10次就等于3×8，所以3×0.8可以表示为“3×8的十分之一”；还可以结合乘法结合律——3×0.8＝3×（0.1×8）＝（3×0.1）×8，来理解3×0.8表示3的十分之一再乘8，即3×0.8可以表示为“3的十分之八”。像这样将小数乘法与运算律进行关联，不仅能丰富学生对小数乘法意义的理解，也能为后续进一步沟通整数乘法、小数乘法与分数乘法之间的联系埋下伏笔。

3.以几何直观为径，助推计算原理的逐层厘清

小数乘法是乘法意义的一次扩展，这本身就给教学带来了困难，再加上小数乘法运算依赖于分数乘法，如果不能提供有力的脚手架，学生就可能只是机械地记住了计算法则，被动地执行运算程序。由儿童的数学学习心理可知，越抽象的概念建立越需要直观形象来支撑，因此，借助几何直观来厘清算理是一个不错的方法。在上述案例中，教师发现学生不约而同地算出了“3.8×2.8＝12.4”这个结果。显然，用积的变化规律并不能很好地解释“12.4”错在了哪里。“理”不通，则“法”不顺，所以笔者呼应例题中的实际情境（求小明房间的面积），以形助数，从而实现了学生的真纠错、真理解。在图中，学生很清楚地指出了3.8×2.8＝12.4的错误所在，同时还利用这个图进一步验证了正确的算法。这样的数形结合，让原本说不清道不明的错误一下子变得显而易见、清晰明了；学生对算理的理解也更深入了一层；另外，到了中学阶段，这幅图还能帮助学生解决“（a+b）×（c+d）”的多项式乘法问题。

4.以对比辨析为途，实现计算法则的顺畅迁移

在学生的头脑中，不同计算方法往往是说不清，理还乱：小数加减法要相同数位对齐，小数乘法却要末位对齐；小数乘整数时，积的小数位数与乘数的小数位数相同；而小数乘小数时，积的小数位数是两个乘数的小数位数之和……这些零散又看似不同的知识给学生的理解和掌握带来了诸多困难，不利于他们从整体上建构知识。算法与算理是计算教学的一体两翼。在学生充分理解算理之后，教师还要关注算法的统整，引导学生站在更高位去归纳“通法”。通法的提炼既有利于学生将所学的计算模块化，也有利于新计算内容的迁移学习。在上述教学案例中，在学生学习“小数乘小数”的内容之后，教师再次出示“小数乘整数”例题图，引导学生比较思考两者在算法上的联系，使他们感悟到两者在算法上的一致性——都可以看作“乘数的小数位数之和，就是积的小数位数”，只不过由于将整数的小数位数看作“0”，所以才出现了“积的小数位数与乘数的小数位数相同”这种情况。不仅如此，等六年级学完分数乘法之后，教师还可以再次“回头看”，来一次“小数乘法的再探索”，有了分数乘法的加持，学生对小数乘法的理解会更加深刻，也会对整个乘法运算有一个更加完整、更加结构化的认识。

综上所述，一致性视角下的小学数学主题统整式教学为培养学生核心素养提供了新的视角和有效路径。它要求教师改变之前“一个例题接着一个例题散点教”的碎片化教学方式，破除“一道习题连着一道习题重复做”的机械式刷题现象，整体把握知识结构和内容本质，围绕知识群展开教学；同时，找准发力点，夯实承重墙，打通隔断墙，促进学生举一反三、触类旁通，推动他们的思维不断进阶，习得“带得走”的能力。