键合丝最小直流熔断电流的建模与分析
2023-01-28曹小鸽张艳肖
曹小鸽,张艳肖,杨 杨
(西安交通大学城市学院 电气与信息工程系a 物理教学部b,西安 710018)
近年来微电子产业及光纤通信产业发展迅速,键合丝作为微电子半导体封装及光纤通信用半导体器件封装的重要材料之一,用于芯片内部引线及芯片与外管脚的电气连接[1-4]。半导体封装要求键合丝要有高的可靠性[5-7]。针对键合丝的化学稳定性已经有一些文献做了研究[8-10]。对键合丝的熔断电流方面的研究,曹军[11]给出20.32 μm直径的高纯铜线和微合金铜线的熔断电流分别与时间及弧长的实验关系曲线,以及根据实验结果拟合出微合金铜线的熔断电流分别与时间及弧长的函数关系。范红等[12]给出不同直径下KT6型银合金丝熔断电流随着长度变化的实验曲线。黎学文等[13]给出25 μm线径3 mm长的键合金丝、金合金丝和银合金丝的实验熔断电流值。伍艺龙等[14]对小线径键合金丝熔断电流进行了测试。Heraeu公司给出10 mm长键合铜、金和铝丝随直径变化的实验熔断电流值和直径25 μm的键合铜、金和铝丝随长度变化的实验熔断电流值[15]。对于键合丝熔断电流理论计算方面,Raytheon公司给出10 mm长度的铜丝、金丝和铝硅丝的熔断电流与引线直径的线性关系的经验公式[6],但未说明具体环境对熔断电流值的影响。
本文首先在考虑键合丝工作环境的基础上进一步对其熔断电流做理论分析并建立键合丝最小直流熔断电流的理论计算模型。其次用COMSOL Multiphysics有限元软件建立键合丝直流工作时的电热耦合模型。最后用建立的理论及仿真模型分析不同直径及不同长度下的金、铜、银键合丝的最小直流熔断电流值。
1 理论模型的建立及计算公式的推导
1.1 键合丝最小直流熔断电流的稳态热传递模型
熔丝的电流越大熔断时间越短,电流越小熔断时间越长,当电流小到一定值时其熔断时间为无穷长,即不能熔断,这个电流被称为最小熔断电流,额定工作电流必须小于最小熔断电流[16]。影响键合丝最小熔断电流值的因素有很多,如:丝材质、丝长、丝横截面积、环境温度、热对流和热辐射的参数等[3]。图1表示长l的键合丝在最小直流熔断电流时的热传递及温度分布示意图。
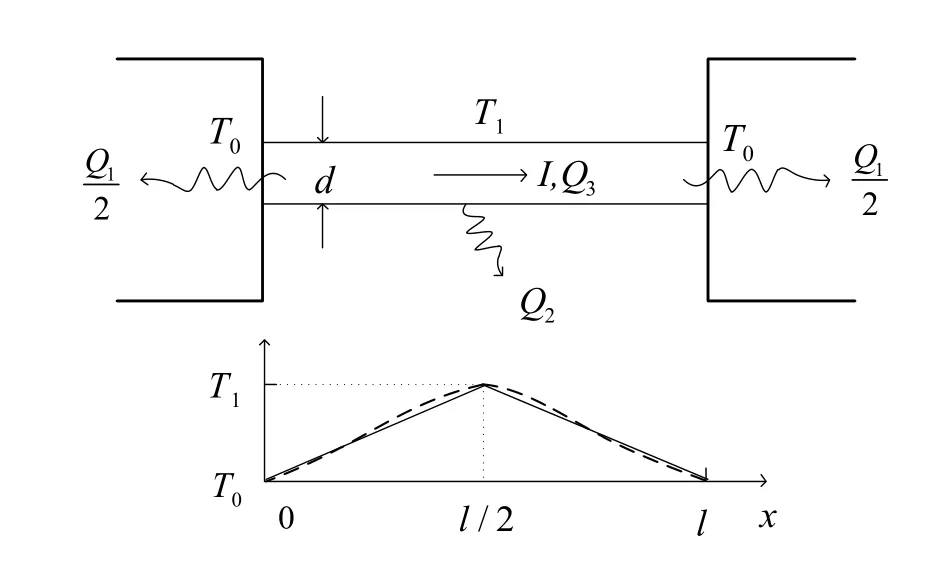
图1 键合丝最小直流熔断电流的稳态热传递及温度分布示意图Fig.1 Diagram of the steady-state heat transfer and temperature distribution of minimum DC fusing current of bonding wire
图1中,d为键合丝的直径,T0为外界环境温度,室温时为293K,T1为金属的熔点。单位时间内通过丝两端热传导出去的热量为Q1,单位时间内通过丝表面积向空气对流传导的热量为Q2,电源在单位时间内通过电流I向键合丝提供的热量为Q3。键合丝通过表面积热辐射的热量太小[3],理论建模时忽略不计。当d<<l时,可认为温度T是位置坐标x的函数,温度分布只随键合丝轴向变化,并不随径向变化,即同一x位置处温度相同。整根丝中间温度最高,为T1,两端温度最低,为T0,并且温度分布呈抛物线状对称分布[17],如图1中虚线所示。为了模型简化采用温度分布随轴线线性变化[18],如图1中穿过虚线的实线所示。
1.2 键合丝最小直流熔断电流的求解
根据傅里叶热传导定律[19]:

式中k为键合丝的热导率,A1为丝的横截面积,即πd2/4,负号表示热量总是从高温部分向低温部分传导。键合丝的温度随轴向x线性变化,则温度梯度:
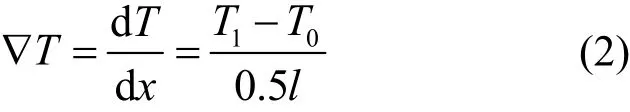
∇T对于材料及长度确定的任一键合丝可视为常数。考虑金属热导率随温度变化,由文献[20]给出的金属热导率随温度变化的实验数据可绘制出金属热导率和温度的关系图,如图2所示。
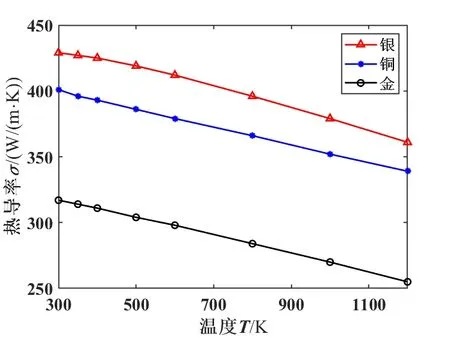
图2 几种金属热导率随温度变化关系图Fig.2 Temperature dependence of the thermal conductivity of several metals
从图2可见,金、银和铜这几种金属的热导率从室温T0到熔点T1几乎随温度呈线性变化。再由文献[21]给出金属的热导率的一些实验数据,可得这三种金属的热导率k从室温T0到熔点T1近似满足以下关系:式中k0为金属室温热导率,k1为金属熔点热导率。结合公式(1)至公式(3)可求出单位时间内通过丝两端热传导出去的热量:
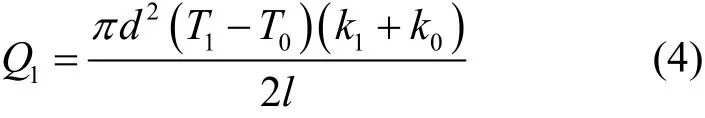
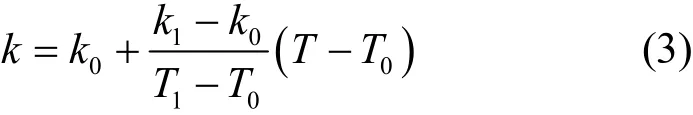
由公式(2),可得轴线任一x处的温度T满足:
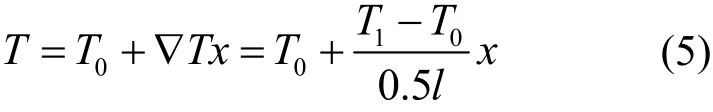
再根据热对流公式[19]:

式中α为空气对流系数,A2为物体与空气接触的表面积。可求得在单位时间内键合丝通过表面向空气传导出去的热量:
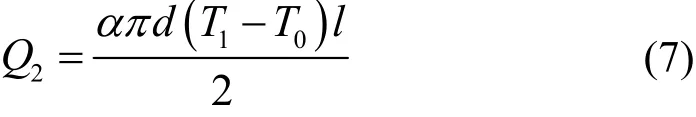
一般金属电导率σ与温度T存在如下关系:
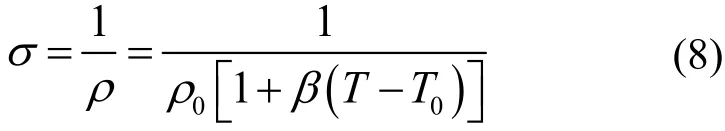
式中ρ0为室温293 K时金属的电阻率,β为金属的温度系数。可求得l长度的键合丝电阻:
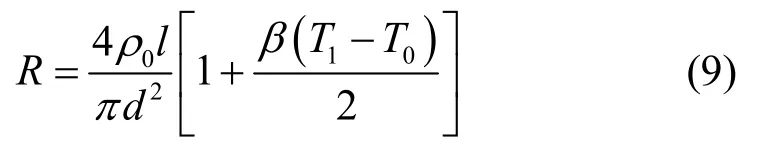
单位时间内电源通过电流I向键合丝提供的热量为:
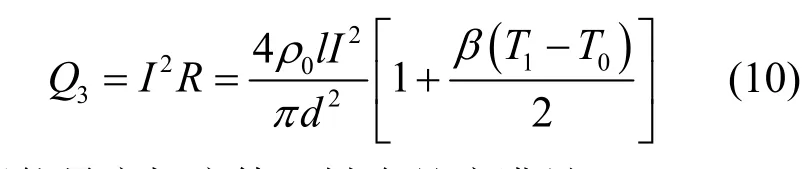
根据能量守恒定律,键合丝应满足:

将公式(4)、(7)及公式(10)代入公式(11),可得熔断电流:
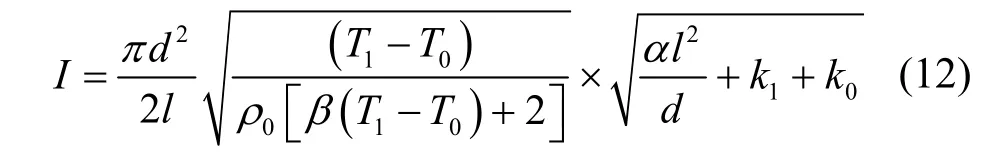
公式(12)即为所建立的考虑环境影响时的键合丝最小直流熔断电流的理论计算公式。当键合丝的材料特性参数、尺寸、对流系数确定后,即可利用公式(12)计算出键合丝室温下的最小直流熔断电流值。如果外界环境温度不为室温,将公式(12)中的T0改为相应环境温度值,相应的k0和ρ0改为该温度对应的热导率和电阻率后可计算其最小直流熔断电流值。并且从公式(12)还可以看出在材料及环境不变时,熔断电流值随着直径的增大而增大,随着长度的增大而减小。也应注意此公式应用有几个前提:1) 忽略键合丝热辐射的热量。2)d<<l,温度T不沿径向变化,只沿轴向线性变化。3) 金属的热导率从室温T0到熔点T1随温度线性变化。
表1为三种键合丝的物理参数值。但公式(12)还稍显复杂,为计算方便,再给出几种特殊情况下最小熔断电流的简易计算公式。

表1 三种键合丝的物理参数值Table 1 Parameters of several types of metals
1.3 键合丝最小直流熔断电流简易计算公式
1.3.1 工作环境密闭而导致对流系数α几乎为零时
当对流系数α几乎为零,即Q2忽略不计。只考虑键合丝从两端热传导出去的热量Q1时:
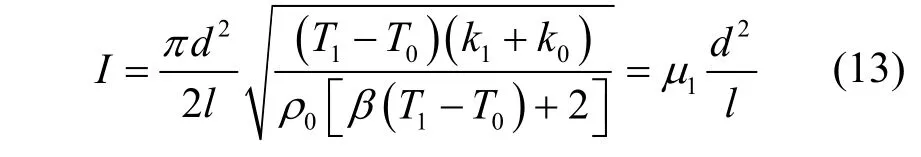
1.3.2 短丝、长丝最小直流熔断电流的计算
当键合丝产生的热量主要通过丝两端热传递出去时,即Q1>>Q2时,丝材为短丝;当键合丝产生的热量主要通过表面积热传递出去时,即Q1<<Q2时,丝材为长丝。当Q1=Q2时,根据公式(5)和公式(6)可求出长短丝临界长度短丝时,Q2可忽略,熔断电流:
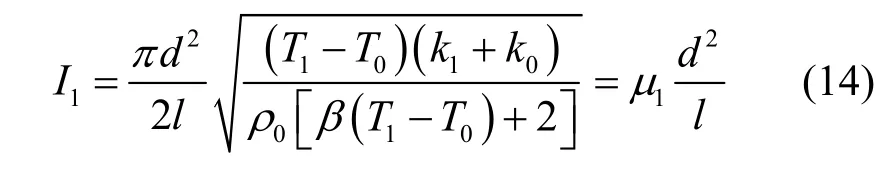
其结果与当对流系数α忽略不计时相同,μ1可称之为短丝系数。长丝时,Q1可忽略,熔断电流:
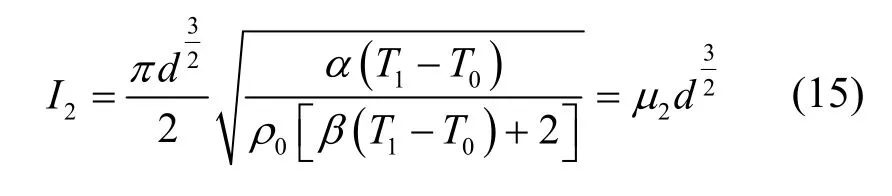
表2给出部分键合铜丝的l临、μ1和μ2的值。

表2 键合铜丝的长短丝系数及不同直径下的临界长度Tab.2 Long-wire and short-wire coefficients of the bonding copper wire and the critical length for different diameters
从表2可看出,短丝系数μ1跟材料有关系,材料确定为铜后,μ1的值不变。当材料确定后,μ2是对流系数α的函数,随着α值增大而增大。对流系数不变时,临界长度l临随着直径增大而增大;键合丝直径不变时,临界长度l临随着对流系数α值的增大而减小。
1.4 几种熔断电流计算公式对比
铜丝直径25 μm、对流系数α为50 W/(m2·K)时,计算出μ1=5.225×106A/m,μ2=1.125×106A/m3/2,进而根据公式(12)、(14)及(15)可计算出I、I1和I2,三者的关系如图3所示。
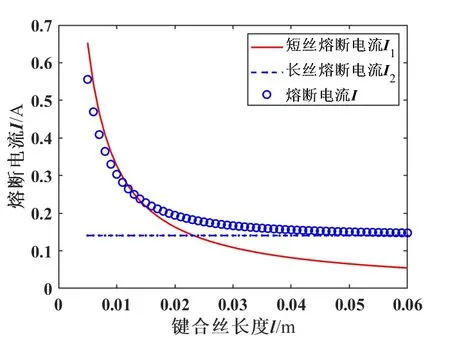
图3 长短丝熔断电流公式与总熔断公式对比Fig.3 Comparison of the short-wire, long-wire and the total fusing current formula
从图3中可明显看出,在丝较短的情况下短丝公式(14)与最小直流熔断电流I符合得比较好,在丝较长的情况下长丝公式(15)与I符合得比较好。故在判断键合丝为长丝或短丝后,可以用长丝或短丝公式简易计算键合丝最小直流熔断电流值。
2 仿真模型的建立及与理论计算模型对比分析
2.1 键合丝直流电热耦合仿真模型的建立与分析
使用多物理场有限元仿真软件COMSOL Multiphysics建立在一定环境下键合丝的直流电热耦合模型。键合丝设置为具有一定尺寸的长直圆柱体,材料可按照表1的值设置,外界环境温度及键合丝两端的温度可设置为室温293 K,设置对流系数及材料表面辐射率后,再通有电流激励后可仿真出键合丝的温度场分布。仿真模型可以改变键合丝的直径、长度以及键合丝的材料,也可以改变外界环境温度及空气对流系数等,这样可以仿真出考虑外界环境时不同材料及不同尺寸的键合丝熔断电流值及其温度场分布。
图4为金丝在2 mm长、直径为25 μm及对流系数α为50 W/(m2·K)时的室温下通一直流电流I为1.3362 A的温度分布图。从图4可以看到,金丝中间的温度达到熔点1337 K,该电流值即为此键合丝在该环境下的最小直流熔断电流值。图5为其沿轴向的仿真温度值及其数据拟合曲线与理论采用线性温度分布的对比图。拟合曲线呈抛物线状分布,拟合公式为:
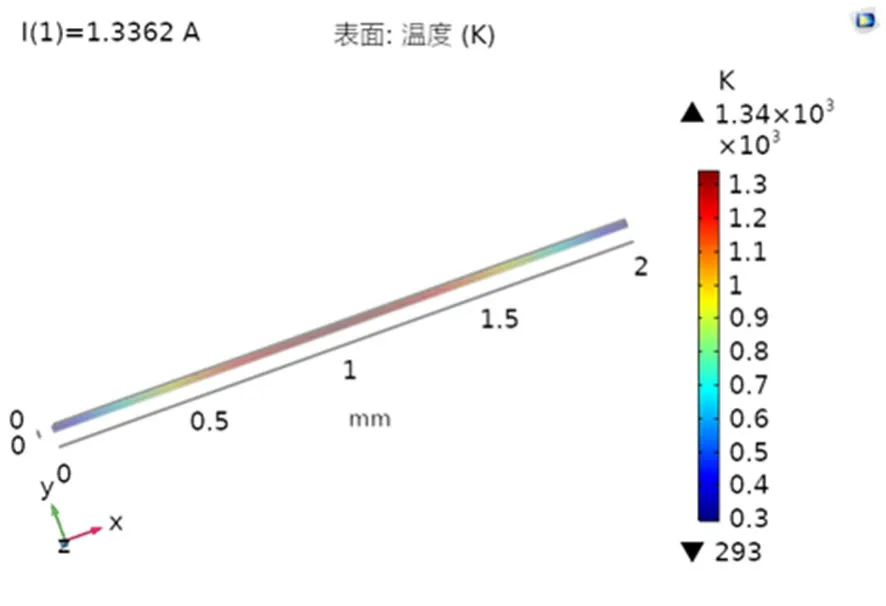
图4 金丝(Φ25 μm×2 mm)的温度分布仿真图Fig.4 Simulation diagram of the temperature distribution of gold wire (Φ25 μm×2 mm)
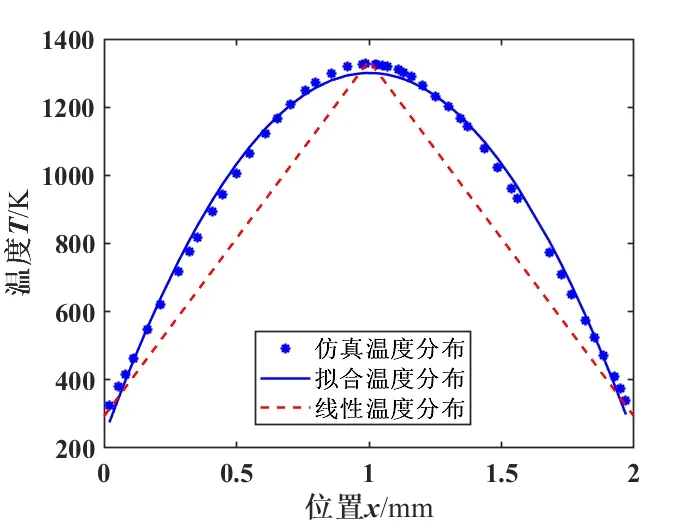
图5 金丝(Φ25 μm×2 mm)轴向温度分布对比Fig.5 Axial temperature distribution of gold wire (Φ25μm×2 mm)
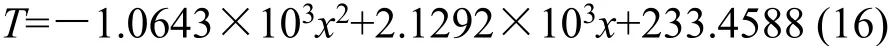
同时可计算出仿真得到的键合丝的温度平均值比按照线性化处理的键合丝的温度平均值高112.8 K。图6为该金丝在0.5 mm处的径向温度分布图,也呈抛物线状分布,但径向温差仅为0.001 K,故理论分析时若d<<l,径向温差的影响可忽略不计。当仿真不设置表面辐射后,仿真得到的最小直流熔断电流值为1.3358 A,与考虑表面辐射后的电流仿真值1.3362 A相对误差为0.03%,故理论分析时材料表面辐射的影响也可忽略不计。利用理论公式(12)计算出该键合丝的最小直流熔断电流为1.055 A,比仿真得到的电流值小,仿真值是理论值的1.27倍。综合以上分析,存在误差的主要原因是理论分析时温度的轴向分布按照线性化处理所造成。当金键合丝长度为5 mm时,理论计算的最小直流熔断电流值为0.4374 A,仿真值为0.54 A,仿真值是理论值的1.23倍。
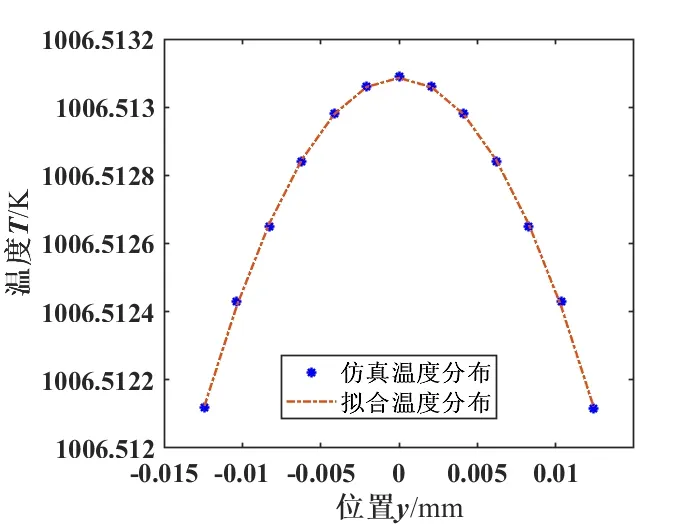
图6 金丝(Φ25 μm×2 mm)径向温度分布Fig.6 Radial temperature distribution of gold wire(Φ25 μm×2 mm)
若假设外界环境温度及键合丝两端的温度升高至353 K,即60℃时,仿真出来的最小直流熔断电流为1.306 A。升高至373 K,即100℃时,仿真值为1.276 A。可见最小直流熔断电流值随着外界环境温度的升高而降低。
2.2 最小直流熔断电流理论值与仿真值及实验值对比
2.2.1 金丝最小直流熔断电流对比分析
以下分析均采用外界环境温度为室温293 K,对流系数为50 W/(m2·K)。图7是利用公式(12)计算出的键合金丝的熔断电流的理论值与软件仿真出的熔断电流对比图。从图7中可以看到,金丝直径为20、30及38 μm,长度从0.5 mm到20 mm时,两者趋势符合较好,理论计算值略低于仿真值。图8为金丝最小直流熔断电流理论值、仿真值及实验值对比图。从图8中可以看出金丝直径在25 μm及50 μm处,软件仿真出的熔断电流值与Heraeu公司所给出的熔断电流实验值[15]符合很好。这两者的熔断电流值比理论计算出的熔断电流值都稍大一些,主要原因是理论分析时将轴向温度分布采用线性化处理所导致。图7和图8中的仿真值是理论计算值的1.15~1.27倍,并且该系数是随着键合丝直径的增大而增大。因此,用理论公式(12)计算出的熔断电流值乘以系数1.15~1.27可接近仿真值,也更接近实际的工况。
从图7、图8中可以看出,在其他参数不变的情况下,熔断电流随着金丝长度的增加而减小,随着直径的增大而增大。直径25 μm金丝在室温下理论计算的最小直流熔断电流随着对流系数的变化规律如图9所示,丝较短时对流系数影响不大,而在丝变长之后对流系数逐渐对熔断电流产生影响。同一长度时,对流系数越大熔断电流越大。
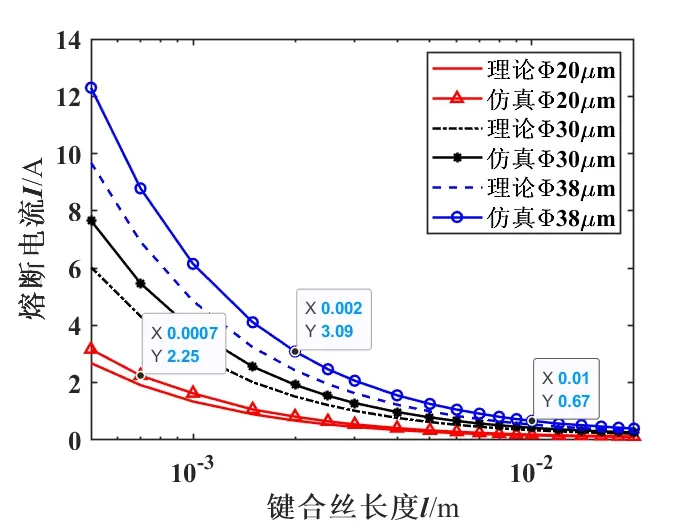
图7 金丝最小直流熔断电流理论值与仿真值对比Fig.7 Comparison of theoretical values and simulation values of the minimum DC fusing current of gold wires
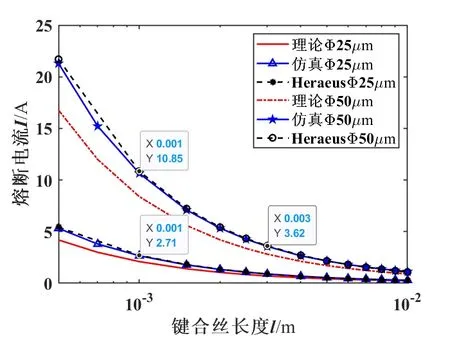
图8 金丝最小直流熔断电流理论值、仿真值及实验值对比Fig.8 Comparison of theoretical values, simulation values and experimental values of the minimum DC fusing current of gold wires
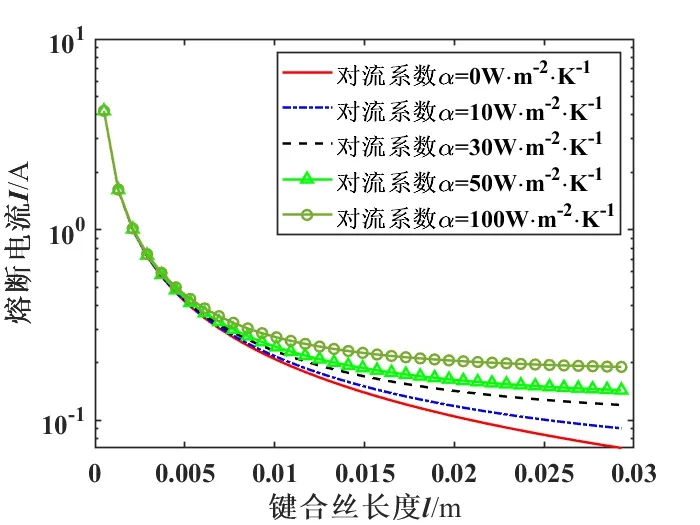
图9 金丝熔断电流随对流系数变化图Fig.9 Diagram of the minimum DC fusing current of gold wire for different convection coefficients
2.2.2 铜丝及银丝最小直流熔断电流对比分析
图10为利用公式(12)计算出的键合铜丝和键合银丝的熔断电流值与仿真值的对比图,图11为铜丝最小直流熔断电流理论值、仿真值及实验值对比图。
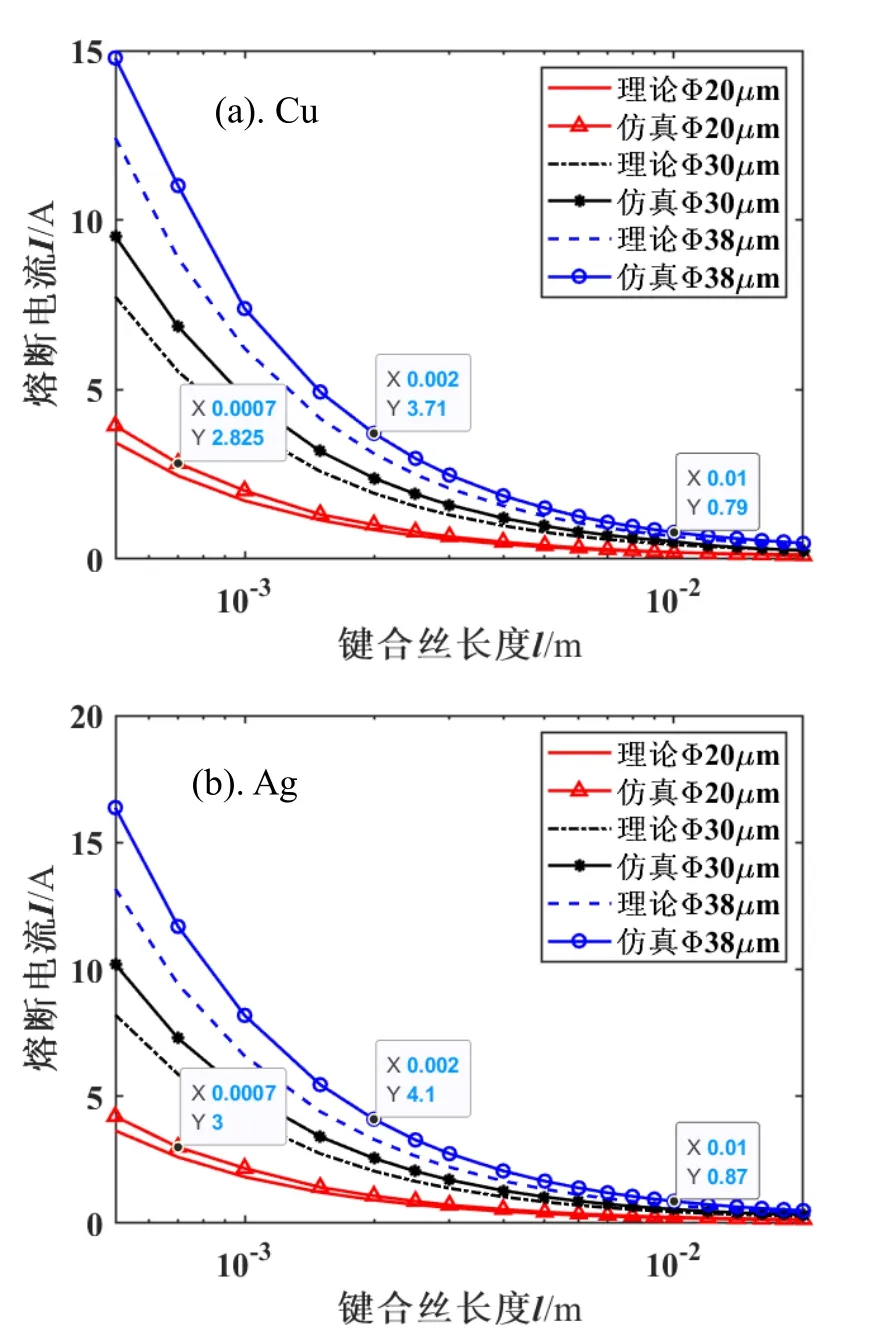
图10 铜丝和银丝最小直流熔断电流理论值与仿真值对比Fig.10 Comparison of theoretical values and simulation values of the minimum DC fusing current of copper (a) and silver wires (b)
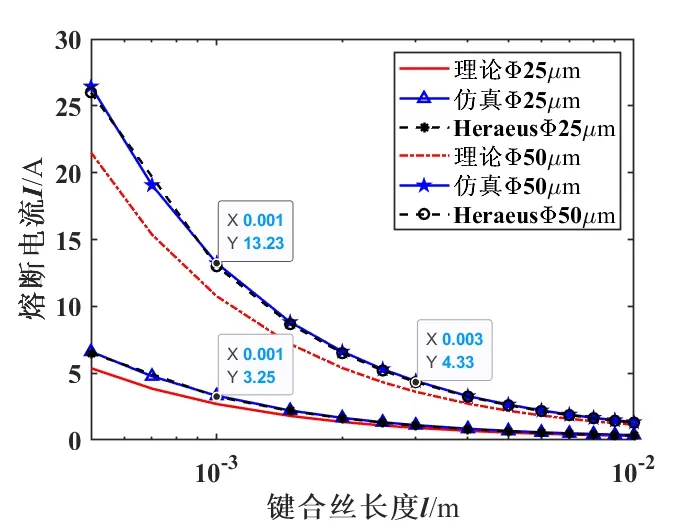
图11 铜丝最小直流熔断电流理论值、仿真值及实验值对比Fig.11 Comparison of theoretical values, simulation values and experimental values of the minimum DC fusing current of copper wires
从图10可以看到,铜丝或银丝直径为20、30、38 μm,长度从0.5 mm到20 mm时,两者趋势符合得也较好,理论计算值也略低于仿真值。从图11中可以看出直径25 μm铜丝在50 μm处,软件仿真熔断电流值与Heraeu公司[15]所给出的熔断电流实验值也符合得也很好。这两者的熔断电流值也比理论计算出的熔断电流值都稍大一些,原因与金丝情况相同。图10(a)和图11中铜丝熔断电流仿真值是理论计算值的1.03~1.24倍,图10(b)中银丝熔断电流仿真值是理论计算值的1.11~1.243倍。从图10、图11可以看出,当其他参数不变时,熔断电流值也随着长度的增加而减小,随着直径的增大而增大,该结果与键合金丝的结果一致。
2.2.3 三种键合丝的熔断特性对比分析
图12为三种金属键合丝在直径为25 μm时的最小直流熔断电流仿真值随长度变化对比图。显而易见,银的导电导热性最好,相同条件下,银的熔断电流最大,其次为铜,最后为金。
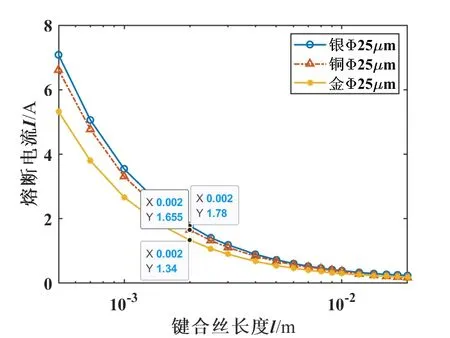
图12 金、银和铜三种键合丝最小直流熔断电流对比图Fig.12 Comparison of the minimum DC fusing current of gold, silver and copper bonding wires
3 结论
1) 当键合丝的材料特性参数、尺寸、环境温度及对流系数确定后,可利用公式(12)计算出键合丝在室温下的最小直流熔断电流值。在判断其为长丝或短丝后,可利用简易计算公式来计算熔断电流。
2) 仿真分析得出,键合丝中心温度最高,两端温度最低,并且沿轴向、径向的温度呈抛物线状分布。在对金、铜和银丝熔断电流分析后,发现仿真值与实验值符合得更好,而理论值相对较小的原因是分析时将沿轴向的温度分布线性化处理所导致。理论值乘以相应系数后可接近实验值。
3) 在其他参数均固定不变的情况下,键合丝熔断电流随着长度的增加而减小,随着直径的增大而增大。三种键合丝对比分析发现银的熔断电流最大,其次为铜和金。
