以结构化教学的视角关注课堂教学的一致性——以“整数乘分数”的教学为例

戴建杨

（义乌市实验小学教育集团 浙江金华 322000）

一、结构化教学、一致性的基本原理

教育家布鲁纳认为任何一门学科都有其基本结构，具体表现为各种定义、原理和法则，且随着学科基本知识和观念的不断扩大和加深而不断被提高和完善。数学的结构主要指向其学科内部知识各要素之间的逻辑关系，数学结构化就是将这些要素按学科逻辑体系进行连接、组合，以使各部分、不同要素之间的联系条理化、清晰化的过程。“一致性”指的是不同领域有不同要素的趋向相同，即指不同要素趋于相同的属性，“一致性”在英语中写为“alignment”，《韦伯斯特新世界字典》中将“align”定义为：形成一条直线；每个组成部分适当等同起来；达成统一，形成合作。因此，结构化教学与一致性原则，两者从本质上讲，都致力于将零碎的信息、松散的关系、点状化的联系，转化为紧密联结的结构化知识，形成一条前后贯穿的知识线。

二、课堂教学实践过程

本文以北师大版五年级下册第三单元第二课时探索分数乘法（二）为例，分析如何进行结构化教学。

（一）梳理乘法知识体系、聚焦乘法本质

追溯“乘法”，在北师大教材二年级上册第三单元第2 课时《儿童乐园》中，第一次接触乘法即整数乘法，将几个相同的数和可以写成乘法的形式，2×4 或4×2 表示4 个2 相加。那么这时，乘法意义就是求几个相同的整数和的运算。在第一学段中，无论是相同加数，还是相同加数的“个数”应该都是自然数。

在这一册的第七单元第7 课时《快乐的动物》中，学习了“倍的认识”，这几课的任务就是理解“倍”的意义，可以表示两个数量之间的数量关系（倍数关系），通过课堂中的圈一圈，理解把“标准”看成一份，比较的量有这样的几份，就是“标准”的几倍，这是解决求一个数的几倍的准备课，学会把“标准”看成一个整体，比较的量有几个这样的整体。

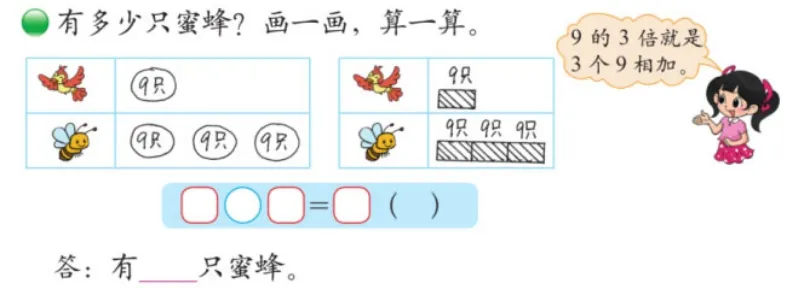
在这一单元的第8 课时《花园》中，学习了解决与“倍”有关的实际问题，通过画一画、算一算，理解求一个数的几倍，用乘法计算。此时的乘法意义又可以表示为求一个数的整数倍是多少。在第一学段中已经学习了乘法全部的意义，也就是求几个相同的整数和的运算或求一个数的整数倍。

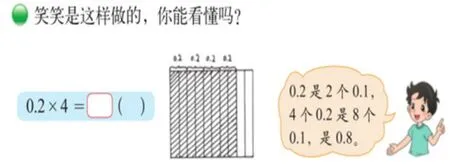
在第二学段中，继续学习乘法，在四年级下册第三单元第1 课时《买玩具》中，借助单价、数量、总价这三者之间的关系，通过借助面积模型，理解4×0.2 表示4 个0.2 相乘。

在这一单元第5 课时《蚕丝》中，1.2×1.25 表示1.2 的1.25 倍。此时乘法没有变，表示求几个相同的小数和的运算或求一个数的小数倍是多少，只不过在整数的基础上进行了数的扩充，从整数扩充到小数。

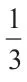
（二）联系旧知，寻求起点

【片段一】

淘气吃了6 块饼干，笑笑吃的是淘气的（ ），笑笑吃了多少块饼干？

师：抢答准备好了吗？

师：笑笑吃的是淘气的3 倍

生1：18 块

师：你是怎么想的？

生2：把淘气的饼干看成1 倍，笑笑有这样的3 倍，就是求6 的3 倍。6×3=18 块。

师：如果是2 倍呢？

生3：12 块，求6 的2 倍，用乘法计算。

师：如果是1.5 倍呢？

生4：就是求6 的1.5 倍，6×1.5=9 块。

师：为什么笑笑吃的饼干越来越少了呢？

生5：因为笑笑吃的饼干数量的倍数越来越少，所以吃的饼干越来越少。

师：这个倍数还可以少下去吗？

生齐：可以。

师：1 倍呢？

生齐：6 块。

企业标准化与质量管理体系通过PLM系统紧密结合到一起。企业质量管理体系确定各个过程的输入、输出、控制准则和所需资源、文件、记录，对于可由计算机完成的活动，将其嫁接到PLM系统，并将PLM各个模块的报表输出格式统一为质量管理体系要求的质量记录，形成一个在一定范围和层次上互相渗透的有机整体。

师：说说你是怎么想的？

……

布鲁纳认为，任何一门学科都有一个基本结构，它反映了事物之间的联系。“结构”是指学科的基本概念、基本原理以及它们之间的联系，是指知识的整体和事物的普遍联系。进一步地，懂得基本原理可以使学科更容易理解。从教学目标结构化的角度来看，一个数的整数倍，到一个数的小数倍，最后过渡到一个数的分数倍，其教学目标是一致的，就是求一个数的几倍（几分之几）是多少，这样乘法的教学就可以画上一个阶段性的句号。从乘法的原理上来看，这样的结构化教学，目的就是围绕乘法大概念展开教学，打通各个学段中整数乘法、小数乘法和分数乘法的意义，乘法意义就是求几个相同加数和的运算或者求一个数的几倍（几分之几）是多少。通过新旧知识进行恰当的类比，就能使整数乘分数这个知识点很好地融合到乘法知识结构当中，达到事半功倍的效果。

（三）点状联结，结构可视化

【片段二】

……

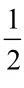
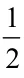
生3：我是这么想的，在五年级的时候，我们学过分率和倍数，分率和倍数都表示两个量之间的关系，只不过倍数是大于1 倍的，分率小于1 倍，我觉得方法是一样的。

生5：我不喜欢第一种方法，虽然也能得出用乘法计算，感觉这种方法太绕了。第三种画图的方法好像也太麻烦了！

师（小结）：求一个数的几分之几，其实就是求一个数的几倍，只是这里的倍数不到1 倍，我们习惯于说“几分之几”，而不是“几倍”，可见“几倍”和“几分之几”只是说法上的不同而已，本质上却是一样的。

……

美国教育学者奥苏贝尔认为，学生能否习得新知识，主要取决于他们认知结构中已有的有关观念，即通过新信息与学生认知结构中已有的有关观念的相互作用才得以发生的，这种相互作用的结果导致了新旧知识的意义的同化。因此，任何结构化的教学活动必须以已有的知识储备为基础，以现实情境为载体，在新旧知识通化中进行意义建构，使学生强化对数学本质理解、突出整体一致、形成数学体系的结构化。在这一教学活动中，笔者设计的情境中，无论从画图的方法，得到求一个数的几分之几用乘法计算，还是从标准量不变，比较的量从3 倍，到2 倍，到1.5 倍，逐渐过渡到笑笑吃的是淘气的，学生就能从一个数的几倍顺利类推一个数的几分之几。但更多的学生觉得求一个数的几分之几与求一个数的几倍方法是一样的。

结语

心理学家皮亚杰说过：“学生一旦形成某种结构，这种结构或者正在形成‘更强的’结构，或者由‘更强的结构’来给予建构。”因此，结构化教学可以使数学知识体系更加清晰，使教学过程前后联系更加紧密，促使学生将知识内化为认知，更有利于学生理解和掌握新的知识，使其学习更加高效。当然，实施结构化教学对教师也有较高要求：教师要重视对教学内容在大领域的视角下结构化分析，对教材重新研读、分析、解构，重组教材，加深对数学知识本质的理解，能建立数学知识间的结构与联系，由此建构出大领域学习主题统整下的脉络清晰、联系紧密的数学知识体系，进而引导学生体会不同数学知识之间的一致性和可迁移性。还要深入了解学生的基本学情，并具备较强的课堂调控和引导能力，帮助学生学会用领域的、联系的、发展的眼光看问题，能充分放手让学生经历知识的主动建构，让学习真发生。