绳牵引并联机构末端执行器运动轨迹精度评价方法
2023-01-21侯泽群李杨龙
李 航,彭 程,杨 芳,侯泽群,李杨龙
(河南科技大学 机电工程学院,河南 洛阳 471003)
0 引言
运动目标模拟装置能够实现特定目标的速度、轨迹等运动状态模拟,主要用于检验跟踪装备的跟踪性能,是装备从研制到应用过程中一种至关重要的测试设备。目前使用的运动目标模拟装置[1-2]结构形式多为串联结构,运动部件惯性较大、工作空间小,只能进行运动目标低速、简单轨迹的运动状态模拟,不能进行运动目标高运动状态(高速、急变速、急转弯)模拟,适用范围受到很大限制。
绳牵引并联机构是一种继承了刚性并联机构优点的新型并联机构,其使用质量轻的绳索代替传统的刚性支链。此类并联机构主要利用多根绳索来调控末端执行器位姿及运动轨迹,具有工作空间大、运动速度高、惯性小、结构简单等优点[3-5],在大型射电望远镜馈源支撑系统、飞行器风洞支撑系统、人体康复训练器、三维打印设备等方面得到应用[6-14]。
近年来,国内外学者在绳牵引并联机构末端执行器位姿测量方面进行了一些研究工作。文献[15]提出了一种结合绳索长度测量数据和角位移测量数据的数据融合方法,解决了通过测量绳索长度得到末端执行器位置精度不高的问题,获得了更为精确的末端执行器位姿。文献[16]开发了绳牵引并联机构视觉测量平台,编写了一种在线图像处理程序,对末端执行器的运动位置进行了实时跟踪,提取了末端执行器位姿数据。文献[17]提出了一套三维姿态伺服系统,可间接测量出末端执行器的运动姿态。文献[18]针对用于风洞试验的多自由度绳牵引并联机构,用双目视觉测量系统分别对3种典型运动轨迹下末端执行器动态位姿进行了测量。文献[19]提出了一种基于彩色编码的机器视觉位姿测量方法,实现了副油箱风洞模型的位姿动态测量。由于绳牵引并联机构还没有在运动目标模拟装置中应用,故极少见到与运动目标模拟相关的研究文献。
对于运动目标模拟装置,其末端执行器的运动轨迹精度直接影响了运动目标模拟的质量。本文针对用于高动态运动目标模拟的平面4绳牵引2自由度并联机构,基于末端执行器运动轨迹离散点测量数据,研究末端执行器运动轨迹精度评价方法,为提高末端执行器运动轨迹控制精度提供理论依据。
1 轨迹精度评价方法
针对运动目标模拟装置需要模拟的直线、抛物线和圆运动轨迹,研究基于最小二乘法的轨迹误差评价方法。
1.1 直线运动轨迹误差评价方法
基于最小二乘法[20]对直线运动轨迹误差进行评价,以最小二乘中线为直线运动轨迹的理想直线,与之平行的两条距离最近且包容实际轨迹线的平行线之间的距离为直线轨迹误差的最小二乘评价值。计算时以各测量轨迹坐标点偏差值的最小二乘法中线作为评价基线,求得评价基线两侧最远测量点至该基线的距离,即可求出末端执行器直线运动轨迹的误差最小二乘法评价值。
按照最小二乘法中线法评价直线轨迹误差,其误差值是唯一确定的,具体的步骤如下:
①求解出最小二乘法中线。设工作平面为XOY,平面内的直线方程可表示为:
y=kx+b,
(1)
其中:k、b分别为直线的斜率和在Y轴上的截距。
轨迹上各测量点为Pi(xi,yi),i=1,2,…,n,由最小二乘法原理,得到目标函数为:
(2)
然后,根据极值原理,要使式(2)的目标函数最小,即:
(3)
联合式(2)和式(3)可得矩阵方程:
(4)
由式(4)可得最小二乘法中线斜率k和截距b,所以,最小二乘法中线方程为:
(5)
②求各测量点Pi到最小二乘法中线的距离hi,如式(6)所示,然后分别找出两侧测量点至该中线距离的最大值hr-max和hl-max,进而求得末端执行器直线运动轨迹的误差值δl,
(6)
式(6)为点到直线的距离公式,本文不对其取绝对值,主要原因为:在该公式中当点位于直线的左侧时得到的hi为负值,点位于直线的右侧时得到的hi为正值,所有负值中的最小值即hl-max,所有正值中的最大值即hr-max,这样可以很方便地获得直线两侧最远点到直线的距离。
δl=hr-max+|hl-max|。
(7)
1.2 抛物线运动轨迹误差评价方法
基于最小二乘法对抛物线运动轨迹误差进行评价,首先使用最小二乘法拟合得到最小二乘法抛物线,然后计算出各实际测量点到最小二乘法抛物线的最小法向距离,得到外侧测量点到最小二乘法抛物线的最小法向距离中的最大值和内侧测量点的最小法向距离中的最小值,最后求出平面内抛物线运动轨迹的误差值。本文中定义最小法向距离为测量点与该点的抛物线法线与抛物线的最近交点的距离。轨迹误差评价流程如下:
①拟合出最小二乘抛物线。设平面内的抛物线方程为:
f(x,y)=Ax2+Bx+C-y。
(8)
抛物线运动轨迹上各测量点为Pi(xi,yi),i=1,2,…,n,根据最小二乘法原理得到目标函数为:
(9)
根据极值原理,要使式(9)的目标函数最小,有:
(10)
联合式(9)和式(10)可得矩阵方程为:
(11)
对式(11)进一步求解,可得最小二乘抛物线的A、B、C值,即可得最小二乘抛物线方程。
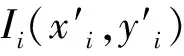
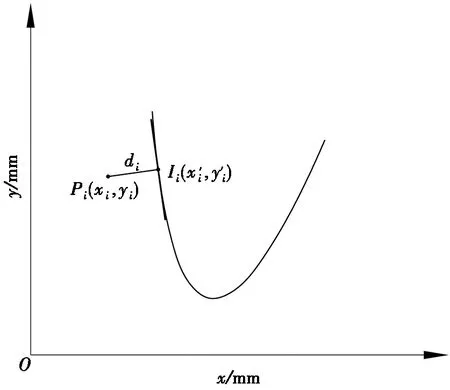
图1 轨迹测量点与最小二乘抛物线关系图
(12)
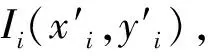
(13)
③判断各测量点在最小二乘抛物线的方位。根据抛物线的几何知识,通过计算测量点在最小二乘抛物线方程中值的大小,可以判断出各个测量点是位于抛物线的外侧还是内侧。将各测量点分别代入式(8),当f(x,y)>0时,表明测量点是位于最小二乘抛物线的外侧,此时di为正值;当f(x,y)<0时,表明测量点是位于最小二乘抛物线的内侧,此时di为负值。
④计算抛物线运动轨迹误差。将抛物线运动轨迹误差δp定义为外侧各测量点到最小二乘抛物线的最小法向距离中的最大值dmax与内侧各测量点的最小法向距离中的最小值dmin之间的差值,即:
δp=dmax-dmin。
(14)
1.3 圆运动轨迹误差评价方法
基于最小二乘法对圆运动轨迹误差进行评价,以最小二乘圆作为评价基准,求各测量点到最小二乘圆圆心距离的最大值和最小值,即可求出圆运动轨迹的误差值。如图2所示,坐标原点为O,设最小二乘圆的圆心为O′点,在坐标系Oxy中的坐标为(a,b),最小二乘圆的半径为R0。圆的轨迹方程可以表示为:
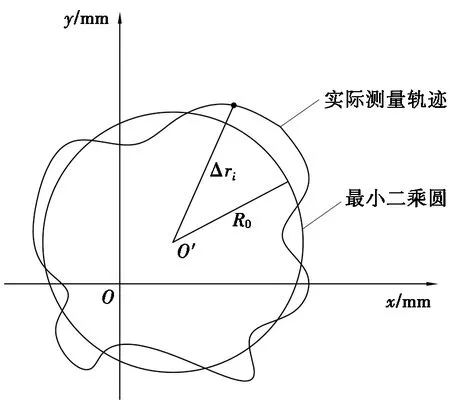
图2 最小二乘圆法
(15)
圆运动轨迹上各测量点为Pi(xi,yi),i=1,2,…,n,根据最小二乘原理得到目标函数为:
(16)
为了得到最小化问题的直接解,并且避免平方根,对式(16)进行改进,即:
(17)
进一步可化为:
(18)
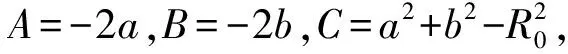
(19)
要使目标函数最小,即:
(20)
联立式(19)和式(20)可求得A、B、C,然后,根据式(21)可以求出最小二乘圆的圆心坐标和半径值,即:
(21)
定义各测量点到最小二乘圆圆心的距离Δri为:
(22)
圆运动轨迹误差δc为Δri中的最大值Δrmax和最小值Δrmin的差值,即:
δc=Δrmax-Δrmin。
(23)
2 试验及结果分析
2.1 末端执行器运动轨迹点测量方法
图3为绳牵引并联机构和末端执行器运动轨迹机器视觉测量系统。利用基于高速摄像机的视觉测量系统对末端执行器的运动图像进行采集和处理,获取末端执行器的运动轨迹离散点的二维坐标值。

图3 绳牵引并联机构和末端执行器运动轨迹测量系统
相关参数设置:运动图像分辨率为1 600 pixel×1 086 pixel,采集帧率为30帧/s,直线、抛物线、圆运动轨迹图像各采集3组。
2.2 运动轨迹测量数据分析和评价
末端执行器运动轨迹方程分别为:
直线运动轨迹方程:
y=x,x∈[-283,283]。
(24)
抛物线运动轨迹方程:
y=0.007 2x2-300,x∈[-283,283]。
(25)
圆运动轨迹方程:
x2+y2=4002,x∈[-400,400]。
(26)
对末端执行器运动轨迹离散点进行拟合,可得到末端执行器的实际运动轨迹,如图4、图5和图6所示。
利用第1节提出的末端执行器轨迹精度评价方法,分别对图4、图5和图6中测量轨迹所表示的数据计算其轨迹误差。表1、表2和表3分别展示了3种轨迹测量数据的相关计算结果。
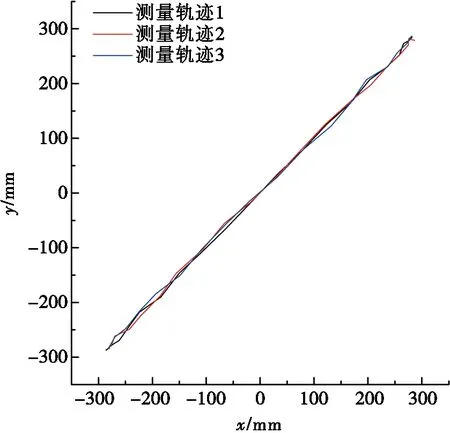
图4 直线运动测量轨迹
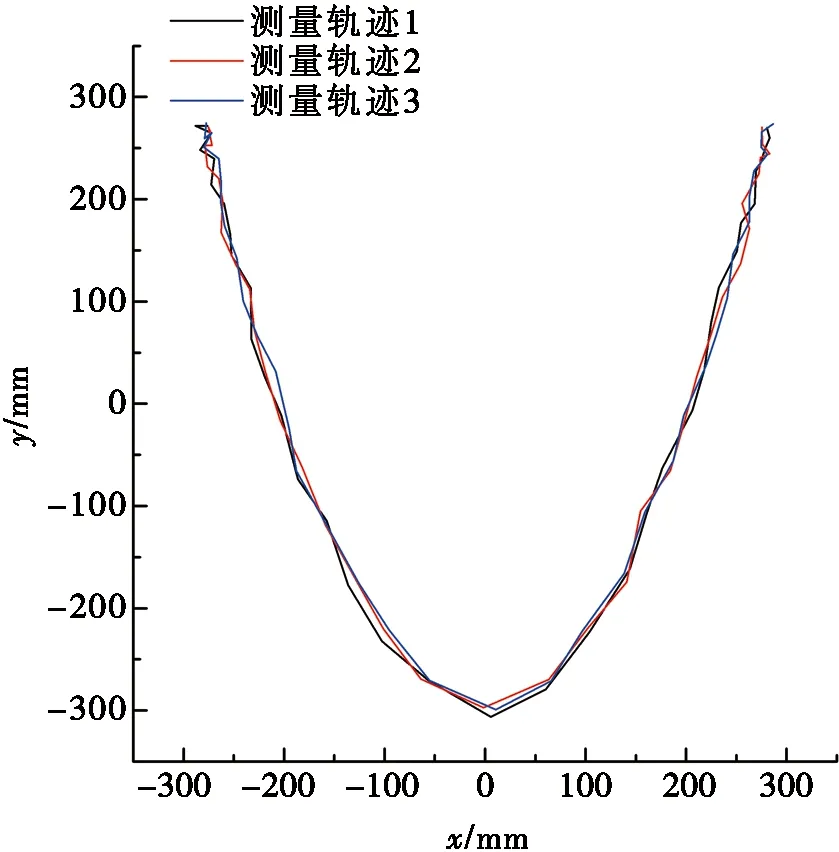
图5 抛物线运动测量轨迹
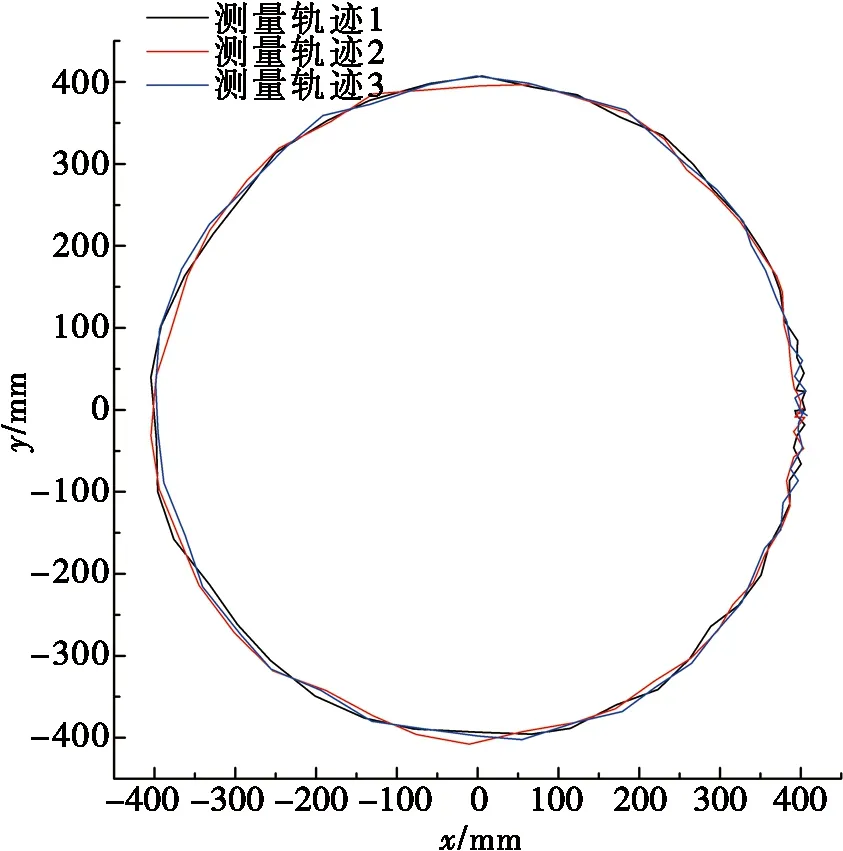
图6 圆运动测量轨迹
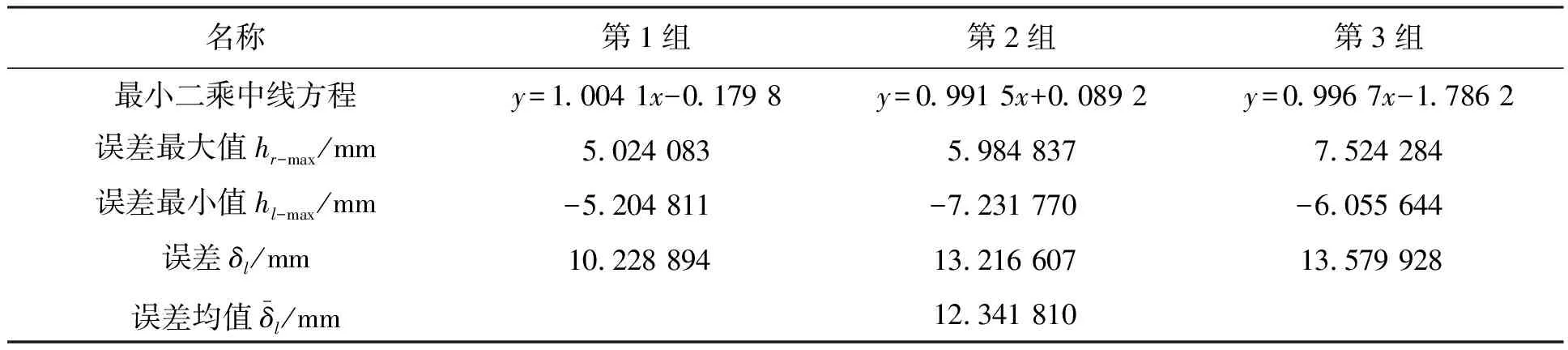
表1 直线运动轨迹误差计算结果

表2 抛物线运动轨迹误差计算结果
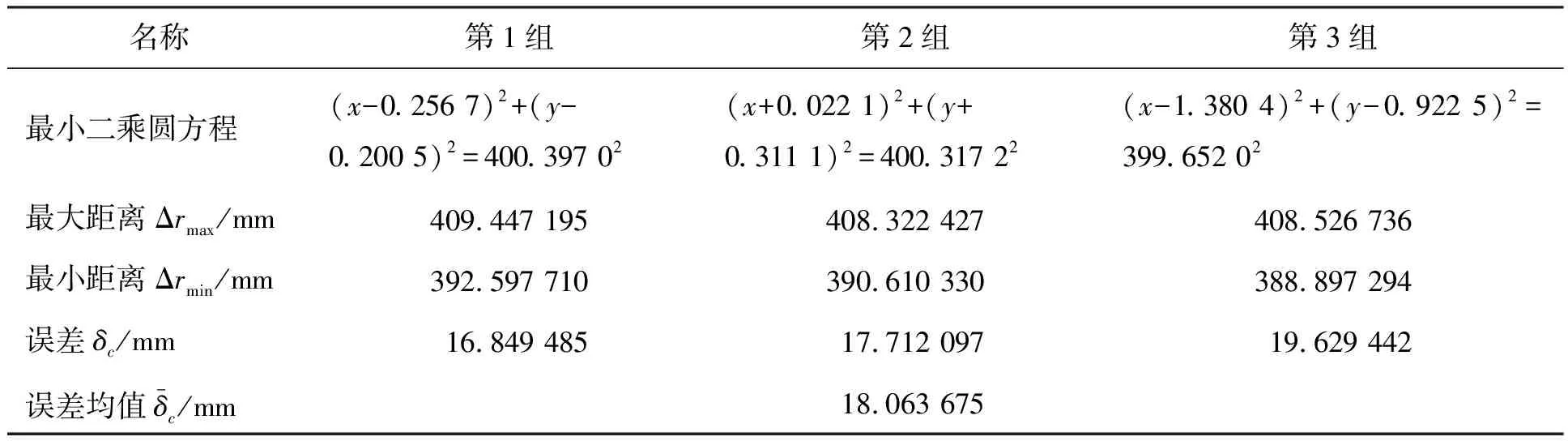
表3 圆运动轨迹误差计算结果
由表1~表3中的计算结果可知:直线、抛物线、圆3种运动轨迹的最大误差绝对数值分别为12.341 810 mm、16.428 087 mm、18.063 675 mm。为更好评判得到的误差能否满足装置的运行精度要求,在测量范围内对最大误差绝对数值进行进一步计算。
①直线运动轨迹误差:
(27)
其中:L为直线运动轨迹长度。
②抛物线运动轨迹误差:
(28)
其中:Lp为抛物线运动轨迹长度。
③圆运动轨迹误差:
(29)
其中:D为圆运动轨迹直径。
2.3 结果分析
由上述计算结果可以看出:分别对3种运动轨迹的测量数据进行计算,得到末端执行器直线运动轨迹误差为1.54%,抛物线运动轨迹误差为1.23%,圆运动轨迹误差为2.26%,圆运动轨迹误差大于直线运动轨迹误差,直线运动轨迹误差大于抛物线运动轨迹误差。
对轨迹误差产生的原因进行分析,主要原因有4个:
(Ⅰ)绳牵引并联机构试验样机的制造和安装误差。试验样机在研制时零部件的加工制造误差以及安装定位误差将直接影响到末端执行器的运动轨迹精度。
(Ⅱ)绳索弹性形变造成的误差。在末端执行器运动过程中,由于绳索受拉力会有弹性形变,导致绳索实际长度与理论计算长度之间存在偏差,从而使末端执行器实际运动位置与理论运动位置之间存在误差。
(Ⅲ)控制系统的控制误差。由于控制系统本身的制造误差再加上存在外界扰动使得期望输出量与实际输出量存在偏差,从而使运动轨迹产生了一定的误差。
(Ⅳ)测量系统的测量误差。由于测量系统中单目摄像机存在标定误差以及环境亮度等对测量系统的影响,导致测量值与真实值之间存在误差。
3 结束语
本文采用基于机器视觉的测量系统对绳牵引并联机构末端执行器直线、抛物线和圆运动轨迹进行了测量,基于最小二乘法对测量得到的运动轨迹离散点数据进行了计算,得到了3种运动轨迹的误差值,完成了末端执行器的轨迹精度评价,为提高末端执行器运动轨迹控制精度提供了理论依据。
