一种基于包含关系的Vague集新相似度量方法

冯卫兵，韩 玉

(西安科技大学 理学院，陕西 西安 710054)

0 引言

Vague集理论由Gau和Buehrer于1993年提出[1]，Vague集相似度量方法是其重点研究内容，用于判断两个集合之间的相似程度，进而判断大量数据间的关系。目前，学者大多从支持度和反对度出发[2-11]研究Vague集的相似性度量方法。

文献[5]通过对各元素取大取小来研究Vague集相似度量方法，文献[6]通过包含度理论来研究相似度量，但是这两种方法都只注重了数据之间的关系，没有考虑到未知度因素，导致丢失了很多有用信息。文献[7]对相似度量公式的每部分设置系数，文献[8]用函数来调节未知度系数，以此提高相似度量公式的度量能力，但是系数的合理选取还需进一步研究。

文献[9]从二次投票出发，考虑了二次投票中优势函数之差和两端点之间的距离因素，但是并没有考虑到二次投票后的未知度，造成一些数据无法有效区分。文献[10-11]同样从二次投票出发，分别对二次投票后的支持度和反对度进行取小，但该方法默认二次投票的结果就是最终的结果，不会再有三次投票，这说明其并没有考虑到二次投票后的未知度，即认为二次投票后不会存在弃权的结果。但事实上，二次投票后还是会存在三次投票的可能，所以导致某些度量结果与实际不符。目前为止，还是无法找到一个完美的Vague集相似度量方法，所以，继续寻找新的Vague集相似度量计算方法是十分有必要的。

本文从二次投票出发，同时考虑二次投票中支持度的包含关系、反对度的包含关系和未知度的包含关系，合理设置系数，提出了一种基于包含关系的Vague集新相似度量方法，并验证本文方法具有较强的区分能力。并将新方法应用于故障诊断等现实问题中，充分地说明了该方法的准确性与合理性。

1 Vague集基本概念

Vague值(集)的相关概念如下：

定义1[1]设有一论域X，X上的一个Vague集A是由一个真隶属函数tA(x)和一个假隶属函数fA(x)所确定的。tA(x)是从支持x的证据导出的x的隶属度下界，fA(x)则是从反对x的证据导出的x的非隶属度下界。πA(x)=1-tA(x)-fA(x)是Vague集A中元素x的未知程度。其中tA:X→[0,1]，fA:X→[0,1]，且对于∀x∈X满足tA(x)+fA(x)≤1。

定义2[1]若有x∈X，Vague集A在点x的Vague值为闭区间[tA(x),1-fA(x)]。当Vague集只有一个时，简写为x=[tx,1-fx]。

定义3[1]设A和B是论域X上的Vague集，∀x∈X，将A和B上的Vague值分别表示为A=[tA(x),1-fA(x)]和B=[tB(x),1-fB(x)]。则有：

A∩B=[tA(x)∧tB(x),1-(fA(x)∨fB(x))]；

A∪B=[tA(x)∨tB(x),1-(fA(x)∧fB(x))]，

其中：∨和∧分别是取大和取小运算。

2 一种新的基于包含关系的Vague集相似度量方法

2.1 一种新的Vague集相似度量方法

为了可以更准确地对Vague 值(集)之间的相似程度进行度量，本文展开了一系列讨论。

假设有一个Vague值x=[tx,1-fx]，那么可以将x用一个三元组(tx，fx，πx)进行表示，tx、fx、πx分别为一次投票中支持、反对和弃权部分的大小。考虑到在二次投票中，投票人会受一次投票结果的影响进行投票，所以最终可以将投票结果细化为(tx+πxtx,fx+πxfx,1-(tx+πxtx)-(fx+πxfx))，即表示二次投票中支持、反对和弃权的大小。

包含度理论[6]是描述相似度量的有效方法之一，但其通常会忽略未知度的影响。本文以二次投票为基础，借鉴包含度的理论，分别考虑了二次投票中支持度、反对度和未知度的包含关系，即对两轮投票后的支持、反对和弃权部分同时取小再求和，在此基础上提出了一种基于包含关系的Vague集新相似度量方法。

定义4 假设Vague集A上有Vague值x=[tx,1-fx]。tx是x的支持度，fx是x的反对度，πx=1-tx-fx是x的未知度，下面定义了新的二次投票中的支持度、反对度和未知度：

(Ⅰ)αx=tx+πxtx称为A中元素x的支持程度。

(Ⅱ)βx=fx+πxfx称为A中元素x的反对程度。

(Ⅲ)γx=1-(tx+πxtx)-(fx+πxfx)称为A中元素x的未知程度。

αx、βx和γx都可用投票模型来进行解释，如Vague值[0.2,0.5]表示在投票结果中，支持票占20%，反对票占50%，弃权票占30%。那么αx=0.2+0.3×0.2=0.26，可以解释为：第1次投票支持票为20%，受第1次投票结果影响，第2次投票可能还会有0.3×0.2=0.06的人支持。

同理，βx=0.5+0.3×0.5=0.65，可解释为：第1轮投票反对票为50%，受第1次投票结果影响，第2次投票可能还会有0.3×0.5=0.15的人反对。

同理，γx=1-0.26-0.65=0.09，可解释为：第1轮投票反对票为30%，受第1次投票结果影响，第2次投票可能还会有0.09的人弃权。

定义5 假设Vague集A上有两个Vague值x=[tx,1-fx],y=[ty,1-fy]。α、β、γ分别表示二次投票中的支持度、反对度和未知度。当tx≠0,fx≠0,ty≠0,fy≠0时，定义x和y的相似度MNEW1(x,y)为：

MNEW1(x,y)=λ1min(αx,αy)+λ2min(βx,βy)+λ3min(γx,γy)。

(1)

在该方法中，λ1、λ2定义为1或0。λ3定义为一个0～1的值，表示决策者在两轮投票后对信息识别的态度。λ3=1表示两轮投票后决策者的态度是完全支持。λ3=0表示两轮投票后决策者的态度是完全不支持。这里选取λ1=λ2=1，表示每轮投票总会有支持和反对的票，选取λ3=1/3表示在两轮投票后第3轮投票中弃权的概率是1/3。则确定系数后的相似度量公式如下：

MNEW1(x,y)=min(αx,αy)+min(βx,βy)+1/3min(γx,γy)。

(2)

当tx=0或fx=0或ty=0或fy=0时，式(2)不能很好地区分Vague集，定义x和y的相似度MNEW2(x,y)为：

(3)

最终得到x和y的相似度MNEW(x,y)：

(4)

式(4)为本文提出的一种基于包含关系的Vague集新相似度量方法。

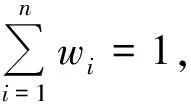
(5)

如果取wi=1/n，表明各元素的权重相同。

2.2 一种新的区分能力定义

已有的Vague集相似度区分能力通常通过分类数来定义。在已知相似度结果后，将数值相等的Vague集相似度量归为同一类，这样的类别越多，表明Vague集相似度量方法在该相似度量结果中区分能力越好。但是仅仅通过分类数这一个概念来度量Vague集相似度的区分能力显得太片面。因此，本文在此基础上，对小样本和大样本分别定义了新的区分能力公式。

定义7 设Vague集相似度为Mi(i=1,2,…,n)，对于小样本数据，定义新的相似度区分能力为：

(6)

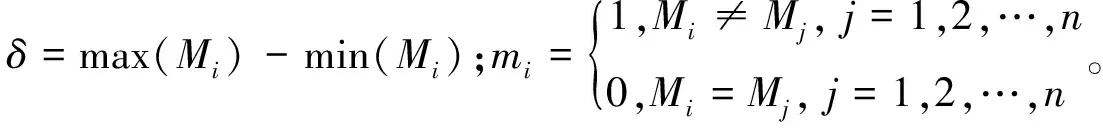
定义8 设有Vague集相似度Mi(i=1,2,…,n)，对于大样本数据，定义新的相似度区分值为：

D=f×(AVS-AVST)，

(7)

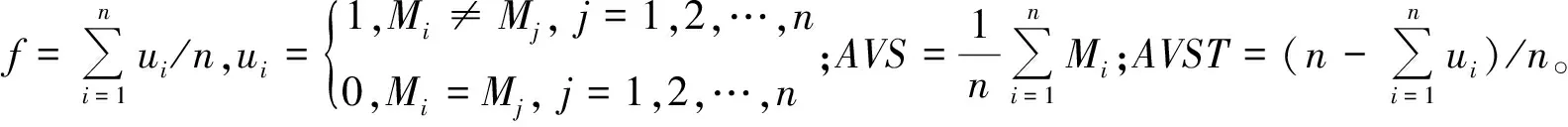
2.3 Vague相似度量性质

下面对部分相似度量性质进行证明。设有两个Vague值x=[tx,1-fx],y=[ty,1-fy]。MNEW(x,y)表示x与y之间的相似度。则MNEW(x,y)满足以下性质：

性质1 0≤MNEW(x,y)≤1。

证明当tx≠0,fx≠0,ty≠0,fy≠0时，

因为MNEW1(x,y)=min(αx,αy)+min(βx,βy)+1/3min(γx,γy)；

min(αx,αy)=min(tx+πxtx,ty+πyty)；

min(βx,βy)=min(fx+πxfx,fy+πyfy)；

min(γx,γy)=min(1-(tx+πxtx)-(fx+πxfx),1-(ty+πyty)-(fy+πyfy))，

则有

0≤tx+πxtx+fx+πxfx+1/3(1-(tx+πxtx)-(fx+πxfx))≤1；

0≤ty+πyty+fy+πyfy+1/3(1-(ty+πyty)-(fy+πyfy))≤1，

所以，0≤MNEW1(x,y)≤1。

当tx=0或fx=0或ty=0或fy=0时，

αx-βx=tx+πxtx-(fx+πxfx)=tx(1+πx)-fx(1+πx)=(tx-fx)(2-tx-fx)=

-tx2+2tx+fx2-2fx=(fx-1)2-(tx-1)2，

因为0≤tx≤1，0≤fx≤1，0≤tx+fx≤1，

所以-1≤αx-βx≤1。

同理-1≤αy-βy≤1。即有0≤|αx-βx-(αy-βy)|≤2。

αx=tx+πxtx=tx(1+πx)=tx(2-tx-fx)=-tx2+(2-fx)tx，

因为0≤tx≤1，0≤fx≤1，0≤tx+fx≤1，

所以0≤αx≤1。

同理0≤βx≤1，0≤αy≤1，0≤βy≤1，即有0≤|αx-αy|+|βx-βy|≤2。

则0≤3|αx-βx-(αy-βy)|+3|αx-αy|+|βx-βy|≤12。

所以0+|γx-γy|+γx+γy≤3|αx-βx-(αy-βy)|+3|αx-αy|+|βx-βy|+

|γx-γy|+γx+γy≤12+|γx-γy|+γx+γy，

证得0≤MNEW2≤1。

综上所述，0≤MNEW≤1。性质1证毕。

性质2 ∀x,y∈A，MNEW(x,y)=MNEW(y,x)。

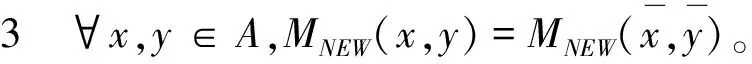
性质4 当x=y且γx=γy=0时，有MNEW(x,y)=1。

性质5 当x=[0,0],y=[1,1]或x=[1,1],y=[0,0]时，有MNEW(x,y)=0。

性质6 当x=[0,1]∈A且y=[1,1]∈A时，令MNEW(x,y)的值为区间[0,1]的任意值，记为∀[0,1]。

3 实例分析与对比

3.1 与现有Vague集相似度量方法的对比

本文选取代表性数据[5,9-10]对新方法MNEW与已有的方法进行比较，比较结果如表1所示。

表1中第9组Vague值[0,0]和[1,1]表示的是全部都反对与全部都支持的相似度为0；第10组Vague值[1,1]和[0.5,0.5]表示的是全部支持和一半支持一半反对的相似度为0.5；第11组Vague值[0,1]和[1,1]表示的是全部支持和全部弃权的相似度为[0,1]中的任何一个数。以这3组数据的相似度为前提构造了新的相似度量公式，并对其进行对比。

由表1可知：首先，MZX、MW和MG不满足上述前提条件；对于第1组和第8组数据，MZX和MJ无法区分；对于第12～14组数据，MG、MZ和MLY的相似度都为1，但这几组数据的Vague值是相等的，当未知度为0时(第12组)，未知度不产生任何影响，所有的度量结果都一样为1；但当未知度不为0时(第13～14组)，MZX、MJ、MW和MNEW可以体现出未知性。且以第13组与第14组为例，MZX的区分度为0.895-0.857=0.038，MJ的区分度为0.8-0.7=0.1，MW的区分度为0.790-0.740=0.050，MNEW的区分度为0.893-0.760=0.133，显然，MNEW的区分度大于MZX、MJ和MW的区分度。

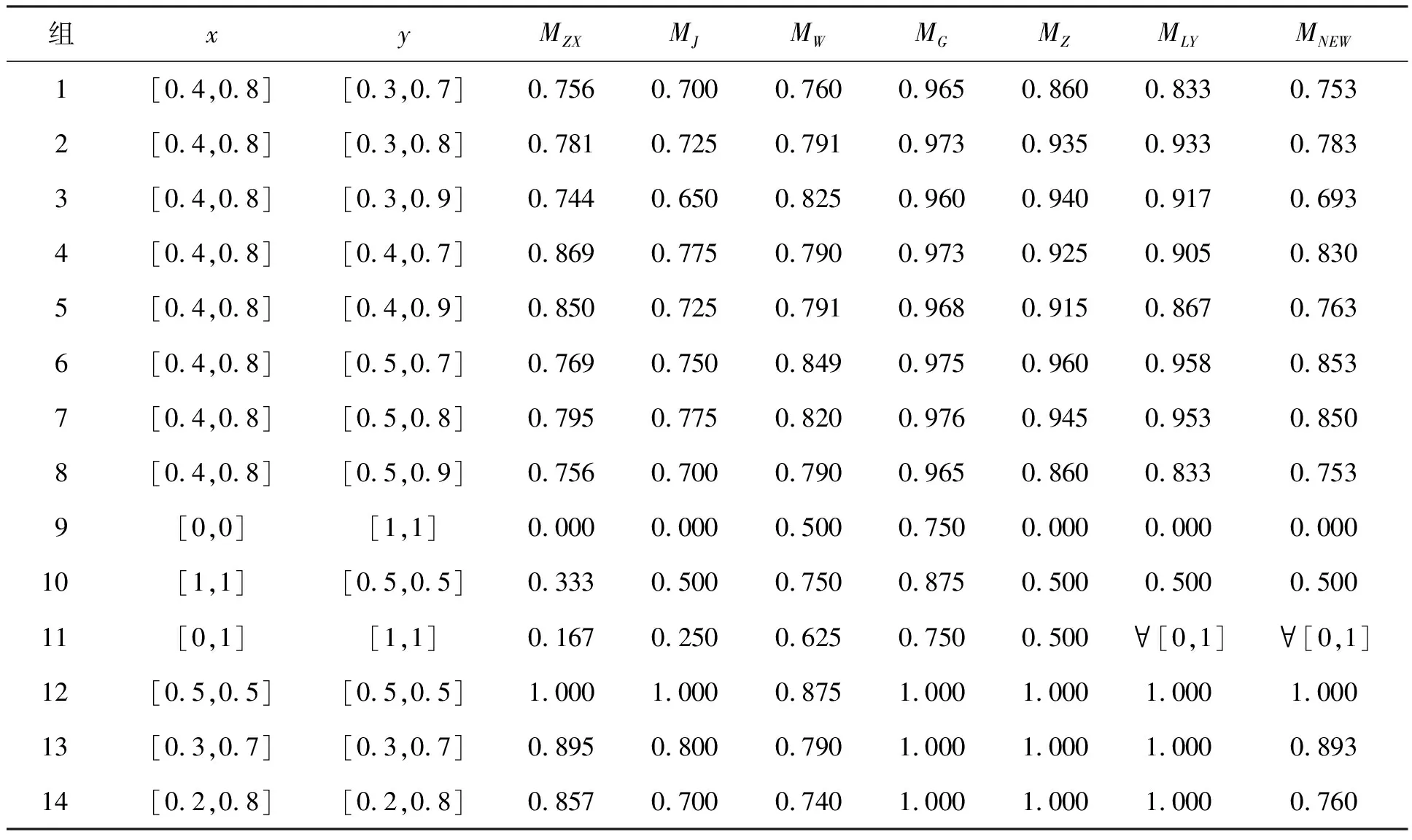
表1 各相似度量的比较

由于前8组数据是以Vague值[0.4,0.8]为中心，分别取与0.4相近的0.3，与0.7和0.8相近的0.7，0.9为新的tx和1-fx与其进行对比，所以前8组的相似度可以很好地代表各相似度的区分能力。下面结合定义7计算各Vague集相似度量方法的区分能力，计算结果如表2所示。

表2 各相似度量的区分能力

由表2可知：MZX、MLY和MNEW的区分度较高(都大于0.1)，但相比较而言0.140>0.110>0.109，即MNEW>MLY>MZX，所以MNEW的区分度较好一些。

3.2 增大数据容量后不同相似度量方法的对比

为了更好地说明新相似度量公式的合理性和有效性，本文扩大了数据范围，对上述几种Vague集相似性度量方法进一步进行研究。具体步骤[4]如下：

第1步：设有Vague值x=[tx,1-fx]，其中0≤tx+fx≤1，以0.1为步长找出[0,1]内符合要求的所有子区间，由此得到了60个Vague值。

第2步：将60个Vague值两两进行组合，得到3 600(60×60)组数据，去掉重复的组合(下三角矩阵中的组合)后，得到1 830组组合数据，将其称为数据集V。

第3步：结合文中给出的8种相似度量方法，对数据集中的数据进行相似度的计算。得到了1 830个计算结果，将其称为相似度集M。

第4步：结合定义8计算每种相似度量方法的区分值，为便于数据对比，将区分度的结果扩大一定倍数(此处不妨取1 000倍)，结果如表3所示。

表3 各相似度量的区分值

由表3可知：在同样的数据下，MZX、MW和MNEW的区分度较高(都大于60)。又因119.8>80.9>65.0,所以新提出的相似度量MNEW的区分能力更大一些。

4 数值模拟

4.1 模式识别

随着人工智能的发展，故障诊断等问题[12-15]的解决方法有很多，与Vague相似度量的结合使得故障诊断等问题被更有效地解决[16-20]。本文首先选取文献[16]中的模式识别案例进行讨论。

设有标准模式Ai(i=1,2,3)和待识别模式B：

A1=([0.8,0.9],[0.3,0.4],[0.6,0.8]);A2=([0.1,0.6],[0.7,0.8],[0.8,0.9]);

A3=([0.8,0.9],[0.3,0.4],[0.6,0.8]);B=([0.4,0.5],[0.6,0.7],[0.8,1.0])。

用本文中提到的Vague集相似度量公式进行计算，结果如表4所示。

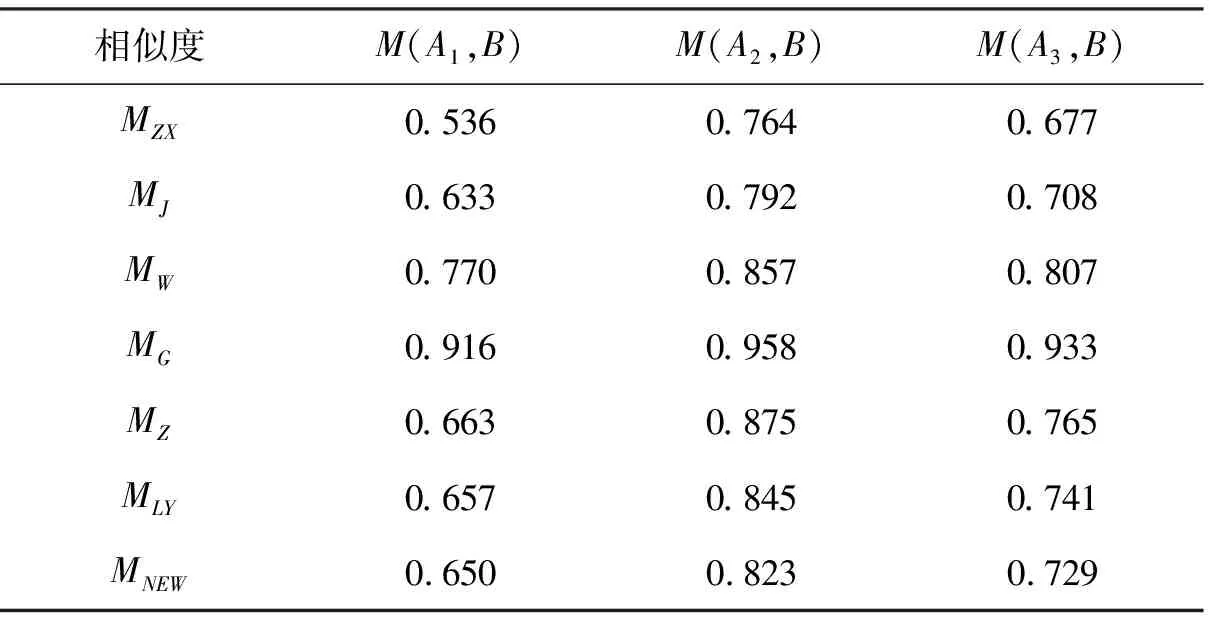
表4 模式识别结果比较

由表4可以看出：MZX、MJ、MW、MG、MZ、MLY和新的Vague集相似度量公式MNEW的模式识别结果是一致的，都为A2>A3>A1，且与文献[16]结果一致。因此，待识别模式B应该属于标准模式A2，表明MNEW的识别结果是合理的。

4.2 故障诊断

下面选取文献[13]中的水轮机故障诊断案例进行讨论。水轮机常见故障如表5[13]中第1列所示，水轮机不同频率如表5中第1行所示。现将表5中谱峰能量值作为Vague值展开计算。

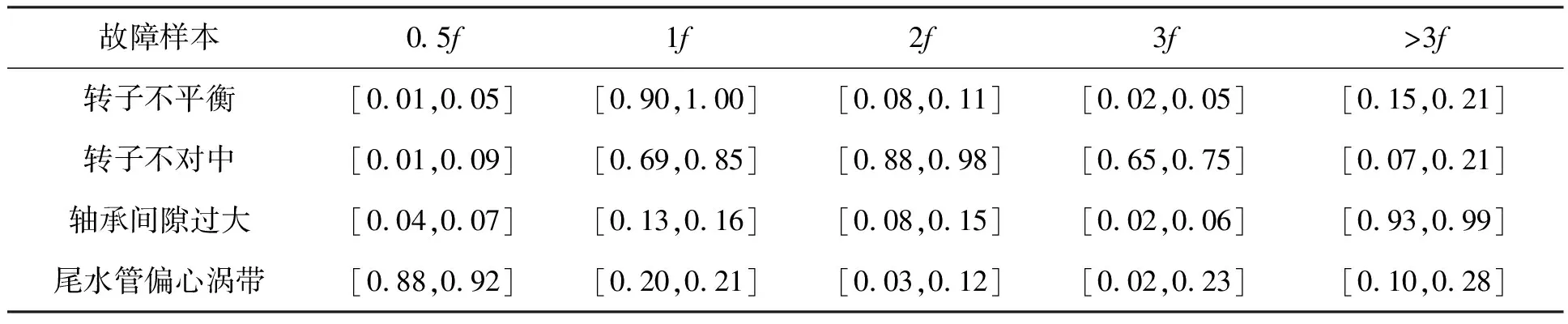
表5 系统故障知识

取第1次待诊断检测样本的Vague 集为：

D1=[0.04,0.04]/x1+[0.95,0.95]/x2+[0.10,0.10]/x3+[0.07,0.07]/x4+[0.04,0.04]/x5。

另一个检测样本得到的Vague集为：

D2=[0.90,0.90]/x1+[0.25,0.25]/x2+[0.12,0.12]/x3+[0.15,0.15]/x4+[0.25,0.25]/x5。

用本文中提到的Vague集相似度量公式进行计算，结果如表6所示。

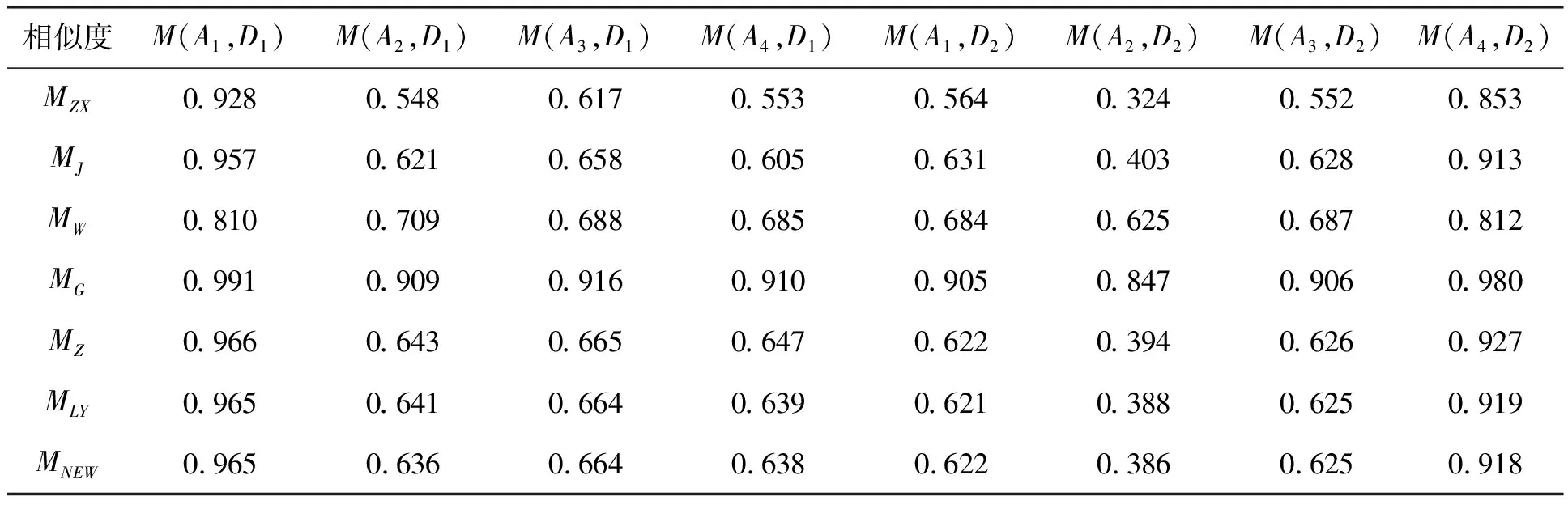
表6 故障诊断结果

由表6可以直观地看出：检测样本D1与A1的相似度最大(即属于故障转子不平衡)。检测样本D2与A4相似度最大(即属于故障尾水管偏心涡带)。该故障诊断结果与文献[13]诊断结果一致，说明MNEW的结果判断正确。

4.3 多准则决策

下面选取文献[9]中的空调系统选择问题进行讨论。已知有3种空调系统方案A1、A2和A3。3种准则C1、C2和C3，分别为经济、功能和有效性。决策者评价结果如表7[9]所示。

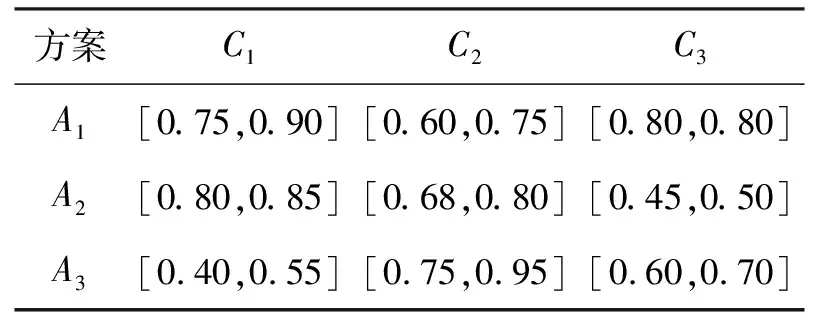
表7 决策矩阵

由表7可得理想方案为：

I={[0.80,0.90],[0.75,0.95],[0.80,0.80]}。

计算各备选方案与理想方案在相应准则下的相似度，如表8所示。

表8 多准则决策结果对比

由表8可知：在空调系统选择问题中，方案A1为最优方案，且所得结论与文献[9]一致，由此可见本文提出的相似度量方法MNEW是有效的。

5 结束语

随着Vague集理论研究的不断深入，寻找一个合理有效的相似度量方法也受到了人们重视。本文借助二次投票的含义，充分考虑了支持度、反对度和未知度3个方面的包含关系，给出Vague集相似度的一系列讨论。此外，通过数值算例和模式识别、故障诊断、多准则决策等应用说明了本文方法的有效性和可行性。所以认为本文提出的Vague集相似度量方法可以广泛应用于模式识别、近似推理和决策系统等研究领域。最后，由于Vague集存在不确定性，为此下一步工作将重点讨论未知度系数对相似度量影响的大小。