推进“理通练用”促成深度学习——新课标背景下教材“单元整理和复习”内容的教学实践与思考

蔡水华 丁群俐

（浙江省衢州市常山县育才小学）

《义务教育数学课程标准（2022年版）》（以下简称“新课标”）指出：“在教学中要重视对教学内容的整体分析，重视单元整体教学，帮助学生建立能体现数学学科本质、对未来学习有支撑意义的结构化的数学知识体系。”整理复习对学生知识技能的掌握、认识结构的建立和数学素养的提升有重要作用：对已学过的数学知识进行提炼升华，加深对知识的理解和联系；自主把零散的知识系统化，将趋于模糊的知识明晰化，提高数学知识和技能的实践应用能力。

“单元整理和复习”所要关注的既是数学知识体系上的一个面，也是知识结构中的一条线，面和线均由许多个点组接而成。因此，整理复习课的教学要综合考虑教学内容、学生实情、教师素养等多方面。我们有效组织实施“理通练用”四步教学模式，通过理、通、练、用的深入推进，来实现激活、疏通、感悟、提升。如图1 所示，为达成整理复习课中深度学习的“四步曲”。

图1

一、理——在梳理中盘活知识点

作为整理复习课，首要任务就是梳理知识，因为有效的知识点重现是必需的，但是如何有效激活盘存于学生大脑中的知识点呢？教师需要积极营造有利于学生回想的有效情境，促进整理复习活动走向深入。实践表明，在教学中需要教给学生一些梳理知识的方法，让学生在学习过程中主动去整理，从而盘活认知体系。在教学中，教师可引导学生利用整理复习单、思维导图、结构框架图、树形图等方法进行回顾整理，激发学生对所学知识的自主梳理和罗列盘活，提升学习能力。

例如，在学习了“分数和百分数”后，教师可让学生结合小数等相关知识进行自主整理，通过学生的合作交流、探讨汇报和补充完善。教师积极引导，学生个性呈现，共同梳理、提炼出框架图（如图2），这对于培养学生的兴趣以及结构化的建构都是大有裨益的。

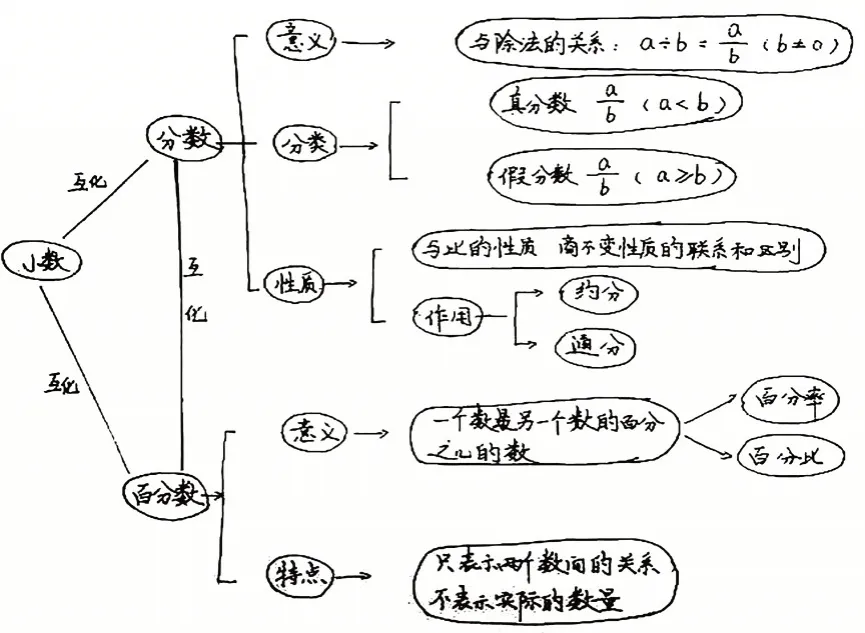
图2

同样，在五年级的“平面图形的面积”整理复习教学中，通过教师引导，学生逐步自主构架出各图形间的树状关系（如下页图3）。从结构清晰的图形树中可以直观地看出，各平面图形面积间的关键联结之处——一组底和高，可视作这棵图形树的根。在这样的过程中，学生自主地理出了知识体系的根脉，有利于学生对知识体系的深度把握和建构。

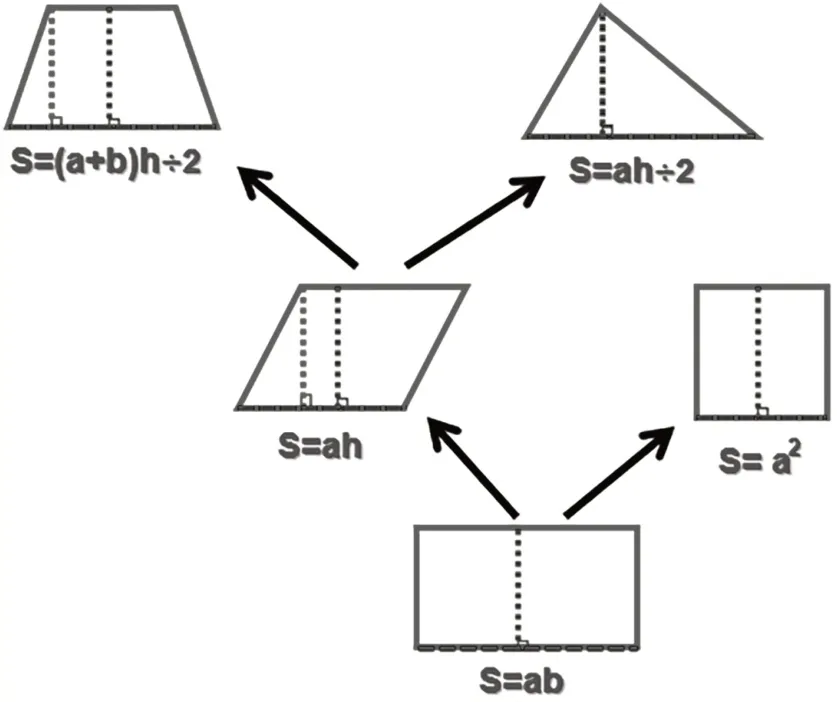
图3

二、通——在沟通中完善知识链

在整理复习课中，疏通也是关键一环，在学生进行有效梳理的基础上，教师要引导学生通过“辨一辨”“联一联”等过程自主创造知识链，开展自主合作、探索交流，促发思维碰撞，让学生站在更高起点、更深层次去系统、全局地理解和感悟知识，完善认知体系，形成自主建构的意识和能力。

以“四则运算”整理复习为例，教师可在学生自主梳理、交流互助的基础上，引导他们感悟知识之间的纵横联系和相互作用，逐步归纳整理，内化形成个性化的知识结构网（如图4）。

图4

在“平面图形的面积”整理复习课中，教师可让学生在边长为1 cm 的方格图中画出高为4 cm，面积为20 cm2的梯形。并在自主练习后进行反馈交流。学生会利用梯形面积公式倒推出梯形的上下底之和为10 cm 即可。随后，梯形上、下底的长度可以是整数，也可以是小数，从而得出可以有无数种方法（如图5）。然后，教师请学生仔细观察这些不同的梯形，说说发现的规律：从左往右看，梯形的上底变得越来越小，慢慢接近于“0”。当梯形上底为“0”时，就变成了三角形，它的面积也可以用梯形面积公式“（0+10）×4÷2”来计算……通过自主沟通，整体融合，学生惊奇地发现：这些平面图形的面积公式可相互融通变换（如图6），都可以用梯形的面积公式进行推导计算，它成了“通用公式”，数学就是这么奇妙。

图5

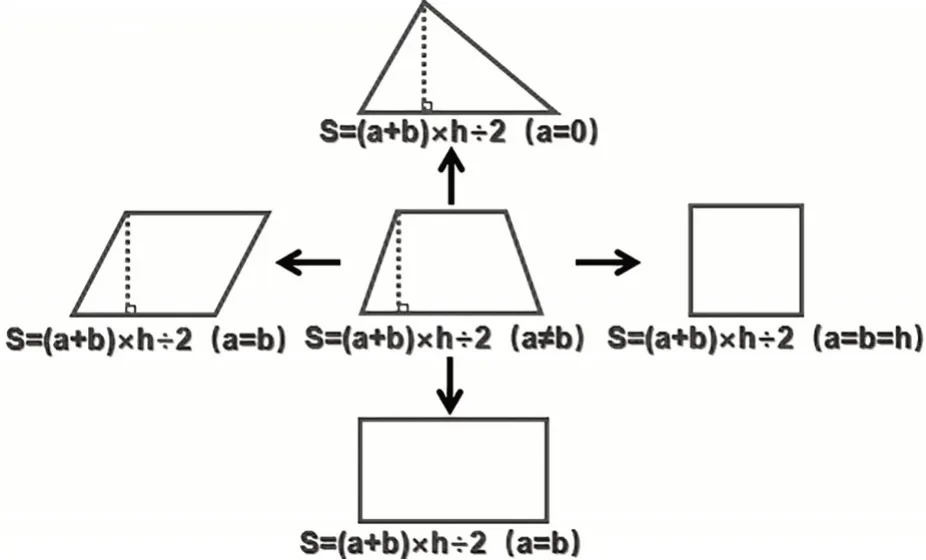
图6

这样，通过建立知识纵横结构网，让学生在自主合作的知识梳理过程中，找到各知识点之间沟通的纽带和桥梁，让无序、松散的知识变得更加有序、系统，理解和感悟也更加通畅、深刻，切实提升学生合作交流、自主建构的能力和意识，发展数学素养。

三、练——在练习中拓延知识量

整理复习教学的实效保障就是有效练习。学生通过梳理盘活、疏通整合、渐进构架等自主化学习过程，知识遗忘有了缓解，数学理解和知识构架得到了有效强化。此时，必要的课堂练习应及时呈现。同时，练习的内容要关注性质、规律、算理或知识、技能间的纵横联系，突出典型性、实践性、普遍性、层次性、综合性和开放性。

例如，在“百分数”整理复习教学中，为增强学生对数量关系的理解感悟，使其深度把握关系式中相应量之间的联系，教师可利用“一题多变”题组练习来实现“练中求知，串知成链，深度练习，有机建构”的目的，切实提升练习实效，拓宽并延伸学生的知识储备量（如下页表1）。

表1 “百分数”整理复习教学“一题多变”题组练习

又如，在学习了“圆的认识”后遇到解决圆环面积的相关问题时，通过计算分析，再和梯形面积公式进行沟通联系，结合变形转化和直观演示，学生会惊奇地发现：可以把圆环转化成相应的梯形（如图7），再用梯形面积公式来求圆环的面积，梯形的上底为小圆的周长，下底为大圆的周长，高就是大、小圆的半径差。

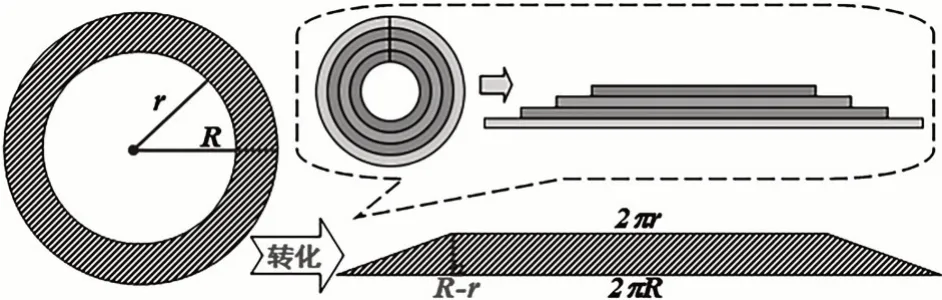
图7

四、用——在应用中提升知识观

理、通和练三个环节是学生掌握知识、形成技能、提升水平的重要途径，而用的环节更关注思维和意识的进阶，注重的是通过生活化的情境，唤醒学生已有知识技能和活动经验，激发学生的求知欲望和深度思考，让学生在解决问题的过程中内化提升。学生促进思和悟的提升，可逐步升华认知结构。

例如，在“百分数”的整理复习教学中，教师可引领学生回顾整个复习过程（如图8）。在知识的实践应用过程中，教师引导学生利用迁移、推理和对比，关注学生高阶思维的激发，进一步强化数量关系的分析与理解，将相对独立、散状的知识“点”“块”内化融合，促进知识体系的自然联接和有机延伸，形成知识体系的“线”“面”“体”，促进结构化、系统化，提升知识的综合运用能力和水平。

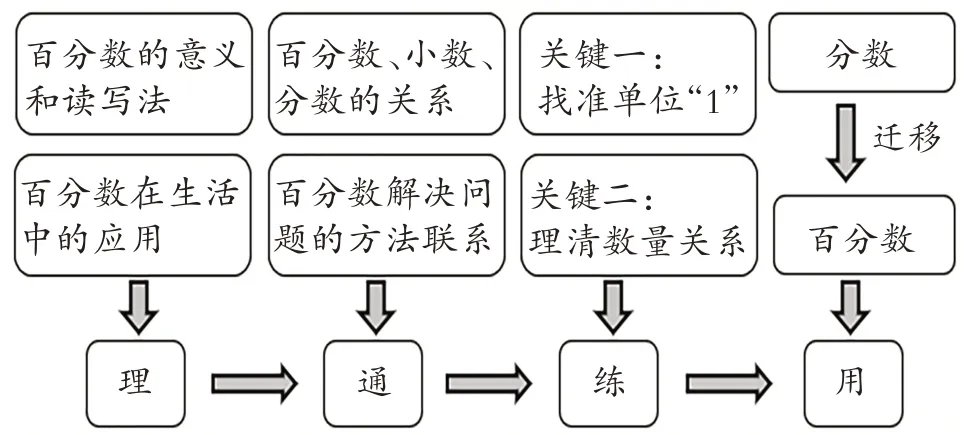
图8

新课标指出，数学教育应从学生的生活经验和已有的知识背景出发，向其提供充分的从事数学活动和交流探索的机会，通过活动使学生在学习过程中获得积极的情感体验。因此，在“单元整理和复习”教学中，教师要针对知识的重难点、学习的薄弱点、学生的盲障点，坚持相信学生，学会放手；给予空间，学会等待；开放协作，深度学习的原则，给学生创造空间，弥补缺漏，消除疑惑，让学生学会思考、学会自主、学会解决问题，促成对经验的自主感悟，达成体验成功，深度学习，发展能力，增强素质的目的。