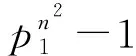剩余类环上全矩阵环的拟零因子图性质

赵寿祥，唐高华，南基洙

(1.大连理工大学 数学科学学院，辽宁 大连 116024；2. 桂林师范高等专科学校 数学与计算机技术系，广西 桂林 541199；3. 北部湾大学 理学院，广西 钦州 535011)

令R是一个环。为研究环性质与图性质之间的关系，人们在环上按照一定关系定义了多种图(无向图和有向图)。如，1988年，Beck[1]将环的所有零因子作为图的顶点，引入交换环上零因子图的概念，进而研究环的着色问题。1999年，Anderson等[2]改进了交换环上零因子图的概念，把环的所有非零零因子作为图的顶点，并规定2个顶点相连当且仅当这2个顶点的乘积等于零，他们还研究了环性质与图性质之间的一些关系。2002年，Redmon[3]将环的零因子图概念推广到非交换环，即将环的所有非零零因子作为图的顶点，并规定从顶点x到顶点y有一条边x→y相连当且仅当xy=0。2008年，Behbood等[4]引入环的强零因子图概念。2015年，Alibemani等[5]引入环的零因子理想图概念。文献[6-8]研究了矩阵环和群环上的零因子图和中心图的性质。文献[9-13]分别研究了高斯整数环、群环、矩阵环的性质与图的性质之间的联系。文献[14]引入环的拟零因子图概念。文中图论和代数相关知识可参看文献[15-16]。

对于环R中元素a，如果存在环R中一个非零元素b，使得aRb=0或者bRa=0成立，则称元素a为环R的一个拟零因子。如果把环R中所有非零拟零因子组成的集合作为图的顶点集合，并规定从顶点x到另一个顶点y有一条边x→y相连当且仅当xRy=0，称这样得到的图为环R上的拟零因子图，记为Γ*(R)。

下面介绍一些本文要用到的概念。有向图G是指一个有序三元组(V(G),A(G),ψG)，其中V(G)是非空的顶点集合，A(G)是与V(G)不交的边集合，ψG是关联函数，它使G的每条边对应G的一个有序顶点对。有向图G的有向路径是一个有向的点边交错序列W=v0e1v1…vk-1ekvk，其中，vi∈V(G)，ej∈A(G)，边ej是从顶点vj-1到vj的边，0≤i≤k，1≤j≤k。对有向图G中的任意2个顶点x和y，如果都存在一条从x到y的有向路径，那么就称有向图G是连通的，否则称有向图G是不连通的。对于有向图G中的顶点x，所有形如x→y这样的边的数量总和称为顶点x的出度；所有形如y→x这样的边的数量总和称为顶点x的入度；顶点x的出度和入度的和称为顶点x的度。从顶点x到顶点y的所有有向路径中包含边数最少的路径称为从顶点x到顶点y的最短路径。对于有向图G中的2个不同顶点x和y，从顶点x到顶点y的最短路径中的所有边数的总和称为从顶点x到顶点y的距离，记为d(x,y)。

在文献[14]基础上，本文研究剩余类环Zm上全矩阵环Mn(Zm)的拟零因子图Γ*(Mn(Zm))的一些性质，分别给出矩阵A是图Γ*(Mn(Zm))中的顶点的充分必要条件，以及图Γ*(Mn(Zm))中任意2个顶点的距离等于1、2、3的充分必要条件。最后证明2个剩余类环上全矩阵环的拟零因子图是同构的当且仅当全矩阵环所在的剩余类环同构，且全矩阵环的阶数相同。

1 预备引理

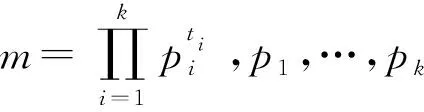
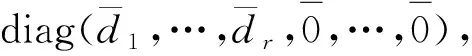
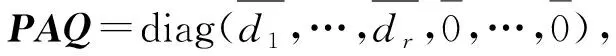
2 主要结果及证明

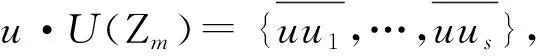
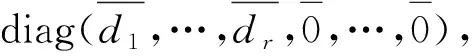
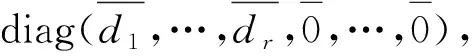
故A·Mn(Zm)·B≠0，即在拟零因子图Γ*(Mn(Zm))中从A到B之间不存在边相连，这与A→B矛盾。因此，假设不成立，即命题成立。证毕。

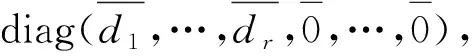
推论1拟零因子图Γ*(Mn(Zm))是一个空图当且仅当剩余类环Zm是一个域。

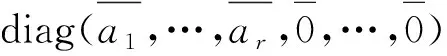
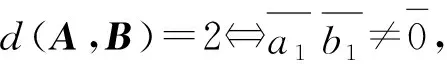
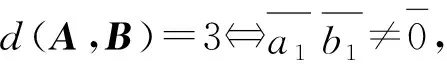
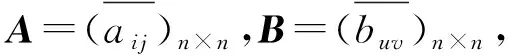
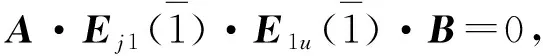
其次证明 ②。

进而d(A,B)=2。

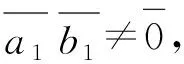
A·Mn(Zm)·C=C·Mn(Zm)·B=0

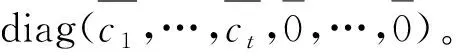
最后，由Γ*(Mn(Zm))的直径小于等于3和结论 ①、②就能得到 ③。证毕。

推论2在图Γ*(Mn(Zm))中任取2个顶点A=(aij)和B=(buv)，以下结论成立：

①d(A,B)=1⟺d(B,A)=1；

②d(A,B)=2⟺d(B,A)=2；

③d(A,B)=3⟺d(B,A)=3;

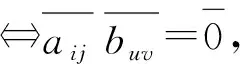
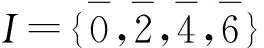
从例1可知剩余类环上全矩阵环的拟零因子图和剩余类环的子系统上拟零因子图之间并没有相互包含关系。

定理3设Zm1和Zm2为2个剩余类环,则拟零因子图Γ*(Mn1(Zm1))和Γ*(Mn2(Zm2))同构当且仅当等式n1=n2和m1=m2同时成立。

证明充分性显然成立。下证必要性。

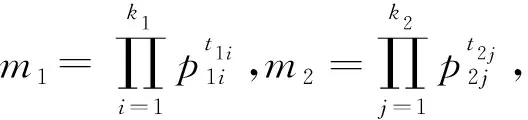
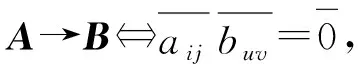
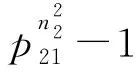
由定理3的证明过程可得以下推论3。