环Fq2+vFq2上的斜常循环码

王艳萍

自1994年，HAMMONS等研究二元线性码［1］以来，许多编码学者研究有限环.文献［2-4］研究不同环上的斜常循环码，讨论对应环上相关性质和结论.文献［5-7］构造自同构，讨论环上斜循环码的性质.文献［8］中研究环的MDS常循环码.本文研究上的Gray映射、斜常循环码及环上码的性质；在特定条件下，研究环上对偶码的性质.

1 准备知识

∀X=(x1,x2,…,xn)，Y=(y1,y2,…,yn)∈ℜn，定义=x1y1+x2y2+…+xnyn为X，Y的内积.

C是ℜ上长为n的码，它的对偶码：.

引理1［8］若C是ℜ上长度为n的线性码，令：

Cv=,vx+(1-v)y∈C}，C1-v=,vx+(1-v)y∈C}，则（1）Cv、C1-v是上的线性码，长为n；（2）C=，该表示唯一.

2 Gray映射

∀c∈C，c的Gray重量是WG(c)=WH(x,y)，且Φ是一保距双射.

定理1若C=是ℜn的线性码，则

∀x∈，有vx+(1-v)y=c′∈C⊥，对∀x′∈Cv，有vx′+(1-v)y′=c∈C，=vxx′=0⇒xx′=0，即.另 外，x∈，有c′=vx′+(1-v)y′∈C⊥，使 得=vxx′=0⇒xx′=0，.同 理可证，.

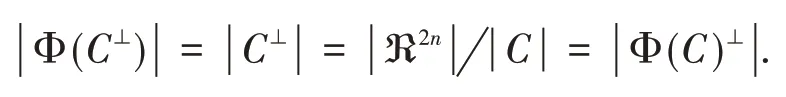
3 斜常循环码

定义1设λ是ℜ的单位，是ℜ上的自同构，为ℜn上的自同态，若 对∀c=(c0,c1,…,cn-1)∈C满足，称C为 斜 常 循环码（-λ-常循环码）.特别地，λ=-1，称C是斜负循环码；λ=1，称C是斜循环码.

注1：1-2v是ℜ上的一个单位，且有(1-2v)v=-v,(1-2v)(1-v)=1-v.

（1）是的理想；

（3）xn-(1-2v)是ℜ[x;]的中心.

其中（2）⇒（3）对∀f(x)=a0+a1x+…+，有.

其中（3）⇒（1）由定义可证.

下述结论均在引理2中（1）成立的条件下进 行；并假设θ为上 的 自同构，是ℜ的

设a=(a0,a1,…,an-1)，b=(b0,b1,…,bn-1)，则a∈Cv，b∈C1-v；又，，θ(bn-2))，得，则.

证明（1）证C=.

设g(x)=vg1(x)+(1-v)g2(x)，显然，；又g(x)∈C，即证C=.

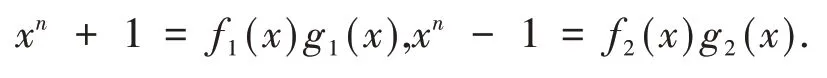
又(1-2v)v=-v,(1-2v)(1-v)=1-v，则

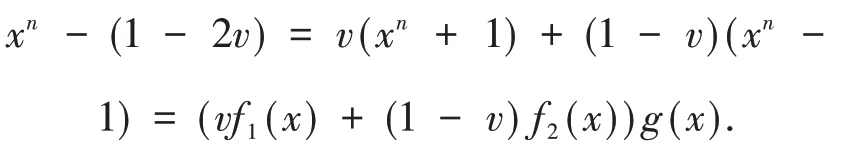
4 对偶码

（1）(a0,a1,…,an-1)和的系数向量正交；

（2）(a0,a1,…,an-1)与，…，及其-(1-2v)-常循环码移位正交；

定理4C是环ℜ上的线性码，则C为-(1-2v)-常循环码为-(1-2v)-1-常循环码.

证明“⇒”对∀u=(u0,u1,…,un-1)∈C，有.

则∀t=(t0,t1,…,tn-1)∈C⊥，有，t>，即

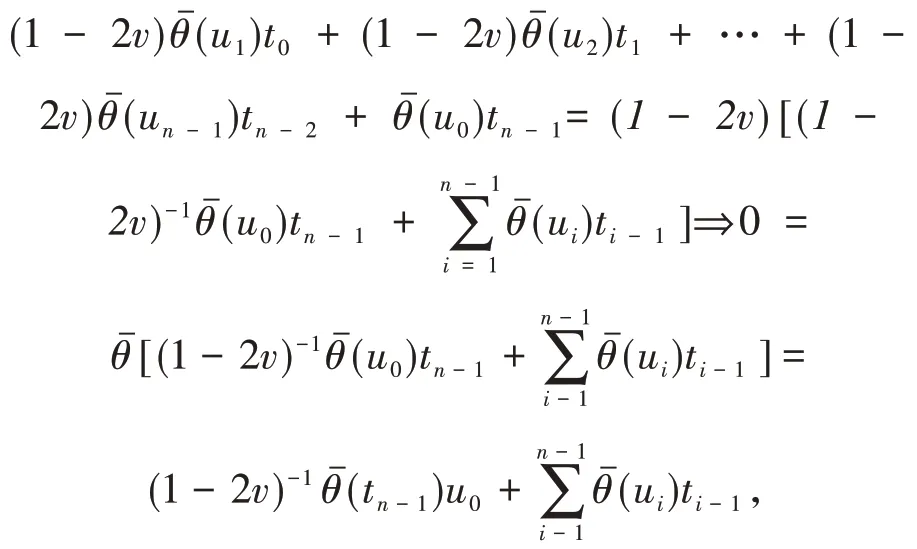
即

“⇐”同理可证.

定理5设C为ℜ的-(1-2v)-常 循环码，长度为n（偶数），C=，g(x)是首一的，h(x)=(xn-(1-2v))g(x)，则有

5 结语