指向深度学习的问题式教学设计研究*

王晶晶 占剑峰 何春玲通讯作者

（1.黄冈师范学院数学与统计学院 湖北黄冈 438000；2.黄冈师范学院生物与农业资源学院 湖北黄冈 438000）

引言

《普通高中数学课程标准（2017年版2020年修订）》中指出：提高从数学角度发现和提出问题的能力、分析和解决问题的能力，这使得“数学问题”在课程中处于更加核心的地位[1]。“问题式教学”是以“解决问题”为目标，以“提出问题”为引导，以“分析问题”为手段，帮助学生进行知识建构、问题解决的教学模式[2]。在教学过程中，教师应营造合适的问题情境，激发学生学习欲望的同时，引导他们进行自主思考和深入探究，从而达到分析问题、解决问题的目的[3]。

深度学习是指学习者以知识理解为基础，以问题解决为目标，批判性地学习新的知识和思想,将它们与原有的认知结构相结合，并将已有的知识迁移到新的认知情境中，进而达到对知识的深度理解和问题解决的学习[4][5]。深度学习要求学生能够从多个角度出发对知识进行全面的分析，强调创新能力和高阶思维的发展，学生在理解学习内容的基础上，带有批判性的眼光和质疑的思维面对新知识，将有助于加深对新知识的理解和掌握。

在当前的数学学习中浅层学习现象普遍存在，究其原因，主要是教学内容的碎片化导致学习的迁移度降低，不重视知识的形成过程以及忽视学生研究思路和研究方法经验的积累等方面。深度学习的前提是深度理解，而深度理解可以通过问题教学为手段。因此，教师在数学课堂中可以开展问题式教学，以“问题”为导向，创设一系列问题链推动课堂教学，引起学生深度思考，促进学生深度理解，从而实现深度学习。

一、教学内容分析

“诱导公式”是人教A版（2019）必修1第5章第3节的内容，本节课既是“任意角和弧度制”及“三角函数的概念”内容的延续，又是今后学习三角函数的图像与性质的基础，起到承前启后的重要作用。教材以“探究”和“思考”为核心，引导学生通过自主探究发现角的终边分别关于原点、坐标轴对称时，角也分别关于原点、坐标轴对称，进而得到点的坐标之间的关系，发现终边分别关于原点、坐标轴对称的角的三角函数值之间的关系.将诱导公式（数）与单位圆（形）紧密结合起来，形成利用单位圆的对称性研究三角函数性质的探究路径，进而发现和证明诱导公式，加深学生对三角函数的理解和掌握。

二、指向深度学习的问题式教学思路

对教材内容中的主要问题进行梳理后发现：要探究分别关于原点、坐标轴对称的角的三角函数值之间的关系，要经历四个研究过程：（1）建立角的终边之间的关系；（2）建立角之间的关系；（3）建立角的坐标之间的关系；（4）得到三角函数的关系。

依据上述研究过程，本节课以单位圆为载体，以问题式教学为主要教学模式，构建“圆的对称性→角的终边的关系→角的关系→坐标的关系→三角函数的关系”的研究路径。在问题情境环节提出诱导公式一的作用和反映圆的什么特性两个问题，引导学生深入体会圆的性质在推导诱导公式中的重要作用；在公式二的探究中，依据四个探究过程设置四个核心问题，继而将核心问题分解生成递进式问题链，引导学生逐步探究后得到诱导公式二；在公式三、公式四的探究中，引导学生类比公式二的探究思路，展开对公式三、公式四的探究，通过四个探究问题依次推导出公式三、公式四。

三、指向深度学习的问题式教学设计与实施

根据上述研究路径，将核心问题分解生成递进式问题链，引导学生进行知识建构，促进学生对所学知识的深度理解，进而实现深度学习。

1.创设情境，提出问题，引发学生思考

导入：“一切立体图形中最美的是球，一切平面图形中最美的是圆”，这是数学家毕达哥拉斯的一句名言.前面我们就利用单位圆得到了三角函数的定义，并且由定义推导出了诱导公式一，大家还记得吗？

问题1：诱导公式一有什么作用？

问题2：反映了圆的什么特性？

师：圆的性质还有对称性，对称性也是函数的重要性质.那我们可以借助单位圆的对称性来研究三角函数的对称性吗？

设计意图：三角函数的定义是学习诱导公式的基础，以诱导公式一反映的周期性出发，引出利用单位圆的对称性开展三角函数的研究，帮助学生规划研究方案，打开研究思路。

2.实践探索，分析问题，生成“问题链”

探究1：角α，π+α的三角函数值之间有什么关系？

（1）建立角α，β的终边之间的关系

问题1：在平面直角坐标系中，圆有哪些对称性？（关于原点、坐标轴对称等）

追问：当单位圆关于原点对称时，你能作出点p'，使其与点p关于原点对称吗？如图1所示：

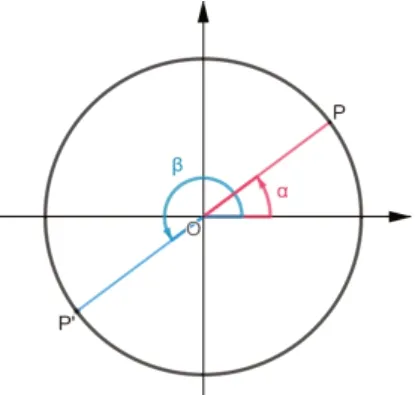
图1

（2）建立角α，β之间的关系

问题2：角β与角α有什么关系？它们的三角函数值分别有什么关系？

教师引导：要研究角的三角函数值的关系，要先研究角的关系。那么你能用α表示一个以op’为终边的角吗？

预设：π+α.

追问1：角β和角π+α有什么关系？

预设：以op为终边的角β都是与角π+α的终边相同的角，即β=2kπ+（π+α）（k∈Z）。

教师引导：根据公式一，终边相同的角的同一三角函数的值相等，因此可以先研究角π+α和角α的三角函数值之间关系。

（3）建立坐标之间的关系

问题3：设点p（x，y），根据点p’与点p关于原点对称，你能得到点p’的坐标吗？

追问：知道了点的坐标，应如何继续探究角的三角函数值的关系？

学生根据三角函数的定义，尝试写出角α与角π+α的三角函数式：

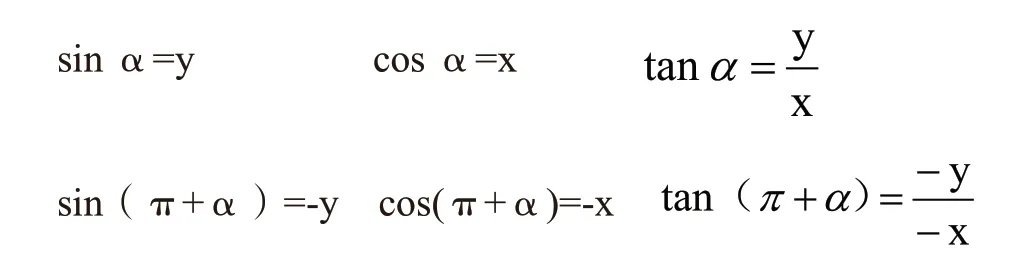
（4）三角函数值之间的关系

问题4：仔细观察角α与角π+α以及它们对应的三角函数值，你有什么特殊发现？

由此可得诱导公式二：

（5）梳理探究思路

问题5：回顾刚才的探究过程，你能说说我们是如何推导出诱导公式二的吗？

设计意图：探究过程以“问题”为主导，由浅入深，帮助学生在问题解决过程中感受逻辑思维和综合思维的发展。通过将核心问题分解成递进式问题链引导学生在实际的教学情境中全面、系统、深入地分析数学问题，为学生指明探索方向，促使学生对问题进行深度探索和剖析。在教学过程中注重诱导公式二的探究过程，引导学生建立起以单位圆为载体的诱导公式研究路径，为后续类比上述研究过程展开诱导公式三、公式四的研究做铺垫。

3.类比联想，深化问题，实现知识迁移

师：单位圆又关于坐标轴对称，根据公式二的探究思路，你能试着来研究一下三角函数关于坐标轴的对称性吗？

探究2：角α，-α的三角函数值之间有什么关系？

（1）建立角α，-α的终边之间的关系

问题1：应该如何作出点p关于x轴对称的点p'？

追问：角-α和角α的终边有什么关系？

（2）建立角α和角-α之间的关系

问题2：角α和角-α的三角函数值有什么关系？

教师引导：要想知道两个角的三角函数值的关系，要先知道角α和角-α的关系。

（3）建立坐标之间的关系

问题3：根据点p'是点p关x轴的对称轴，你能得到点p'的坐标吗？

追问：知道了坐标之间的关系，接下来该怎么做？

师生活动：教师引导学生利用三角函数的定义探究角α和角-α的三角函数之间的关系。

（4）三角函数值之间的关系

问题4：仔细观察角α与角-α以及它们对应的三角函数值，你有什么特殊发现？

由此推导出诱导公式三：

sin(-α)=-sinα，cos(-α)=cosα，tan(-α)=tanα

探究3：角π-α和角α的三角函数之间的关系。

师生活动：学生自主探究，并上台展示研究成果。

问题5：如何作出点关于轴对称的点p’？

问题6：角α和角π-α的三角函数值有什么关系？

问题7：根据点p’是关于轴的对称轴，能得到点p'的坐标吗？

问题8：仔细观察角与角π-α以及它们对应的三角函数值，你有什么特殊发现？

由此推导出诱导公式四：

sin（π-α)=sinα

cos（π-α）=-cosα

tan（π-α）=-tanα

设计意图：类比公式二的研究思路，引导学生自主开展公式三、四的探究，由教师引导变为学生自主探究，使学生进一步意识到数学的逻辑性和严谨性，深入体会研究思路和研究方法的一致性。

4.巩固应用，解决问题，促进思维发展

例1：将下列三角函数转化为锐角三角函数。

1问题1：你是怎么转化的？诱导公式起到了什么作用？

例2：利用公式求下列三角函数值。

问题2：解决这些问题时，你分别选择了哪个诱导公式？我们在解题时应该如何选择恰当的诱导公式呢？

设计意图：在例题教学中锻炼学生利用诱导公式进行求值、转化、化简的同时，引导学生体会解题的一般思路，明确利用诱导公式解决问题的思路和方法，促进学生对诱导公式及其作用进行深度理解，实现学生的深度学习。

四、指向深度学习的问题式教学设计反思

1.创设问题情境，激发学生探究欲望

一个好的问题情境能够引起学生深层次的思考和持续性的探究，并在学习过程中不断产生新的问题，引起深度思考和深度理解，从而实现深度学习。在实际教学中，教师应结合学习内容的本质，充分考虑学生原有认知水平和知识经验，创设恰当的情境，让学生在探究过程中带着问题思考。

2.设置核心问题，生成递进式问题链

核心问题是课堂教学活动的“主心骨”，也是传递数学知识、实现深度学习的重要途径，可以起到促进学生深入思考和探究的作用。教师在学生的最近发展区内，依据教学目标和重难点设计核心问题，再将核心问题分解生成递进式问题链，引导学生从小问题出发，逐个分析、逐个突破，一步步分析问题，直至解决问题。

3.构建研究路径，促进学生深度学习

问题式教学是以问题为核心，以问题解决为目标，引领学生感受知识的习得、建构的过程。在知识的建构过程中，通过问题式教学引导学生构建研究路径，然后根据研究路径和研究方法逐步展开探究，亲身经历知识的形成过程，从中感受问题解决的一般思路和方法，在满足学生探究欲望的同时，为他们开拓更广阔的深度思考空间，从而实现深度学习。