单裂隙隧洞类岩模型力学特性的数值模拟

杨治军, 刘泾堂, 胡金鑫, 邱成虎 洪 铭

(1. 甘肃省交通规划勘察设计院股份有限公司， 甘肃 兰州 730030；2. 长安大学 公路学院， 陕西 西安 710064)

自然界中岩体作为地层结构的主要组成部分，内部存在诸多形态的节理、裂隙，其分布的随机性与离散性决定了地下工程施工的复杂性。因此，为更好地研究地下岩体的力学特性，指导地下工程施工，诸多学者采用预制或切割加工技术制作含裂隙-孔洞模型，研究了预裂隙与孔洞周围的裂纹演化机理，并对多裂隙含孔岩石模型的破裂模式进行了一系列研究。其中，为了深入研究预裂隙空间分布形态与开孔类型对模型破裂模式的影响规律，部分学者采用控制因素法，通过改变预裂隙的数目[1～4]、间距[2]、倾角[3～6]、连通率[3,6]、粗糙度[7]等参数，得到各个条件下模型内部裂纹演化机理，进一步得出裂隙扩展存在开度阈值[8]。与此同时，部分学者通过控制岩体中的孔洞位置、数目、间距、大小、形状，进行模拟研究地下工程中岩体裂隙形态对孔洞围岩侧壁应力特征、裂隙扩展机理。其中，Cao等[9]采用单轴压缩试验和颗粒流程序相结合的方法，研究了开孔与节理的相互作用对开孔周围裂纹扩展行为的影响。Chen等[10]通过控制两条平行裂隙的间距与长度，研究了两种裂隙的扩展规律及相互影响。此外，裂隙倾角对开孔周围应力特征影响较大，Fan 等[11,12]通过预制含裂隙与圆孔组合的四类试件，分析了裂隙-圆孔组合试件的单向应力破坏特征及裂纹演化，进一步研究了裂纹倾角对圆孔周围主应力分布特征的影响。

近年来，随着科学技术的发展，研究手段逐渐多样化，使得研究复杂岩体力学问题得以实现。Wu[13]和刘享华[14]采用数字图像(Digital Image Correlation，DIC)技术进行非接触观测试件，研究了孔洞和裂缝质心之间不同水平距离对岩体力学性能的影响规律。陈伟[15]等人采用电镜扫描和XRD(X-ray Diffraction)衍射，得到了岩石在高湿环境水化作用前后的微细观结构变化和质量损失特征。武旭[16]等人采用声发射技术手段，研究了交叉裂隙对岩体力学、变形特征的影响，进一步得到裂纹扩展过程中能量演化机制。

实际隧道工程围岩均属于裂隙岩体，开挖后若不支护，极易出现变形、失稳等问题。目前，公路隧道暗洞一般采用复合式支护体系，由初期支护和二次衬砌组成。为此，部分学者以隧道支护体系为研究对象，探究支护结构对围岩力学性质的影响规律。其中，武东阳[17]进行了加锚类岩石的单轴压缩试验，得到锚杆对裂隙岩体的锚固效应及裂纹扩展约束作用。Fan[18]通过预制含衬砌的裂隙化隧洞模型，研究了衬砌结构对含裂隙类岩模型强度影响，进一步分析了不同裂隙组合类型下隧洞侧壁的主应力分布规律，得到衬砌结构受力薄弱点。由此可见，对于石膏类岩材料的力学特性研究较多[9～12]，且对裂隙尖端裂纹演化规律研究已较为成熟。但研究成果与实际岩体工程结合较少，工程实际意义不足。因此，本文基于现有研究成果，采用颗粒流模拟手段，通过控制单裂隙长度、角度及空间位置，对比分析各参数对隧道侧壁围岩受力特征的影响规律，进一步分析隧洞拱圈围岩加固原理，得出系统锚杆加固范围的理论公式，为隧道设计提供一定的理论依据。

1 数值模型方案及参数

隧道工程设计过程中，离不开对围岩物理、力学性质的前期勘察，但由于实际岩体力学性质的复杂性，使得工程施工具有较大的不可控风险。因此，可通过控制因素法，使得复杂的裂隙岩体力学、变形问题研究得以实现。近年来，诸多学者将石膏材料作为类岩材料进行了一系列研究[9～12]，其力学性质和破坏特征与泥岩、板岩极为接近。为此，本文在已有研究的基础上[18]，模型尺寸选取300 mm×300 mm(图1)。数值模拟采用单轴压缩试验，控制模型顶部与底部水平位移，两侧无约束。在数值模型中，隧道采用三心圆断面(图2)，并根据实际尺寸按1∶200比例缩小，即拱部半径R1由6 m等比例缩小为30 mm，其他参数类推。模型中隧道顶部范围布设单条裂隙，类型为张开型裂隙，宽度D=2 mm，模型其余参数见表1。其中，对于裂隙长度的研究(工况1)，控制裂隙角度α与裂隙位置H(H为裂隙与拱顶直线距离)，即α=0，H=30 mm，裂隙长度取L=10～50 mm；对于裂隙角度的研究(工况2)，控制裂隙位置H与裂隙长度L，即H=30 mm，L=20 mm，裂隙角度取α=0～90°；对于裂隙位置的研究(工况3)，控制裂隙角度α与裂隙长度L，即α=0°，L=20 mm，裂隙位置取H=10～60 mm(表2)。与此同时，隧洞拱顶至模型顶部布设测量点P1～P30(图1)，隧洞侧壁布设测量点，分别位于拱顶(T1)、右拱肩(T2)、右拱腰(T3)、右拱脚(T4)、拱底(T5)、左拱脚(T6)、左拱腰(T7)和左拱肩(T8)。此外，本文以石膏类岩材料标定的细观参数[18]为数值模拟依据，具体参数见表3。

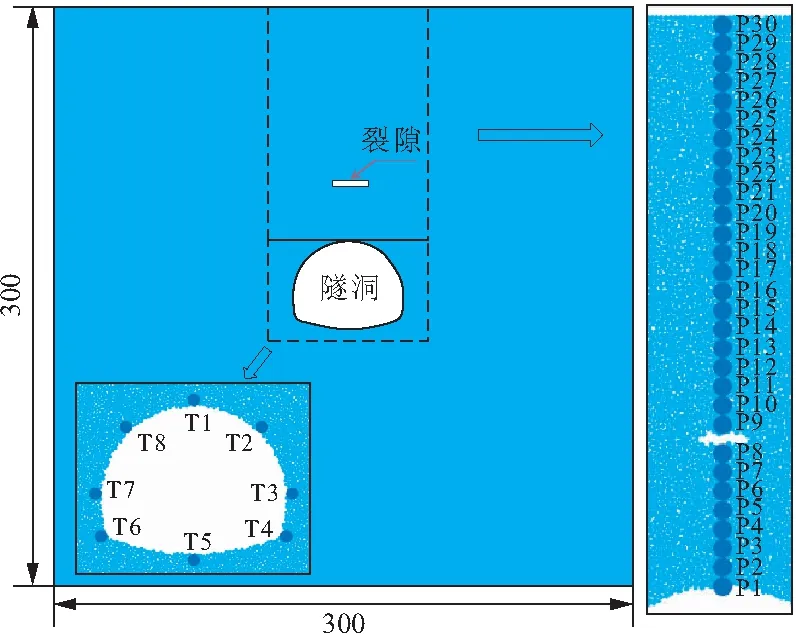
图1 数值模型宏观参数与监测点布设/mm

图2 隧洞与裂隙控制参数

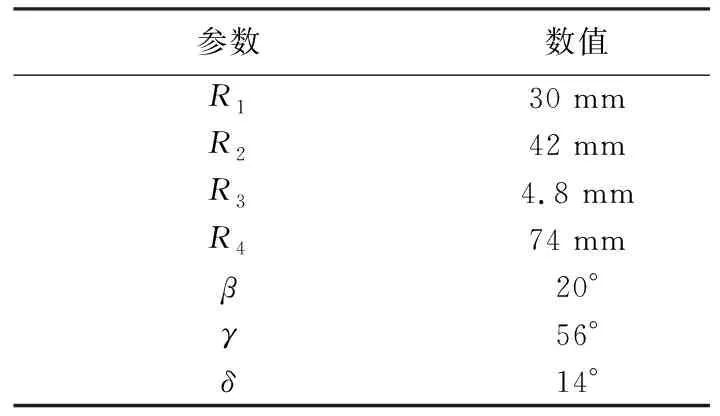
表1 隧洞与裂隙具体参数

表2 研究工况

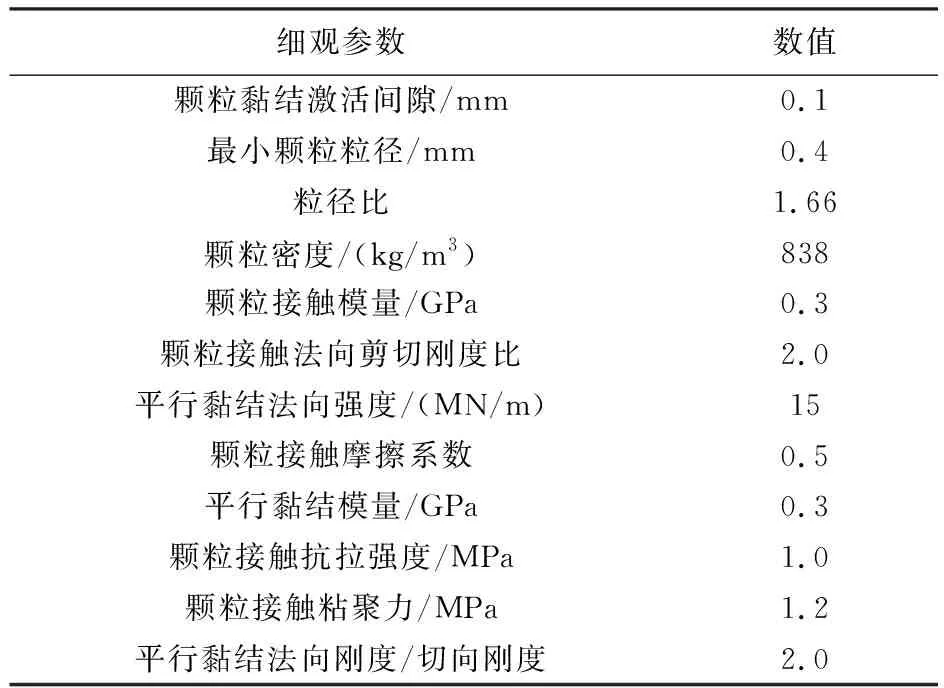
表3 类岩石材料的细观物理力学参数

2 研究结果与分析

2.1 裂隙长度对隧道围岩应力的影响

工程岩体中存在多组裂隙，其形态、数量及长度直接影响岩体强度。对于隧道工程，围岩强度(围岩级别)是隧道支护体系设计的主要标准。隧道开挖过程中，拱圈附近成为临空面，裂隙的分布直接影响围岩稳定性，而常见的围岩失稳类型主要为拱顶塌方。因此，研究拱顶附近裂隙分布对隧洞围岩的应力影响具有一定的实际意义。对于工况1，当隧洞岩体模型中存在水平裂隙，从隧道拱顶至模型顶面布设监测点(P1～P30)。如图3所示，随着轴向应力σ逐渐施加至0.5 MPa，裂隙侧壁(P9监测点)附近水平应力σxx出现第一峰值点，隧洞拱顶附近(P2监测点)水平应力出现第二峰值点，即拉应力最大，易发生拉裂破坏。其中，当裂隙长度为10 mm时，拱顶附近拉应力较大；当裂隙长度为50 mm时，裂隙侧壁附近拉应力达到最大。此外，隧道顶部垂直应力自模型顶部向下逐渐减小(图4)，传递至裂隙侧壁附近消散零。但随着裂隙长度减小，两个临空面之间垂直应力逐渐增大。

图3 模型水平应力分布特征(σ=0.5 MPa)

图4 模型垂直应力分布特征(σ=0.5 MPa)

由此可见，当外荷载一致时，研究体系中的水平应力存在一定平衡关系。实际工程中，隧道开挖破坏原有地层的应力平衡，张开裂隙上覆岩体自重应力为固定值。随着水平预裂隙长度增加，隧道拱顶围岩内部水平拉应力逐渐减小，裂隙侧壁岩体内部水平拉应力逐渐增加，并在拱圈附近一定限界(P4监测点)处水平拉应力近似恒定(各曲线交汇点)。

如图5，6所示，随着裂隙长度的逐渐增加，不同监测点的水平应力也随之发生变化，裂隙长度每增加5 mm，监测点P2的水平应力变化量逐渐增加(图5)，而监测点P9处水平应力变化量逐渐减小(图6)。由此可见，随着岩体中节理、裂隙的长度接近隧洞宽度，裂隙周围拉应力的增长幅度逐渐减小。因此，岩体中裂隙长度对隧道侧壁应力的影响为非正比关系。

图5 监测点P2处水平应力变化

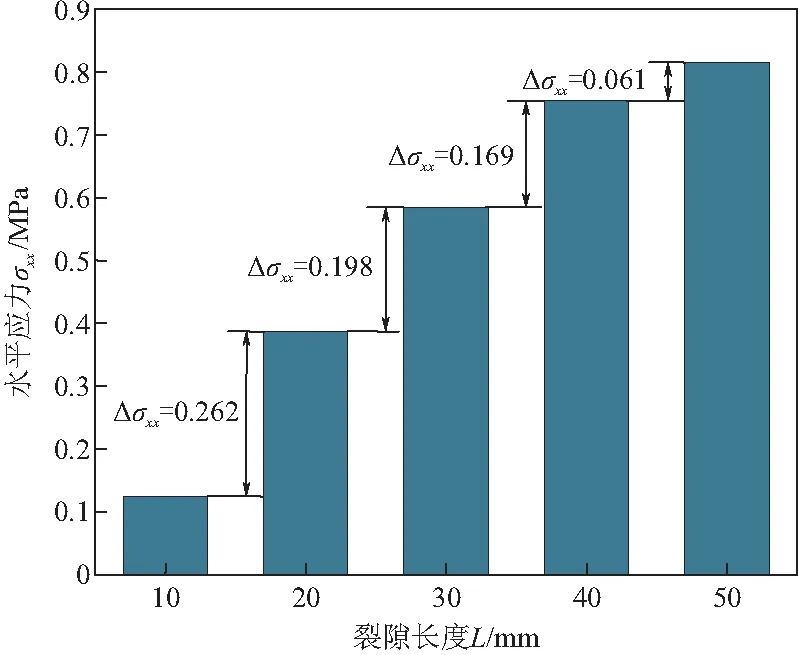
图6 监测点P9处水平应力变化

在定量分析的基础上，结合数值模拟应力链的分布特征，明显看出临空面处拉应力出现应力集中现象，并呈近似等边三角形分布(图7)。另外，裂隙至隧道顶部距离达到一定范围时，即两处拉应力区域交界点处(P4监测点)水平应力近似为恒定值。与此同时，裂隙尖端与隧道侧壁均出现压应力集中现象。

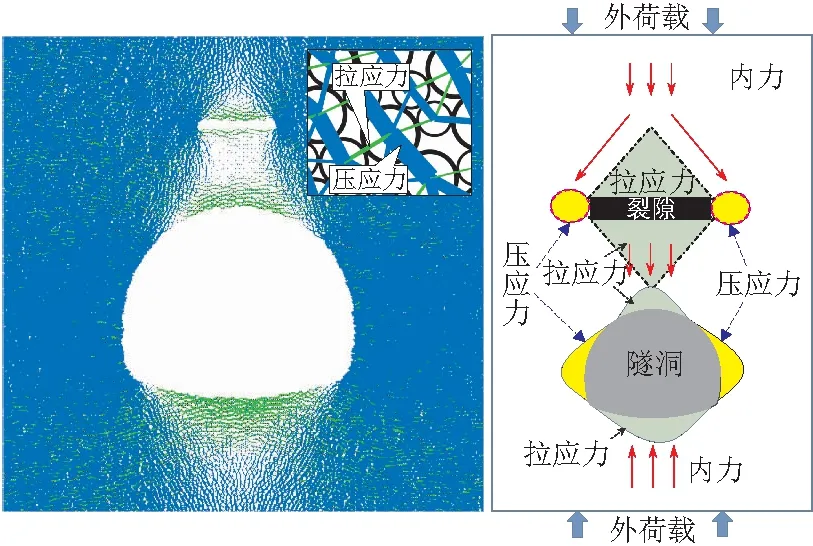
图7 模型中应力链分布特征

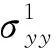
图8 垂直应力变化量与裂隙长度关系曲线

2.2 裂隙倾角对隧道围岩应力的影响

实际岩体中的节理裂隙并非水平分布，而呈多角度分布。为此，控制裂隙与隧道拱顶之间的距离为定值，研究裂隙角度对隧道侧壁围岩主应力的影响规律。如图9所示，拱顶与拱底位置最大主应力处于峰值，与应力分布状态(图7)一致，均易发生拉裂破坏。而拱圈侧壁最大主应力近乎为零，可见拉应力主要集中于隧道顶部与底部。因此，为探究拱顶、拱底最大主应力与裂隙倾角的相关性，进一步得到主应力与裂隙倾角的关系曲线(图10)。其中，隧道顶部与底部的拉应力均随着裂隙倾角的增大而增加，且增加幅度逐渐减小，底部拉应力均略大于顶部。然而，当裂隙倾角在20°～30°之间时，隧道拱顶与拱底处拉应力近似为恒定值。

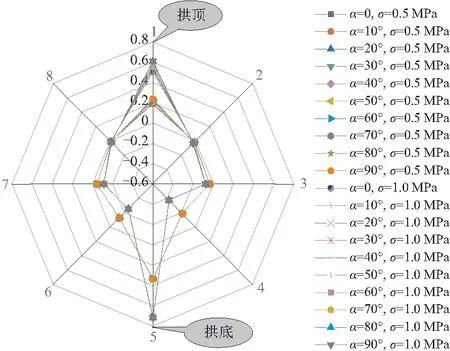
图9 隧道侧壁最大主应力分布

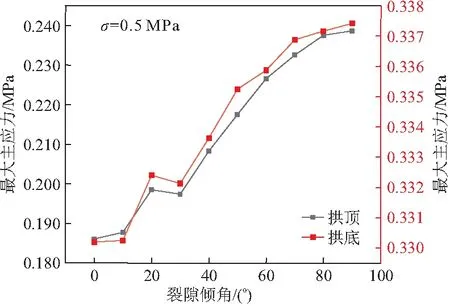
图10 隧道侧壁最大主应力与裂隙倾角关系曲线

进一步地，根据最小主应力分布特征(图11)，隧道拱肩、拱腰和拱脚附近的最小主应力绝对值较大。其中，拱腰附近压应力集中，随着裂隙倾角的增加，无显著变化，而左、右拱肩附近压应力变化较明显。如图12所示，随着裂隙倾角的增加，最小主应力绝对值均逐渐增加，即压应力增大，并在裂隙倾角20°～30°范围出现恒定值。综上所述，裂隙倾角的增加，使得拱顶围岩内部拉应力、拱肩及拱腰围岩内部压应力均增大，围岩的自稳能力减小。

图11 隧道侧壁最小主应力分布

图12 隧道侧壁最小主应力与裂隙倾角的相关性

裂隙对隧洞侧壁主应力影响的同时，也对研究模型整体破坏模式有一定的影响。如图13所示，当裂隙倾角在0～40°之间时，模型主要在隧道拱腰与模型底部之间形成贯通破裂面，呈“八”字形，并在模型右上方逐渐形成贯通裂纹，使得右拱肩处围岩压应力小于左拱肩(图12)。当裂隙倾角大于40°时，试验模型破裂方式主要沿模型对角分布。由此可知，裂隙倾角接近垂直时，对隧道周围的主应力影响逐渐减小，愈接近无裂隙状态。

图13 不同倾角的裂隙模型破坏特征

2.3 裂隙空间位置对隧道围岩应力的影响

图14 隧道侧壁最大主应力与裂隙位置的关系曲线

与此同时，在模型轴向应力σ增加过程中，拱肩位置围岩内部最小主应力变化规律一致(图15)，且不同裂隙位置对应最大主应力绝对值差值为近似恒定值(曲线接近重合)。由曲线分布特征可知，随着H的逐渐增加，拱肩围岩内部最小主应力绝对值出现先减小后增加。其中，当H值处于25 mm附近时，拱肩处围岩内部压应力最小。可见，当裂隙位于拱圈附近一定范围时，对隧道拱肩附近围岩受力越有利。

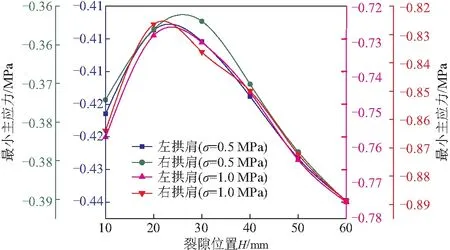
图15 隧道侧壁最小主应力与裂隙位置的关系曲线

结合模型应力链分布特征(图7)，裂隙侧壁与拱顶附近均形成拉应力三角区。如图16所示，隧道拱顶附近拉应力三角区高度为H1；裂隙侧壁拉应力三角区高度为H2。当裂隙位置H在20～30 mm之间时，上下三角拉应力区存在交点(H1+H2=H′)。由此可见，当拉应力区域出现或即将出现重合区时，模型拉应力重分布。故此，根据几何关系，存在以下关系式：

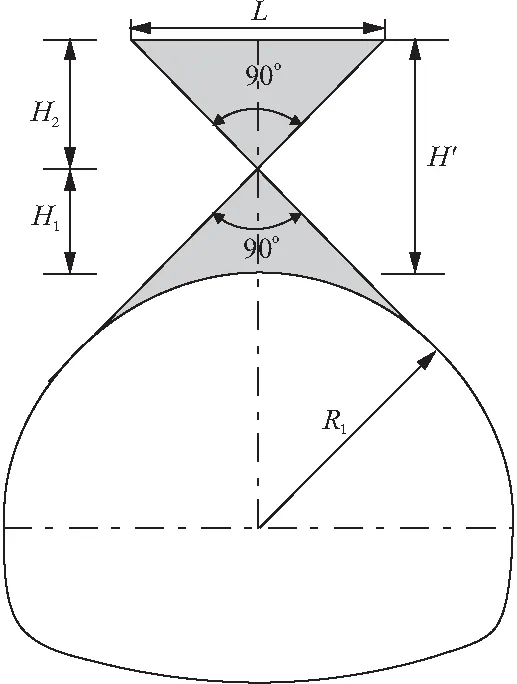
图16 模型拉应力分布示意

R1×(1/cos45°-1)+0.5×L=H′

(1)

进一步优化得到：

H′=0.414×R1+0.5×L,L≠0

(2)

实际隧道开挖过程中，若将拱圈附近的不利裂隙组进行注浆、加筋，则大幅度提高了拱圈围岩稳定性。如图17所示，结合围岩内部受力特征，可将隧道支护体系中系统锚杆最小长度设置为H′，以保证隧道安全。由式(2)可知，锚杆长度由两部分控制，一是隧洞拱圈半径R1，二是围岩中裂隙发育情况L。根据《公路隧道设计规范》表A.0.5～3.0[19]，实际岩体中张开裂隙的长度受上覆岩体自重应力的影响，并不会发育太长。当各组节理间距大于40 cm时，岩体处于节理不发育状态[19]。若按围岩节理发育与不发育界限控制，裂隙最大长度可取40 cm。此外，对于完整无裂隙的围岩(L趋近于零)，实际工程中隧道围岩等级较高，不需要打设系统锚杆，故式(2)中L应不等于零。对于两车道高速公路，隧道设计速度80 km/h，其内轮廓拱部半径一般为560 cm，开挖轮廓拱部半径约为640 cm(图17)，则系统锚杆长度约为2.85 m，其值在《规范》表 P.0.1[19]中给出系统锚杆长度范围2～3.5 m之内。因此，在实际隧道设计过程中，弥补了规范中系统锚杆长度范围太大的不足，可较为准确地得到系统锚杆长度。

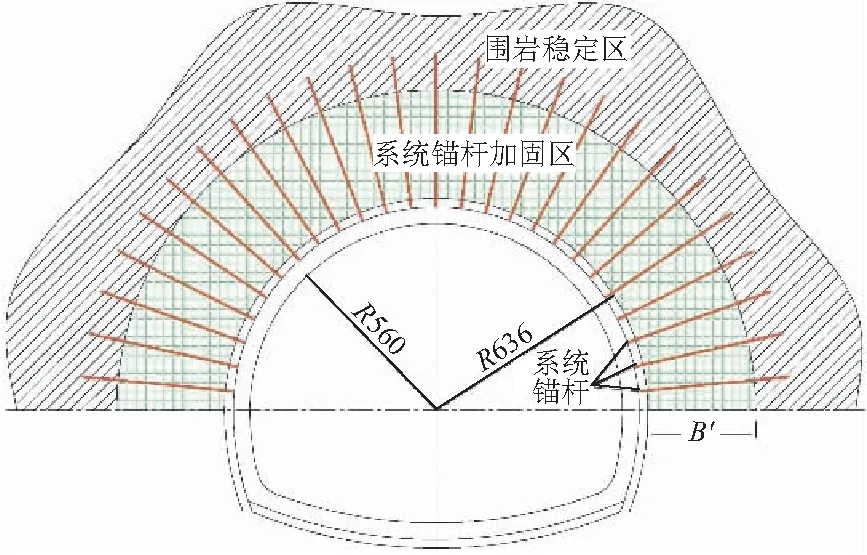
图17 隧道围岩系统锚杆加固范围

3 结 论

本文结合岩体力学理论，利用颗粒流数值模拟手段，由类岩材料的力学行为入手，从宏观与细观相结合的角度出发，详细分析了裂隙长度、倾角及空间位置对隧洞侧壁围岩应力的影响规律，得到了以下研究成果：

(1)随着水平预裂隙长度增加，隧道拱顶围岩内部水平拉应力逐渐减小，裂隙侧壁岩体内部水平拉应力逐渐增加，在拱圈附近一定限界(P4监测点)处水平拉应力近似恒定。而岩体中裂隙的长度越接近隧洞宽度时，裂隙周围拉应力的增长幅度逐渐减小。隧洞拱顶垂直应力随着隧道埋深的增大而增大，裂隙长度对其影响程度更大。

(2)裂隙倾角对隧道拱圈附近主应力影响较大。当裂隙倾角趋于90°时，拱顶与拱底围岩内部拉应力、拱肩附近压应力均逐渐增加，隧道围岩的自稳能力逐渐减小。此外，裂隙倾角在20°～30°之间时，隧道拱圈附近主应力近似不变，模型破坏模式近乎一致。

(3)裂隙空间分布位置与隧道拱圈围岩主应力存在较大的相关性。随着H值逐渐增加，拱顶围岩内部拉应力、拱肩围岩内部压应力均出现先减小后增加的变化规律，即隧道拱圈围岩主应力存在极值点。结合几何相似比关系，得出围岩待加固区宽度与裂隙长度、拱圈半径之间的相互关系。进一步得出隧道系统锚杆加固范围，较为准确的得到系统锚杆长度，对隧道穿越泥岩、板岩的设计、施工具有一定的指导意义。