基于改进遗传算法的结构静力响应区间分析

陈兴望， 龙晓鸿， 马永涛， 周群林， 桂石海

(华中科技大学 a. 土木与水利工程学院； b. 控制结构湖北省重点实验室， 湖北 武汉 430074)

传统结构分析与设计是基于确定性参数的，即分析设计过程中涉及的材料参数和荷载参数等都被视为确定的量值。然而，在工程各个阶段都存在一些不确定性信息，若将其简化为确定性信息处理，有时就会得出矛盾的或很不合理的结果[1]。所以为了让分析结果更加贴近工程实际，在工程结构分析和设计时必须考虑这些因素的不确定性。目前结构参数不确定性的描述方式主要有随机模型、区间模型和模糊模型。由于很多结构材料参数分布特征未知，但能确定大致分布范围，适合用区间模型描述。

按区间模型考虑结构不确定性时，可以使用不同的方法计算结构响应区间。有学者使用Monte Carlo Method(MCM)计算结构响应区间，并针对一般MCM的不足作了不同的改进[2～4]。MCM的解比较稳定，在抽样数量足够大的时候，计算得到的解能无限逼近甚至有可能达到精确解。但是MCM抽样效率较低，要得到比较精确的结果需要很大的计算量。Rao等[5]将静力问题表示为线性区间方程组，通过高斯消元法、顶点组合法和基于不等式的方法求解区间方程组，发现基于不等式的方法更为精确，但是随着自变量区间的增大会出现区间扩张的问题。这个问题可以通过区间截断来解决，吕震宙等[6]在此基础上提出了改进区间截断法，但区间截的标准难以设定，截断参数设置的主观性使计算结果的有效性难以评估。郭书祥等[7]提出了求解区间控制方程的迭代法，但当区间离差较大时，迭代不容易收敛[8]。有学者通过Chebyshev多项式[9]、径向基函数[10]和神经网络[11]等建立结构的替代模型，通过替代模型求解结构响应区间，但是对于静力问题来说，使用替代模型对计算速度的提高不明显，且替代模型还需要结合其他方法才能求解响应的区间。

有学者将智能优化算法用于结构响应区间的计算。Liu等[12]将贝叶斯算法运用到了结构不确定性分析中。汤剑[13]将遗传算法用于不确定性分析中。与传统法相比，智能优化算法在不确定性分析中展现出更高的效率和精度。然而，在结构响应分析中，需要计算的往往不是单个响应，而是要同时计算多个响应。但目前的遗传算法单次运行只能求解一个目标函数的最值，计算效率低。

智能优化算法的特点是迭代初期优化目标变化较大，而迭代中后期优化目标变化较小。因此若通过重复运行计算结构多个响应的区间，花费的计算时间与获得的计算精度不相称。针对这个问题，本文在传统遗传算法的基础上加入多个适应度函数，相应地改变了遗传操作方式，构建了能同时计算多个目标最优解的并行优化遗传算法(Genetic Algorithm for Parallel Optimization, GAPO)。最后使用GAPO计算桁架结构静力响应区间以验证算法的有效性。

1 遗传算法及其改进

1.1 遗传算法

遗传算法通过模拟生物进化中交叉、变异与自然选择，逐代淘汰适应度较低的个体，并由适应度较高的个体遗传产生下一代种群，使种群适应度逐渐收敛到最优值。遗传算法没有函数可导性和连续性的限制，并且具有较好的全局寻优能力，其核心内容为参数编码、初始种群的生成、适应度函数设计、遗传方式设计以及迭代控制方式设计。遗传算法的计算流程及本文中各部分的处理方式如图1所示。

图1 遗传算法计算流程

1.2 并行优化遗传算法

传统遗传算法只能进行单个适应度函数的优化计算，而后续分析需要对多个神经网络进行优化，所以使用传统遗传算法进行结构响应分析会使计算量非常大，计算效率低。为此，本文在传统遗传算法的基础上进行改进，提出并行优化遗传算法(GAPO)，同时进行多个神经网络的超参数优化。

值得注意的是，提出的并行优化遗传算法与多目标优化遗传算法(Multi-objective Genetic Algorithm，MOGA)不同。两个算法的共同点是都可能有多个适应度函数，但MOGA算法是寻找每个适应度尽量高的某一个个体，即适应度整体较高，但单个适应度不一定达到最优。而本文提出的GAPO算法是分别寻找每个适应度达到最优时对应的个体，相当于把多次优化分析整合为一次优化分析以提升计算效率。

(1)

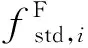
(2)

式中：NFF为适应度函数的个数；nsvv为每个适应度下存活的个体个数；α为考虑计算量的调整系数;cmut为种群变异率。包含两个适应度函数的遗传算法遗传，操作如图2所示。

图2 两适应度GAPO遗传操作示意

2 基于GAPO的结构静力响应区间计算方法

R=f(x1-x2-…-xm)

(3)

其中R={Ri},i=1,2,…,n为要求的n个结构响应组成的向量。该函数以GAPO中个体基因序列为输入，提取其中的结构参数取值，将结构中的区间变量取为该组确定的值，计算并输出需要的结构响应。求结构响应的区间此时转化为求函数的值域。

GAPO与其他优化算法一样，默认求各目标函数的最小值，所以求解区间需要分两次分别求解最大值和最小值，且适应度函数值越低，适应度越高。当求各响应最小值时，各适应度函数取为

(4)

各最佳适应度函数值即为各响应最小值。而求解响应最大值时，适应度函数取为

(5)

各最佳适应度函数值的相反数为响应最大值。

对于容易写出控制方程的结构体系，响应计算函数提取结构参数后可直接计算刚度矩阵和荷载列阵，进而得到结构响应列阵。而对于比较复杂或有较强非线性的结构，其控制方程的求解需要比较复杂的迭代，使用编程实现比较困难，此时结构响应的计算可以通过有限元程序实现。考虑到计算速度和程序交互的需求，本文使用OpenSees进行结构的建模和计算，使用tcl命令流编写结构建模、分析和结果输出的文件。编写文本文件修改程序，MATLAB结构响应计算函数提取区间参数的取值后，使用文本文件修改程序将tcl命令流中结构参数取值修改为当前抽样的取值，在响应计算函数中调用OpenSees程序运行命令流文件计算并输出结果文件，再读取结果文件中需要的结构响应并输出。此时结构响应计算函数如图3所示。

图3 结构响应计算函数

3 算 例

文献[5]中介绍的平面桁架结构，如图 4所示。该桁架由10根杆组成，在结点2和结点4分别受到竖直向下的力FP=100 N。桁架根据最小自重原则设计，各杆的横截面积不同。各杆弹性模量均为E=107N/mm2，横截面积以及不考虑结构不确定性时的轴应力见表1。当各杆件横截面积存在1%的波动时，求各杆轴应力的区间。

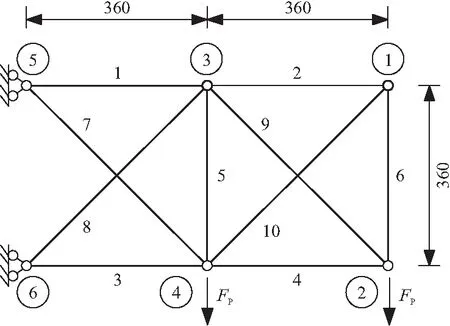
图4 10杆桁架/mm

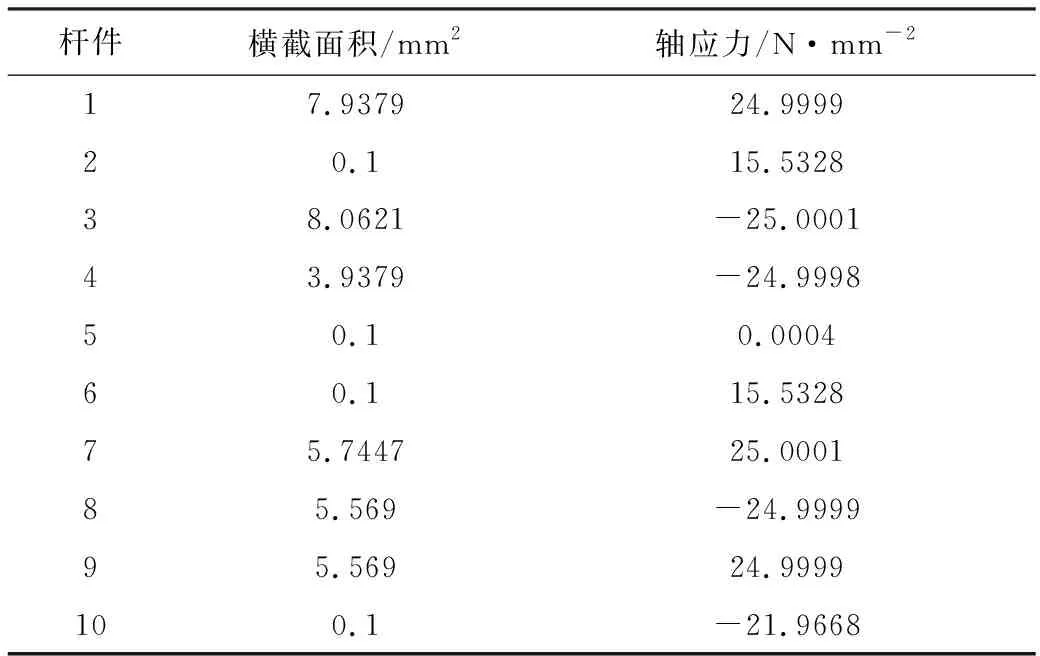
表1 桁架的设计横截面积和轴应力

文献[5]中提出了解区间有限元控制方程组的截断法，并与顶点组合法的计算结果进行了对比。本文用样本数量为100000的MCM和GAPO算法分别对桁架轴应力区间进行计算，种群数量设置为300，存活率为2%，交叉率0.8，变异率0.2，最大迭代次数为30。截断法(截断参数t=0.01，0.1)[5]、顶点组合法[5]、MCM以及GAPO对桁架杆件轴应力上下限计算结果见表 2，各方法计算结果对比如图5。

表2 杆件轴应力区间计算结果 N·mm-2

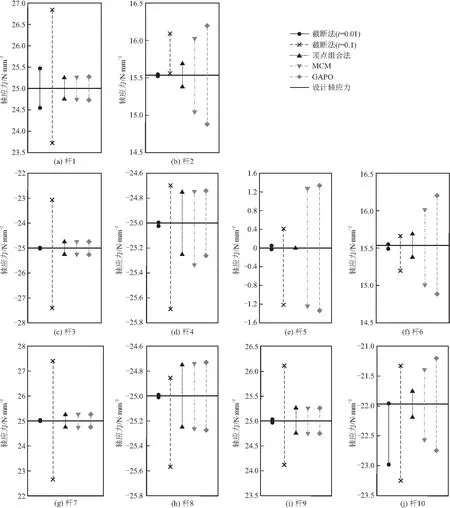
图5 不同方法计算的杆件轴应力区间

由于MCM计算结果较为稳定和可靠，主要将其他方法计算结果与MCM计算结果进行比较。由表中数据和对比图可见，截断法计算结果极不稳定，截断系数t对计算结果的影响很大，但要确定合适的截断系数比较困难。顶点组合法对一部分构件的轴应力计算可以得到比较精确的结果，但由于没有考虑结构响应在区间中的非单调性，可能会低估某些杆件轴应力的范围。由图可见GAPO计算结果的稳定性不亚于MCM，并且用GAPO计算的每根杆件轴应力区间都稍大于MCM(即GAPO计算的上限大于MCM计算的上限，GAPO计算的下限小于MCM计算的下限)。由于GAPO和MCM本质上都是抽样的方法，计算结果只会趋近于精确解，而不会超越精确解，则可知GAPO精度高于MCM。

计算量方面，MCM进行了100000次静力分析，而GAPO轴应力下限和上限计算分别迭代了30次，即一共进行了(30+1)×2×300=19200次静力分析，计算量远小于MCM。而对于一般遗传算法，即使将种群数量设为100，最大迭代次数设为20，由于每次只能进行1个适应度的优化计算，要得到10根杆的轴应力区间也要进行 (20+1)×20×100=42000次静力分析。所以对于多适应度问题，特别是多个适应度是同一次计算的多个输出的时候，GAPO在计算量方面比一般遗传算法更有优势。

4 结 论

本文以区间变量描述结构参数的不确定性，考虑同时求解多个结构响应最值的需求，在传统遗传算法的基础上加入多个适应度，改变了遗传操作机制，构建了可以同时对多个适应度进行优化分析的GAPO算法，并使用GAPO计算结构静力响应区间。经过算例测试发现，GAPO比区间截断法和顶点组合法更稳定，能通过远小于MCM的计算量，得到更精确的结果，且在计算量方面比传统遗传算法也更有优势。此外，此方法也适用于结构动力响应问题，即在结构响应计算函数中计算结构的动力响应并返回需要的响应值。