连续配筋混凝土复合式沥青路面Top-Down裂缝疲劳扩展研究

2023-01-18李盛余时清张豪王阳

中南大学学报（自然科学版） 2022年11期

李盛，余时清，张豪，王阳

(1.长沙理工大学交通运输工程学院，湖南长沙，410114；2.中冶南方城市建设工程技术有限公司，湖北武汉，430063)

连续配筋混凝土刚柔复合式路面(CRC+AC)是由高强度的刚性基层与柔性的沥青混凝土面层进行复合的一种路面，其中，CRC(continuously reinforced concrete)层作为承重结构层，AC(asphalt concrete)层作为表面功能层，可以提高路面的行车舒适性，降低CRC 层中的荷载及温度疲劳应力，减小雨水对基层和钢筋的损害。该复合式路面结构具有行车舒适性好、使用寿命长、整体强度高、维修费用小等众多优点，长期来看，经济性也很好，是我国重载交通和严酷气候环境下耐久性路面的主要结构形式之一[1-4]。近年来，Top-Down裂缝已被国内外道路工程界广泛关注，Top-Down 开裂是沥青路面多种病害的重要诱因，严重影响路面的行驶质量和行车安全[5-10]。有限元方法(finite element method)是目前模拟工程实际问题应用最广泛的一种方法，但在求解裂缝开裂扩展问题时存在一定缺陷。传统有限元应用于裂缝开裂扩展分析时，需要对裂缝区域进行一定程度的细化，且裂缝每扩展一步就需要重新划分网格，计算工作量大大增加。其次，传统有限元要求裂缝扩展路径只能沿着单元边界扩展，不能穿过单元内部，大大降低了计算精度。针对传统有限元方法分析裂缝开裂扩展问题的不足，为了解决传统有限元理论的许多局限性，BELYTSCHKO等[11]提出了扩展有限元方法(extended finite element method,XFEM)，其主要理论是根据传统的有限元方法对连续区域进行处理，修改后的位移函数用于表征不连续区域，且介绍了一种描述不连续边界条件的方法。SUKUMAR 等[12]模拟了三维裂缝静态问题，在XFEM 中，引入了不连续函数和渐近函数来表征裂缝界面处的内部位移场和裂缝尖端前部的位移场。STOLARSKA 等[13]将水平集方法引入到XFEM 方法中，并利用XFEM 理论计算裂缝扩展过程中的位移场和应力场。LARSSON等[14]将材料力学应用于XFEM的运动学方程中，使得XFEM中的连续位移和不连续位移彼此独立，从而不需要在裂缝扩展模拟中更改裂缝位置。HOSSEINI等[15]发现采用扩展有限元方法可以大大减少裂缝尖端的网格数量并避免网格的重建，并且由此获得的混合裂缝扩展模拟结果与实验结果非常吻合。

余天堂等[16-18]通过研究获得了一种求解不连续函数的积分方法，并用其计算裂缝尖端的应力强度因子。王新飞[19]通过对沥青砂浆裂缝扩展过程进行模拟，发现了骨料对扩展路径的影响特征。杜效鹄等[20-21]利用局部富集函数表示混凝土的开裂面积，并模拟了混凝土梁在剪切作用下的断裂过程以及凝结过程中黏结裂缝的扩展，证明了该方法的有效性。杨擎[22]通过分析交通荷载作用下沥青路面的裂缝扩展路径，研究不同因素对多裂缝扩展路径的影响，包括轮载作用位置、多裂缝干涉效应、面层模量和面层厚度等。甄西刚[23]研究了温度作用下沥青路面的裂缝扩展，并发现了温度场对裂缝扩展的影响特征。

国内外学者对扩展有限元理论和应用进行了大量研究，但未见扩展有限元方法在复合式路面Top-Down 开裂方面的应用研究，为此，本文作者通过有限元数值模拟，并结合实体工程的调研成果，分析温缩应力-交通荷载作用下Top-Down 裂缝疲劳扩展特性。研究成果可为CRC+AC 复合式路面的结构设计和沥青面层开裂分析提供理论依据，并促进CRC+AC复合式路面的推广应用。

1 裂缝疲劳扩展相关理论

1.1 线弹性断裂力学理论

线弹性断裂力学的基本理论来源于弹性力学理论，根据裂缝尖端区域的应力场和位移场分析裂缝的稳定性。裂缝根据荷载作用的形式不同，可分为张开型裂缝(Ⅰ型)、滑开型裂缝(Ⅱ型)、撕开型裂缝(Ⅲ型)共3 种基本类型。在线弹性力学中，应力强度因子K通常用于描述裂缝尖端的应力、应变场，其计算式为

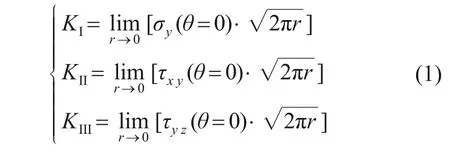
式中：KI，KⅡ和KⅢ分别为I型，Ⅱ型，Ⅲ型裂缝尖端的应力强度因子；θ和r为以裂缝顶点为原点的极坐标。

应力强度因子K是衡量是否开裂的定量指标，当裂缝尖端的应力强度因子K达到临界值KIC时，裂缝会发生失稳性扩展，这称为K准则。

通过研究玻璃材料的脆断问题，从能量平衡的角度确立了裂缝扩展准则[24]。能量释放率G与裂缝的长度、形状和位置有关。对于I型裂缝，其能量释放率用GⅠ表示，能量释放率临界值用GⅠC表示。当能量释放率GⅠ小于临界值GⅠC时，裂缝不会扩展；若GⅠ大于或等于GⅠC，则裂缝就会发生失稳扩展。这称为G准则。

K准则和G准则存在如下转换关系：

式中：E为弹性模量；ν为泊松比。

1.2 疲劳裂缝扩展准则

单位循环荷载下裂缝扩展的长度用da/dN表示，其中，da表示裂缝扩展深度，dN表示荷载循环次数。大量试验表明，da/dN与应力强度因子变化幅值ΔK=Kmax-Kmin有一定的关系。其中，Kmax和Kmin分别为最大应力强度因子和最小应力强度因子。在断裂力学中，断裂能释放率G与应力强度因子K一样，是用来描述裂缝扩展原动力的指标[25]。

将传统的Paris 公式中的应力强度因子K替换成断裂能释放率G，用断裂能释放率G表示的改进型Paris公式描述裂缝疲劳扩展的各个阶段，如图1所示。

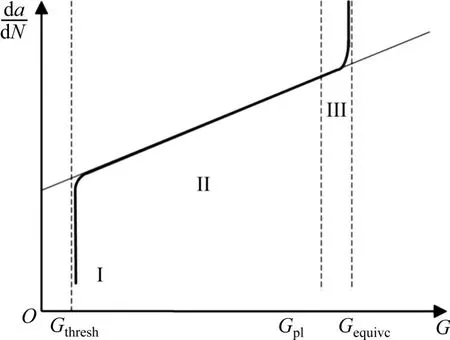
图1 改进型Paris公式曲线Fig.1 Improved Paris formula curve

图1 中，Gthresh为断裂能释放率阈值，只有当裂缝尖端的断裂能释放率超过该值时，裂缝才开始扩展；Gpl为断裂能释放率上限值，即当断裂能释放率超过该值时，疲劳裂缝扩展进入到图1所示的第Ⅲ阶段；Gequivc为材料的极限断裂能释放率，即材料的断裂韧度。裂缝扩展需要满足以下关系式：

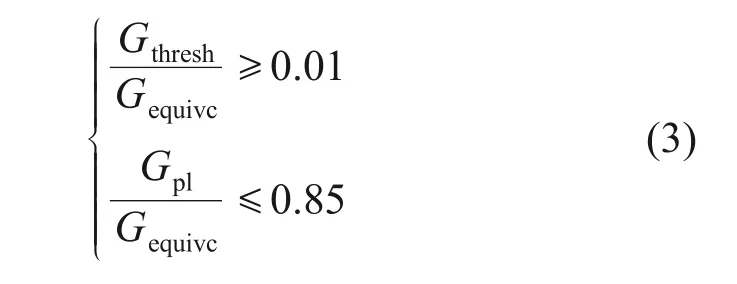
裂缝扩展分为3个阶段。

第Ⅰ阶段：当ΔG≤Gthresh时，裂缝不发生扩展。

第Ⅱ阶段：当Gthresh＜ΔG≤Gpl时，裂缝处于稳定扩展阶段。在该区内，一般认为Paris 公式符合模拟混合料裂缝扩展的情况，Paris 裂缝扩展公式为

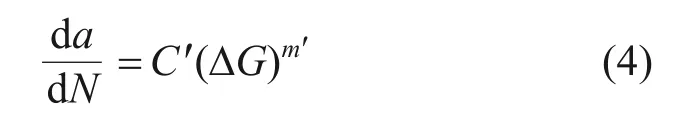
式中：C′和m′为改进型Paris 公式中与材料相关的参数；ΔG为最大交变应力和最小交变应力下断裂能释放率之差，即ΔG=Gmax-Gmin，其中，Gmax为最大交变应力下断裂能释放率，Gmin为最小交变应力下断裂能释放率。

第Ⅲ阶段：ΔG≤Gpl，裂缝处于失稳扩展阶段。此阶段裂缝扩展速度较快，疲劳寿命较短可忽略不计。

2 温缩应力作用下沥青面层Top-Down裂缝疲劳扩展

2.1 沥青面层温缩应力计算模型

路面结构层的温度随着气温的降低而降低，使结构层内部产生收缩变形。路面结构属于带状构造物，其纵向的长度较大，因此降温时，路面结构主要表现为纵向收缩变形，致使路面产生横向裂缝。

对扩展有限元模块进行疲劳分析时用到的分析步类型是直接循环类型，模型长度×深度为10 m×8 m，温度场采用的是冬季低温季节5:00 时路面结构温度场。根据北京足尺路面试验环道实测的气象资料，选择2018 年1 月11 日为冬季低温天气的代表日，其外部气象参数如表1所示。

表1 2018年1月11日北京市气象参数Table 1 Meteorological parameters of Beijing on January 11,2018

为了对沥青路面温度场进行模拟，需要以沥青路面各结构层材料的热物性参数为基础对有限元模型的温度进行计算。路面各结构层材料的热力学参数如表2所示。

表2 路面材料热力学参数Table 2 Thermal physical parameters of pavement materials

图2 所示为降温之后沥青层内部温度场分布，图3 所示为路面深度与温缩应力的拟合曲线。在Abaqus 荷载模块中，可将上述温度与应力的关系以函数表达式表征。

图2 沥青层内部温缩应力Fig.2 Internal temperature stress of asphalt layer

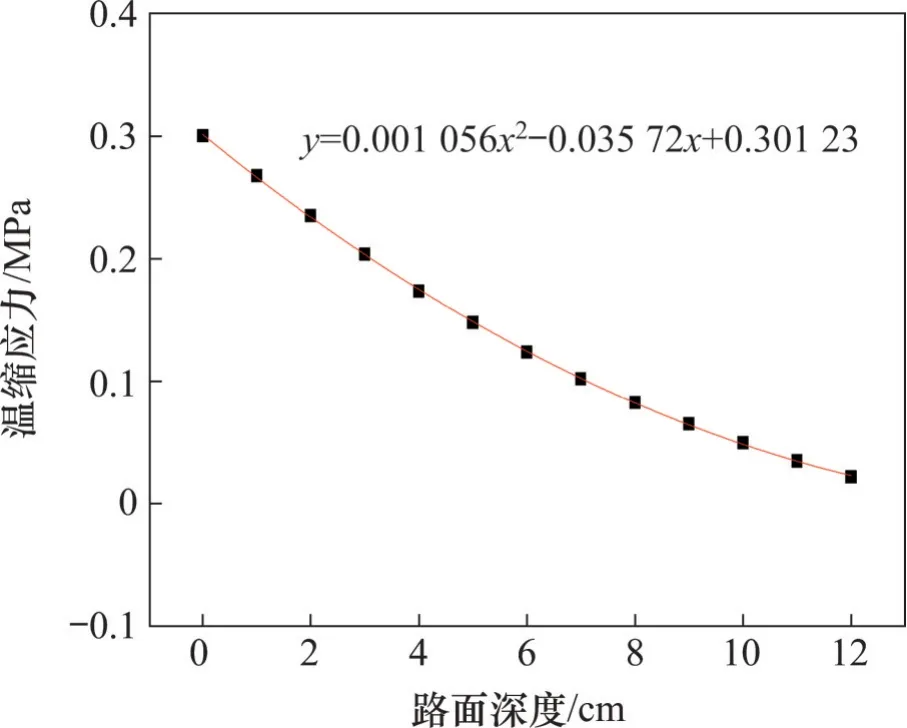
图3 沿路面深度方向温缩应力拟合曲线Fig.3 Fitting curve of temperature stress along depth of road surface

2.2 路面结构材料参数

为了简化运算并实现温缩型Top-Down 裂缝的自动扩展，对模型进行如下假定：

1) 各层均由各向同性、均质的材料组成，各层材料本构模型均为线弹性模型，层间接触完全连续。

2) 在路表中心已经出现深度为10 mm 的初始裂缝。

3) 温缩应力以体力的形式施加，且只作用在沥青面层。

通过半圆弯曲试验得到AC-20 沥青混合料的疲劳参数，见表3。

表3 沥青混合料AC-20的疲劳断裂参数Table 3 Fatigue fracture parameters of asphalt mixture AC-20

路面结构有限元模型长度方向为10 m，深度方向为8 m，其他参数如表4 所示。路面结构受力如图4所示。

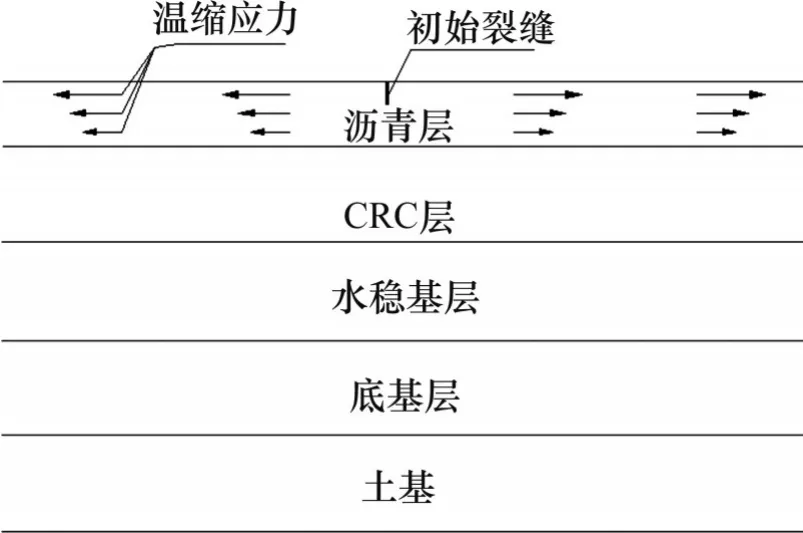
图4 路面结构受力示意图Fig.4 Schematic diagram of pavement structure stress

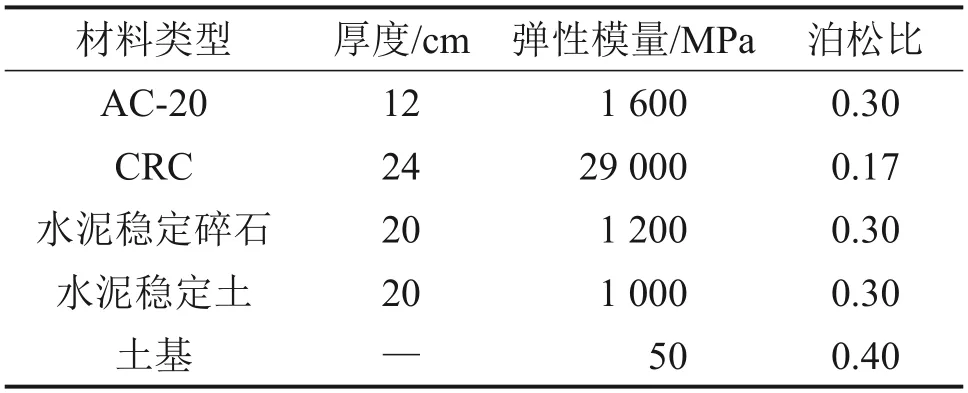
表4 路面结构层材料参数Table 4 Material parameters of pavement structure layer

2.3 温缩型Top-Down裂缝疲劳寿命分析

通过Abaqus 中的关键字输入ENRRTXFEM 命令可在结果中输出断裂能释放率，得到整个Top-Down裂缝扩展阶段裂缝尖端的断裂能释放率变化情况，如图5所示。

由图5可知：裂缝尖端的断裂能释放率随着裂缝扩展深度的增加先增加后减小，这是因为随着裂缝扩展，温缩应力循环次数增加使得能量释放率逐渐增加；当裂缝扩展到10 cm后，裂缝逐渐接近CRC 层，虽然沥青层厚度越来越小，但由于模型呈完全连续状态，使得CRC 层抵抗裂缝扩展能力越来越强。当裂缝深度为1 cm 时，裂缝尖端的断裂能释放率为42.3 N/m，而疲劳裂缝扩展的阈值Gthresh为极限断裂能的0.01倍，即9 N/m，初始断裂能释放率大于阈值，因此，Top-Down 裂缝从预裂缝深度为1 cm 时开始扩展并直接进入中速稳定扩展阶段，也就是裂缝扩展进入改进型Paris 公式曲线的第Ⅱ阶段。当裂缝深度扩展到10.5 cm 时，断裂能释放率达到最大值190.3 N/m，但远没有达到进入第Ⅲ阶段也就是疲劳裂缝失稳扩展阶段时断裂能释放率上限值，即900 N/m×0.85=765 N/m，因此，Top-Down裂缝只在第Ⅱ阶段进行扩展。

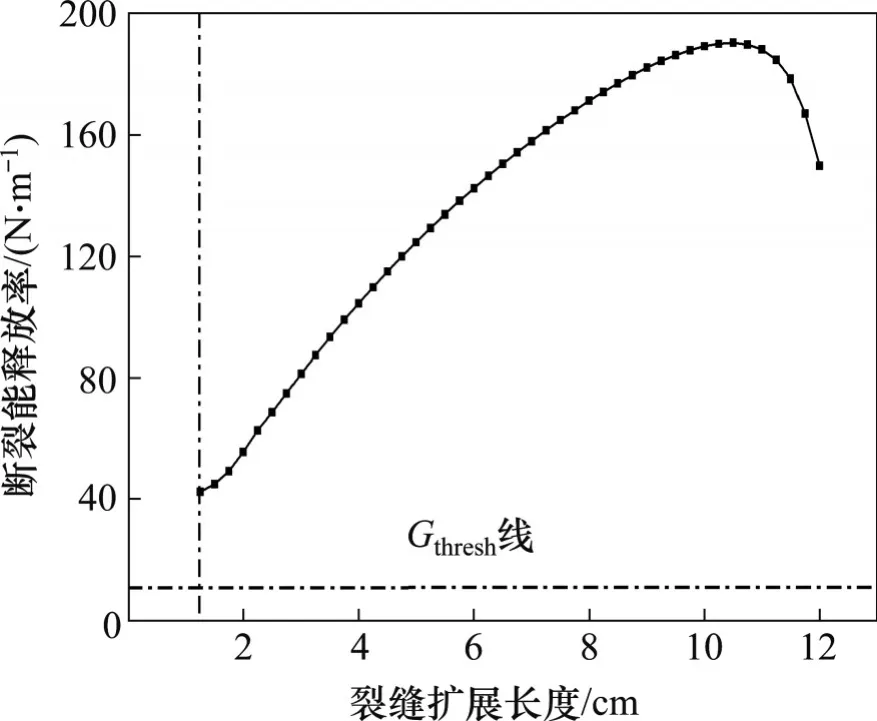
图5 断裂能释放率随裂缝扩展深度变化Fig.5 Fracture energy release rate varies with crack propagation length

根据所建疲劳扩展模型计算出温缩应力循环作用下Top-Down裂缝扩展深度随温缩应力循环次数的变化，如图6所示。

图6 裂缝扩展深度随温缩应力循环次数的变化Fig.6 Crack propagation length varies with number of temperature shrinkage stress cycles

由图6 可知：Top-Down 裂缝从初始裂缝1 cm深扩展到沥青层底部的荷载作用次数为34 142次。总体来看，断裂能释放率随着裂缝扩展深度增加而增大，Top-Down 裂缝扩展在后期呈加快趋势，所以，Top-Down 裂缝疲劳寿命在整个面层深度方向存在差异。当Top-Down 裂缝在面层上部扩展时，因为断裂能释放率较小，面层上部疲劳寿命较长。将12 cm厚的面层平均分为上下2层，厚度为6 cm，其疲劳寿命占比如表5所示。

表5 沥青面层疲劳寿命占比分析Table 5 Fatigue life ratio analysis of asphalt surface course

由表5 可知：上1/2 层沥青面层疲劳寿命为整个沥青面层Top-Down 裂缝疲劳寿命的53.8%，下1/2 层沥青面层疲劳寿命约为整个沥青面层Top-Down裂缝疲劳寿命的46.2%。上1/2层沥青面层疲劳寿命约为下1/2层的1.2倍。

2.4 温缩型Top-Down裂缝疲劳寿命影响因素

2.4.1 沥青层模量

为研究沥青层模量对Top-Down裂缝疲劳扩展影响，计算模型及其他参数不变，只改变沥青层模量，分别取1 200，1 400，1 600，1 800和2 000 MPa，分析Top-Down 裂缝的扩展及其疲劳寿命情况，裂缝尖端断裂能释放率变化规律如图7所示。

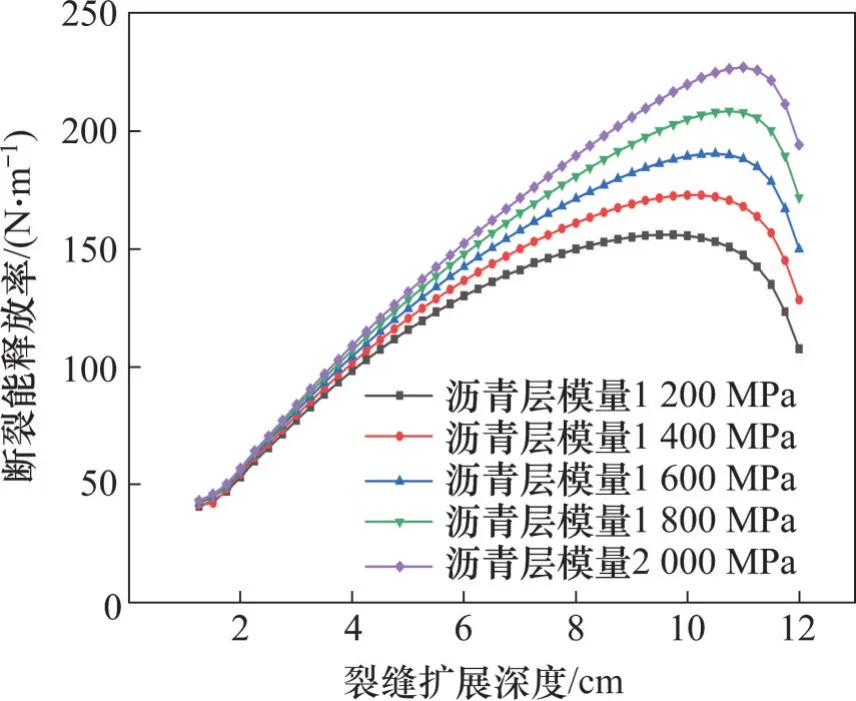
图7 不同沥青层模量下断裂能释放率随裂缝扩展深度的变化Fig.7 Variation of fracture energy release rate with crack extension length for different asphalt layer modulus

由图7 可知：沥青层模量的改变使Top-Down裂缝尖端断裂能释放率达到最大值时对应的裂缝扩展深度发生改变，即沥青层模量越大，Top-Down裂缝尖端断裂能释放率达到最大值时，其对应的裂缝扩展深度越大。如当沥青层模量为1 200 MPa 时，Top-Down 裂缝尖端达到断裂能释放率上限值时的裂缝深度为9.75 cm；当沥青层模量为2 000 MPa，Top-Down 裂缝尖端达到断裂能释放率上限值时的裂缝深度为11.00 cm。通过建模分析，获得沥青层模量变化时的沥青面层Top-Down裂缝疲劳寿命变化规律，如图8所示。

图8 裂缝扩展深度随温缩应力循环次数的变化Fig.8 Variation of crack extension length with number of temperature shrinkage stress cycles

由图8 可知：随着沥青层模量增加，Top-Down 裂缝疲劳寿命逐渐减小；当沥青层模量从1 200 MPa 增加到2 000 MPa 时，Top-Down 裂缝从初始深度1 cm 扩展到沥青层底部时温缩应力的循环数从35 888次减小到32 292次，减小了10.02%。因此，适当减小沥青层模量可以有效地减缓Top-Down裂缝在沥青面层内部的疲劳扩展速率，增大Top-Down 裂缝疲劳扩展寿命，延长路面使用年限。

2.4.2 沥青层厚度

为研究沥青层厚度对Top-Down 裂缝疲劳扩展的影响，计算模型及其他参数不变，只改变沥青层厚度hAC，hAC分别取8，10，12，14 和16 cm，分析Top-Down裂缝的扩展及其疲劳寿命。裂缝尖端断裂能释放率变化规律如图9所示。

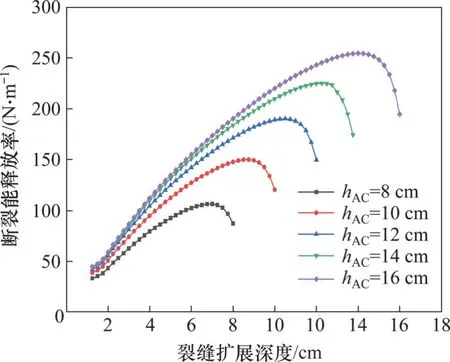
图9 不同沥青层厚度hAC下断裂能释放率随裂缝扩展深度的变化Fig.9 Variation of fracture energy release rate with crack extension length for different asphalt layer thicknesses

由图9 可知：当初始裂缝深度为1 cm 时，不同沥青层厚度下沥青层Top-Down裂缝的初始断裂能释放率不同，沥青层厚度越大，初始裂缝尖端断裂能释放率越大；沥青层厚度的改变会导致裂缝尖端的断裂能释放率发生变化；随着沥青层厚度的增加，Top-Down 裂缝尖端的断裂能释放率逐渐增加，当沥青层厚度从8 cm 增加到16 cm 时，Top-Down 裂缝尖端的断裂能释放率最大值从106.4 N/m 增加到254.5 N/m，增加了139.2%，但沥青层模量对Top-Down裂缝尖端的断裂能释放率变化规律基本没有影响。

通过数值模拟分析，获得沥青层厚度变化时的沥青面层Top-Down裂缝扩展深度变化规律，如图10所示。

图10 不同沥青层厚度hAC下裂缝扩展深度随温缩应力循环次数的变化Fig.10 Variation of crack extension length with number of temperature shrinkage stress cycles for different asphalt layer thicknesses

由图10 可知：随着沥青层厚度增加，Top-Down 裂缝贯穿沥青层时所经受的温缩应力循环次数增大；当沥青层厚度从8 cm 增加到16 cm时，Top-Down裂缝从初始深度1 cm扩展到沥青层底部时温度应力的循环次数从27 422 次增加到41 495次，增加了51.32%。但每厘米厚度的沥青面层Top-Down 裂缝平均疲劳寿命从3 428 次减小到2 593 次，减少了24.4%。由此可以得出增加沥青层厚度并不能增加单位沥青厚度的疲劳寿命，而是改变了裂缝尖端受力情况。综上所述，适当增加沥青层厚度可以减小Top-Down裂缝在沥青面层内部的疲劳扩展速率，延长沥青面层的服役寿命。

3 温缩-荷载耦合作用下沥青面层Top-Down裂缝疲劳扩展

3.1 荷载作用下Top-Down裂缝疲劳扩展分析

3.1.1 模型的建立

交通荷载作用在Top-Down 裂缝处时，主要有2种位置：一种是在裂缝中心上方，一种在裂缝中心一侧。其中最不利的位置为裂缝一侧，因此，将交通荷载设置在裂缝中心的一侧。对荷载型Top-Down 裂缝扩展进行模拟时，在路表中心处设置初始Top-Down裂缝，交通荷载作用在裂缝中心一侧，交通荷载简化为直径等于0.213 m的圆形荷载。对路面结构简化为二维模型分析时，其荷载不适用常规的静力等效原则转换，取交通荷载为标准轴载100 kN。

3.1.2 荷载作用下Top-Down裂缝疲劳扩展分析

根据模拟结果，单一车辆荷载疲劳作用并不能使Top-Down 裂缝发生扩展，为使裂缝发生扩展，可增加车辆荷载和增大初始裂缝深度，得到断裂能释放率的变化情况。图11和图12所示分别为不同车辆荷载和不同初始裂缝深度下断裂能释放率的变化情况。

图11 车辆荷载变化对断裂能释放率的影响Fig.11 Effect of vehicle load on fracture energy release rate

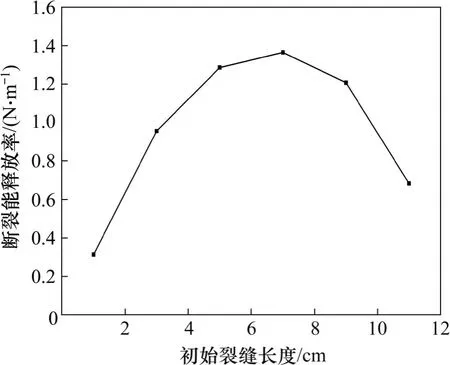
图12 初始裂缝深度对断裂能释放率的影响Fig.12 Effect of initial crack length on fracture energy release rate

由图11 和图12 可知：在车辆荷载作用下，随着车辆荷载的增加，Top-Down 裂缝尖端断裂能释放率也会随之增加，但最大值只有1.25 N/m，远小于疲劳裂缝扩展阀值9.00 N/m；而随着初始裂缝深度的增加，Top-Down 裂缝尖端断裂能释放率呈现出先增加后减小的变化规律，其最大值为1.37 N/m，远小于疲劳裂缝扩展阀值9.00 N/m。因此，在扩展有限元中，对于Top-Down裂缝，仅仅施加车辆荷载远不能使其发生疲劳扩展。

3.2 温缩-荷载耦合作用下Top-Down 裂缝有限元建模

在对温缩作用下Top-Down 裂缝分析结果的基础上，建立沥青面层温缩应力和交通荷载耦合作用下Top-Down裂缝疲劳扩展的模型，在路表初始裂缝中心一侧施加交通荷载，交通荷载与3.1.1 节中的相同，路面结构、材料参数以及温缩应力分布等参数与2.1 节和2.2 节中所述参数相同，Top-Down 裂缝预设裂缝深度为1 cm。沥青面层温缩-荷载耦合作用下Top-Down裂缝疲劳扩展加载示意如图13所示。

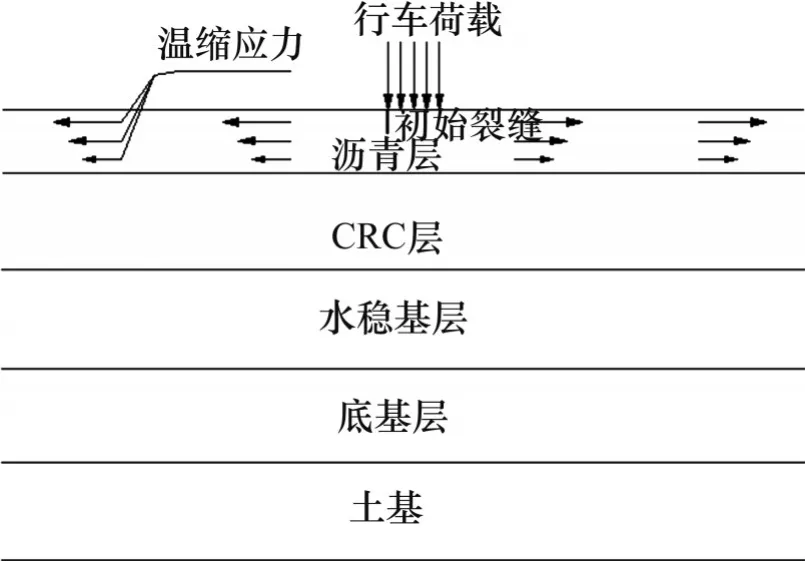
图13 温缩-荷载耦合作用示意图Fig.13 Schematic diagram of temperature shrinkage-load coupling

3.3 温缩-荷载耦合作用下Top-Down 裂缝疲劳扩展分析

基于XFEM 方法和改进型Paris 公式的裂缝疲劳扩展模型，沥青面层温缩应力和交通荷载耦合作用下Top-Down 裂缝从1 cm 扩展到12 cm 时的扩展情况如图14～18所示。

由图14～18可得：在面层温缩应力和交通荷载耦合作用下，Top-Down 裂缝发生复合型扩展；在耦合荷载的循环作用下，Top-Down 裂缝裂缝尖端能够自由地穿过纵向和横向单元内部，已经扩展的单元自动断开，并在后续扩展中保持断开状态。

图14 N=1次，a=1 cm时的裂缝扩展图Fig.14 Crack propagation diagram when N is 1 times and a is 1 cm

图15 N=8 382次，a=3 cm时的裂缝扩展图Fig.15 Crack propagation diagram when N is 8 382 times and a is 3 cm

图16 N=17 835次，a=6 cm时的裂缝扩展图Fig.16 Crack propagation diagram when N is 17 835 times and a is 6 cm

图17 N=25 725次，a=9 cm时的裂缝扩展图Fig.17 Crack propagation diagram when N is 25 725 times and a is 9 cm

图18 N=33 147次，a=12 cm时的裂缝扩展图Fig.18 Crack propagation diagram when N is 33 147 times and a is 12 cm

耦合作用下，Ⅰ-Ⅱ复合型Top-Down裂缝扩展路径如图19 所示。由图19 可知：在温缩-荷载耦合作用下，Top-Down 裂缝扩展路径朝轮载方向倾斜向下，Top-Down 裂缝从1 cm 深度扩展到12 cm 深时，其宽度扩展了8.75 mm。

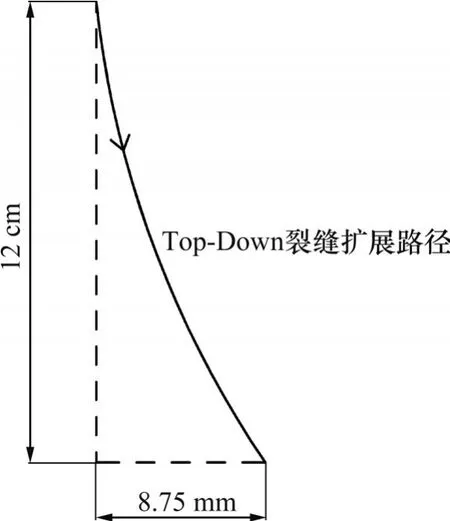
图19 耦合作用下Ⅰ-Ⅱ复合型Top-Down裂缝扩展路径Fig.19 Path diagram of Ⅰ-Ⅱ compound Top-Down crack growth path under coupling action

由于交通荷载在经过Top-Down裂缝时，会同时经过Top-Down裂缝两边，所以，实际情况往往是Top-Down裂缝在轮迹处会出现分叉的情况。不考虑裂缝分叉对各自的裂缝尖端受力的影响，实际路面车辆轮迹处基层温缩和交通荷载耦合作用下Top-Down裂缝扩展路径如图20所示。

由图20可见：在靠近车辆轮迹作用的范围内，由于交通荷载的作用，Top-Down 裂缝扩展转变为Ⅰ-Ⅱ复合型扩展。在实际路面中，车辆会同时经过Top-Down 裂缝中心的两边，因此，在车辆荷载作用范围内，Top-Down 裂缝在扩展过程中会发生分叉现象，Top-Down 裂缝之间的分叉间距可通过耦合作用建模分析获取。

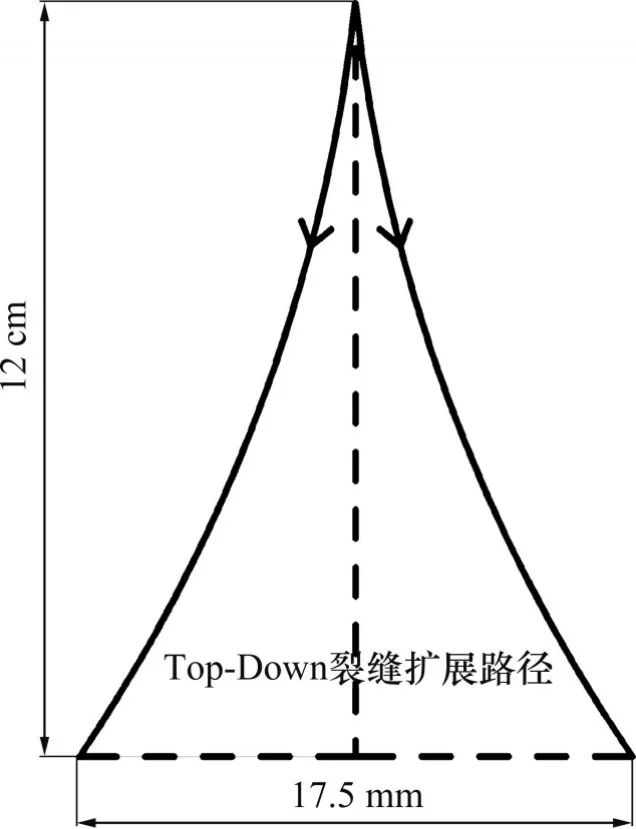
图20 耦合作用下Ⅰ-Ⅱ复合型Top-Down裂缝分叉扩展路径图Fig.20 Path diagram of bifurcation propagation path of Ⅰ-Ⅱ compound Top-Down crack under coupling action

对湖南省长潭高速公路的连配筋混凝土复合式沥青路面实体工程进行了跟踪观测和钻芯取样，如图21所示。

从图21 可见刚柔复合式路面沥青层的裂缝主要为Top-Down裂缝；实测的Top-Down裂缝扩展路径也并非是垂直向下的，而是有一定的倾斜，与扩展有限元模拟的裂缝扩展路径大致相同，这也验证了数值模拟结果的可靠性。

图21 长潭高速公路Top-Down裂缝芯样图Fig.21 Top-Down crack core sample diagrams of Changsha-xiangtan Expressway

为了与半刚性基层沥青路面进行对比，对半刚性基层(CTB)沥青路面施加图2 所示温缩应力，荷载为标准轴载BZZ-100，其他条件不变，CTB的弹性模量为2 200 MPa，泊松比为0.25。图22所示为Top-Down裂缝扩展路径图。

从图22 可以看出：当半刚性沥青路面Top-Down裂缝扩展至沥青面层底部时，需要荷载循环26 406 次，是刚柔复合式路面沥青面层Top-Down裂缝疲劳寿命的79.7%，其扩展路径几乎是竖直向下。可见与刚柔复合式路面相比，半刚性沥青路面表面一旦开裂，更容易向下扩展形成Top-Down裂缝。

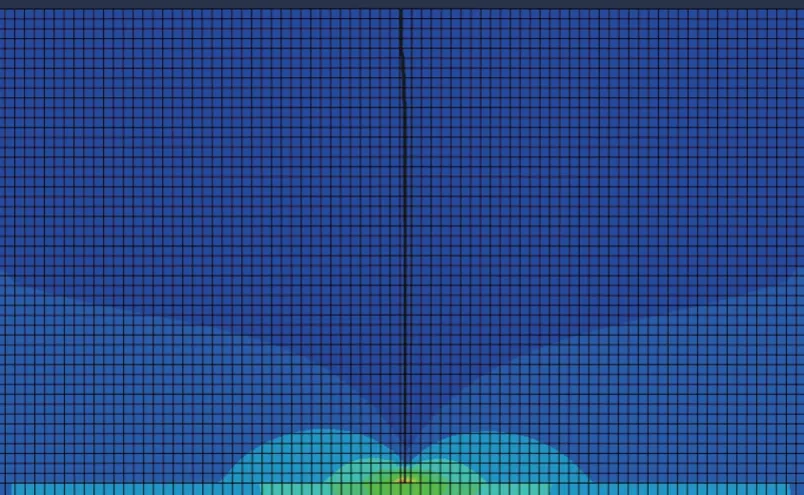
图22 N=26 406次，a=12 cm时半刚性沥青路面Top-Down裂缝扩展图Fig.22 Top-down crack propagation diagram of semirigid asphalt pavement when N is 26 406 times and a is 12 cm

通过前面的建模分析，可获取沥青面层温缩应力和交通荷载耦合作用下Top-Down裂缝扩展深度随耦合循环作用次数的关系，将其与单独沥青面层温缩应力作用下Top-Down裂缝扩展情况进行对比，对比结果如图23所示。

图23 单独温缩应力与耦合作用下裂缝扩展深度随循环荷载作用次数对比Fig.23 Comparison of crack propagation length with number of cyclic loads under separate temperature shrinkage stress and coupling action

由图23可见：在沥青面层材料在温缩-荷载耦合作用下，Top-Down 裂缝疲劳扩展寿命较单独基层温缩应力作用呈现减小的趋势，但减小幅度很小；在沥青面层材料在温缩-荷载耦合作用下，Top-Down 裂缝从1 cm 扩展到12 cm 时疲劳总寿命为33 147 次，较单独温缩作用34 142 次疲劳寿命减小了2.9%。可见交通荷载主要起到将Top-Down裂缝疲劳扩展形态由张开型转为复合型的作用，而对Top-Down裂缝的疲劳寿命影响有限。