考虑供给取消的共享停车平台泊位分配方法

张倩敏，吴先宇，宁尚彬

（北京交通大学 交通运输学院,北京 100044）

近年来，随着我国经济社会高速发展，汽车保有量快速增长，截至2021年底，全国机动车保有量已达3.93亿辆，机动车数量增长与停车位短缺的矛盾日益突出.至2018年底，我国大城市中小汽车与停车位的平均比例约为1∶0.8，据估算，全国停车位缺口已达到8 000万个［1］.

面对巨大的城市停车压力，建设大量停车设施、增设停车泊位成为停车规划的重点，但此策略仅可缓解用地宽松地区的停车困境，在用地紧张地区，增加停车泊位供给数量成本高、难度大.因此，提高现有停车设施的利用率成为解决停车难问题的主要研究方向.为提升既有停车资源的利用效率，国内外逐渐把停车共享作为一项重点策略［2］.

共享停车即利用停车泊位供需双方的错峰使用特性，将某些时段停车场闲置的空余泊位共享对外出租，并通过移动终端APP、网络平台为驾驶员匹配合理的停车泊位［3］.共享停车理论的应用与研究，最早起源于文献［4］.近年来，国内外针对共享停车系统中车位分配方法与运营机制进行了深入研究.针对大城市工作时间私人停车位的重新分配问题，Xu等［5］提出了PC-TTCC分配机制，实验结果表明所提机制可以在很大程度上节省成本.Roca-riu等［6］将寻找可行分配的问题转化为带时间窗约束的车辆路径问题.Shao等［7］研究了居民和公共用户共享使用住宅停车位及预约分配的问题，在给定需求和供给下，以平台利润最大化为目标，提出了二进制整数线性规划模型来解决车位资源的分配问题.Xiao等［8］提出用拍卖机制的方法来处理共享停车问题并约束参与者选择退出共享的可能性，在经典的DVCG机制的基础上，考虑停车时长并引入优先级属性和评价函数，提出了FRD-VCG机制.陈峻等［9］构建了不同停车需求的时空特性下的供需匹配优化模型.王斌［10］以城市中心区组合用地为研究对象，从供给-需求-分配的角度出发，研究了停车泊位共享匹配的问题.姚恩建等［11］等针对共享车位资源在实际运营中利用率不高的问题，将共享泊位利用率作为目标函数，构建了共享车位优化分配模型.为解决居住区共享泊位分配问题，蒋塬锐［12］将用户可接受的最大步行距离和停车费率视为用户偏好，研究了考虑用户偏好的居住区共享停车泊位分配模式.王盛莉［13］研究了停车用户的停车选择问题，将基于共享平台的停车选择过程分为备选停车场的初步筛选和停车泊位的选择2个阶段.路扬等［14］等从供需关系角度出发，针对“供不应求”和“供给充足”两种情况，分别建立了模型.大多相关研究是以车位供给量恒定为前提，通过决策停车请求实现车位的合理分配.孙会君等［15］研究了如何租用车位的问题，将车位租用（供给）和请求分配（需求）统一决策，提高车位利用效率，实现运营商的利润最大化.现有研究均在严格准时假设下完成的，然而在共享停车实际应用中，泊位供给方会因种种原因出现“供给取消”的行为，即在上一周期分配完成后，泊位供给方在其提交的共享时间窗内收回泊位，使得该泊位之后的共享时间窗全部不可用，导致泊位实际共享时间与提交的不一致.如果实际共享时间与提交的不一致，在严格准时假设下确定的分配对于实际的环境不再是最佳的.

为处理泊位供给方不能按约定时间提供泊位共享的违约事件，目前大部分学者均从需求方角度进行研究.例如，Jiang等［16］考虑停车用户没有按预定时间到达/离开停车位的情况，引入不准点概率对传统分配方法进行了改进.张水潮等［17］针对用户提出延时请求事件，提出了应对策略，以平台收益最大和用户步行距离最短为目标建立了优化模型并设计了缩小解集的蒙特卡洛算法对模型进行求解.傅丹华［18］针对“取消预约”突发事件，设计了供需匹配优化模型，得到了在不同取消预约概率下，车位的租用与分配方案.

在现有研究基础上，本文探讨了如何在考虑供给取消的情况下优化停车位的分配，并分析供给取消对分配的影响，讨论了供给取消对平台、停车用户及泊位供给方造成的影响；从管理角度出发提出了再分配策略并详细描述了再分配过程；通过引入再分配，建立了考虑供给取消的共享停车平台泊位分配模型；最后，通过改变模型参数，理论分析了影响最优分配的参数.

1 问题分析

共享停车系统的参与方有共享停车平台、泊位供给方和停车用户.平台运营商通过共享停车平台租用车位与提供停车服务获得利润，泊位供给方通过平台提交共享泊位信息（共享开始时刻、共享结束时刻、泊位所在停车场）并出租泊位获取收益，停车用户通过平台提交停车请求信息（停车开始时刻、停车结束时刻、可接受的最大停车费率、可接受的最大停车距离）预约停车以满足自身停车需求.平台收集共享泊位信息、停车请求信息并按照一定规则进行供需匹配的过程称为分配.平台采用周期分配的方法，每隔一定周期时间进行一次分配，即在第k个周期分配时刻tk，收集[tk-1，tk]内的停车请求信息和泊位共享信息，判断有哪些停车用户和共享泊位参与分配，从系统效益角度出发确定最优分配方案.

若供给方要取消供给，需提前向平台提出申请.根据上一周期分配结果的不同，供给方提交供给取消请求时，泊位状态会出现泊位未分配、泊位已分配未占用和泊位已分配已占用3种情况，供给取消时泊位与需求关系如图1所示.以泊位A为例，泊位未分配如图1（a）所示，即在上一周期分配时，该泊位未分配给任何停车用户；泊位已分配未占用如图1（b）所示，即在上一周期分配时，该泊位已分配给用户1和用户2，在供给取消开始时刻，用户1已完成停车，用户2尚未开始停车，供给取消后，若平台不采取任何措施，用户2将无车位可停；泊位已分配已占用如图1（c）所示，即在上一周期分配时，该泊位已分配给用户1、用户2和用户3，在供给取消开始时刻，用户2尚未完成停车，此时，供给取消将影响用户2和用户3停车.

图1 供给取消时泊位与需求关系图Fig.1 Schematic diagram of the relationship between parking spaces and demands under supply cancellation

考虑供给取消情况及停车泊位的基本理论，给出本泊位分配模型的6个假设条件.

1）假设不同停车场的停车位具有异质性，同一停车场的停车位具有同质性.

2）假设平台租用某车位，则租用其整个空闲时段.

3）假设停车用户严格遵守提交的需求时间窗.

4）假设停车用户的步行距离为停车场出口与目的地的距离.

5）假设用户被分配失败次数大于最大分配失败次数，则选择退出系统；否则，选择留在系统等待下一次分配.

6）假设供给一旦取消，其之后的共享时间窗则全部不可用.

2 考虑供给取消的共享泊位分配

2.1 供给取消情况下共享泊位再分配策略

供给取消不仅会导致原本被分配了泊位的停车用户无车位可停，而且会影响平台收益.因此，我们提出了再分配策略，对因供给取消而导致无车位可停的停车用户进行重新分配，一方面最大限度上减少无车位可停的停车用户数量，另一方面平台可通过再分配获得一定的收入，可弥补因供给取消而导致的平台损失.泊位再分配过程流程图如图2所示.

图2 再分配流程图Fig.2 Reallocation flowchart

平台接收到供给取消请求时，首先判断泊位的状态，若泊位未分配，则不需要考虑再分配问题.若泊位已分配，统计被分配至泊位的停车用户，判断用户的停车开始时刻ts与供给取消开始时刻tcancel的关系，停车开始时刻位于泊位取消开始时刻之后（ts＞tcancel）的用户参与再分配.

再分配方法分为即时性再分配和延时性再分配.即时性再分配即平台在接收到供给取消请求后根据再分配停车用户的停车开始时刻ts与第k+1个周期分配时刻tk+1的关系，对ts＜tk+1的停车用户，平台立即进行再分配.即时性再分配发生在平台第k个周期分配和第k+1个周期分配之间的任意时刻，分配方法参考文献［12］.延时性再分配即平台在接收到供给取消请求后，若再分配停车用户不满足即时性分配条件，则将其放入分配池中，待第k+1个周期分配时刻与其他用户一同分配.在供给充足条件下，所有用户需求均能得到满足.在供不应求情况下，优先满足再分配用户的停车需求，通过分配优先系数的设置，实现再分配用户的优先分配［14］，令再分配用户的优先级系数q=1.5，其他用户q=1.

参与再分配的停车用户在供给取消提交时刻存在两种状态：已到停车场（ts=tcancel）和未到停车场（ts＞tcancel）.对于已到停车场的停车用户，优先把停车用户分配至当前停车场，若当前停车场没有满足用户停车需求的泊位，则将停车用户分配至其他停车场，并对停车用户进行补偿.对于未到停车场的停车用户，被分配至各停车场的概率是相等的，令补偿因子为φ=0.

2.2 基于再分配策略的共享停车分配模型

基于周期分配方法，在已知供给取消信息前提下，结合再分配策略，从平台运营商和停车用户角度提出了考虑供给取消和再分配的共享泊位分配模型.

2.2.1 变量参数定义

研究区域内共有N个提供共享泊位的停车场，将共享停车平台运营时间划分为p个时段.平台每隔周期时间T进行一次分配，假设在预设的时刻，参与分配的停车用户集合I包括上一次分配时分配失败的用户请求和本周期内新接收的用户请求.用户i请求信息包括停车时间窗(tis，tie)、可接受的最大步行距离dio、可接受的最大停车费率αio和目的地D，其中，tis和tie分别是用户i的停车开始时刻和结束时刻所在时段.考虑到泊位会存在多个连续共享时间窗的情况，将泊位分配转化为时间窗分配，令每个独立的连续共享时间窗代表一个虚拟泊位供给方，参与分配的泊位供给方集合J包括占用结束后释放出来的车位、本周期内新接收的车位.相较于传统的泊位数量利用率，所提出模型更侧重提高时间资源的利用率.泊位j共享信息包括泊位共享时间窗(tjs，tje)、泊位所在停车场n，停车场n的单位时间租用成本为βn，单位时间停车费用为αn，距停车用户i的 目的地距离为din，其中，tjs和tje分 别 是 泊 位j的 共享开始时刻和结束时刻所在时段.

用户u和用户v（u，v∈I且u≠v）的停车时间窗关系cuv为

式中：tus表示用户u预约停车开始时刻，tue表示用户u预约停车结束时刻；tvs表示用户v预约停车开始时刻，tve表示用户v预约停车结束时刻.当用户u和用户v的停车时间窗存在冲突时，cuv=1；否则，cuv=0.

用 户i与 泊 位j（i∈I，j∈J）的 时 间 窗 从 属 关系bij为

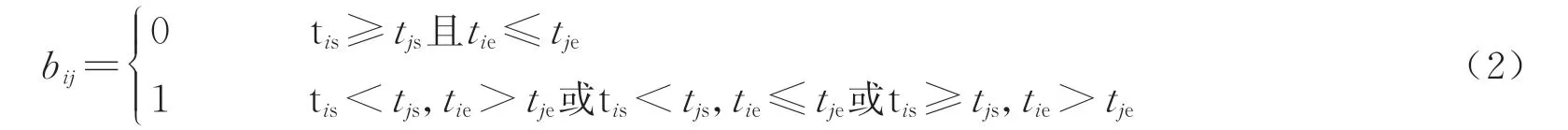
式中：tis表示用户i预约停车开始时刻，tie表示用户i预约停车结束时刻；tjs表示泊位j共享停车开始时刻，tje表示泊位j共享停车结束时刻.当泊位j的共享时间窗满足停车用户i请求时间窗，bij=0；否则为1.

yjn表示泊位j与停车场n的关系，泊位j属于停车场n时，yjn=1；否则为0.

取消供给的泊位供给方集合用Jcancel表示，参与再分配的用户集合用Ia表示.再分配时，用户i（i∈Ia）是否到达泊位j（j∈Jcancel）所在停车场的状态ai为

式中：若用户i已到达泊位j所在停车场，则ai=1，否则ai=0.

模型决策变量即各用户的泊位分配方案xij为

2.2.2优化目标

第k个周期分配时，平台收集第k个周期内的需求信息、供给信息和供给取消信息，判断参与分配的停车用户和共享泊位，从系统效益最大出发确定最优分配方案.为体现分配的合理性与科学性，建立了线性整数规划模型，在考虑供给取消的情况下，确定一个最优的分配方案.针对共享泊位和停车用户的供需关系，建立了泊位供给紧张和泊位供给充足两种情况下的目标函数：

1）当共享停车系统中的泊位状态处于“供给紧张”状态下，为使泊位资源得到充分利用，以共享时长利用率最大为目标建立了目标函数并兼顾再分配用户的优先级，由此可得目标函数ω1为

2）当共享停车系统中的泊位供应非常充足时，目标函数为平台收益最大化，平台收益由每个分配周期内出租车位所获得的收入减去租用车位的成本和损失组成，由此可得目标函数ω2为

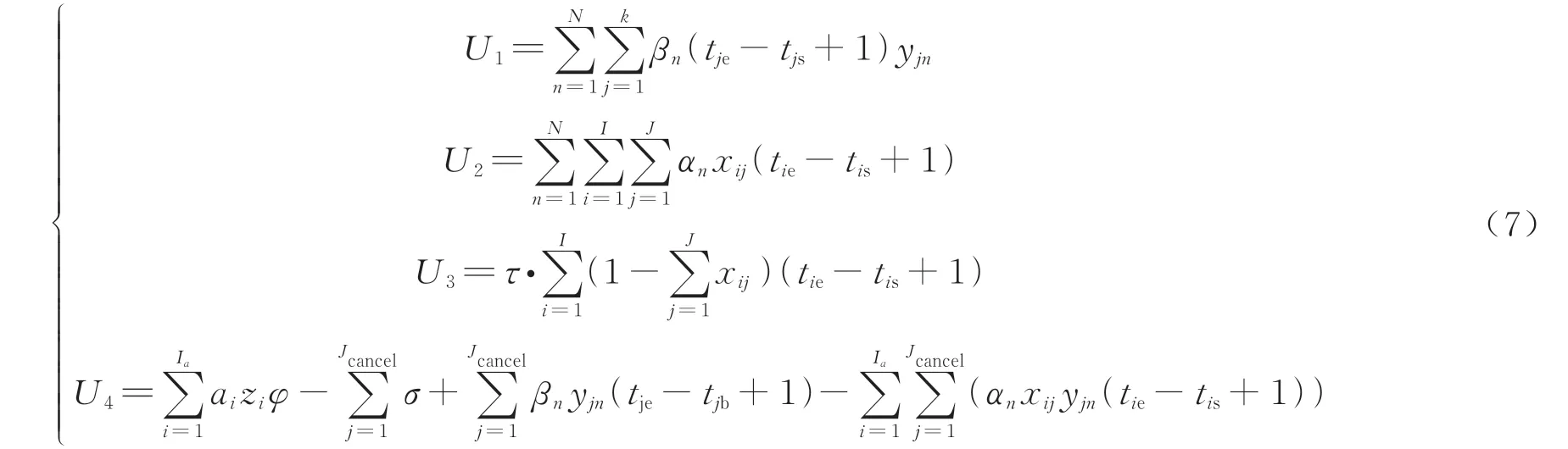
式中：U1表示租用车位的成本；Jk为第k个周期内新接收的泊位集合；U2表示出租车位的收入；U3则表示因拒绝请求产生的损失；τ表示请求惩罚系数；b为惩罚因子，当供小于求时，平台将拒绝部分用户请求，并提示用户分配失败，因产生分配失败的情况会使用户对平台的长期使用造成影响，所以引入请求惩罚系数对平台收益进行折减；U4表示因供给取消产生的损失；zi表示再分配停车用户i两次被分配的泊位是否在同一个停车场，是则为0，否则为1；σ为惩罚因子；tjb为供给取消时刻.

2.2.3 约束条件

1）需求空间约束.

一个停车需求至多被分配到一个泊位上，其具体形式为

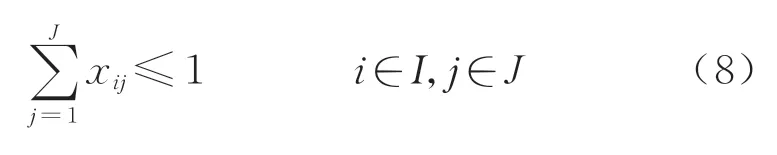
2）需求时间约束.

时间冲突的两个停车需求不能被分配到同一个泊位上，其具体形式为

式中：xuj表示泊位j分配给用户u；xvj表示泊位j分配给用户v.

3）供需时间窗约束.

停车需求的时间窗满足泊位时间窗时才可被分配到该泊位上，其具体形式为

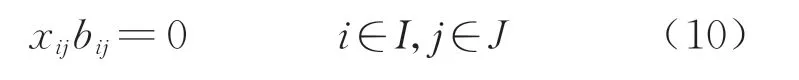
4）步行距离约束.

用户停车后步行距离不能超过其所能接受的最大步行距离，其具体形式为

5）停车费率约束.

停车费率不能超过用户所能接受的最大停车费率，其具体形式为

2.3 模型求解算法

由于再分配模型考虑了泊位供给方的随机性特征，传统的优化算法难以解决这类复杂问题，而遗传算法对于随机性问题具备较好的适应性.在求解较为复杂的组合优化问题时，相对一些常规的优化算法，通常能够较快地获得较好的优化结果.因此，选择采用遗传算法进行求解.

用遗传算法进行求解时，首先通过随机匹配的方式获得若干初始可行分配方案（即初始种群），并对分配方案中泊位编号和用户编号进行编码，将其转换为二进制，随后根据模型目标函数计算种群中各个体的适应度，适应度的大小代表了个体基因遗传给下一代的概率，通过选择、交叉、变异等操作反复更新种群，迭代完成获得算法最优解.算法采用Visual Studio 2019进行编程.算法求解流程如图3所示.图3中，Gen表示迭代次数.

3 案例仿真

3.1 评价指标

采用收益、泊位利用率和用户满意度作为评价指标对模型进行评价.

收益是共享停车平台运营商的利润，平台作为第三方盈利机构，目标是利润最大化，供给取消无疑会影响平台利润.收益ρ可表示为

泊位利用率是衡量共享泊位是否得到充分利用的重要指标.因为共享泊位资源不能简单地用泊位数来描述，还需考虑可供使用的时长.因此，采用泊位共享利用时长与总可利用时长的比值来表示泊位利用率θ，其具体形式为

用户满意度体现在有无车位可停、被分配泊位的停车费率和停车场距用户目的地的步行距离，模型约束条件中已考虑了停车费率和步行距离，因此采用有车位可停的用户比例来表示用户满意度γ，其具体形式为

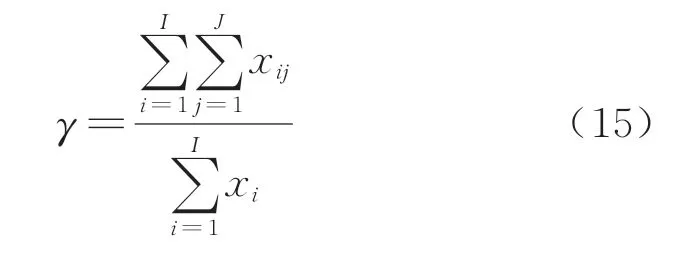
式中：xi表示第i个停车用户的相关参数都等于1，i∈I.

3.2 案例分析

选取北京新荟城购物中心及其周边的4个停车场作为实验目标，北京新荟城购物中心地下停车场现有B1、B2两层，共有车位300个，新荟城购物中心属于望京商圈，周边有北京凯德MALL望京、北京新世界百货（望京店）、北京方恒购物中心、北京合生麒麟新天地等各大商场，商业区密集，地理位置优越，周边路网发达，交通便利，客流量大，泊位占有率较高且周末泊位占用率普遍高于工作日，这主要是由于周末娱乐、购物等出行需求增加.另外，一天当中，泊位占用呈现明显的高峰和平峰.这主要与居民出行特征有关，白天，由于商场工作人员上班和顾客的到达和离开，泊位需求量较大，停车占用处于高峰；夜间，停车位大多处于闲置状态，可用于夜间长时共享停车.在停车时长方面，新荟城主要的停车群体是商场工作人员和弹性购物消费人员，商场工作人员由于上班时间的限制，一般是长时停车.弹性购物消费人员考虑到停车费用，一般在出行目的达成后就选择离开商场，为短时停车.

以目的地为新荟城购物中心的停车用户作为需求来源，邻近3个居民区附属停车场和一个商务办公区附属停车场作为泊位供给方为过量停车需求提供泊位，4个停车场的位置关系如图4所示，共有500个车位.

图4 停车场位置Fig.4 Location of parking lots

假设共享平台开放时间为0∶00-24∶00，将其划分为96个时段，即每个时段15 min，平台分配周期T=1 h.运营管理者租用共享车位的成本为1.5元/时段，停车用户的停车费率为2.5元/时段.令停车用户可接受的最大分配失败次数为2，惩罚因子σ=15，补偿因子为φ=10，遗传算法的交叉概率取0.7，变异概率为0.1，种群数量取为300.假设供给取消服从泊松分布，以2018年4月8日8∶00至2018年4月9日8∶00的1204条停车数据为例进行仿真.

1）数据预处理.

假设用户均在停车前两小时提交停车请求，将用户提交请求时间，停车开始时间和停车结束时间按照时段来划分.随机生成用户可接受的最大停车费率和最大步行距离，依据经验和实际停车场收费情况，最大停车费率的取值范围αio是3～6元/h，最大步行距离doi的取值范围是300～500 m.计算2018年4月8日8∶00至2018年4月9日8∶00时段内目标停车场各车辆停车时长.各数据预处理结果如表1所示.

表1 数据预处理结果Tab.1 Data preprocessing results

按照小时将一天分配成24个周期，平台分配周期T=1 h，统计得到各分配周期的停车特性如图5所示.

由图5可知，停车需求分布呈现出明显的3个高峰时期，这是因为商场工作人员上班需要，泊位需求逐渐增加，至中午由于商场就餐人数的增加，泊位需求达到高峰，由此出现了第1个和第2个需求高峰.饭点过后，需求开始下降，至晚上，由于晚间购物消费等原因，需求又呈现一高峰，即第3个高峰.夜间停车需求最少，泊位处于闲置状态.

图5 停车分布特性Fig.5 Characteristics of parking cycle distributions

2）模型有效性验证.

为了证明考虑再分配策略的模型有效性，假设泊位供给充足，分别对考虑再分配和不考虑再分配的模型仿真结果进行对比，模型对比结果如表2所示.

由表2可知，考虑供给取消随机性和再分配时，平台各分配周期的收益、泊位利用率和用户满意度均优于在供给取消情况下未考虑再分配的模型，平台收益、泊位利用率和用户满意度分别提高23.73%、18.45%、30.61%.

表2 模型对比结果Tab.2 Comparison results for different models

假定停车用户数量固定，泊位数量从100逐渐增加到600，计算各分配周期内的收益、满足的再分配用户需求数量和满足的预约用户需求数量如图6所示.

由图6可知，收益随着泊位数量的增加呈先增后减的趋势，需求得到满足的停车用户数量持续增加，当共享泊位数量S=500时，平台收益最大且满足的停车用户数趋于平缓.另外，满足的再分配用户数量先增后减，这是因为泊位供给紧张时，优先满足再分配用户的需求，当泊位数量持续增加至充足时，平台为使得收益最大可能会选择满足预约用户的需求而使得满足的再分配用户数量有所减少.这与模型目标函数也是相符的，从侧面反映了考虑再分配策略的模型有效性.

图6 需求得到满足的用户数量随泊位数量的变化Fig.6 User number variation with parking space after the needs are satisfied

3）平台仿真结果分析.

通过对不同时间的停车需求数和泊位利用率进行统计得到变化曲线如图7所示.

由图7可知，在供给紧张（S=200）的状态下，在11∶00-15∶00时间段，泊位几乎全部都被占用，且此时段内的停车需求仍处于高态势并且14∶00之后有持续增长的趋势，平台接收到供给取消请求时，可根据当前泊位占用情况判断是否接受供给取消请求.在供给充足（S=500）状态下，泊位利用率一直处于较低的状态.

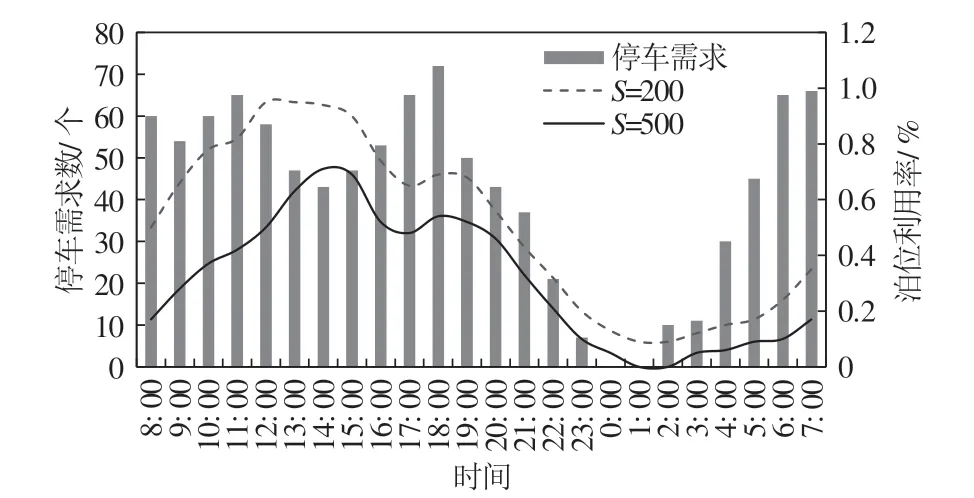
图7 停车需求数和泊位利用率随时间的变化Fig.7 Variation of parking demand and utilization rate of parking spaces over time

在泊位供给固定的情况下，平台收益随接受的预约需求数的趋势如图8所示.

图8 停车需求对收益的影响分析Fig.8 Analysis of the impact of parking demand on revenues

由图8可知，在停车用户数小于700时，S=200时的平台收益始终大于S=500时的平台收益，这是因为停车用户较少时，较少的泊位就可满足停车需求，而较多的泊位供给往往因支付较多的租用成本而导致收益减少.另外，从S=500的曲线可以看出，收益达到最大时，停车用户请求接受率为89%左右，这说明停车用户并不是接受的越多越好.

为了进一步研究供给取消条件下车位供给与需求的关系，假设泊位供给固定，令停车用户需求数逐渐增加，并计算供需比（停车泊位数与停车用户的比例），得到供需比与收益和泊位利用率曲线如图9所示.

由图9可知，随着供需比的增加，平台收益呈先增后减的变化趋势，泊位利用率先是比较平缓而后逐渐减少.当供需比为0.25时，平台收益最大并且泊位利用率处于较大值，由此得出在考虑供给取消的前提下，平台最佳的泊位供给与停车用户比例为0.25.当停车用户总数已知，供给取消分布情况已知或可预测的条件下，通过该比例可以确定最佳的泊位供给数［18］，为共享停车平台的运营管理提供参考.

图9 供需比与收益和泊位利用率的关系Fig.9 Relationship between the supply-demand ratio,revenue,and space utilization

3.3 灵敏度分析

灵敏度分析实验目的是分析在不同供给取消数量和不同共享泊位数量下的情况下，评价指标（即收益、泊位利用率和用户满意度）的变化情况.除了测试的参数，其他值与基本实验中假设的相同.

1）供给取消数量η.

设η从20到80变化，步长（表示不同情况自变量的单位变化量）为20，得到不同数量下的评价指标值如表3所示.

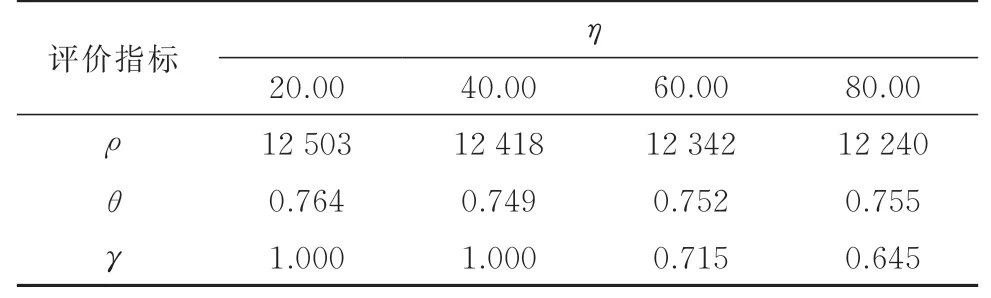
表3 不同供给取消数量下的评价指标Tab.3 Indicators under different supply cancellation quantities

由表3可知，收益和用户满意度都随着η的增加而降低.这一结果表明供给取消是负面因素.尽管由于再分配和惩罚措施，平台可能会获得一定收入，但收入远低于它带来的损失.随着η的增加，泊位供应越来越少，可满足的停车需求时长也越来越少，平台不得不拒绝部分用户的停车请求，导致这部分用户无泊位可停，从而平台收益和用户满意度均减少.η从20增加到80时，收益由12 503元下降至12 240元，满意度从1下降到0.6左右.在不同的供给取消数量下，泊位利用率变化不大，这是因为泊位利用率等于泊位共享利用时长与总可利用时长的比值，供给取消的同时，可满足停车需求的实际共享时间也减少.基于分析结果，建议平台需要应用一些管理方法来尝试控制供给方的不守时行为.虽然供给取消的不确定性在实践中是不可避免的，但应尽量将供给取消的概率保持在较低的值.

2）共享泊位数量S.

设S取值从300到500，步长（表示不同情况自变量的单位变化量）为100，得到不同泊位数量下的评价指标如表4所示.

表4 不同泊位数量下的评价指标Tab.4 Indicators under different supply quantities

由表4可知，随着S的增加，平台收益先增加后减少.这是因为停车需求数量保持不变.起初，由于停车位不足，只有少数需求得到满足.随着泊位的增加，被满足的需求数量逐渐增加，这导致平台收益增加.然而，泊位逐渐增加至供过于求时，几乎所有的停车需求都得到满足，供应过剩导致大量泊位闲置，导致收入较少，因此当S值较大时，平台收益随之减少.利用率的变化也反映了类似的原理.用户满意率随着泊位数量的增加而增加，当S达到500时，平台可以满足所有需求.

4 结论

1）从供给角度出发，针对“供给取消”这一影响平台收益和停车用户停车可能性的失约事件，提出了考虑供给取消的共享泊位分配方法.通过分析供给取消事件对平台和停车用户的影响，提出再分配策略.基于现有泊位分配模型，构建了在再分配策略下，以平台收益为优化目标并综合考虑用户从停车场至目的地步行距离和用户可接受的最大停车费率的泊位分配模型，从平台自身利益及保证用户偏好两个角度出发，确定最优分配方案.

2）以新荟城购物中心地下停车场及其邻近的停车场为案例进行仿真实验，与常规方案相比，考虑再分配的共享停车平台泊位分配方案下的平台收益、泊位利用率、用户满意度分别可提高23.73%、18.45%、30.61%，所提方法可有效提高平台收益并在一定程度上保障停车用户和泊位供给方的效益.并且从供需问题着手可以在根本上提高平台的运营收益，为共享停车平台的运营管理策略提供理论参考.