基于自适应反演法的轮式AGV轨迹跟踪方法

曹小华 张 朝 周志刚 王俊武

(武汉理工大学交通与物流工程学院1) 武汉 430063) (武汉普罗劳格科技股份有限公司2) 武汉 430030)

0 引 言

自动导向车(automated guided vehicle，AGV)是一种无人操纵的自动化搬运设备，是现代物流系统中的关键设备，被广泛应用于仓储、医疗、军工等领域[1-2].轨迹跟踪控制是AGV自主导航中的关键技术之一，是AGV执行各种任务的基础.由于AGV是典型的非完整性约束系统，其轨迹跟踪控制技术是目前研究的难点[3]，对此，国内外学者进行了大量的研究.PID控制以其简单、易于实现的优点成为目前工业现场所应用最多、最成熟的反馈控制算法，但是传统PID控制中的参数固定且难以确定[4]，在AGV运动控制中难以达到理想的效果.滑膜控制因其响应快、鲁棒性较好，近年来，在AGV轨迹跟踪控制中研究较多.但是在实际应用中，由于滑膜控制开关的频繁切换，系统极易出现抖振现象[5].Ye等[6-7]将神经网络算法分别与PID控制和滑膜控制结合，较好地解决了PID控制和滑膜控制中的缺点，但增加了算法的复杂度，降低控制的实时性.线性二次最优控制(LQR)是一种针对线性模型来设计的控制策略，可以得到最优的解析表达式，同时能兼顾多项性能指标.但是LQR本质上是针对线性系统的无约束优化方法，求解时假设控制量不受约束并且依赖于精确的数学模型，在参数时变和外部扰动存在时无法保证系统的鲁棒性[8].模型预测控制(MPC)可以处理多变量约束优化控制问题且不依赖于精确的控制模型，适用范围非常广泛，但是MPC算法的计算量巨大，同样会降低轨迹跟踪的实时性[9].Ghasemi等[10]使用的分布式MPC方法提高了计算速度，但需要更多的硬件支持，增加成本.席雷平等[11]使用反演法设计了四轮移动机器人轨迹跟踪控制算法，并利用Lyapunov方法证明了系统的全局稳定性，能够对满足一定条件的参考轨迹实现全局渐近跟踪.彭继慎等[12]建立了轮式移动机器人的运动学和动力学模型，采用反演法并结合滑膜控制设计了轨迹跟踪控制器，通过仿真验证了其有效性.相比于其它算法，反演法具有计算量小、稳定性好以及易于实现的优点.但是，基于反演法所设计的AGV轨迹跟踪控制器中存在较多的参数，目前，绝大多数学者都采用固定参数的方法，然而在不同的作业环境下，固定参数的方法难以取得理想的效果.

文中采用反演法对轮式AGV的轨迹跟踪控制器进行设计，并在研究反演法轨迹跟踪控制器中参数对控制器性能的影响的基础上提出一种参数调整策略，用以提高控制器对不同工况的适应能力.

1 反演法轨迹跟踪控制器设计

1.1 跟踪问题描述

AGV为前转后驱式AGV，两后轮为差速驱动轮，两前轮为阿克曼转向结构转向轮，AGV模型图见图1.

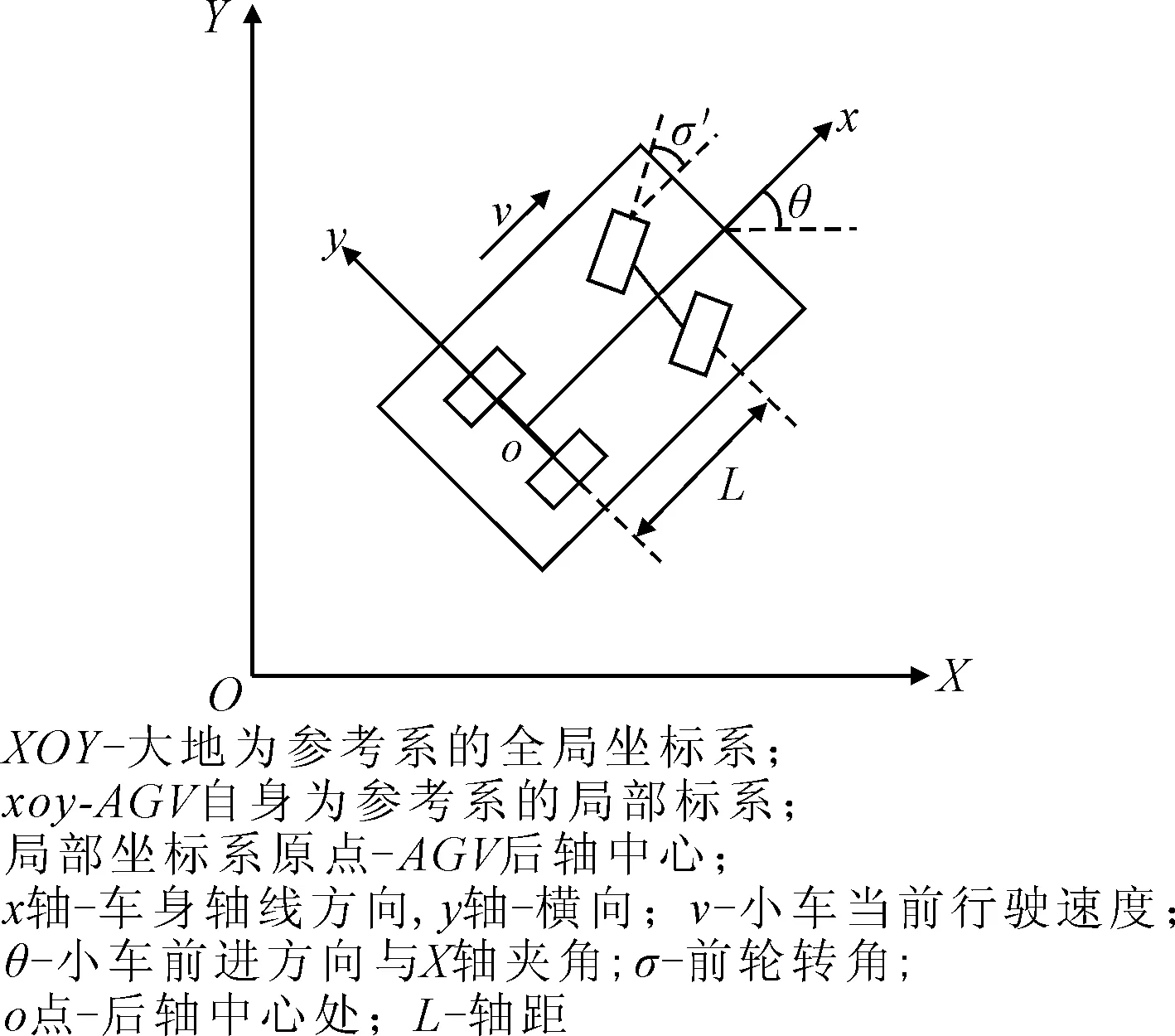
图1 AGV运动模型

设局部坐标系原点o在全局坐标系下的坐标为(x,y)，为了简化模型，假设AGV在运动过程中做无侧滑的纯滚动运动，因此AGV在行驶过程中无横向速度，由此可得AGV的运动约束：

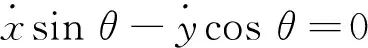
(1)

根据约束方程和几何关系可以得到AGV的运动学模型.

AGV的轨迹跟踪是非线性系统问题，需要根据AGV当前的运动状态、位姿误差和期望运行轨迹求出AGV实时的控制率，使得AGV沿着期望运动轨迹或近似沿着期望轨迹运动.AGV在进行轨迹跟踪时，每个采样时刻都对应一个期望的位姿点，由此可以计算出AGV的跟踪误差.AGV的轨迹跟踪误差示意图见图2.在全局坐标系下，AGV当前实际位姿坐标为q=[xyθ]T，当前位姿时刻所对应的参考位姿为qr=[xryrθr]T.位姿误差在全局坐标系下由e=[xeyeθe]T表示，在局部坐标系下由el=[exeyeθ]T表示.

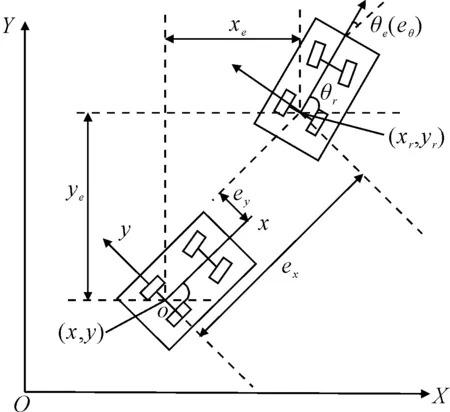
图2 AGV轨迹跟踪误差示意图

AGV的期望轨迹上的每个采样点都应满足AGV的运动学方程，为

(3)

根据图2中所展示的几何关系，局部坐标系下的位姿误差向量为

(4)

对式求导并结合非完整约束可求得AGV的位姿误差微分方程.

(5)

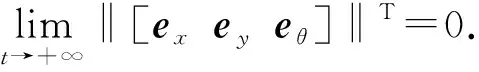
1.2 轨迹跟踪控制率设计

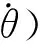
假设eθ→0，把ex作为虚拟控制量，构造部分Lyapunov函数.

(6)

当eθ→0时，对式求导可得：

(7)

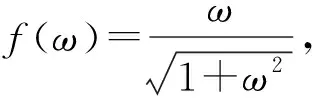
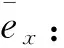
(8)

(9)

式中：t2为大于0的实数.

对V2进行求导，其结果为

(10)

根据式(10)设计系统的间接控制率为

(11)

式中：t1、t2、t3、t4均为大于0的实数

由此可以得到AGV的轨迹跟踪控制直接控制率为

(12)

式中：t1、t2、t3、t4均为大于0的实数

1.3 控制器性能分析

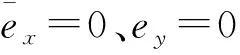
(13)

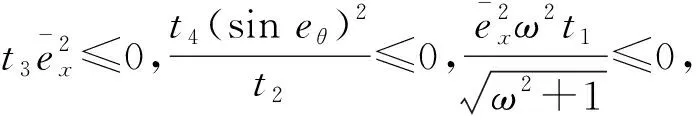
为了进一步分析该控制器的性能，使用第三章搭建的Carsim-Simulink仿真模型对该控制器进行仿真测试.为了测试该控制器在不同作业条件下的控制效果以及控制器中参数对控制器的影响，使用两组选用不同参数的控制器分别在2 m/s和5 m/s的期望速度下进行仿真测试.具体参数如下：参数组1：t1=1，t2=0.8，t3=1，t4=1.5.参数组2：t1=1，t2=0.3，t3=1，t4=6.所有仿真路径都为半径为50 m的圆.车辆在全局坐标系下的初始位姿为[-3-2-π/12]T.仿真结果见图3.

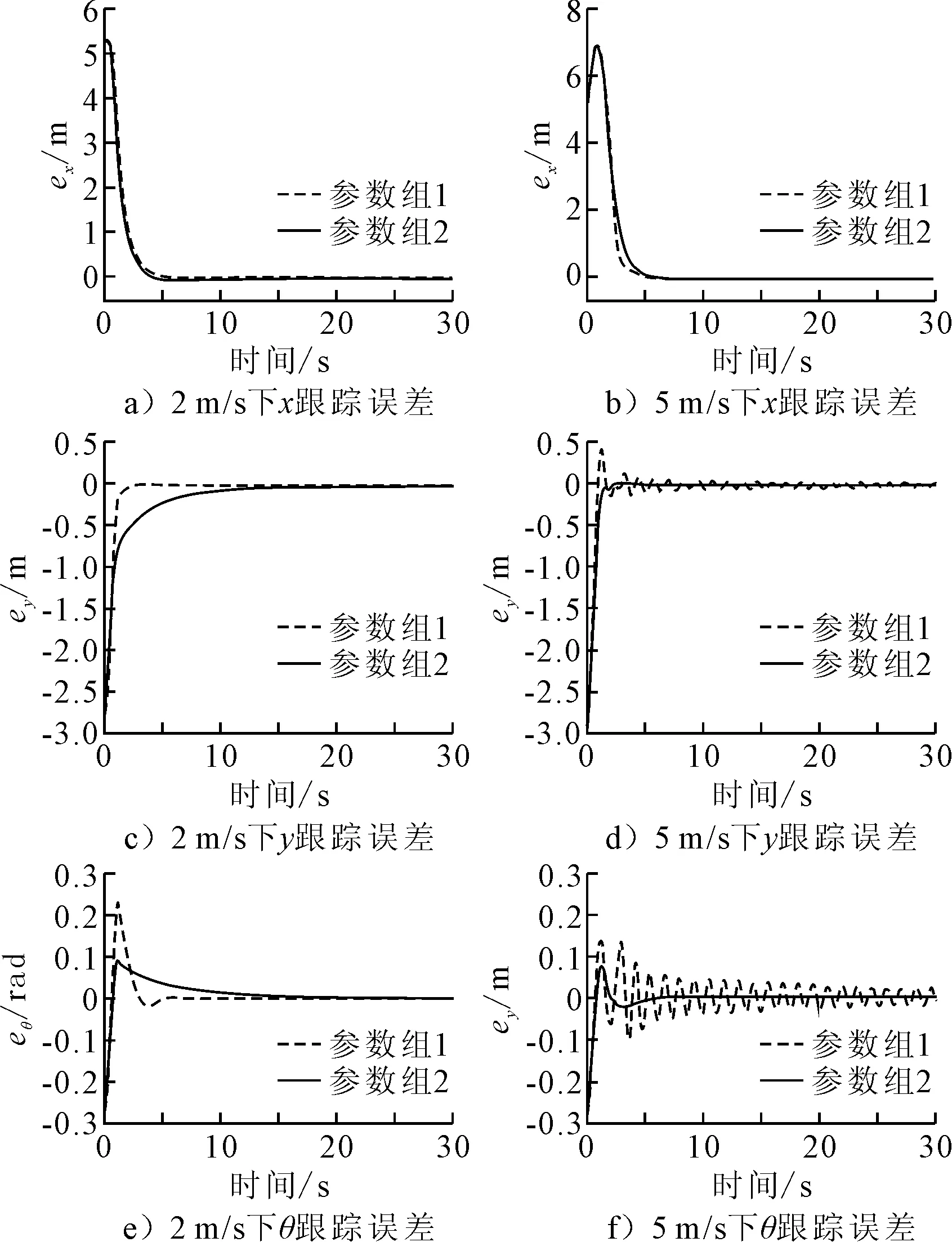
图3 仿真结果

由图3可知：控制器在使用参数组1进行控制时，在2 m/s的期望速度下可以很好的跟踪目标轨迹，但是在5 m/s的期望速度下会造成系统震荡.控制器在使用参数组2进行控制时，在5 m/s的期望速度下能很好的跟踪目标轨迹，但是在2 m/s的期望速度下收敛较慢.因此可以得出：基于反演法所设计的轨迹跟踪控制率中的参数对控制器的性能有很大的影响，在不同的作业环境下，使用固定参数难以取得理想的跟踪效果.

2 控制器参数调整策略

2.1 模糊控制变量的确定

由控制率式可知，速度控制与ey和ex两种误差有关，影响程度由t1和t3决定，理论上增大t1和t3的值可以加快ex和ey的收敛速度，但是由于车辆的加速度和系统延时的限制，增大t1和t3对加快ey和ex的收敛的效果并不明显，并且过大的t1和t3会引起速度震荡，同时当偏差ey和ex较大时增大t1和t3会使得速度控制量过大，从而使得角度控制量过小，这样反而会减慢ey和eθ的收敛速度，因此文中将参数t1和t3设置为固定值.转角的控制与ey和eθ两种误差有关，影响程度由t2和t4来决定，增大t2和t4可以提高ey和eθ的收敛速度，但是t2和t4对车速比较敏感，当车速较大时，t2过大会使得系统震荡，过小会让ey收敛过慢，同时t2与t4需要成一定比例，大的期望车速对应的t2与t4的比值更大.因此使用模糊控制器自适应调节t2和t4的值.

2.2 输入输出模糊化

文中设计了1个三输入，两输出的模糊控制器，将期望车速、横向偏差和航向偏差作为模糊控制器的输入，将参数t2和t4作为模糊控制器的输出.输入输出的论域档级对模糊控制器的性能有很大影响，过多的档级会增加算法的复杂度，降低控制的实时性，而过少的档级会降低模糊控制的精准度.根据实际运行情况，分别将速度从0～10 m/s、横向误差从0～2 m、航向误差从0°～90°、参数t2从0.1～1.5及参数t4从1～8分为七个论域.同时根据各模糊变量确定其隶属度函数，文中选择三角形隶属度函数作为所有模糊变量的隶属度函数.

2.3 模糊规则的确定

设计模糊推理规则的主要依据如下：1、当车速较大时，为了防止ey对转角影响过大而导致系统抖动，应该输出较小的t2，同时为了平衡ey和eθ对角度控制的影响，需要输出较大的t4；2、当ey较大时，为了加快ey的收敛速度，应该输出较大的t2；3、当eθ较大时，为了加快eθ的收敛速度，应该输出较大的t4；按照上述控制规律并结合大量仿真调试经验，得到t2和t4的模糊推理规则，见表1～2.

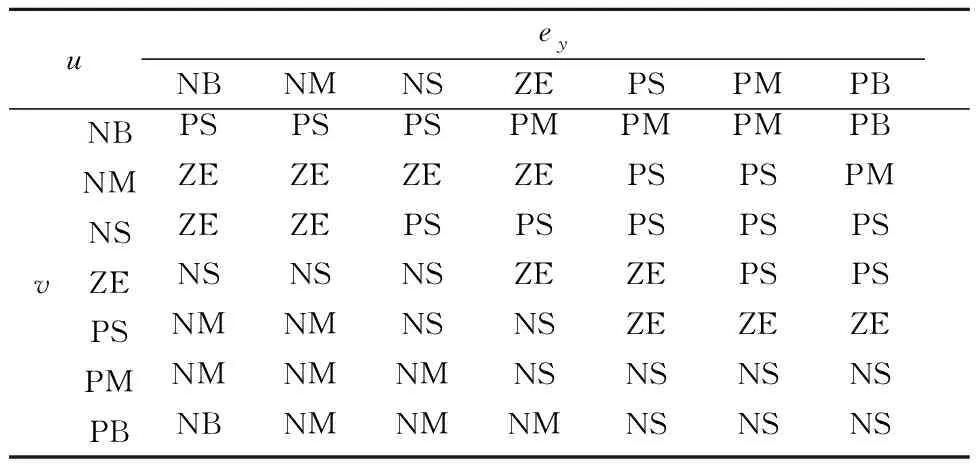
表1 参数t2的模糊控制规则

最终模糊控制器会根据输入参数和模糊规则输出合适的t2和t4的值，将得到的值代入控制率式中，可以得到AGV在不同的车速、航向偏差和横向偏差下的实时控制率，有效的提高轨迹跟踪算法的收敛速度和鲁棒性.

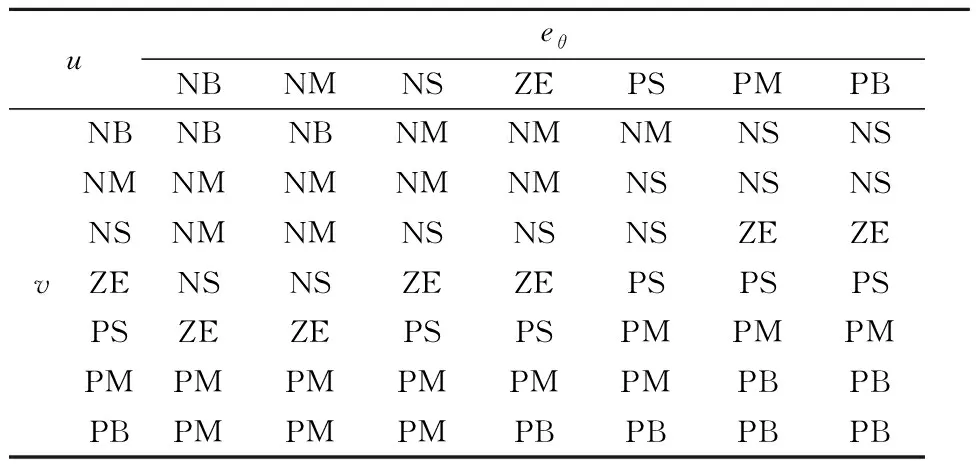
表2 参数t4的模糊控制规则

3 仿真与实验

3.1 仿真验证

搭建的联合仿真模型见图4.为验证所设计的控制器在不同作业条件下都能有很好的控制效果，分别在2，5和8 m/s的期望速度下对所设计的控制器进行仿真实验，结果见图5.仿真路径为半径为50 m的圆.车辆在全局坐标系下的初始偏差为xe=5.8 m；ye=-1.24 m；θe=-π/12.

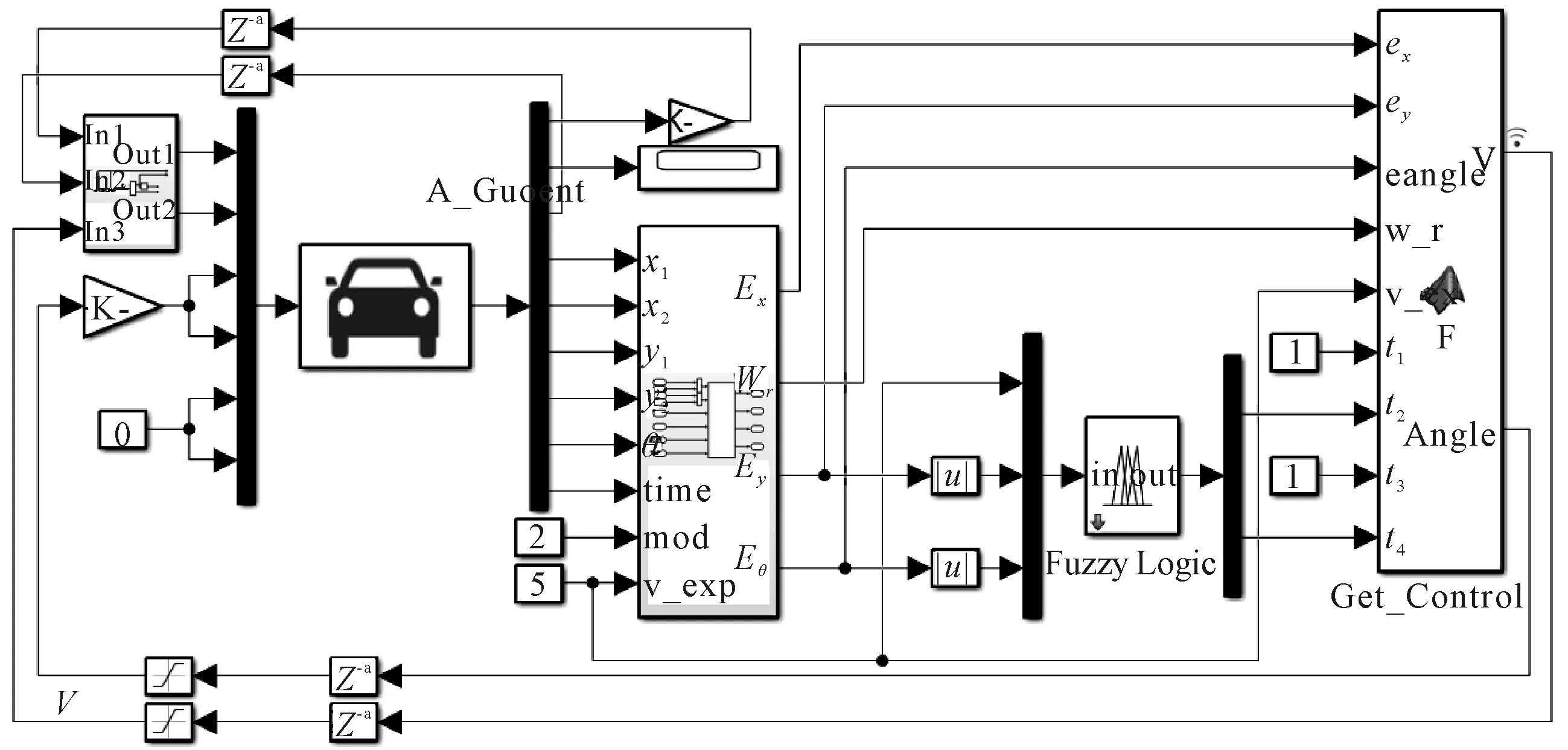
图4 联合仿真模型

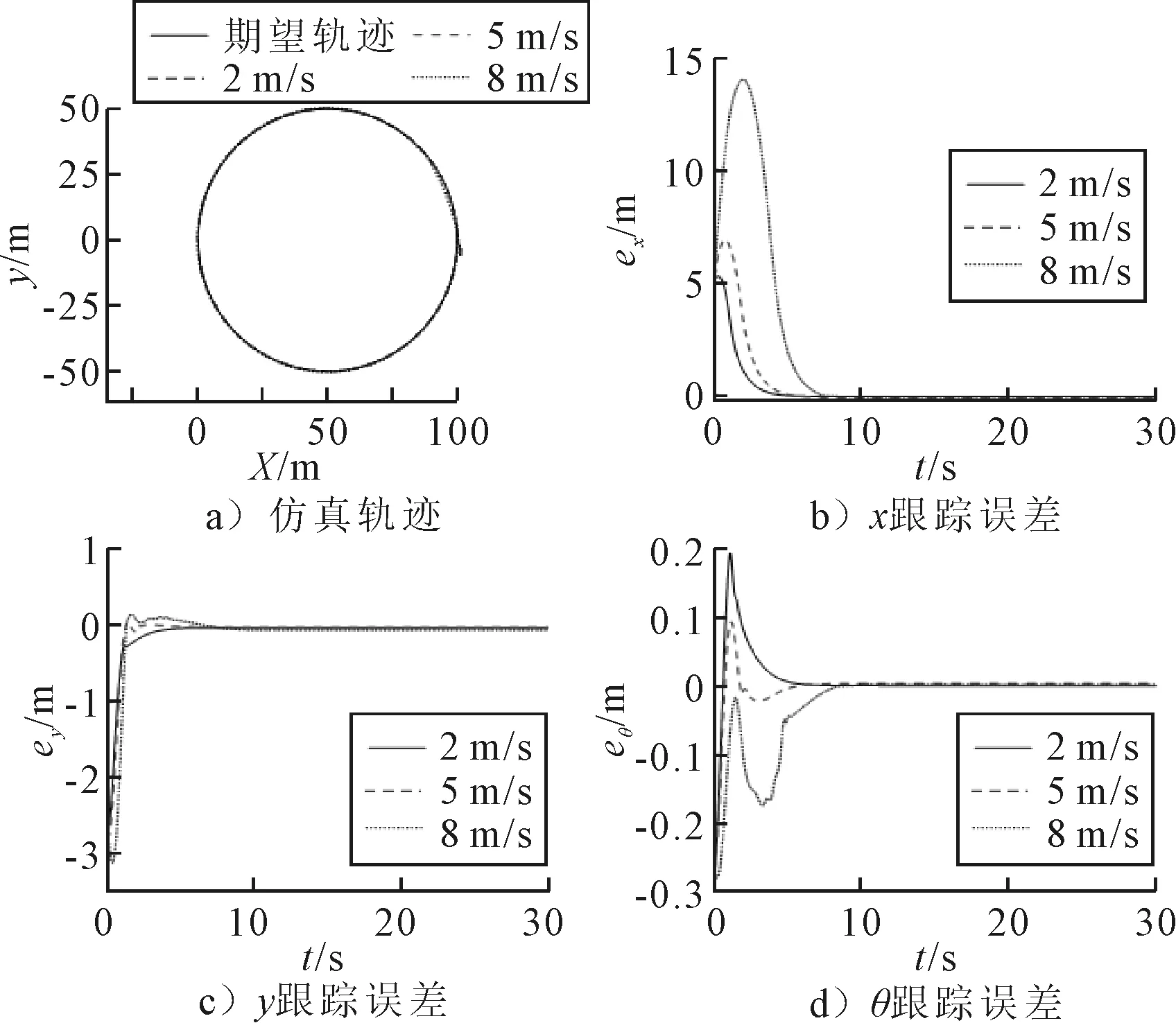
图5 仿真结果

由图5可知：文中所设计的自适应轨迹跟踪控制器在2，5和8 m/s的期望速度下运行时都能很好的跟踪目标轨迹.相比于固定参数的轨迹跟踪控制器，文中所设计的适应轨迹跟踪控制器能动态调整参数到合适的值，能让AGV快速收敛到目标曲线并稳定运行.

3.2 实验验证

AGV实验平台和实验场景见图6.AGV的实时位姿通过RTK-GNSS/IMU/码盘组合定位获得，所有控制程序均基于ROS/C++下开发.由于受实验条件的限制，实验平台的运行速度较低，因此，分别在0.5，1.0和1.5 m/s的期望速度下进行实验.车辆在全局坐标系下的初始偏差为xe=1.25 m；ye=0.22 m；θe=-π/8，初始运动状态线速度和前轮转角均为0，控制周期为0.1 s，基于上述条件AGV轨迹跟踪控实验结果见图7.

图6 AGV实验场景

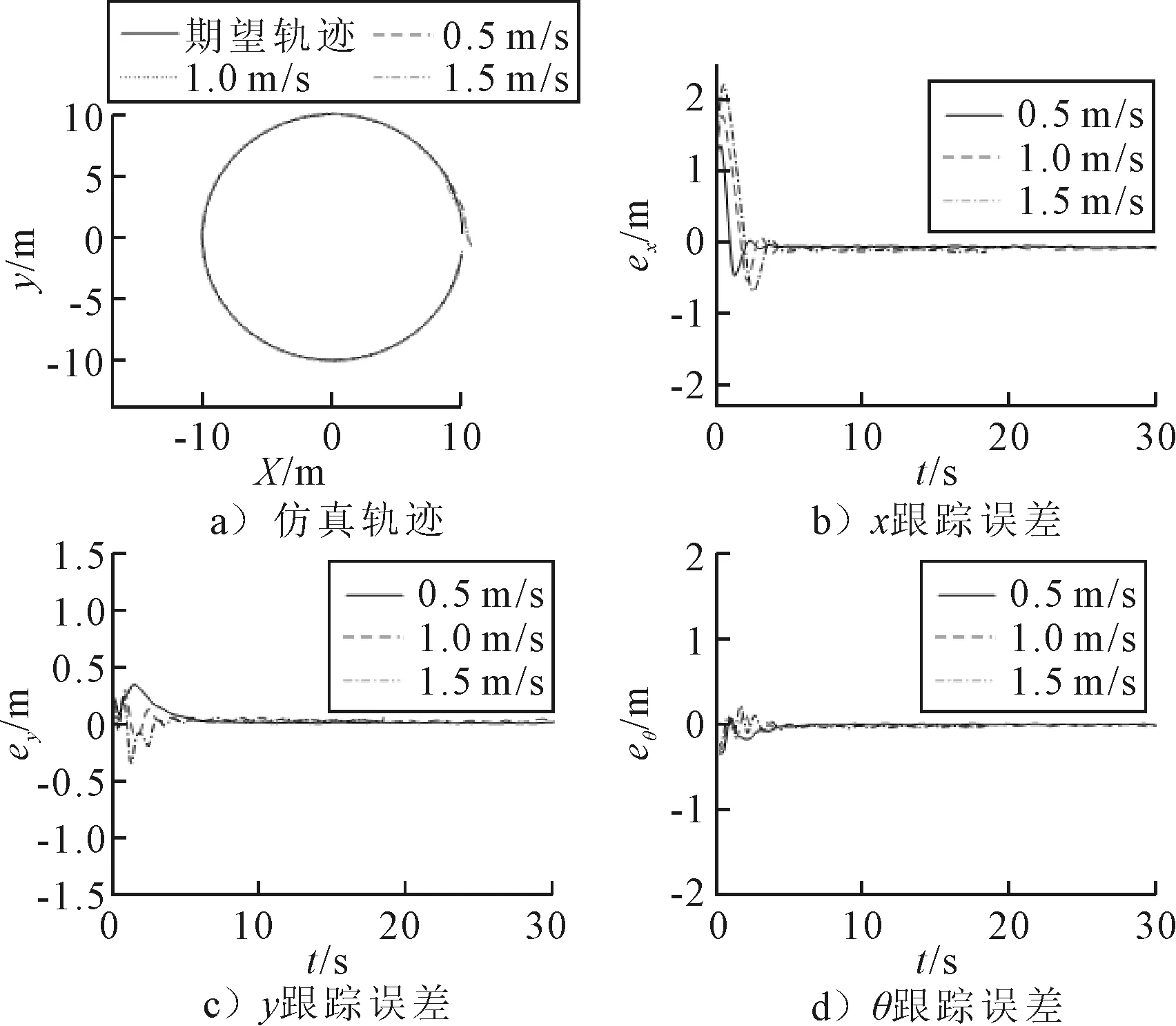
图7 实验结果

由图7可知：文中设计的自适应轨迹跟踪控制器在不同速度下都能较好的实现AGV的轨迹跟踪控制.轨迹跟踪误差都能快速收敛到0附近，但是由于实际车辆的速度响应不是很精准，误差在稳定后会有一定的稳态偏差.实验效果虽不及仿真效果，但也足以证明文中所设计的轨迹跟踪控制器在实际条件下也能很好地实现AGV的轨迹跟踪控制，具有较快的收敛速度和较强的鲁棒性.

4 结 束 语

文中根据AGV的运动学模型，推导出了其位姿误差微分方程，采用反演法设计了AGV的轨迹跟踪控制率，通过Lyapunov方法验证了其稳定性，并通过仿真实验测试了其跟踪性能；在分析了控制器中各个参数对控制器影响的基础上，设计了1个模糊控制器，根据期望跟踪速度、横向偏差和航向偏差自适应调整控制率中的参数t2和t4.搭建了Simulink-Carsim联合仿真平台和实车实验平台，仿真和实验均表明所设计的轨迹跟踪控制器能较好的实现对目标轨迹的跟踪.相比传统反演法设计的轨迹跟踪控制器，文中所设计的自适应轨迹跟踪控制器能让AGV快速收敛到目标曲线并稳定运行，且具有较强的鲁棒性和稳定性.