大悬臂预应力混凝土花瓶式桥墩预应力布置

2023-01-18胡志坚于媛媛刘欣超余顺新张申昕

武汉理工大学学报（交通科学与工程版） 2022年6期

胡志坚于媛媛刘欣超余顺新张申昕*

(武汉理工大学交通与物流工程学院1) 武汉 430063) (河北省高速公路京雄筹建处2) 雄安 071799) (中交第二公路勘察设计研究院有限公司3) 武汉 430100)

0 引言

为节省桥下空间，大悬臂花瓶式桥墩的悬臂长度往往较大，结构自重及架梁荷载会在结构上产生较大的负弯矩，使大悬臂花瓶式桥墩的顶面上产生较大的拉应力，对结构的安全性产生较大的危害[1].因此,有必要在花瓶式桥墩内设置预应力以抵消后续加载的不良影响.

大悬臂花瓶式桥墩的因其悬臂段的变截面形式，其预应力筋的布置形式与普通的等截面梁花瓶式桥墩不同[2]，针对大悬臂或变截面的结构形式，并未有一套成熟的设计理论和方法[3-4]，在预应力布置计算分析以及设计方法上仍然存在着尚未被完全理解和有效运用的问题[5-7]，给设计带来了诸多难题.

文中明确不同荷载工况下的大悬臂花瓶式桥墩的荷载效应及受力特点，并根据最小弯曲能量定理来进行预应力的相应配置优化.

1 预应力束布置公式推导

1.1 最小弯曲能量配束原理

将基于弯曲能量最小原理对大悬臂花瓶式桥墩的预应力配束进行优化配置，将预应力荷载作为平衡弯曲荷载的预加荷载，得到弯曲应变能的表达式[8]为

(1)

式中：MP为预应力产生的弯矩；Mw为除预应力荷载以外的其他荷载产生的弯矩；Ie为根据弯曲应变能等效的等截面梁抗弯惯性矩，Ie=(185c3+141c2+87c+35)I0/448，令(185c3+141c2+87c+35)/448=A，则有Ie=AI0；I0为花瓶式桥墩悬臂段悬臂根部的截面抗弯惯性矩.

大悬臂花瓶式桥墩在施工过程中主要承受结构自重、主梁架设荷载及二期恒载的作用，这些荷载均可以简化为以均布荷载或集中荷载作用在大悬臂花瓶式桥墩的形式，因此分别针对均布荷载及集中荷载的作用形式进行预应力束布置的理论推导.

1.2 均布荷载作用下的预应力束布置公式推导

大悬臂花瓶式混凝土桥墩在浇筑完成后，首先需要承担其自重荷载，自重荷载可以简化为图1的均布荷载工况.

图1 大悬臂花瓶式桥墩均布荷载示意图

将变截面段的阶梯形均布荷载等效为矩形均布荷载，公式为

(2)

式中：γ为混凝土容重；he为悬臂段等效高度.

则等效均布荷载qe为

(3)

由此计算得到均布荷载作用下的大悬臂花瓶式桥墩的弯矩图,见图2.

图2 大悬臂花瓶式桥墩弯矩图

由图2可知：大悬臂花瓶式桥墩的跨中段在均布荷载作用下，只在固定端附近区域内存在负弯矩，因此预应力配束以悬臂段作为主要的配束目标进行配束分析.

1) 均布荷载作用下的悬臂段配束计算在进行均布荷载作用下的悬臂段配束计算时，通过将弯曲荷载产生的弯曲弯矩Mw以及预应力荷载产生的平衡弯矩MP代入式(1)并求解使弯曲能量最小的预应力布置优化参数.悬臂段任意x处的弯曲弯矩Mw为

Mw1(x)=(c+2)q0x2/6

(4)

图3为均布荷载作用下悬臂段预应力束布置示意图.预应力束产生的平衡弯矩MP主要由其偏心距决定，花瓶式桥墩盖梁在悬臂端部并不需要很大的预压应力，并且端部预应力效应过大同样会导致在悬臂下缘产生较大的拉应力，因此在悬臂端部减小预应力钢束的偏心矩，预应力束在端部距截面中性轴的距离为H1/2-h1-h2，并且使预应力束的偏心距e1(x)由端部至根部逐渐增加，并在悬臂根部达到最大值，此时预应力产生的预压弯矩也达到最大值，预应力束距悬臂根顶部的距离为h2，悬臂根部的偏心距为e0，任一点处的偏心距e1(x)为

e1(x)=(e0-(L1-x)·h1/L1)

(5)

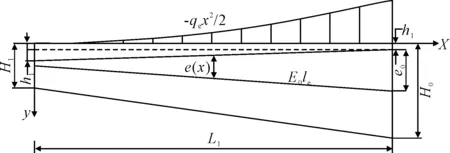
图3 均布荷载作用下悬臂段预应力束布置示意图

均布荷载作用下悬臂段的弯曲应变能：

(6)

式中：α为考虑结构压应力储备的安全系数，下同.

将f(x)在悬臂段上积分，得到F表达式为

(7)

由弯曲能量最小原理，通过对h1求偏导，并令∂F/∂h1=0可以得到：

(8)

(9)

在确定h1与h2后，均布荷载作用下的悬臂段预应力的布置形式也就随之确定.

2) 均布荷载作用下的跨中段配束计算大悬臂花瓶式桥墩跨中段在固定端区域负弯矩，见图4.

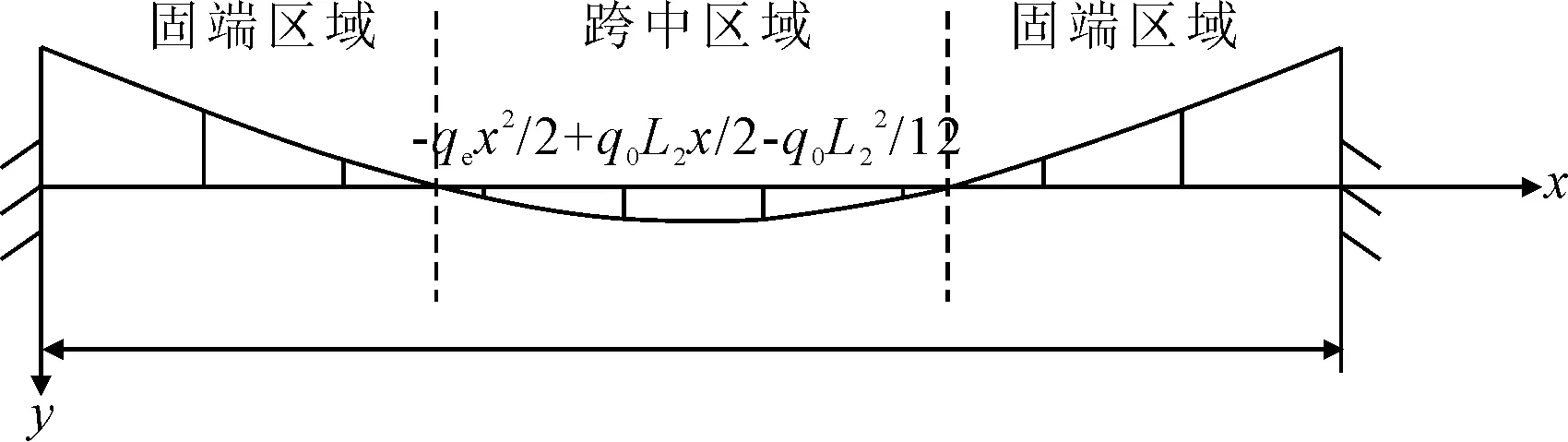
图4 均布荷载作用下跨中段弯矩图

在跨中段的跨中区域，因为正弯矩的存在，这一区域的偏心距可以设置的较小；跨中段固端的负弯矩沿着x轴不断减小，对应地将预应力束由根部的h2位置向下布置过渡至跨中区域布置，偏心距由固端的e0过渡至弯矩为0位置的e2，并在跨中区域保持不变，跨中段预应力束的布置形式见图5.

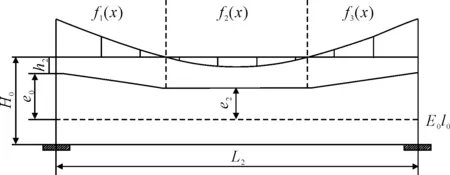
图5 大悬臂花瓶式桥墩跨中段预应力布置示意图

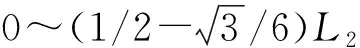
(10)

(11)

2EI0)2dx

(12)

跨中段总弯曲应变能F(x)=f1(x)+f2(x)+f3(x)，将F(x)在整个跨中段区域上积分，然后对e2求偏导，并令∂F/∂e2=0可以求得：

(13)

1.3 集中荷载作用下的预应力束布置公式推导

1) 集中荷载作用下的悬臂段配束计算大悬臂花瓶式桥墩承担其自重荷载后，将进行上部预制T梁的架设，等同于在花瓶式桥墩的相应临时支座位置施加集中荷载，在完成T梁架设，进行桥面铺装时，二期恒载也以集中荷载的形式通过主梁及临时支座作用在盖梁上，对应这两种工况进行集中荷载作用下的悬臂段预应力束布置公式推导.

盖梁在集中荷载作用的弯矩图见图6.

图6 大悬臂花瓶式桥墩集中荷载作用弯矩图

对悬臂段的预应力束布置进行计算，集中荷载作用下的预应力束布置见图7.

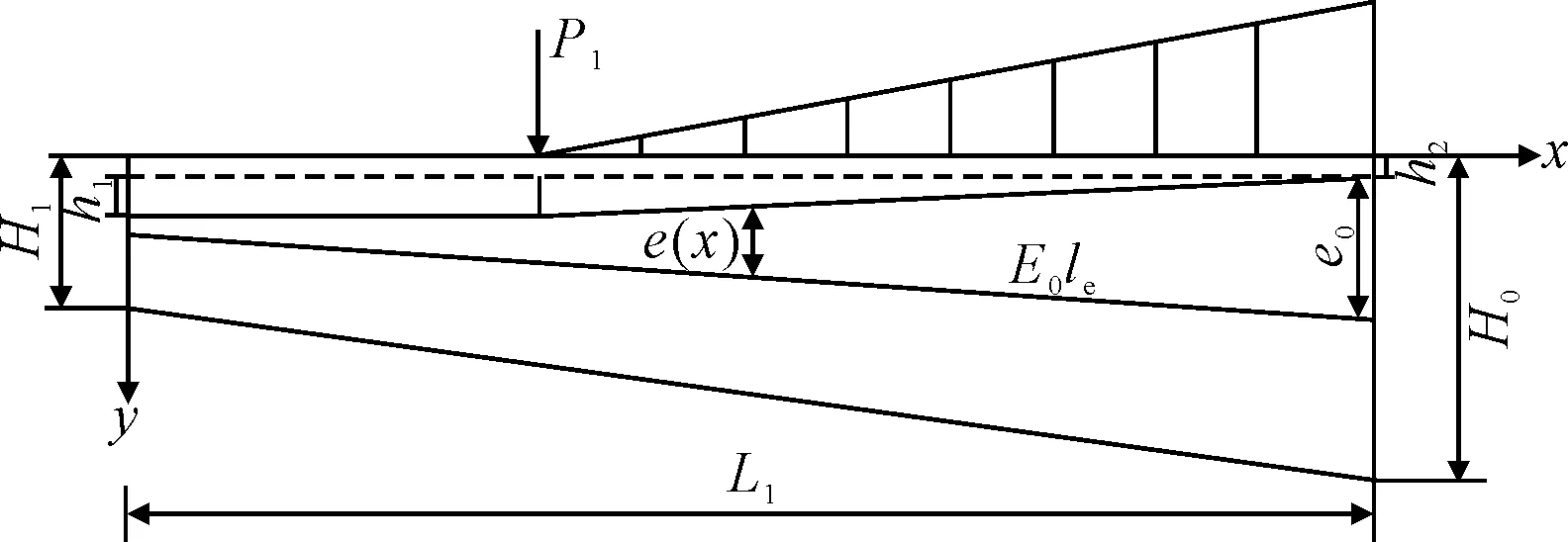
图7 集中荷载作用下的悬臂段预应力束布置

对悬臂段的弯曲弯矩Mw进行计算，在集中荷载作用下，悬臂段的弯矩由集中荷载作用点至悬臂根部逐渐增大，任意x处的弯矩为

“工学结合，校企融合”的特点是在企业工作中学习。受社会其他思想和价值观影响，大学生思政教育不断产生新问题。辅导员和思想政治课教师要提前对学生可能面临的问题正确预测，分析企业环境带给学生的正负面影响，防患于未然。

(14)

在悬臂端部至集中荷载作用位置，弯曲弯矩为0，这一段的预应力束水平布置，在集中荷载作用位置至悬臂根部，预应力束根据集中荷载引起的弯矩相应靠上布置，偏心距在悬臂根部达到最大值e0，此时预应力束距悬臂根顶部的距离为h2，悬臂段预应力束任一点处的偏心距e1(x)为

e(x)=h1(((L1-a1)-x)/(L1-a1))

(15)

弯曲应变能f1(x)、f2(x)根据跨中段的预应力束的段布置分别进行推导.0～a1区域内，悬臂段弯曲应变能f1(x)为

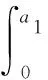
(16)

a1～L1区域内，悬臂段弯曲应变能f2(x)为

f2(x)=

(17)

由此得到跨中段总弯曲应变能F(x)在整个悬臂段区域上积分并求h1偏导，令∂F/∂h1=0可以求得：

(18)

2) 集中荷载作用下的跨中段配束计算盖梁在集中荷载作用下，跨中段弯矩由固定端负弯矩过渡为正弯矩，在集中荷载作用位置达到正弯矩最大值，跨中段任意x处的弯曲弯矩Mw为

(19)

跨中段预应力束的布置形式见图8.

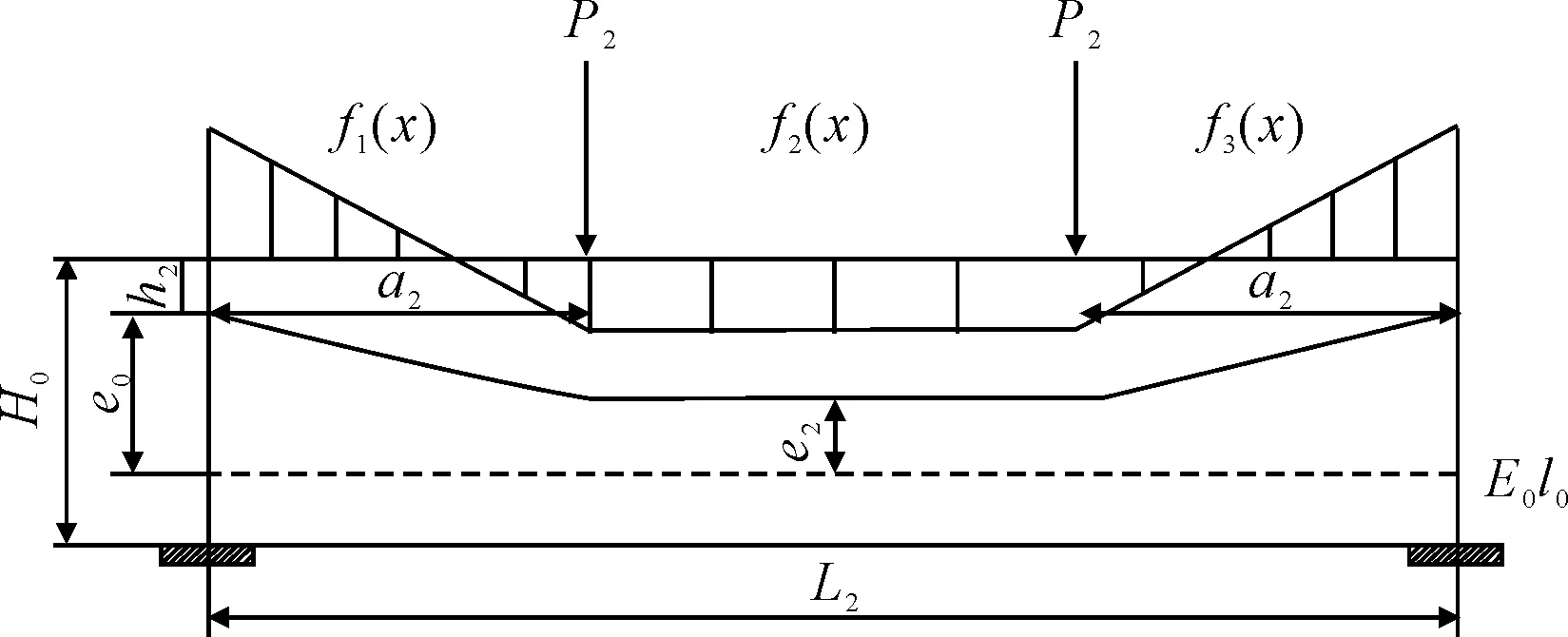
图8 集中荷载作用下的跨中段预应力束布置

跨中段的弯曲应变能公式f1(x)、f2(x)、f3(x)随预应力束的三段布置分别推导，其中0至a2固端区域内，跨中段弯曲应变能f1(x)为

(20)

a2～(L2-a2)跨中区域内，跨中段弯曲应变能f2(x)为

(21)

(L2-a2)～L2固端区域内，跨中段弯曲应变能f3(x)为

(22)

将跨中段总弯曲应变能F(x)=f1(x)+f2(x)+f3(x)在整个跨中段区域上积分并对e2求偏导，令∂F/∂e2=0可以求得：

(23)

1.4 大悬臂花瓶式桥墩预应力配束计算流程

求解大悬臂花瓶式桥墩预应力配束参数的具体计算步骤为：

步骤2确定均布荷载下的悬臂段根部预应力束至顶部距离h2、根据式(9)计算端部配束参数h1.

步骤3计算均布荷载作用下跨中段弯矩为0的位置，确定预应力束弯折点，根据式(13)计算对应的跨中段配束参数e2.

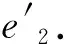
步骤6计算二期恒载对应配束参数.

2 理论预应力束优化布置实例

2.1 工程概况

京雄高速KT8标段采用大悬臂花瓶式桥墩盖梁长度为33.6 m，花瓶式桥墩盖梁C50混凝土容重γ=25 kg/m3，其中悬臂段长度L1=11.8 m，跨中段长度L2=10 m，盖梁采用宽度为2.5 m的矩形截面，截面高度由悬臂端部H1=1.5 m过渡至悬臂根部H2=1.5 m,具体大悬臂花瓶式桥墩构造尺寸图见图9.

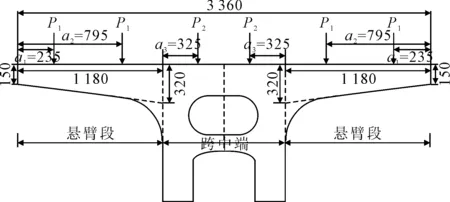
图9 大悬臂花瓶式桥墩构造尺寸图(单位：cm)

2.2 预应力束布置参数计算

花瓶式桥墩共布置三排张拉控制应力N=3 684.2 kN的19×15.2预应力钢绞线，布置见图10.

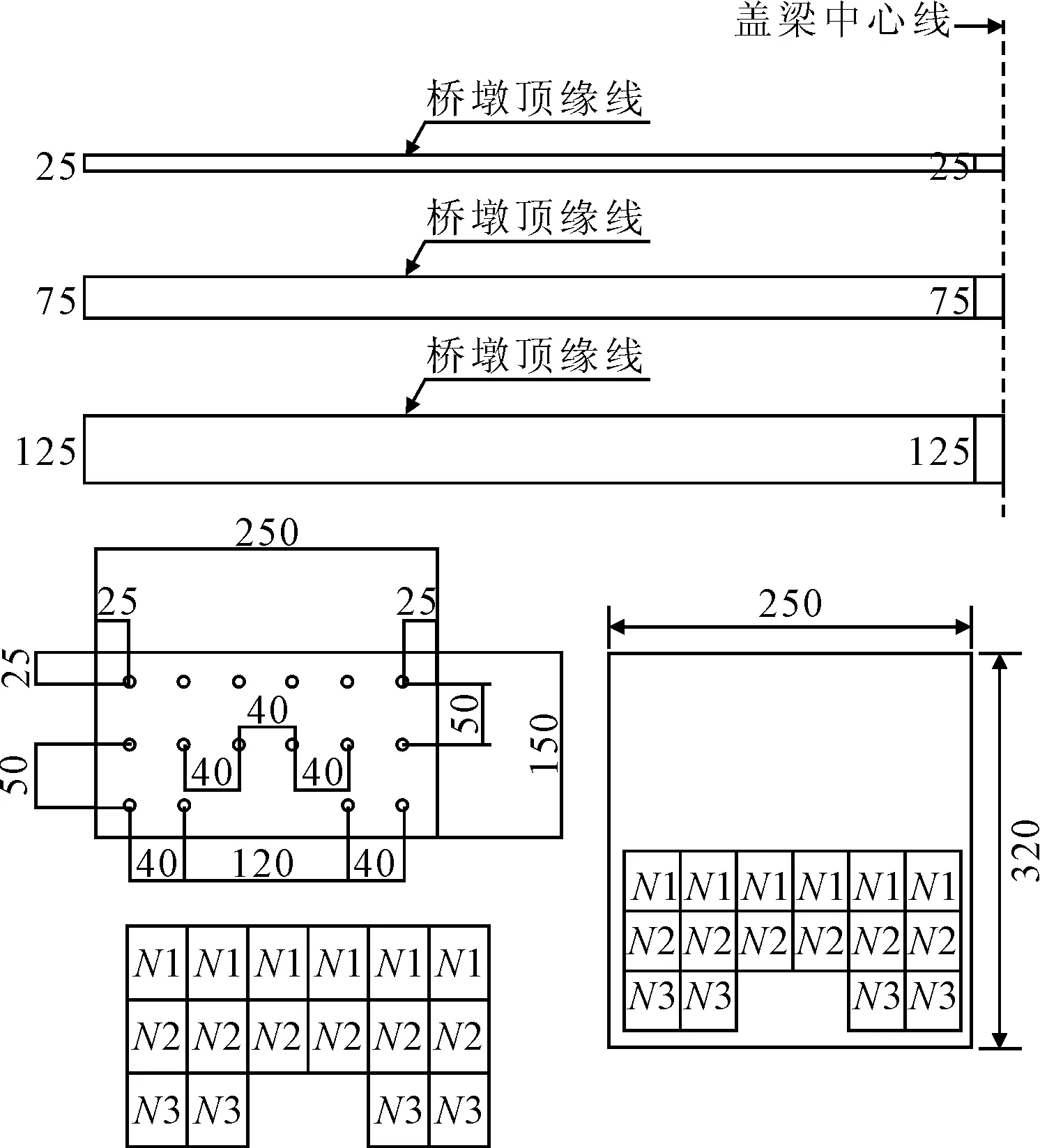
图10 大悬臂花瓶式桥墩预应力束布置图(单位：cm)

大悬臂花瓶式桥墩施工过程中的自重荷载、主梁架设荷载、二期恒载都是分阶段施加的，预应力钢束对应的根据预压弯矩抵消设计荷载效应并提供一定的预压应力储备的原则分批张拉.施工完成后，所有的预应力束也应共同作用抵消长期荷载及短期荷载组合下的弯曲弯矩，使结构保持在安全的受力状态下.

因此利用理论配束公式对大悬臂花瓶式桥墩进行预应力配束计算时，在考虑三排预应力束共同抵消荷载效应并提供预应力储备的前提下，分别根据不同施工阶段的荷载工况，使用均布荷载及集中荷载作用下的配束公式对N1、N2、N3预应力束的配束计算，使其抵消设计荷载效应并提供预压力储备，并最终考察N1、N2、N3预应力束共同作用下的结构受力状态.

表1为预应力束N3的计算参数，预应力束N3布置见图11.

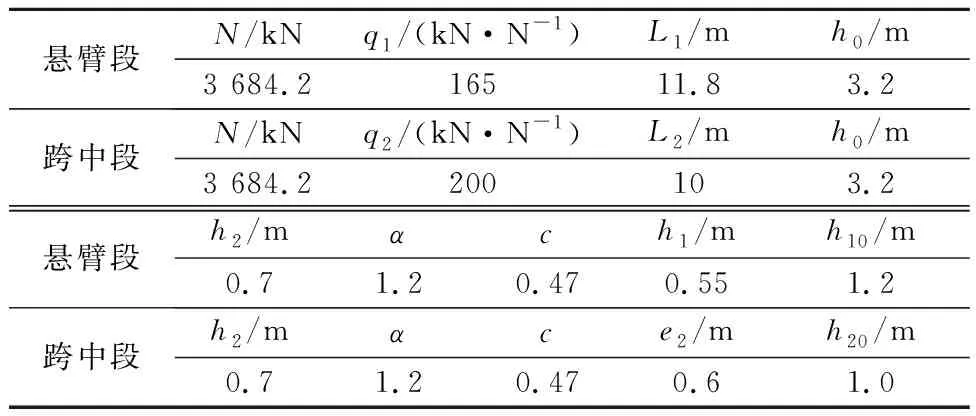
表1 预应力束N3计算参数表

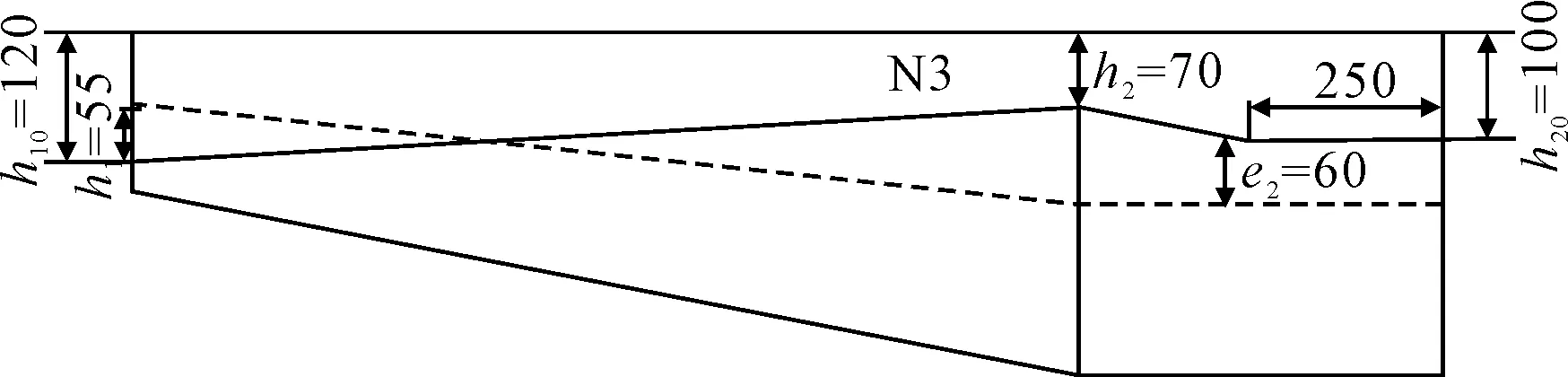
图11 预应力钢束N3布置图(单位：cm)

表2为N2预应力钢束的计算参数，预应力束N2布置见图12.

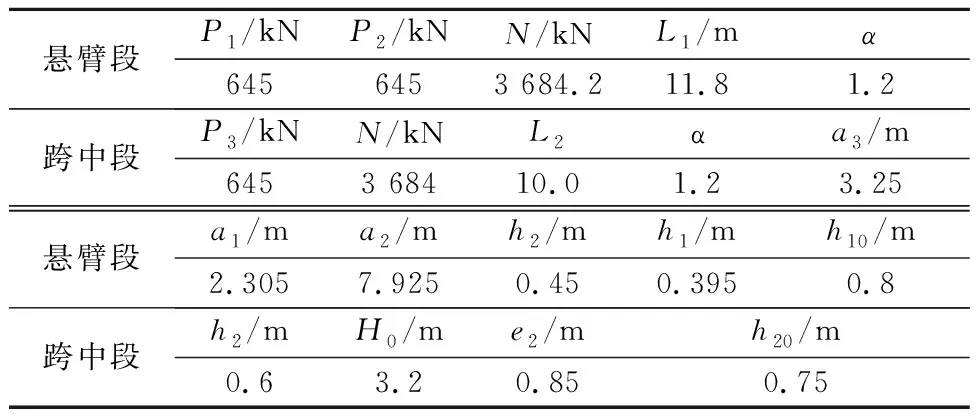
表2 预应力束N2计算参数表

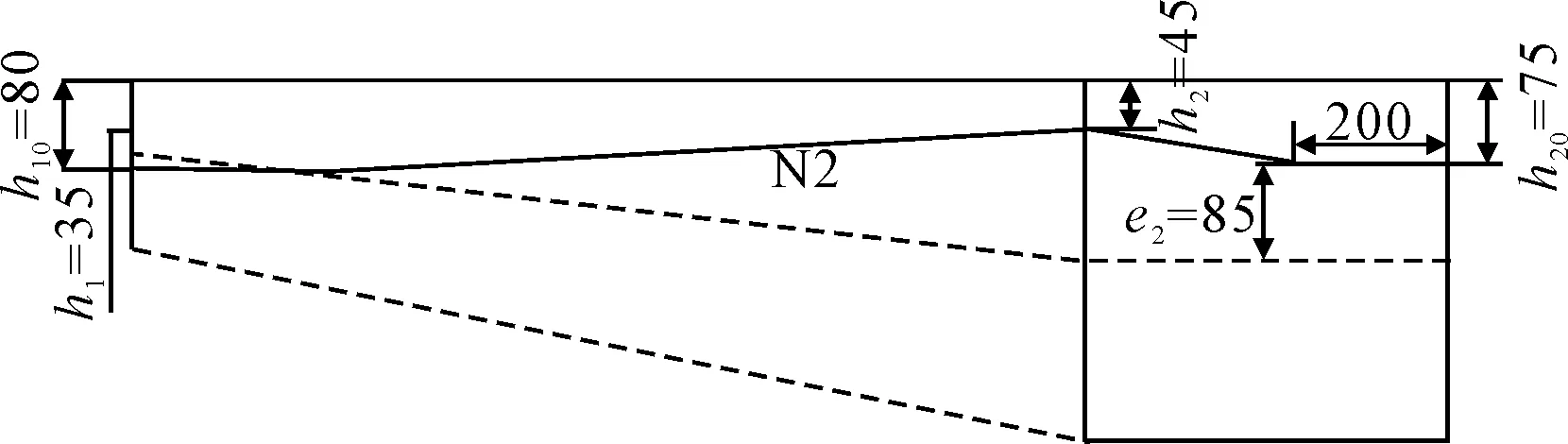
图12 预应力钢束N2布置图(单位：cm)

表3为N1预应力钢束的计算参数，第一排的预应力钢束N1布置见图13.

表3 预应力束N1计算参数表

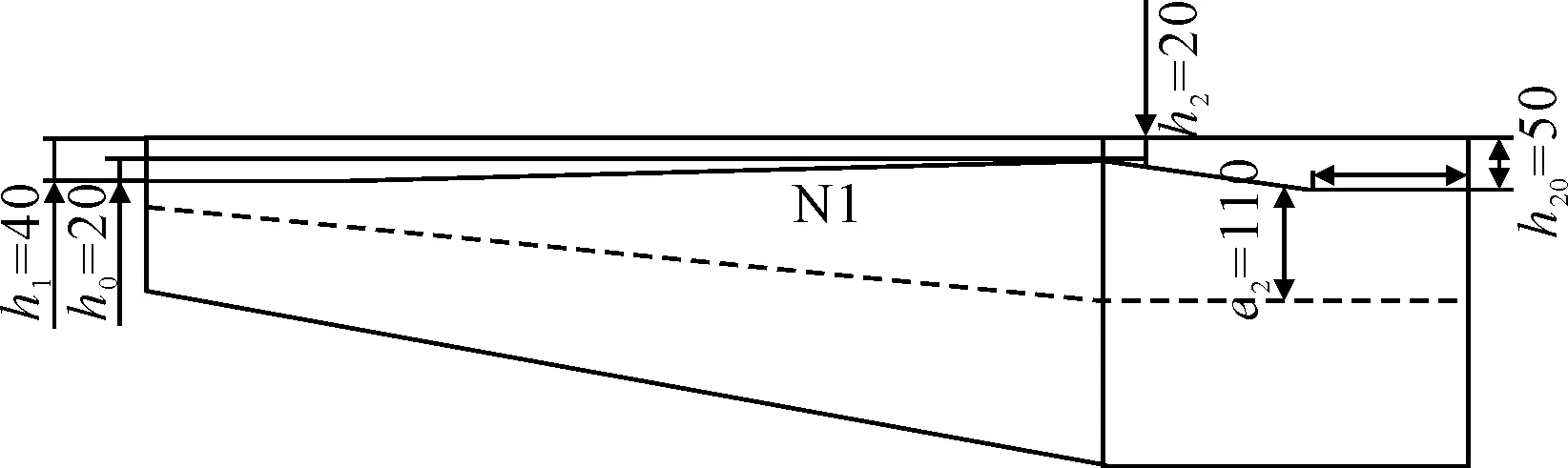
图13 预应力钢束N1布置图(单位：cm)

3 理论计算配束的有效性验证

3.1 理论配束有限元模型建立

通过2.2的计算，并结合实际的工程布置，得到了图14的理论计算预应力束布置，为了验证该预应力束布置的有效性，应用ANSYS建立该理论计算预应力束布置的大悬臂花瓶式桥墩有限元模型，并进行加载计算.

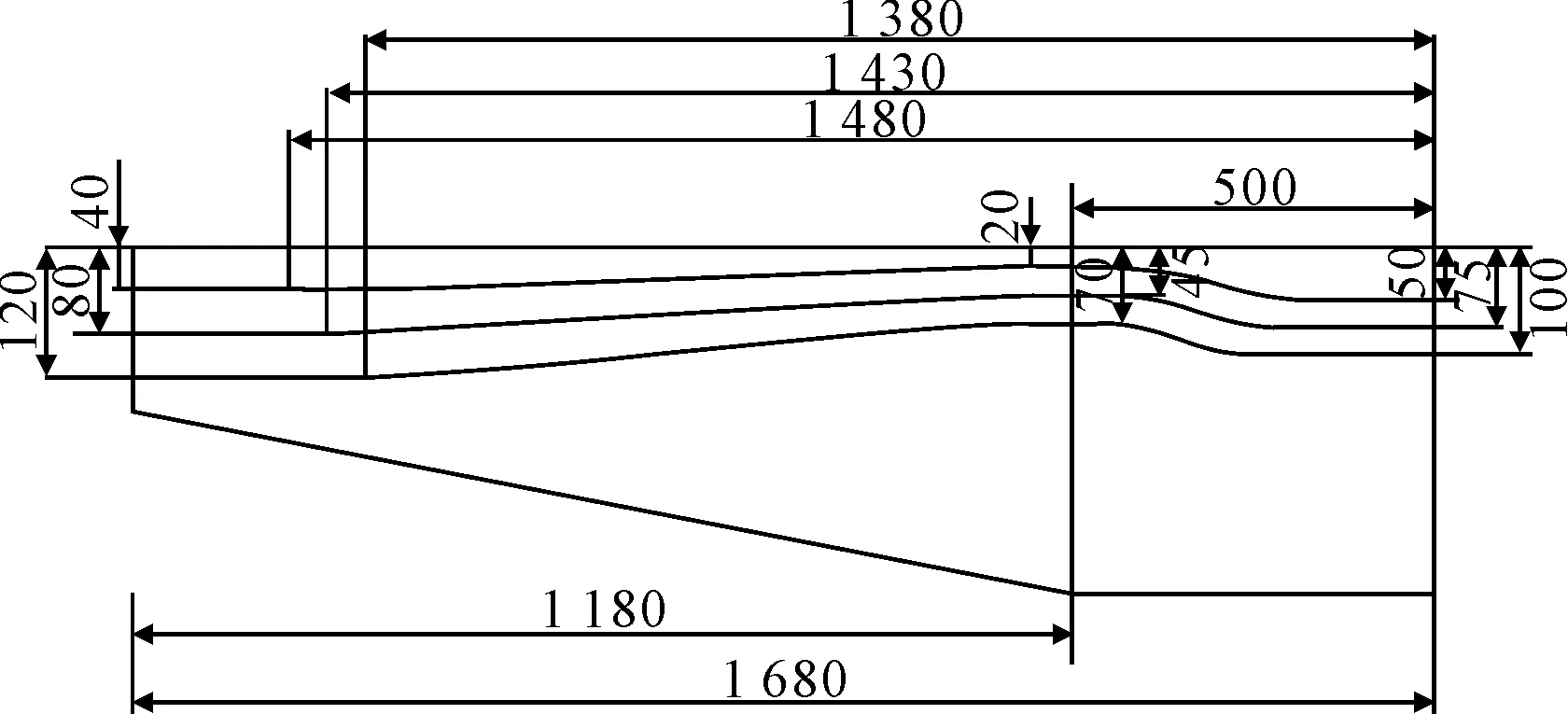
图14 理论计算预应力钢束布置(单位：cm)

在建立花瓶式桥墩钢筋混凝土有限元模型时，分别采用Link8单元与Solid65单元来模拟预应力筋与混凝土，利用Solid65单元的实常数，通过对盖梁划分区域保证区域内三向配筋率相同的原理，来模拟盖梁的普通钢筋.Link8单元则与混凝土进行映射网格划分，并将节点耦合，通过对Link8单元施加初应变来模拟预应力束张拉并对混凝土施加预压应力的过程.建立的大悬臂花瓶式桥墩有限元模型见图15.

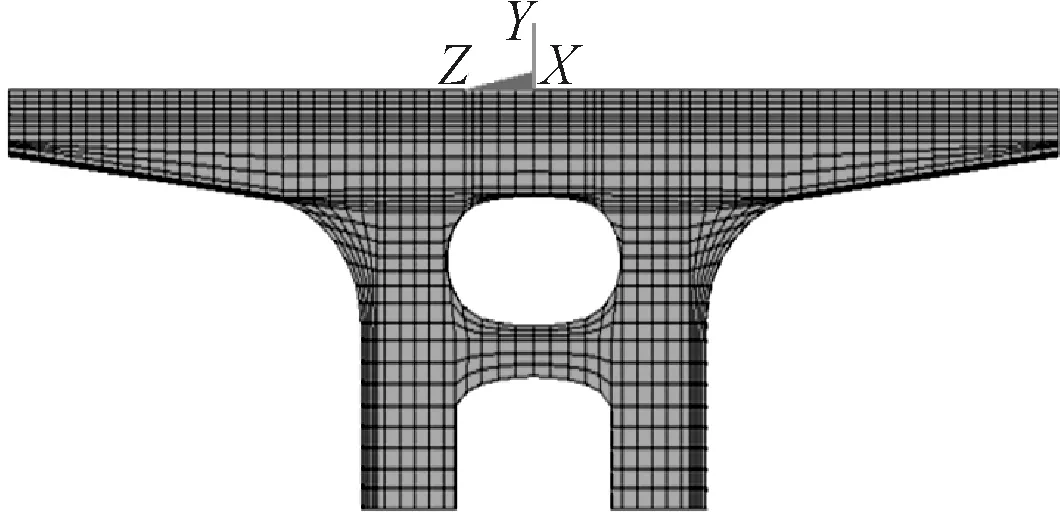
图15 花瓶式桥墩有限元模型

3.2 理论计算配束的有效性验证

提取预应力束N3张拉及设计荷载施加工况的顶面及底面节点的应力位移结果，见图16.

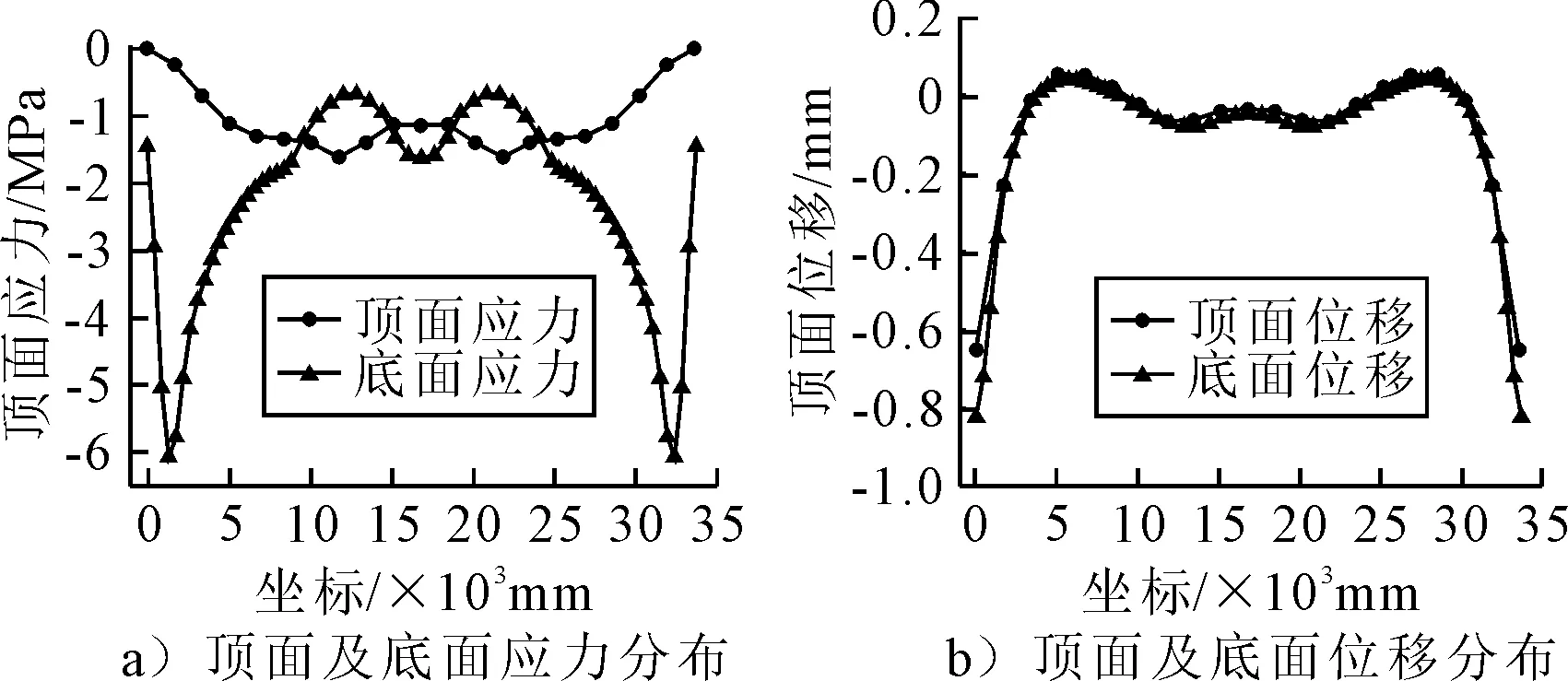
图16 预应力束N3张拉有限元受力情况

由图16可知：在预应力钢束N3张拉后，花瓶式桥墩盖梁顶面并未出现拉应力，在5～25 m范围，盖梁顶面压应力分布较为均匀，而顶面位移也与应力分布规律相对应，在该范围内顶面与底面位移均较小，接近于0.由花瓶式桥墩盖梁底面应力可以看出，底面均未出现拉应力，预应力束N3并不存在预应力过大的情况.

提取预应力束N2张拉及设计荷载施加工况下的结构顶面及底面的应力位移结果，见图17.

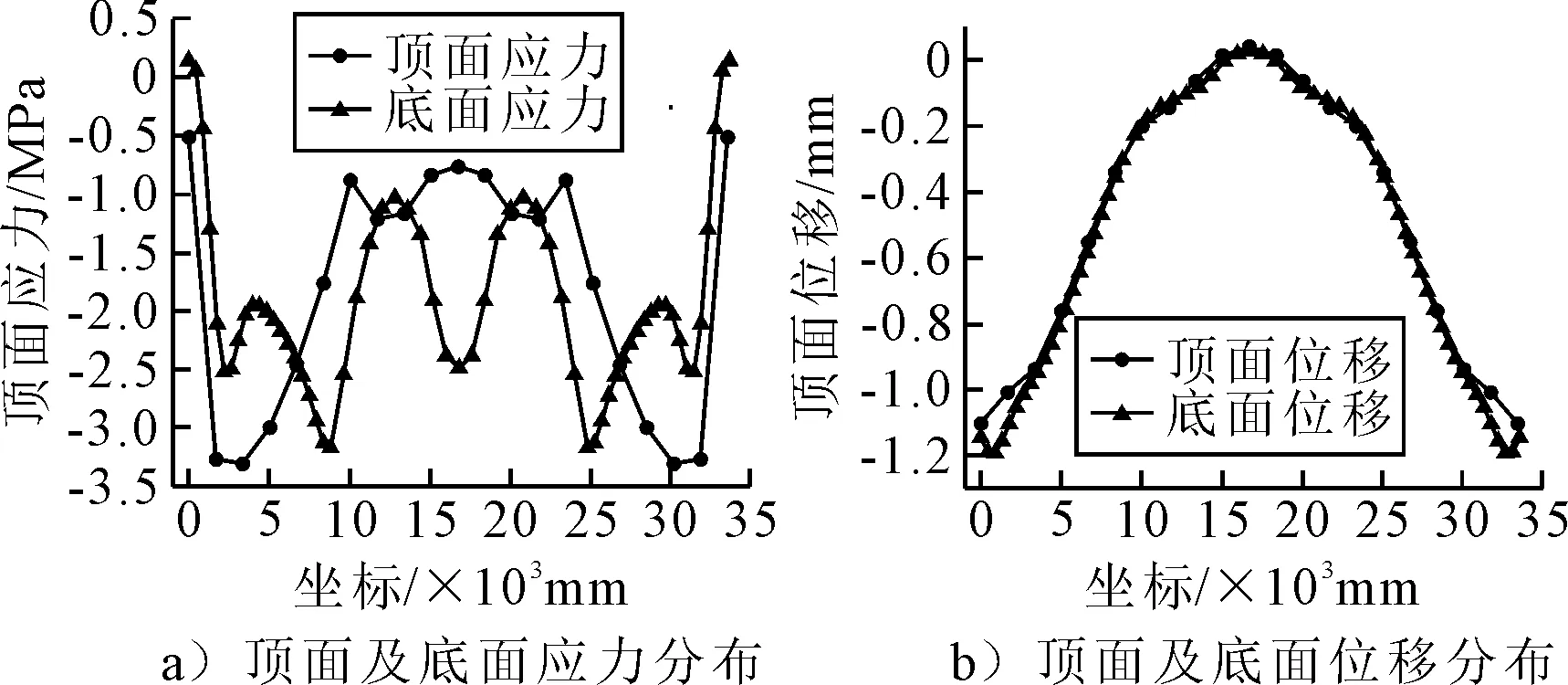
图17 预应力束N2张拉有限元受力情况

由图17可知：在设计荷载作用下，预应力钢束N2张拉后，花瓶式桥墩盖梁顶面及底面基本未出现拉应力，整体结构处于受压状态，且顶面应力数值与底面应力数值较为接近，说明整个截面上的应力分布较为均匀，中性轴变形较小，符合配束时弯曲应变能最小的准则.由顶面及底面位移图可以看出，花瓶式桥墩盖梁整体位移呈下挠趋，预应力束N2并不存在预应力过大的情况.

提取预应力束N1张拉及设计荷载施加工况下的结构顶面及底面的应力位移结果，见图18.

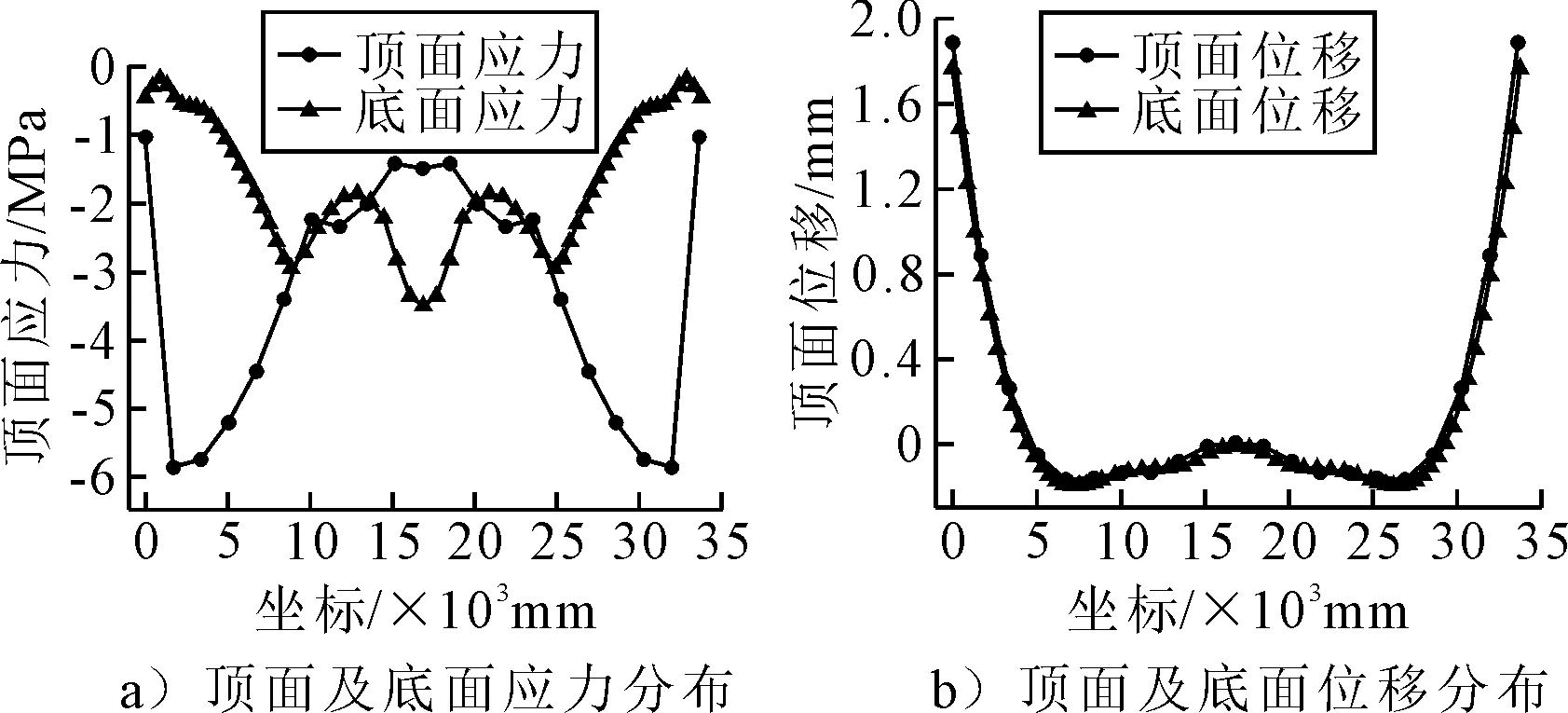
图18 预应力束N1张拉有限元受力情况

由图18可知：在预应力钢束N1张拉后，花瓶式桥墩盖梁顶面及底面基本未出现拉应力，整体结构处于受压状态，且在悬臂段具有较大的压应力储备，因为跨中段采用了三段式布置，因此在跨中的顶面及底面应力曲线上也呈三段式分布，增加了底面的压应力储备，防止了后续开裂风险.

对预应力束N1、N2、N3在花瓶式桥墩施工完成后，共同作用对长期荷载及短期荷载效应组合的荷载效应的抵消情况，提取结构的顶底面应力及位移，分别绘制应力作用效果及位移作用效果图见图19.

图19 理论配束整体作用效果

由图19可知：预应力束N1、N2、N3整体作用下很好地抵消了花瓶式桥墩的荷载效应，且未出现预应力较大的情况，同时结构的顶面及底面均具有一定的压应力储备，保证了结构的安全性.通过理论计算进行的预应力配束是有效的.

3.3 理论计算配束与原型配束对比

利用相同的建模方法分别建立理论配束及原型桥墩的ANSYS有限元模型，按照实际的施工及预应力张拉顺序进行加载，在完成全部运算后，提取理论配束及原型桥墩顶面及底面的节点应力、位移数据，见图20.

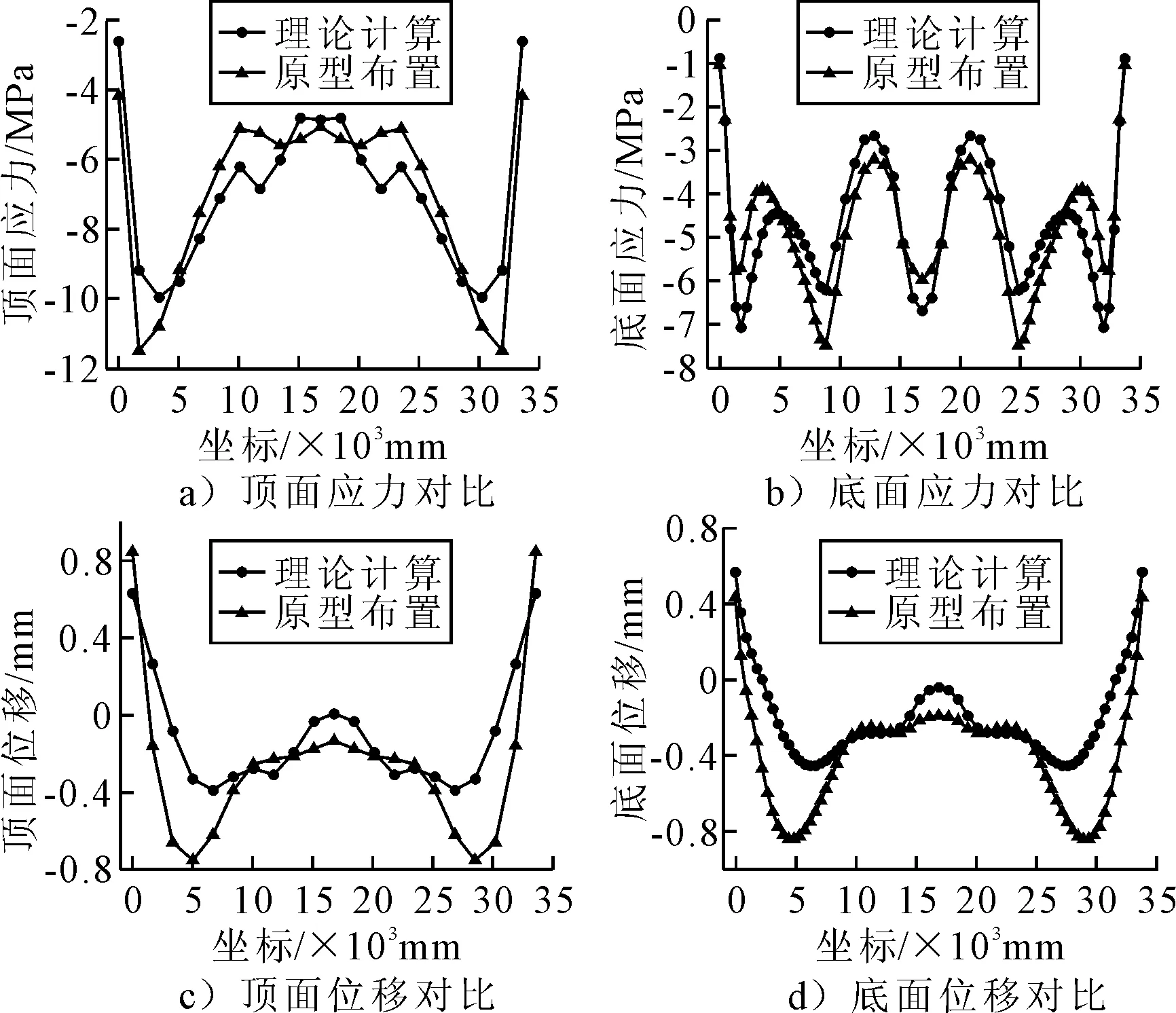
图20 理论配束与原型桥墩顶底面应力及位移结果对比

由图20可知：虽然理论配束相较原型桥墩的顶面最大压应力值(10 MPa)要小于原型桥墩的最大压应力值(12 MPa)，但其压应力储备已经保证了结构后续的安全性，并且理论配束的顶面及底面整体应力分布更为均匀，符合其弯曲应变能最小的设计原则.同时由于理论配束在悬臂段采用靠上配束不断增加偏心距的设计，理论配束在悬臂根部这一危险截面的顶面压应力值要大于原型桥墩，整体的应力分布更为合理.位移同理.