基于视觉原理的齿轮参数测量方法研究

2023-01-17李捷刘永李昊泽姜都王宸龚立雄

工具技术 2022年10期

李捷，刘永，李昊泽，姜都，王宸，龚立雄

1湖北汽车工业学院机械工程学院；2湖北工业大学机械工程学院

1 引言

齿轮是工业生产中重要零件之一[1]，广泛应用于汽车制造[2]、航空航天及交通运输等领域。随着现代精密测量技术的快速发展，传统的测量设备已经无法满足现代化工业生产中快速、准确测量齿轮参数和误差的要求。

机器视觉作为一种快速发展的检测手段，具有低成本、对零件表面无损伤和效率高等优点。目前，较多国内外学者对机器视觉测量齿轮参数及误差方法进行了研究。文献[3，4]通过设置掩模模板并统计连通域个数来计算齿数，计算量较大，操作较为复杂；文献[5-7]为了得到齿轮边缘图像，利用Canny算子提取边缘，Canny算子是像素级别的边缘检测算子，而像素级边缘检测已经无法满足图像测量的要求；文献[8]提取了齿顶、齿根部分圆弧曲线，利用最小二乘法拟合求出齿顶和齿根圆半径，该方法测量结果容易受到圆弧曲线提取效果的影响，当存在加工误差时，圆弧部分曲线会存在一定误差，导致测量结果出现偏差。

本文提出一种基于视觉原理的齿轮参数和齿距、齿厚误差测量方法。通过工业相机采集齿轮图像后，提取图像亚像素边缘轮廓，设计了一系列相关算法对齿轮几何参数和齿廓、齿厚偏差进行测量，并通过实验验证测量结果。

2 齿轮测量系统

2.1 测量系统

视觉测量系统[9，10]整体结构如图1所示。主要包括CCD工业相机、工业镜头、物距和水平调节机构、环形光源、工作台和计算机。CCD工业相机分辨率为1280pixels×960pixels，覆盖1.4×107pixels。镜头为BT-MPX系列，具有高锐度、低场曲及低畸变等特点。工作台可通过步进电机驱动转动，细分后的步距角为0.12°。其工作原理为：对测量系统进行标定后，通过调节物距和水平调节结构以及工作台转动角度来调整相机、环形光源和齿轮的相对位置，以保证三者的中心一致。

图1 测量系统结构

采集完齿轮图像后，采用MATLAB软件对图像进行预处理。为了减少噪声对测量结果的干扰，利用中值滤波滤除图像中的噪声。采用Zernike矩[11]提取齿轮亚像素边缘，利用边界跟踪函数获取齿轮中心孔及齿廓边缘点的坐标信息，最后设计相关算法完成几何参数和齿距、齿厚偏差测量。测量流程如图2所示。

图2 测量流程

2.2 像素当量标定

为了得到齿轮实际参数尺寸，需要标定出实际尺寸与像素尺寸之间的比例关系。在视觉测量中得到齿轮的像素数目，需要标定出像素当量，即每个像素所代表的实际距离。本文采用高精度圆形标定板进行像素当量标定[12]，标定板尺寸如图3所示。

标定流程如图4所示。拍摄标定板图像，经过Canny算子得到标定板边缘图像，利用Zernike矩提取标定板亚像素边缘。选择圆形阵列中四个顶点和中心点，利用最小二乘法拟合得到五个点直径的像素值，计算得到五个像素当量，求其均值得到最终的像素当量K为0.0789mm/pixel，可表示为

(1)

式中，K为像素当量；L为标定板圆形阵列直径设计值；N为标定板圆形阵列直径像素个数；n为选取圆点个数。

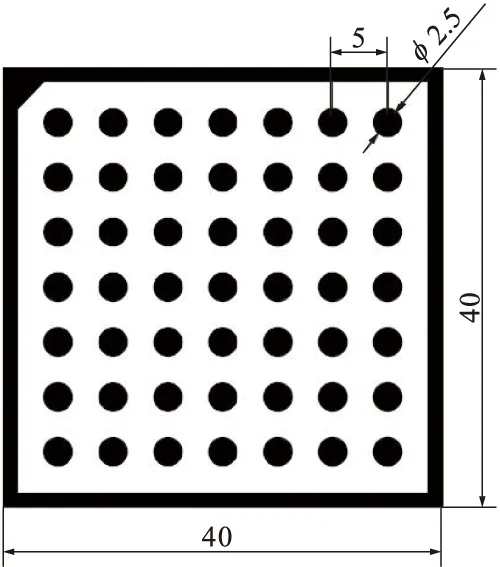
图3 圆形标定板尺寸

图4 标定过程

2.3 重复性精度验证

拍摄过程会受到外界因素影响，为了验证测量结果的稳定性，采用上述高精度圆形标定板进行重复性精度验证[13]。提取圆形阵列中四个顶点和中心点的亚像素边缘，利用最小二乘法拟合得到其圆心坐标，重复测量十次后，采用贝塞尔公式得到其标准差σi和不确定度ΔXi，有

(2)

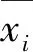
有

(3)

其标准差σi和不确定度ΔXi为

(4)

(5)

式中，σi为第i个点验证n次的标准差；ΔXi为第i个点验证n次的不确定度；tα(n-1)为自由度n-1显著水平α下的t分布置信因子。

3 齿轮基本几何参数测量

3.1 齿轮几何中心和中心孔半径

齿轮的几何中心和中心孔是加工齿轮及测量其他参数的基准，因此需要确定齿轮的几何中心。最小二乘法和重心法是常用的测量几何中心的方法，由于齿轮存在键槽，所以选择最小二乘法。提取中心孔圆弧部分亚像素边缘，利用最小二乘法拟合圆弧曲线得到几何中心和中心孔半径。

3.2 齿顶、齿根圆半径和齿数

计算所有轮廓点到齿轮中心点的距离，分别提取最大值和最小值各50个，并计算其平均值，即可得到齿顶和齿根圆半径。测量齿数需要用到上述齿廓边缘点到中心点的距离。相关的曲线分布如图5所示。

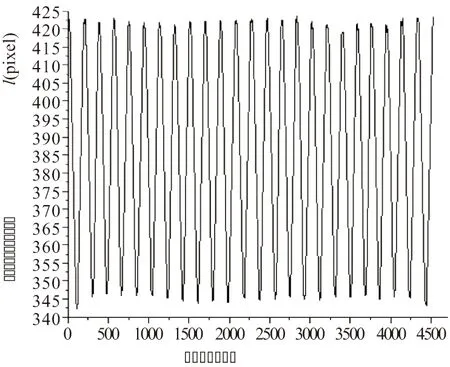
图5 齿廓边缘点到中心点的距离

图5中横坐标为齿廓边缘像素点的排列序号，纵坐标为各个点到中心点的距离值。理想状况下，齿廓边缘点到中心点的距离呈理想的周期变化，但由于齿轮加工过程中存在一定的误差，图像中齿顶和齿根部分所有点并不分别在同一高度。测量齿数时为了避免误差干扰，选取齿顶圆与齿根圆半径和的均值，在上述图像中对应高度绘制一条直线，统计直线与图像中曲线交点数，计算后即可得到齿数。

3.3 模数和分度圆直径

模数与分度圆直径均间接计算得到。根据模数m、齿数z和齿顶圆半径da之间的关系，利用式(6)计算出一个模数值，并与国际标准中模数值进行比较，从而得到最终的模数值m。

(6)

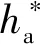
齿数z、模数m和分度圆直径d之间的关系为

d=mz

(7)

式中，z为齿数；m为模数。

4 齿距偏差与齿厚偏差

4.1 齿距偏差

齿距偏差是齿轮端面内分度圆轮廓上理论齿距与实际齿距之间的偏差。齿距偏差体现了齿轮工作时的平稳性。测量出分度圆半径值，利用齿廓边缘点到中心点距离图像与分度圆半径可得分度圆与齿廓边缘的交点信息，根据坐标信息可计算得到实际齿距，与理论齿距进行比较最终得到齿距偏差。

测量齿距偏差过程中最重要的是测量齿距，绘制出齿廓边缘点到中心点的距离图像后，以分度圆半径在上述距离图像中绘制出数值相对应的直线，即可得到分度圆与齿廓的所有交点序列(见图6)。

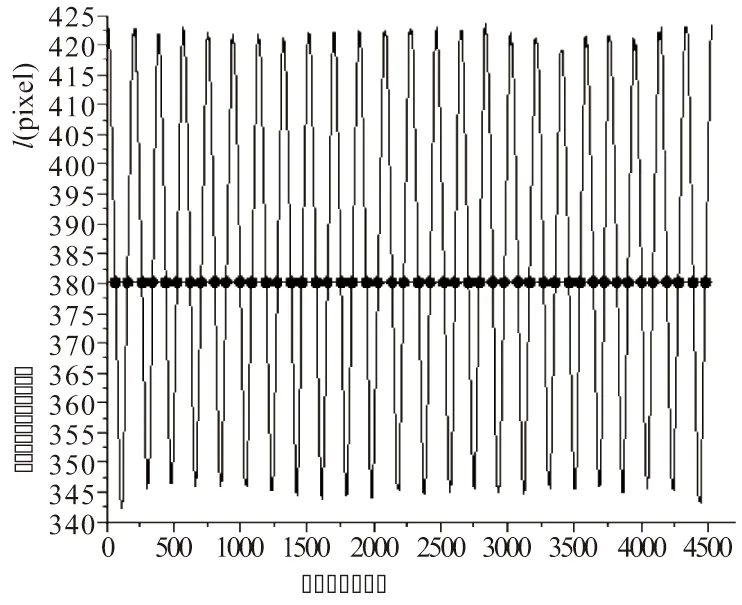
图6 分度圆与齿廓交交点序列

如图7所示，根据此序列在矩阵中提取出所有交点坐标，将交点分为左右两个齿廓交点(L1，L2，L3，…，Ln和R1，R2，R3，…，Rn)，左右相邻交点和圆心之间的角度分别为∠LiOLi+1和∠RiORi+1，根据交点坐标和夹角计算得到夹角所对应的劣弧弧长，即为齿距p。

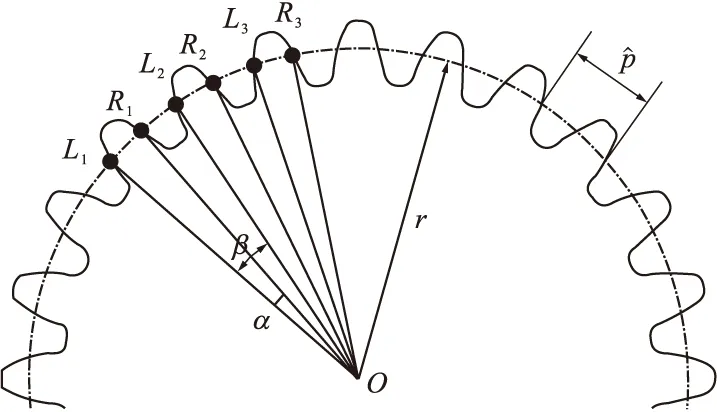
图7 齿距偏差测量

∠LiOLi+1和∠RiORi+1可根据余弦定理求出，有

(8)

实际齿距为

Pi=r×∠LiOLi+1

(9)

理论齿距为

P=πm

(10)

单个齿距偏差为

Δfpi=max|pi-p|

(11)

k个齿距累计偏差为

(12)

齿距累计总偏差为

ΔFp=max(ΔFpk)-min(ΔFpk)

(13)

4.2 齿厚偏差

齿厚偏差测量与齿距偏差类似，理论齿厚为

(14)

实际齿厚为

(15)

齿厚偏差为

ΔEs=s-si

(16)

5 实验及结果分析

利用上述方法对齿轮参数和齿距、齿廓偏差进行测量，测量软件面板如图8所示。圆形标定板重复性精度验证结果如表1所示。

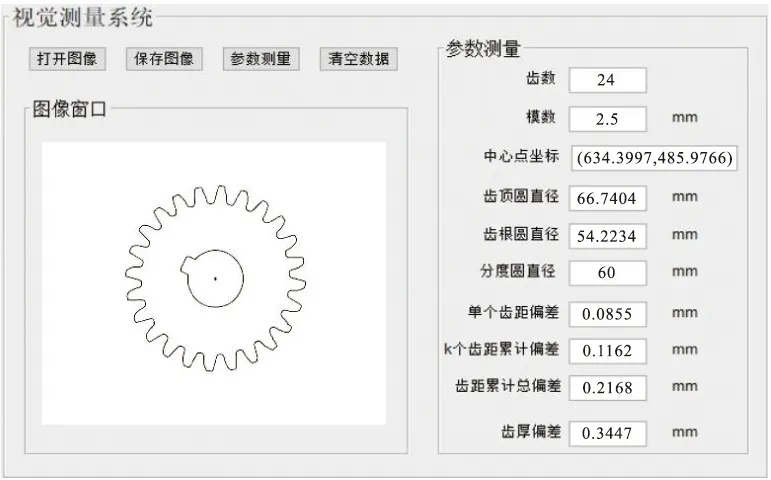
图8 测量软件面板

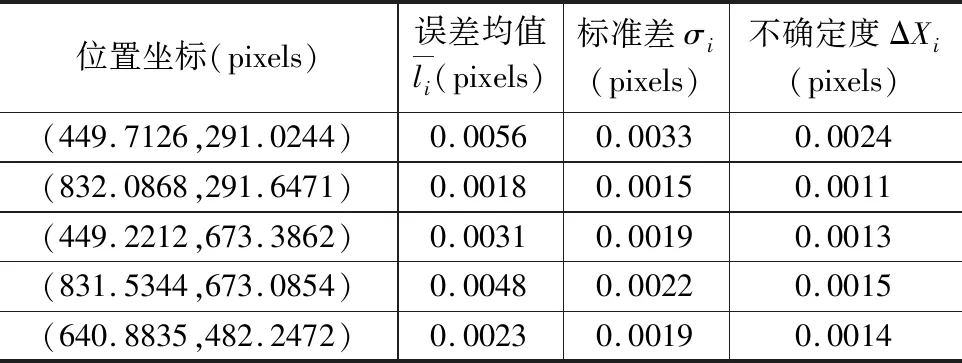
表1 重复性精度测量结果

利用本文测量方法对直齿圆柱齿轮进行测量，将测量结果与人工测量结果进行对比，结果如表2和表3所示。

由表2可知，齿轮、模数和分度圆直径均不存在误差，齿顶、齿根圆直径相对误差均不超过0.2%，满足测量精度要求。

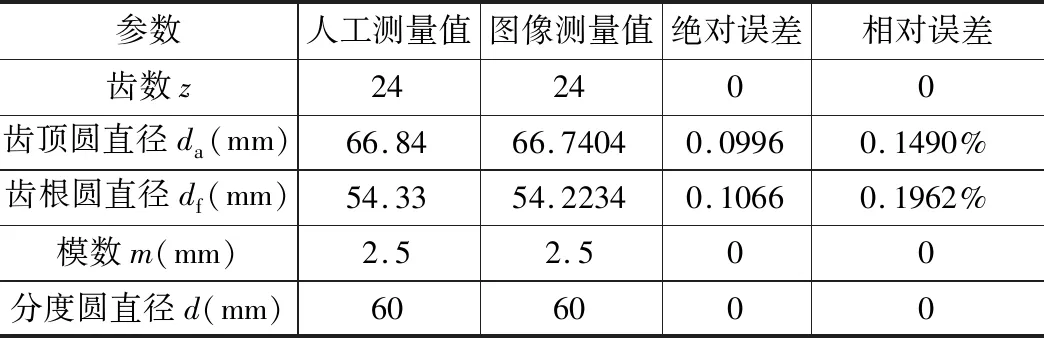
表2 几何参数测量结果对比

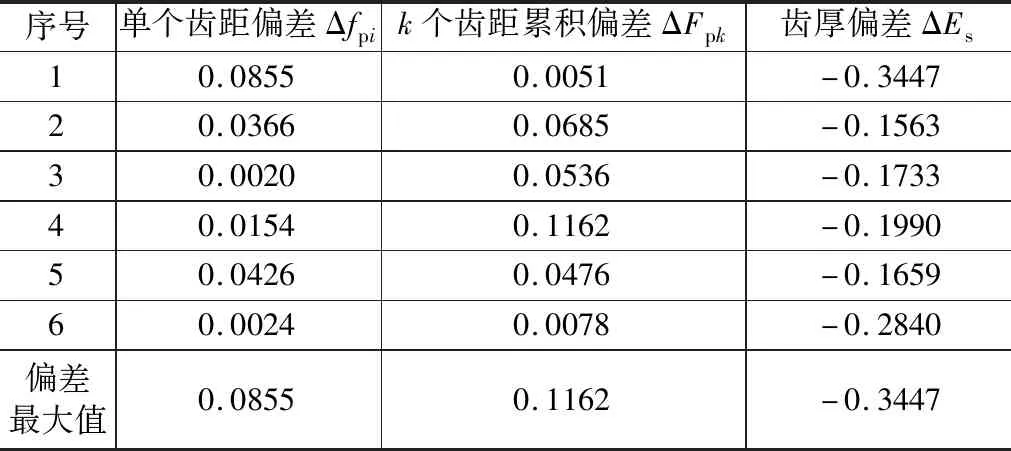
表3 齿距、齿厚误差测量结果对比

表3中，序号表示均匀间隔提取轮齿的测量结果。单个齿距偏差序号1～6表示第1，5，9，13，17，21个齿的齿距偏差测量结果。k个齿距累计偏差序号1～6表示第1，4，7，10，13，16，19个齿间隔k个齿的齿距累计偏差测量结果。齿距累计总偏差ΔFp测量结果为0.2168。齿厚偏差序号1～6表示为第1，5，9，13，17，21个齿的齿厚偏差测量结果。各项偏差结果最大值均在合理范围内，表明测量方法的可行性。