基于Morlet小波和改进峭度的滚动轴承故障诊断方法
2023-01-17田赛姚斌陈彬强王景霖曹新城
田赛,姚斌,陈彬强,王景霖,曹新城
1厦门大学航空航天学院;2故障诊断与健康管理技术航空科技重点实验室
1 引言
数控机床在机械加工中发挥着重要作用,随着运行时长的增加,其各关键部件的磨损易造成精度损失,从而引起加工误差增大,甚至导致部件失效等安全事故。滚动轴承作为数控机床中各部件的关键支撑元件,其工作状态直接决定机床性能、加工精度和可靠性。因此,对滚动轴承的故障特征提取和故障诊断一直是机床故障诊断研究的重点[1]。
王绪虎等[2]基于小波分析,通过去掉滚动轴承故障振动信号高频噪声,在数控机床滚动轴承故障诊断方面取得一定效果。张树等[3]通过细菌觅食算法优化VMD,选取经VMD分解的散布熵最小的模态函数,结合Teager能量谱分析成功应用于数控机床滚动轴承故障诊断。王一鹏等[4]提出基于小波包变换提取轴承振动信号的多个特征向量并作为支持向量机的输入进行故障分类,成功识别出数控机床主轴轴承故障。综上所述,选择有效提取轴承故障信息的特征指标并提高故障信号信噪比是滚动轴承故障诊断的有效手段。
共振解调技术通过带通滤波选取富含轴承故障信息的共振频带来提升故障信号信噪比,对所选频带进行包络解调,根据包络谱中是否有明显的元件故障特征频率来判断故障类型。然而,带通滤波器参数的选择易受先验知识和历史数据的限制[5]。鉴于小波变换良好的局部时频特性,小波分析方法在滚动轴承故障诊断中备受关注[6]。连续小波变换(CWT)和离散小波变换(DWT)作为滤波器均能用于共振解调,但是DWT将频率逐层细分,受频率分辨率的限制易导致最优共振频带的分割。CWT中的Morlet小波时域波形与轴承故障冲击共振响应衰减成分相似,在滚动轴承故障特征提取中得到广泛应用[7]。
包络分析方法中,确定CWT中心频率和带宽参数非常关键。丁康等[8]结合Morlet小波与谱峭度,采用频带平移及外扩的方法定位瞬态冲击激起的共振频带来进行轴承故障诊断。祝小彦等[9]以信息熵指标为评价标准,运用粒子群优化算法优化Morlet小波参数,从而自适应地确定最优共振频带并进行包络解调分析。艾延廷等[10]应用局部包络谱因子指标对中介轴承故障信号进行Morlet复小波共振解调频带优化。然而,峭度指标对偶发性冲击噪声过于敏感,信息熵以及局部包络谱因子指标在强偶发性冲击噪声干扰下仍无法选择合适频带[11]。
综上所述,受外部环境和运行工况的影响,监测信号中可能存在单个强度较大或不同强度的偶发性冲击干扰,针对此问题以及不同强度偶发性冲击噪声干扰下K均值聚类簇数难以预先确定的问题,提出基于Morlet小波和改进峭度的滚动轴承故障诊断方法。该方法采用基于迭代二均值的改进峭度指标,评价小波函数与目标信号的匹配度,通过PSO自适应确定小波最优参数,包络解调分析诊断滚动轴承故障。
2 基于迭代二均值聚类的改进峭度指标
基于四阶矩的峭度指标定义为
(1)
式中,E(·)代表期望运算;μ代表信号X的均值。
采用峭度指标识别故障信号共振频带并结合包络解调分析是滚动轴承故障诊断常用方法之一。然而,当信号只含有单个瞬态冲击时,其峭度值大于包含周期性冲击序列的信号峭度值。针对监测信号中偶发性冲击噪声干扰以及在不同强度偶发性冲击噪声干扰下K均值聚类簇数难以预先确定的问题,提出基于迭代二均值聚类的改进峭度指标,流程如图1所示,描述如下:
(1)将信号X分割为m个等长片段,并计算片段经典峭度Ki{i=1,2,…,m}作为特征值,其峭度最大值Kmax和最小值Kmin为初始聚类中心。
(2)对{Ki}进行迭代K均值聚类分析,识别正常片段。其中,迭代终止条件按以下步骤确定:①输入{Ki},Kmax,Kmin为初始条件({Ki}为初始数据集);②执行聚类簇数为2的K均值聚类,直到类簇中心不变为止,返回分类结果;③通过选择样本数量多的类簇{CKj}剔除含偶发性冲击异常片段;④将{CKj}中峭度最大值CKmax除以最小值CKmin。若CKmax/CKmin小于阈值a,输出{CKj};否则,将CKmax,CKmin,{CKj}返回步骤①更新初始条件。
(3)统计输出结果{CKj}对应正常片段信号的峭度为改进峭度指标。

图1 基于迭代二均值聚类的改进峭度指标
3 Morlet小波最优共振解调
3.1 Morlet小波滤波计算方法
一个能量有限的信号x(t)的CWT可定义为
(2)
式中,WT(a,τ)为小波系数;a为尺度参数;τ为位移参数;*表示共轭函数;ψa,τ(t)为小波基函数。
Morlet小波函数具有指数衰减的震荡形式,与滚动轴承故障产生的瞬态冲击衰减成分类似,常被用于滚动轴承的故障特征提取,其表达式为
(3)
Morlet小波ψ(t)的傅里叶变换Ψ(f)为
(4)
式中,α为包络因子;fc为Morlet小波中心频率。
定义其滤波带宽β为
(5)
根据时域卷积定理,小波滤波过程采用频域相乘,信号x(t)的Morlet小波系数Wx(fc,β)为
Wx(fc,β)=F-1{X(f)Ψ*(f)}
(6)
式中,F-1表示傅里叶逆变换;X(f)是信号x(t)的傅里叶变换。
在应用Morlet小波滤波器提取轴承故障特征时,需要预先设定两个参数,即中心频率fc和带宽β。采用粒子群优化算法(Particle Swarm Optimization,PSO)优化Morlet小波滤波参数[12]。
3.2 Morlet小波最优解调方法
以基于迭代二均值聚类的改进峭度指标评价Morlet小波函数与滚动轴承故障振动信号的匹配度,通过PSO自适应确定轴承故障最优共振频带,包络分析诊断轴承故障,步骤如图2所示。
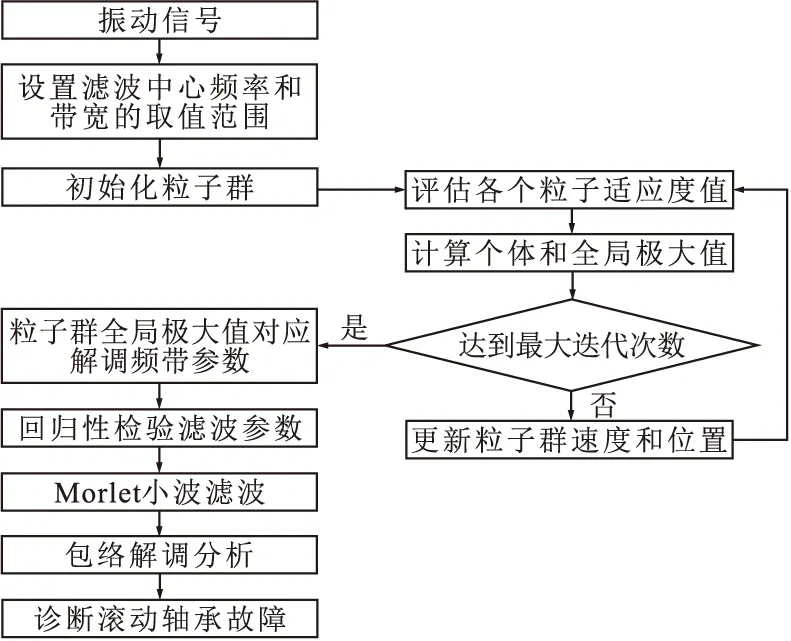
图2 滚动轴承故障诊断流程
故障诊断流程描述如下:①设置Morlet小波滤波中心频率fc和滤波带宽β的取值范围;②初始化粒子群,种群维度为2,数量为30;③计算粒子群的改进峭度指标作为适应度函数,并计算个体极大值和全局极大值;④迭代更新粒子的速度和位置,若达到最大迭代次数,停止迭代,输出粒子群最优适应度值即全局最大值对应共振频带参数,并设置回归性检验保证滤波频带在有效带宽范围内;⑤基于最优共振频带生成Morlet小波滤波器,并对轴承原始振动信号进行滤波;⑥将最佳滤波信号进行包络解调分析,诊断滚动轴承故障。
4 仿真分析
为说明该方法的有效性,采用滚动轴承外圈故障仿真模型进行验证,其表达式为
(7)
式中,仿真信号s(t)包含周期性冲击信号x(t),多重偶发性冲击噪声i(t)以及高斯白噪声n(t)。其中,i(t)参数设置如表1所示,n(t)是均值为0、方差为0.65的高斯白噪声,p(t)为单个偶发性冲击函数;h(t)为轴承故障共振响应函数。
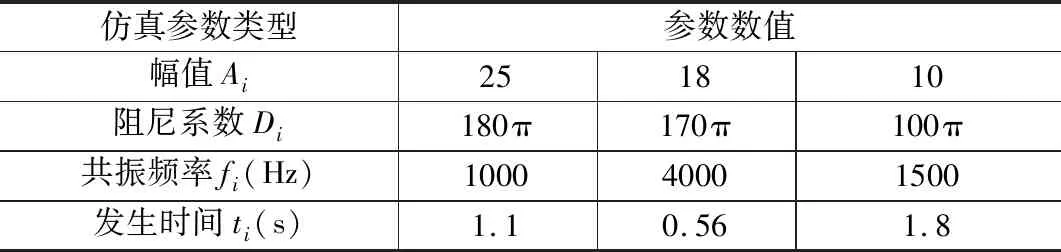
表1 多重偶发性冲击噪声参数
故障特征频率f=30Hz,采样频率Fs=10000Hz,采样长度N=32000,仿真信号如图3所示,明显看出图3a时域波形中存在三个不同强度的偶发性冲击噪声。
分析图3a中的仿真信号,按照图2中的算法流程,设置中心频率fc和带宽参数β的搜索范围分别为[100,4900]Hz,[100,1000]Hz,并设置回归性检验,保证滤波频带在有效带范围内。初始化粒子群,改进峭度指标中阈值a=1.5,分段数m=20,进行50次迭代运算。迭代结果如图4a所示,改进峭度值在第12次迭代运算后收敛于最大值5.04,对应滤波频带参数[2376.5,2593.5]Hz,生成小波滤波器,滤波结果如图4b所示,存在明显的周期性冲击。滤波信号频谱如图4c所示,中心频率与周期性冲击信号x(t)共振频率基本一致,最优共振频带覆盖其共振频率。图4d中,平方包络谱中外圈故障特征频率fo占据主导地位,且高阶倍频明显。分析结果表明,采取本方法能够在强偶发性冲击噪声干扰下提取轴承外圈故障特征。
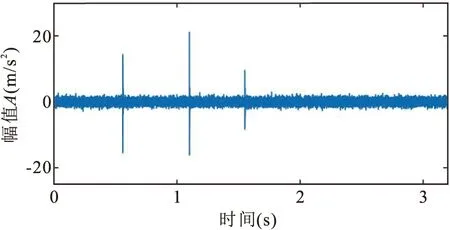
(a)时域波形

(a)迭代过程
作为对比验证,使用峭度指标作为图2算法中适应度函数分析上述仿真信号,分析结果如图5所示。图5a中,峭度值在第15次迭代后逐渐收敛于最大峭度值599,对应滤波频带参数[788,1164]Hz。图5b中,Morlet小波带通滤波时域信号中存在明显偶发性冲击噪声。图5c中滤波信号频谱中心频率与强度最大的偶发性冲击信号p1(t)共振频率f1距离较近,频带宽度覆盖p1(t)的共振频率。图5d滤波信号平方包络谱中未识别到有效故障信息。可知,峭度指标易受偶发性冲击干扰,难以准确识别周期性冲击。

(a)迭代过程
5 实验分析
采用西安交通大学滚动轴承加速寿命实验数据[13]验证提出的方法,实验装置如图6所示。实验选用LDKUER204滚动轴承,转速为2100r/min,施加的径向力为12kN。

图6 滚动轴承加速寿命实验台
采样频率为25.6kHz,采样间隔为1min,每次采样时长为1.28s,采用总样本中某水平方向振动信号。由于本次全寿命滚动轴承实验实际寿命为2h3min,失效位置为外圈,而且在实验结束时该轴承出现外圈裂损,可认为采用的外圈存在磨损,根据滚动轴承几何参数计算外圈故障特征频率为107.91Hz。时域信号如图7a所示,故障信号存在明显偶发性冲击噪声干扰。
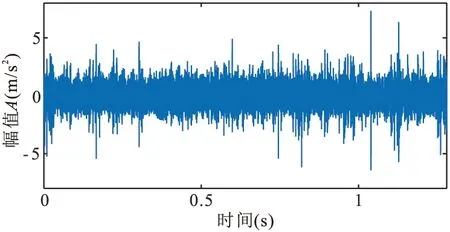
(a)时域波形
按照图2中的算法流程,利用改进峭度指标分析图7a中的实验信号,中心频带、带宽搜索范围分别为[256,12544]Hz、[128,2560]Hz,进行50次迭代,实验结果见图8。
图8a中,改进峭度值在第30次迭代后逐渐收敛于最大值8.8,对应滤波频带为[11339,12605]Hz。图8b中,小波滤波信号时域波形存在重复性瞬态冲击。图8c中,滤波信号频谱显示最优共振频带位于较高频。图8d中,平方包络谱中外圈故障特征频率fo及其倍频2fo明显。因此,本文所述方法可以检测轴承外圈故障。

(a)迭代过程
作为对比验证,按照图2算法流程利用峭度指标分析图7a中的实验信号,结果如图9所示。图9a中,峭度值在第10次迭代后逐渐收敛于最大值17.3,对应最优滤波频带为 [12288,12800]Hz,由于设置回归性检验,最优滤波频带在有效带通滤波范围内。在图9b的滤波信号中可见明显的偶发性冲击,图9c的频谱分析表明滤波信号位于高频,图9d的平方包络谱中难以获取轴承外圈故障特征谱线,未检测出滚动轴承故障。
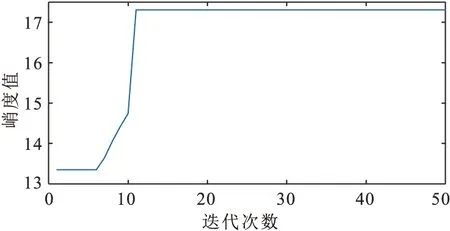
(a)迭代过程
6 结语
针对峭度指标易受偶发性冲击噪声的影响,提出了基于Morlet小波和改进峭度的滚动轴承故障诊断方法。该方法通过基于迭代二均值聚类的改进峭度指标评价Morlet小波和轴承故障信号的匹配度,利用PSO自适应识别出Morlet小波最优参数。仿真和实验结果表明,该方法克服了峭度指标易受偶发性冲击噪声干扰的缺陷,在不同强度偶发性冲击噪声干扰下能够自适应地确定富含故障信息的共振频带,可以进行包络解调分析。
