展现思维过程 促进概念理解
——对“弧度制”教学的思考*
2023-01-16商再金江苏省灌云县教师发展中心222200
商再金 (江苏省灌云县教师发展中心 222200)
翟洪亮 (江苏省太湖高级中学 214125)
1 问题提出
在“弧度制”的一次研讨课中,教师以生活中物理量具有多种度量制为情境,指出角度制的度量值不是十进制的实数,不便于三角函数的运算,需建立一种以十进制实数为度量值的单位制,引导学生回忆初中的弧长公式,获得“用弧长和半径的比值表示圆心角”的认识后,直接指出以弧长等于半径的圆心角为单位建立度量制就能实现简化计算;随即给出1弧度角、弧度制的概念,分析弧度制的本质,建立起角的集合与实数集R之间的一一对应关系,训练两制互化,并介绍弧度制下扇形的面积公式.教学中存在诸多不足,分析如下.
2 问题分析
2.1 创设的情境与弧度制无逻辑关联
教学情境的创设既要符合学生的认知基础,也要体现知识的逻辑关联,便于突破理解障碍.同一个物理量具有多种度量制,虽然符合学生的认知,但与弧度制没有逻辑关联,不能为引入弧度制提供思维指向,也无法为理解弧度制提供认知基础.笔者调查发现,学生对弧度制的理解处在“知其然”的层面,而“不知其所以然”,不理解引入弧度制的根源和1弧度角的“规定”.因此,确定1弧度角的思维过程是教学中必须解决的问题.
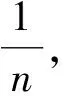
2.2 没有暴露形成单位角的思维过程
弧度制概念的形成需经历两个认知过程:一要实现角的比值表示,即建立弧长与半径的比值与圆心角之间的一一对应关系,这是弧度制的逻辑基础;二要把比值表示转化为度量刻画,这需要确定单位约定的方式.确定度量单位是建立度量制的关键,过程有两类:一类是通过抽象得到的,是思维的结果;另一类是借助工具得到的,是实践的结果,不同的形成过程必然蕴含不同的思维形式[2].授课教师在学生经历第一个认知过程后就直接给出1弧度角的规定,没有揭示规定的缘由,也没有暴露形成单位角的过程,学生只能观察弧度制的外在形式,没有体验到1弧度角的形成过程,弄不清1弧度角与1度角在形成过程中的差异,也就认识不到两者的区别和联系,自然感受不到弧度制蕴含的思想性和创造性.因此,在给出1弧度角的规定之前,应以恰当的问题作为铺垫;在建立1弧度角的概念后,要设置恰当的活动让学生体验1弧度角与1度角在形成方式上的差异,感受弧度制的思想性,认识到两种度量制的区别与联系.
2.3 没有在概念理解中实现创生意义
认知心理学认为,理解一个主题要建立与之有关的心智模式或图式,要求学习者运用已有知识在新的信息中创生意义、在事实与观点间建立联系.这样才能使知识成为数学发展中的结点,才是具有活性的可应用的知识.两种度量制的互化是显性的、自然的,不会导致理解障碍,互化技能的训练也是必要的.但还应设置促进概念理解的教学活动,促使学生运用弧度制的知识构建网络、实现具有创生意义的学习,并认识到引入弧度制的必要性、合理性和优越性.
3 问题解决
3.1 明确差异,在统一度量中引入弧度制
在初中,三角函数的自变量是角度,这与幂、指数、对数等初等函数的自变量为实数是不同的,启发学生思考如何解决两者的差异.引导学生回顾角度制,指出由于地域或功能的差异导致等分圆周的数目不同,如用于天文学的12等分、中亚两河流域的360等分、欧洲的400等分和军事上的6 000等分.目的是让学生看到建立角度制的动力源自数学外部的实际需求,意识到等分圆周时具有一定的偶然性和随意性.随着数学的发展,三角学的重点从强调计算变成强调函数方法,角与长度的单位制不统一带来诸多不便,建立统一的度量制是数学自身发展的必然,而初等函数中自变量的单位为实数1,从而想到能否统一用单位长度去度量角.
圆的两要素为圆心和半径,故只能用半径去度量角.而同圆中两条长度不同的弦的长度之比不等于其对应角度之比,故只能用半径去度量角所对的弧,这样引入弧度制就显得自然.如图1,“自变量的单位为实数1”是促使用半径去度量弧长的出发点,也是弧度制教学的切入点,更是优化弧度制计算促使单位圆产生的导火索,还为三角函数的概念、诱导公式学习奠定基础,体现数学知识之间的连贯性与整体性,规避了碎片化教学,促进知识体系的构建.
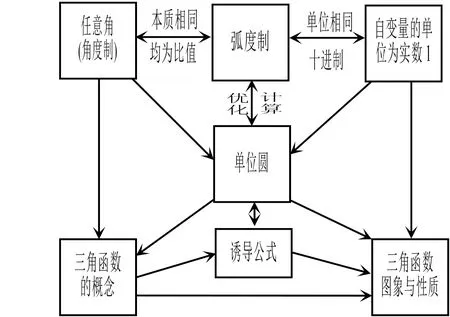
图1
3.2 仿圆周率,通过类比实现概念再创造
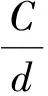
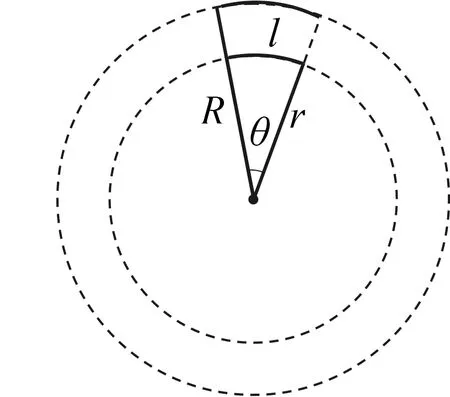
图2
3.3 建立具象,在冲突中促进概念的理解
弧度制单位角是人类抽象思维的结晶,具有较高的抽象性,需要直观的具象来促进理解.笔者的做法是在引出两种度量制的换算关系前,指示学生先画出弦长等于半径的圆心角,让他们先获得1 rad角比60°角略小的感性认知,再用弧度制视角研究整个圆周角,易得圆周角360°=2π rad,从而进行角度制与弧度制之间的互化,获得1 rad精确的角度数,建立1 rad的图形.目的是把建立具象的过程转变成促进概念理解的过程,完善学生的认知结构.
3.4 借助图形,发现不等式中的创生意义
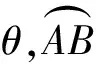
图3
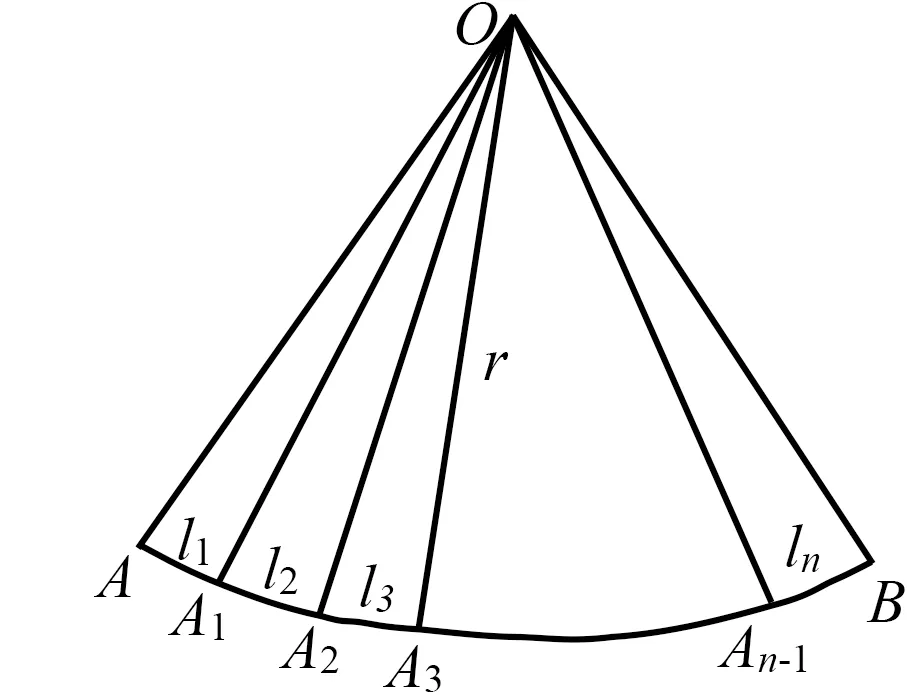
图4
4 教学反思
4.1 要注重弧度制概念的生成过程
弧度制教学要注重概念的生成过程.许多教师在概念教学中,往往不注重概念的形成过程,仅注重概念的运用,出现“斩头去尾烧中段”现象,忽视学生的主体地位,阻碍了学生思维能力的发展.弧度制概念教学应注意引入背景的选择,认清根源是由于数学自身发展的需要,实现从几何到代数的跨越是统一度量的必然,然后从确定圆的要素中寻找切入点,联想圆周率,通过整体与部分进行类比,还原出知识产生、发展的原貌,引导学生对1弧度角的“再创造”,激发兴趣,启迪思维,把数学“冰冷的美丽”转化为学生“火热的思考”,展现思维过程,促进概念内化,构建知识体系,发展学生能力,提升学生素养.
4.2 要适度运用措施防止误导学生
弧度制教学要注意强化措施运用的适度性.弧度制与角度制除了“单位”不同外,“没有本质上的差别,而且还关系密切”[3],它们没有优劣之分,只是角度制更适用于几何的方法,而弧度制更适用于代数的方法.但是,弧度制单位角创立形式的抽象性、省略弧度制单位的记法、角的比值表示等客观因素容易放大弧度制的特殊性.教学中的一些强化措施,如过分强调角的比值表示,无形中传递出“约去单位”的信息;过分强调弧度制度量值集合与实数集R之间的一一对应关系,会带来“角度制不能建立一一对应关系”的负迁移.因此,在促进学生深化理解的同时,不掩盖共性也不放大差异,不能贬此褒彼.
4.3 要充分发挥数学学科育人功能
弧度制的教学是体验创造和感悟数学理性的载体,也是培育科学创造观的良好契机.弧度制的创立是数学发展的历史必然,弧度制萌芽于古希腊时代,但直到18世纪才成为度量单位制,由于这期间三角函数主要是运用于天文学、圆或解三角形的工具,而角度制恰好适合几何研究.到了近代,微积分的迅猛发展使数学研究转向到代数分析,三角函数成为刻画周期现象的模型,需要更高层次的抽象概括,从数学内部抽象而来的弧度制也就应运而生,从这个意义上讲,弧度制的建立是纵向数学化的结果,而角度制则是水平数学化的结果.因此,弧度制的概念教学既要展示数学思维的力量和数学的理性光芒,也要揭示数学发展的背景趋势和知识的生成过程,培育学生科学的创造观,发挥数学学科的育人功能.
