1种管壳式冷凝器优化设计新方法

崔祎，常承林，王彧斐

（1.中国石油大学（北京）自动化系，北京 102249；2.重庆大学化学化工学院，重庆 400044）

冷凝器的种类繁多，按接触方式不同，可分为蓄热式、混合式及间壁式等[1-3]；按传热面形式不同，可分为管壳式、板式及翅片式等[4-5]。其中，管壳式冷凝器以其易生产、低成本、清洗方便和处理量大等优点，成为化学工业中应用最广泛的冷凝设备[6]。

王开锋提出了1 种基于遗传-模拟退火算法对管壳式冷凝器的详细设计，分析了了有相变情况下，管内外径、管长，挡板数量和管程数等设计变量对于冷凝器费用的影响，对换热面积与压降进行全面的权衡[7]；彭岚建立了数值计算模型，采用遗传算法，研究管外径、管间距、管壁厚等变量对于冷凝器重量的影响[8]；刘成洋等采用改进的遗传算法，研究了管外径和管间距对于冷凝器重量和体积的影响，该算法的精确性和收敛性都得到了充分的验证[9]。

HASSAN 等以管程数、管束布局等为设计变量，以冷凝器总成本为目标函数，对比遗传算法和粒子群算法的优劣，发现遗传算法的收敛速度更快[10]；ALLEN 等，以管间距、挡板间距、壳程直径和管外径等为设计变量，建立了冷凝器费用的优化模型[11]；PATEL等采用粒子群优化，考虑管内外径、挡板间距和管束布局等设计变量，对冷凝器年度总费用进行优化，其结果显示，粒子群优化具有较高的准确性和收敛性[12]；NASR等开发了1 种新型蒸发式冷凝器设计方法，提供换热面积、压降以及传热传质系数之间的关系，在最大允许压降条件下，计算得到最小换热面积，减少了试算次数[13]。

基于Kern 方法，GONÇALVES 等采用混合整数非线性优化来最小化换热面积，发现大多数情况下模型不收敛[14]。设计变量均为离散值，他们将混合整数非线性模型转化为混合整数线性模型，实现了全局求解。此外，GONÇALVES 等根据换热器机械部件的标准值，定义了多个二进制变量来组合离散的设计变量，加快了混合整数线性模型的求解[15]；GONÇALVES等又基于Bell-Delaware方法建立混合整数线性模型，实现了年度总费用的最小化优化[16]。LEMOS 等开发了集合修建算法，利用不等式约束顺序消除不可行得到换热器设计变量，以最小化换热面积为目标，经过算例测试表明，该方法大幅提高了计算效率[17]。PEREIRA 等将冷凝器的混合整数非线性规划转换成为整数线性模型，采用整数线性求解，该模型不需要初始值，同时避免了局部优化解[18]。

在以上研究中，现有的算法能够在一定程度上解决冷凝器的设计问题，但是他们都不能完全保证得到解的全局优化性，虽然采用随机优化方法或添加随机算子可以避免陷入局部最优，但需要多次尝试才能实现，结果也需要进一步验证。此外，很多文献中的方法依赖于人工提供初值，对参数进行多次调整，这使得很多算例的求解过程及结果无法重现。同时，初值的选择会极大地影响算法的求解速度，无法保证算法的收敛性能。

针对上述问题，笔者首先介绍了冷凝器详细设计的数学模型，包括热力学和水力学方程，以及最小化换热面积和冷凝器功耗的目标函数等。采用文献[18]中算例，以面积最小化为目标进行优化计算，将计算结果与文献比较分析，然后以最小化冷凝器功耗为目标进行计算，求出不同换热面积条件下的最小冷凝器功耗，进行功耗与换热面积间的权衡。另外，还进行了冷凝器功耗与换热面积的权衡，给出在冷凝器操作费用方面表现更优的设计方案。

1 数学模型

根据冷凝器布置的空间方向（水平或垂直），管壳程中冷热物流分配，管壳式冷凝器主要有4种类型，即壳程冷凝的卧式换热器、管程冷凝的卧式换热器、壳程冷凝的立式换热器和壳程冷凝的立式换热器。以壳程冷凝的卧式换热器为例，开发冷凝器详细设计的新方法。

研究基于以下几点假设：1）冷凝器壳程为E型；2）壳程物流冷凝只发生相变，进出口前后温度保持不变；3）管程冷却剂为湍流，且不发生相变；4）物性参数恒定，取平均温度下的数值。

在优化模型的描述中，初始给定、无需优化的参数，其顶部带有符号“ˆ”。

1.1 符号含义

1）参数。Âexc，面积裕量；Ĉ，相关参数；ĉpt，管程物流比热容；ĝ，重力加速度；ks，壳程导热系数；kt，管程导热系数；ktube，管壁导热系数；ms，壳程质量流量；Q，热负荷；mt，管程质量流量；Prt，管程普朗特数；Rfs，壳程热绝缘系数；Rft，管程热绝缘系数；Tcl，冷物流入口摄氏温度；Tco，冷物流出口摄氏温度；Thl，热物流入口摄氏温度；Tho，热物流出口摄氏温度；vsmax，壳程最大流速；vsmin，壳程最小流速；vtmax，管程最大流速；vtmin，管程最小流速；Hvap，汽化质量焓；Δpsdisp，壳程允许压降；Δptdisp，管程允许压降；ΔTlm，对数平均温差；μs，壳程冷凝水黏度；μt，管程冷凝水黏度；μvs，壳程蒸汽黏度；ρs，壳程冷凝水密度；ρt，管程物流密度；ρvs，壳程蒸汽密度；ϕv0，平均两相压降系数；η，电机效率。

2）变量。A，实际换热面积；Ar，壳程流动面积；Areq，所需换热面积；Deq，等效直径；Ds，壳程直径；dte，管外径；dti，管内径；FAR，自由面积比；Fs，壳程摩擦系数；Ft，管程摩擦系数；FSC，冷凝器结构系数；FTC，管束修正系数；hs，壳程传热系数；ht，管程传热系数；K，压降参数；Klay，管束布局参数；L，管长；lbc，挡板间距；ltp，管间距；Nb，挡板数量；Npt，管程数；Ntp，每次物流流动通过的管数；Ntt，总管数；Nut，传热单元数；Res，壳程雷诺数；Ret，管程雷诺数；U，总传热数；vs，壳程流速；vt，管程流速；W，冷凝器功耗；Δps，壳程压降；Δpsv0，入口条件相关的壳程压降；Δpt，壳程压降；rp，间径比。

1.2 冷凝器数学模型

1.2.1 管程热力学方程及水力学方程

湍流时，管程的热力学方程为：

式中，管束布局参数Klay，三角形、正方形布局时分别取0.866、1.0。FTC取值见表1。

表1 管束修正系数取值Tab 1 Tube bundle correction factor value

FSC与冷凝器头型相关，当＞0.337 m时，其取值见表2。

表2 结构参数取值Tab 2 Structure factor value

管程的水力学方程为（忽略了接管处的压降）：

式中，压降参数K，单管程时取0.9，双管程或多管程时取1.6。

管程摩擦系数的计算：

1.2.3 总传热系数方程

1.2.6 冷凝器功耗方程

冷凝器功耗的计算：

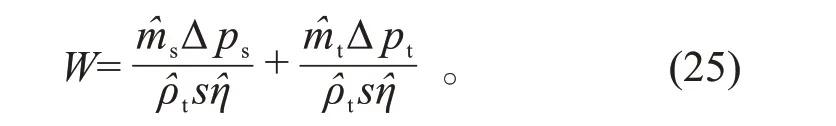
式中，电机效率η取75%。

1.3 约束条件

为保证模型中方程的有效性以及冷凝器的正常工作，该模型的约束有热力学、水力学约束，流速约束以及结构约束。

1.3.1 热力学、水力学约束

管程和壳程的压降需在允许范围内：

对流速也做一定的限制：

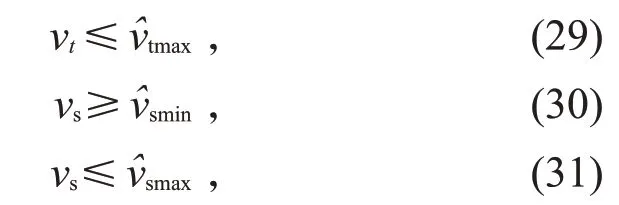
为保证壳程和管程方程的有效性，对雷诺数也做出限制：

为保证生产安全以及冷凝器的正常运行，实际生产中一般都会设定裕量，使冷凝器有额外的换热面积，实际换热面积应满足条件：

1.3.2 冷凝器结构约束

挡板间距与壳程直径约束为：

1.4 目标函数

目标函数为：1）MinA；2）MinW。

2 案例研究

2.1 案例介绍

研究的算例程序均在GAMS 24.2.3中运行。对于设计变量为离散变量的算例，可以采用枚举法进行求解。其方法原理为：先计算出所有可能的目标函数值，然后再设置相关的约束条件，求出符合条件的目标函数值，进而给出相关的设计变量。此方法的求解空间为全局，因此保证了解的全局最优性；同时，枚举法要计算出所有的目标函数可能值，所有不需要给定初始值。

理论上所有设计变量为离散变量的算例均可采用枚举法，但因为枚举法要计算出所有可能的目标函数值，所以对于设计变量过多的算例，其计算耗时较长。

该算例是1个用于冷凝纯丙酮的蒸馏塔顶冷凝器，由SMITH等提出，PEREIRA等对其进一步求解[18,20]。为保证换热面积与PEREIRA等的结果等效比较，本案例优化时，不考虑额外的面积裕量，即Âexc=0，同时管壁厚取2 mm，管壁的导热系数ktub取45 W/(m·K)。

表3给出设计变量的集合，这些离散值符合商业标准。表4给出冷热物流的物性参数（其中流速范围及允许压降由PEREIRA等给出）。数值在模拟过程中保持不变，取平均温度下的值。

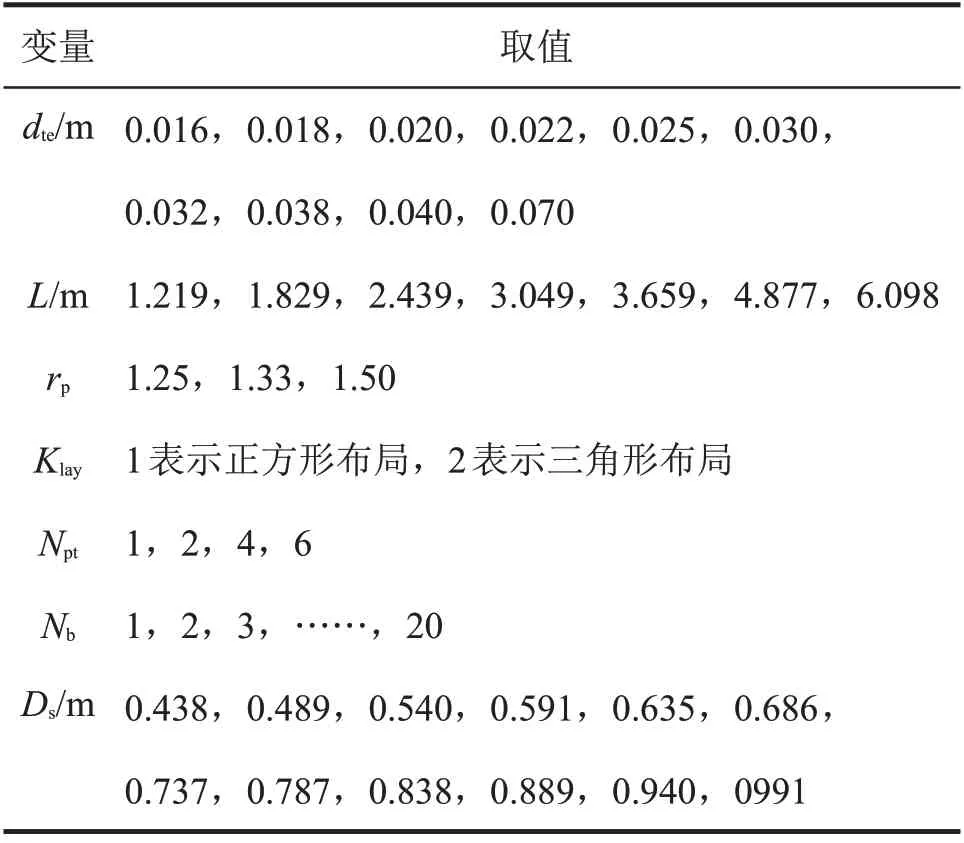
表3 设计变量的集合Tab 3 Collection of design variables

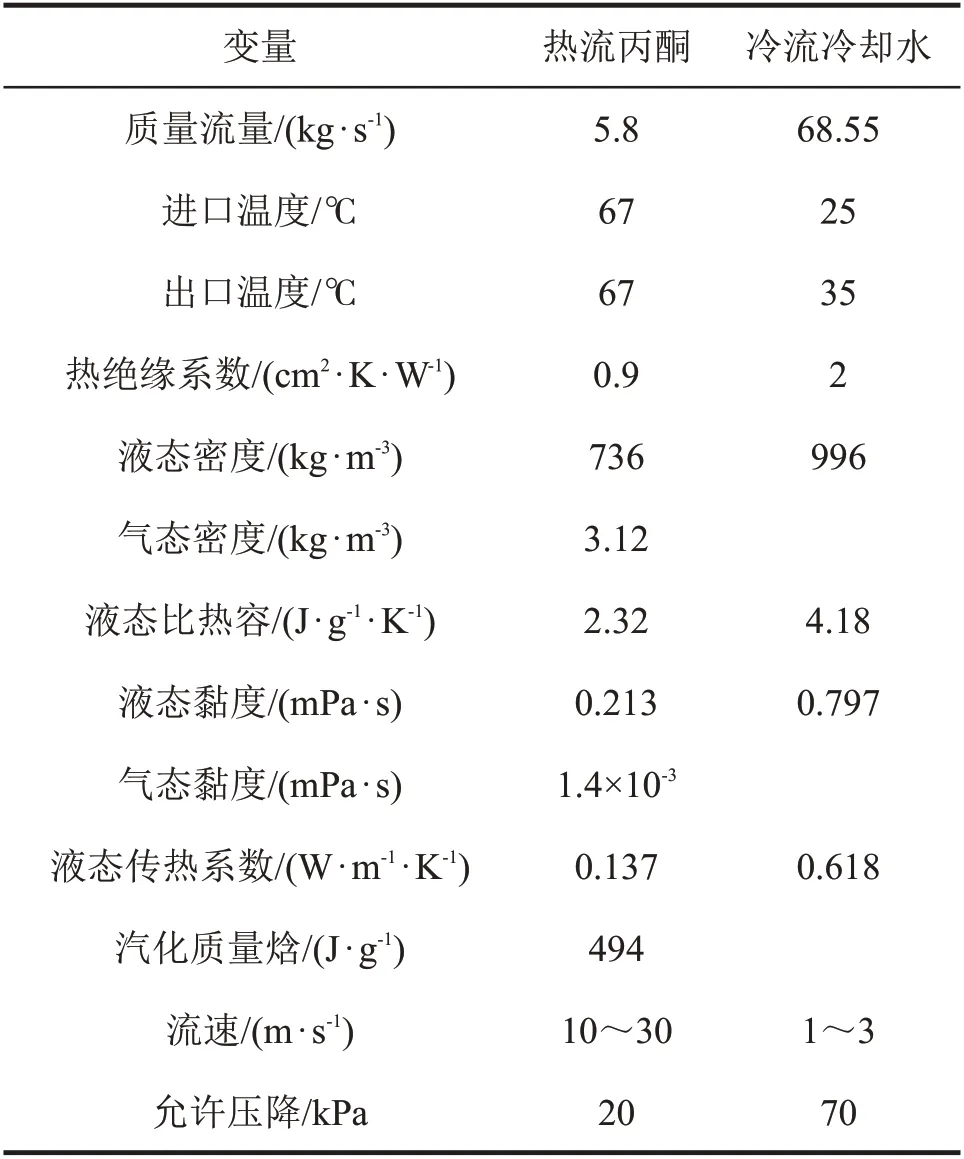
表4 物流数据及物性Tab 4 Stream data and physical properties

2.2 最小化换热面积

根据表4，以最小化换热面积为目标优化，所得的结果见表5。

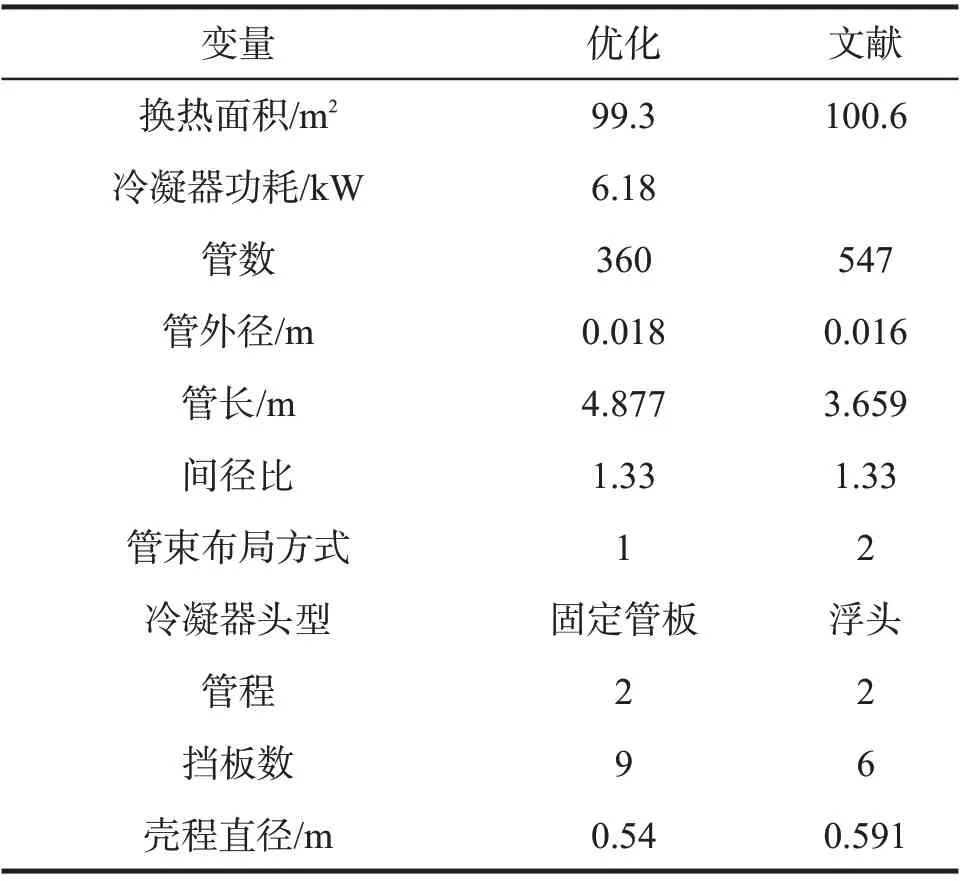
表5 换热面积优化结果Tab 5 Optimization results of heat exchange area

采用枚举法，因为要计算出所有可能的目标函数值，故与采用求解器的PEREIRA 等相比，其计算过程较慢。

所采用的优化方法得到了比文献更小的换热面积，为99.3 m2，但与文献相差不大，仅减小了1.29%，原因是在优化过程中考虑了冷凝器头型变量，而文献在优化前就指定冷凝器头型为浮头式。优化结果选用的冷凝器头型为固定管板式，针对该算例而言，物流温度压力并不是高温高压，采用固定管板的冷凝器头型满足生产需求的同时费用较低，明显更加符合生产实际。

在管数方面，得到的优化解为360，与文献相差较大，减少了34.17%。所得到的管束布局方式为正方形布局，虽然正方形布局在同等换热面积下的布管数少于三角形布局，但在能满足生产需要的条件下，采用正方形布局以及更低的管数，降低了布管的难度，降低了冷凝器的体积与重量，减少冷凝器的费用，更符合实际生产需求。

优化所得的管程压降为65.28 kPa，壳程压降为18.20 kPa，与文献的48.93 kPa和16.73 kPa相比较高。因为优化结果选取的挡板数量为9，相比文献偏大，故导致得到的壳程流速为28.4 m/s，比文献的24.3 m/s更高，壳程流速较大使壳程压降高于文献。而管程压降较高则是因为优化取的管外径和管长比文献大，导致了管程物流流速2.5 m/s 比文献的2.2 m/s 较高，提升了管程压降。虽然优化结果的管程、壳程压降均比文献大，但也仍在允许压降范围内。

优化所得的管、壳程传热系数分为10.67、1.331 kW/(m2·K)，总传热系数为0.788 0 kW/(m2·K)，与文献相差不大，这也使优化换热面积只是略小于文献的原因。

2.3 功耗与换热面积的权衡

在该算例的优化中存在冷凝器头型的选择，不同冷凝器头型的费用相差较大，以冷凝器总费用为目标进行优化可能会导致冷凝器头型在优化中比例过大，因此为了尽可能体现所有设计变量对于冷凝器设计的影响，在设计约束条件下，增加换热面积的限制，选择以最小化冷凝器功耗为目标进行优化，求出不同换热面积条件下的最小冷凝器功耗。不同换热面积下最小冷凝器功耗见图1。

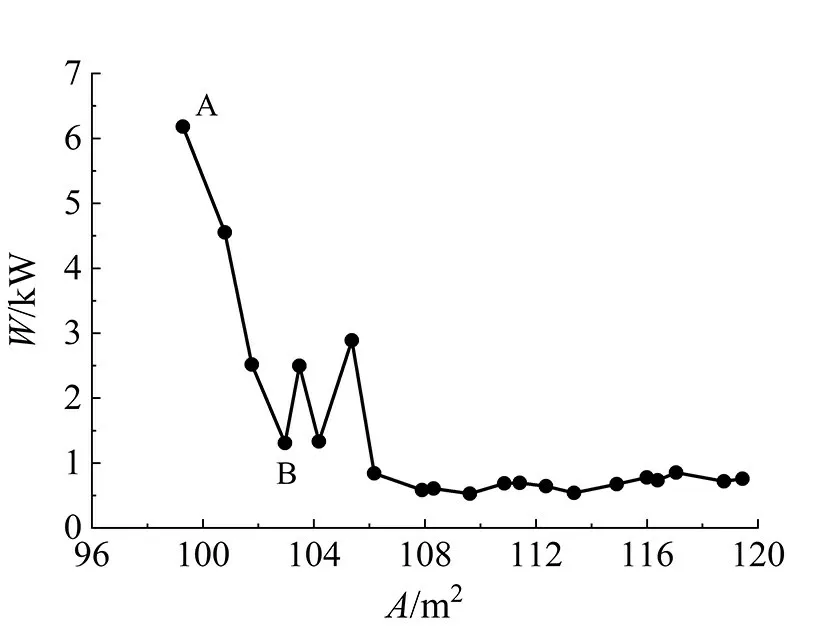
图1 不同换热面积下的最小功耗Fig 1 Minimum power consumption under different heat exchange areas

从图1可以看出，功耗随着换热面积的增加不断下降。在100～105 m2内波动下降，在105 m2之后逐渐趋于恒定。该算例中的管程流量及压降均远大于壳程，而压降又由流速控制，根据式(25)可知，在冷凝器功耗计算中，功耗主要是由管程流速控制。当换热面积限制在100～105 m2时，距离优化结果给出的最小换热面积较近，此时最小化冷凝器功耗，满足设计约束与换热面积限制的解较少，在满足限制的条件下，管程流速距离vtmin较远，导致此阶段管程流速较高且波动明显，所以图1中冷凝器功耗呈现大幅度的不规则波动。当换热面积取大于105 m2后，满足设计约束与换热面积限制的解增加，此时最小化冷凝器功耗，管程流速普遍会更加接近vtmin，进而使冷凝器功耗降低且趋于稳定。

图1中A点为最小化换热面积所得数据点，即优化结果数据点，可见最小化换热面积所得结果对应的冷凝器功耗最大，因此考虑到冷凝器操作费用等实际问题时，有必要将面积和功耗等因素同步考虑。

基于上述分析，选取B点情况下的设计变量作为权衡后的结果，给出冷凝器功耗与换热面积进行权衡后的设计方案，见表6。

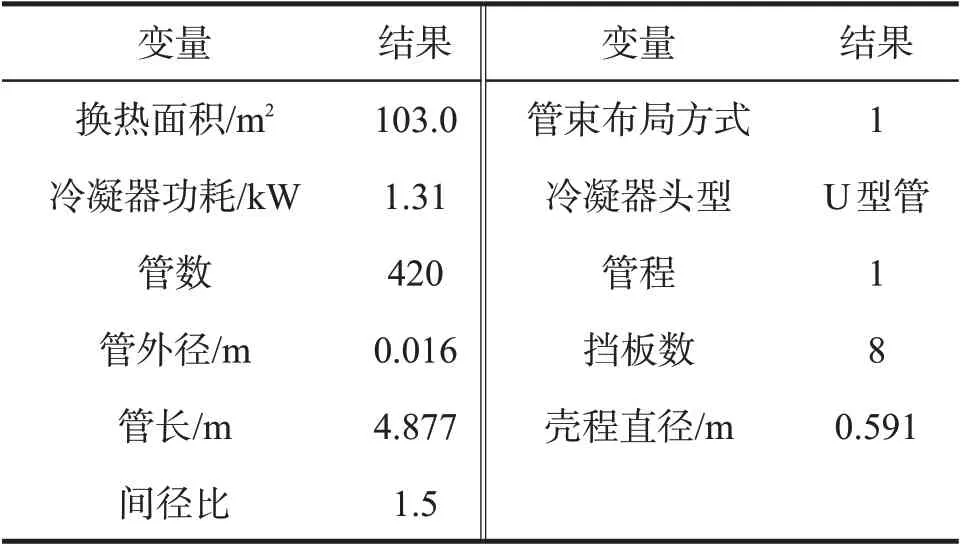
表6 权衡结果Tab 6 Compromise result

由表6可以看出，在此设计方案条件下，对比最小换热面积条件下的功耗6.18 kW，冷凝器功耗降低了78.80%，而换热面积仅增加了3.73%，综合考虑权衡方案在冷凝器操作费用方面表现应优于最小换热面积方案。

3 结 论

与文献[18]相比，采用枚举法的优化方法，无需设定初始值，还可以保证解的全局优化性；同时优化过程中还考虑了冷凝器头型对于换热面积的影响，给出了更加符合实际的最小换热面积设计方案。

笔者提出的1种管壳式冷凝器详细设计的新方法。该方法不依赖于商业求解器，无需设定初始值，且能保证设计解的全局最优性。

以最小化换热面积为求解目标，得到结果与文献对比发现，头型的选择对冷凝器换热面积影响并不明显，但可能影响到冷凝器的管束排布方式，同时考虑到冷凝器头型的优缺点及物流属性，头型选择对优化结果仍有重要的影响。

还以最小化冷凝器功耗为目标进行优化，得到不同换热面积条件下的最小冷凝器功耗，进行功耗与换热面积间的权衡，最终给出了权衡后的设计方案。权衡后的设计方案条件下，冷凝器功耗为1.31 kW，比最小换热面积条件下的功耗降低了78.80%，而换热面积仅增加了3.73%。