地磁测量卫星的矢量磁场在轨标定算法仿真*
2023-01-14杜雯黄河周军
杜雯 黄河 周军
(西北工业大学航天学院 西安 710072)
0 引言
地磁测量卫星是获取高精确地球磁场数据的重要手段,可为资源勘探、磁场导航、空间环境监测等领域提供技术支撑[1,2],例如丹麦Oersted 卫星、德国CHAMP 卫星、欧空局Swarm 星座任务以及中国张衡一号电磁监测试验卫星等。中国目前正在开展高精度磁场测量卫星的研制,然而对于高精度磁场测量卫星的数据标定问题,特别是从0 级到1 级数据的处理,还缺少系统研究[3]。
高精度地磁测量卫星的地磁场测量载荷主要包括矢量磁强计、标量磁强计和星敏感器。其中,矢量磁强计探测三分量矢量磁场,标量磁强计探测地磁场强度。通常为了避免卫星本体磁场干扰对磁强计测量的影响,将磁强计安装在星体外伸展杆的光学平台上。由于工艺水平的限制,矢量磁强计在实际使用过程中受到三轴非正交角、标度因子以及偏差的影响,其测量值不能作为绝对准确值。在卫星发射前,矢量磁强计会在实验室进行校正和对准(飞行前校正)[4]。由于卫星在轨运行的环境条件实验室无法真实模拟,同时矢量磁强计的偏差和标度因子受时间和温度的影响,矢量磁强计数据的定期校准是保证精确测量的必然选择[5]。
地球磁测卫星磁场数据校正精度要求高,校正过程需考虑测量仪器参数的变化以及矢量磁强计所处平台的条件,保证校正后的磁场误差在满足精度要求的前提下尽可能节省运算时间。
对于卫星地磁场数据校正问题,主要有两种思路:一是采用基于椭球轨迹约束的误差修正方法,即针对固定点的磁场测量值约束在椭球轨迹上[6-7],该方法限制磁场强度为定值,不符合地磁测量卫星大范围磁场测量的要求;二是卫星在轨工作过程中,对磁强计进行标定,其基本思想是基于大量在轨实测磁场强度数据和磁场三分量矢量数据,由两种数据获取磁场强度的标量差值,进而辨识磁强计误差参数,保证在仪器参数变化情况下仍能获取高精度磁场数据。对于矢量磁强计的标定问题,文献[8,9]利用CryoSat-2卫星在轨数据,探讨了星体内平台磁强计测量数据的预处理和校准步骤,并考虑了蓄电池、太阳能电池以及磁力矩器引起的磁干扰;文献[10]结合已校准的磁场数据和地磁台数据对多个卫星平台磁强计的参数和磁场参数进行联合估计,建立了时变地磁场模型;文献[11]针对高精度星敏感器受温度影响带来的误差进行研究,采用欧拉角与平台不同位置温度的线性关系进行建模分析,改善了姿态确定精度,得出星敏感器坐标系与地磁参考系之间的误差角并非完全由光行差引起,同时受平台温度分布影响的结论。文献[12] 研究了在CHAMP 卫星与SWARM 卫星数据空缺的情况下,采用线性化方法对卫星平台式磁强计数据进行校准整理,弥补了数据空缺;文献[13]采用改进的最小二乘算法,对磁通门磁强计三轴正交性和零点漂移进行修正,但其校正模型需进行多项式代入合并,过程较为繁复。对于矢量磁强计多参数估计的情况,计算过程更加复杂。
本文针对地磁测量卫星数据精度要求高、外部环境条件不确定等特点,考虑矢量磁强计非正交角、标度因子和偏差的影响,建立矢量磁强计9 参数线性误差模型,利用标量磁强计的磁场强度数据,分别设计了基于小量近似的线性校正算法和基于参数辨识更新的非线性校正算法并进行仿真校验,实现对矢量磁强计参数的辨识分析,考虑了测量噪声对校正算法精度的影响。同时,为避免标量测量值中的异常值对算法精度的影响,将算法中的权重函数改进为Tukey 权重函数。结果表明,在矢量磁强计9 参数误差模型及特定的噪声状态下,线性算法与非线性算法校正结果相似,误差均在0.5 nT 以内,满足高精度磁场数据探测的需求,适用于地磁测量卫星的0 级数据校正。
1 矢量磁强计线性输出模型
地磁测量卫星为保证地磁场测量的精确性,配备有多种磁场测量载荷,包括VFM 矢量磁强计、ASM标量磁强计以及高精度星敏感器。在卫星进行磁场数据处理之前,应已根据GNSS 载荷观测得到精密轨道数据;矢量磁强计测量其坐标系下磁场三分量值,标量磁强计测量地磁场总强度,校准磁场矢量测量结果;去除卫星本体的磁场扰动,对磁场数据进行重采样,结合惯性姿态信息将磁强计输出磁场转换至地理坐标系下。所有处理部分均依赖于发射前在地面对载荷与卫星进行的标定与测试,其标定测试的参数结果准确性决定了星上数据处理的精度。为获取矢量磁强计的精确指向信息,同时保证磁场测量精度,矢量磁强计与星敏感器安装在星体外伸展杆中部的光学平台上[14]。高精度星敏感器包含三个观测单元,测量矢量磁强计的惯性姿态信息(孔间角误差<3'')。该安装结构在Oersted,CHAMP 和SWARM 卫星上都有所应用。此结构既减小了矢量磁强计内部线圈对标量磁强计磁场测量的影响,还可以确保磁强计输出结果中来自卫星本体磁场的磁净度。本文重点研究矢量磁强计输出数据在非正交角、标度因子以及偏差的影响下,利用标量磁强计读数对磁场矢量进行标量校正的数据处理方法。
矢量磁强计线性输出模型如下[15]:

式中,BVFM=[Bx,By,Bz]T(单位nT)为矢量磁强计处的真实磁场矢量,E=[Ex Ey Ez]T(单位nT)为矢量磁强计输出磁场矢量,矩阵S∈R3×3为矢量磁强计的标度因子矩阵,矩阵P∈R3×3描述正交系下真实磁场矢量转换至矢量磁强计的非正交系下,b=[bx0by0bzo]T(单位nT)描述矢量磁强计三轴固有偏差。
矢量磁强计的标度因子矩阵S为三轴灵敏度构成的对角阵形式,不考虑轴间干扰,可写为
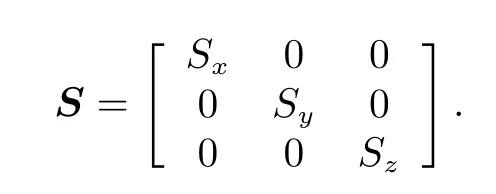
式中,Sx,Sy,Sz分别为三轴标度因子,三者均为接近1 的常数(无量纲),不考虑轴间串扰。
考虑到矢量磁强计机械轴不可能完全正交,三轴非正交角定义如图1 所示。Ox′y′z′表示矢量磁强计测量磁场非正交坐标系,Oxyz为正交坐标系,U1,U2,U3表示正交系与非正交系之间的夹角,三者均为小角度。非正交系坐标轴x′轴投影在Oxy,Oxz平面,与x轴的夹角分别为非正交角U2,U3;y′轴与y轴的夹角为非正交角U1;z′轴与正交系z轴重合。
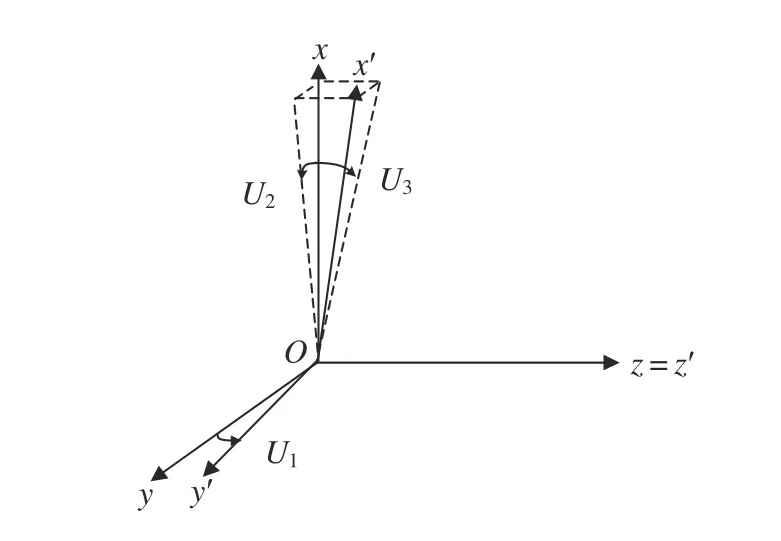
图1 非正交角定义Fig.1 Definition of the non-orthogonalities
描述矢量磁强计非正交性的矩阵可表示为

2 标量校正算法设计
针对以SWARM 为代表的地磁测量卫星矢量磁强计与标量磁强计的安装特点以及工作原理进行校正算法设计。
标量磁强计利用塞曼效应进行磁场测量,其测量值与磁场方向、温度和时间无关。而且,由于标量磁强计距离卫星本体较远且不受外界环境影响,可利用磁场标量测量值对矢量数据进行校正。
2.1 基于小量近似的线性校正算法
在矢量磁强计线性输出模型基础上,由于U1,U2,U3均为小角度,式(3)可简化为[16]

式中,ax′y′,ax′z′,ay′z′表示传感器任意两轴间夹角。式(4)可记为

式中,k1~k6为线性校正模型的校正系数。
矢量磁强计处的地磁场强度为
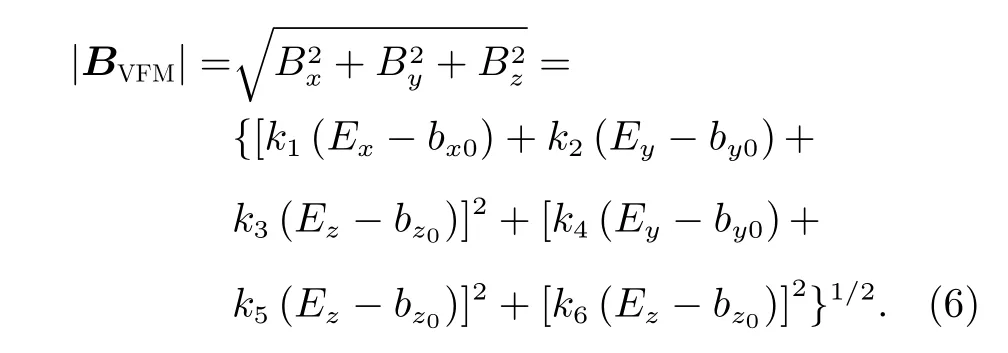
矢量磁强计三轴输出值为
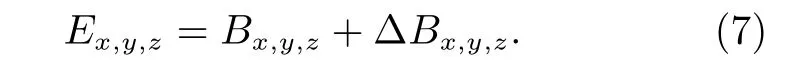
式中,ΔBx,y,z为矢量磁强计测量误差。由式(5)可进一步得到

矢量磁强计与标量磁强计磁场测量的标量残差可表示为
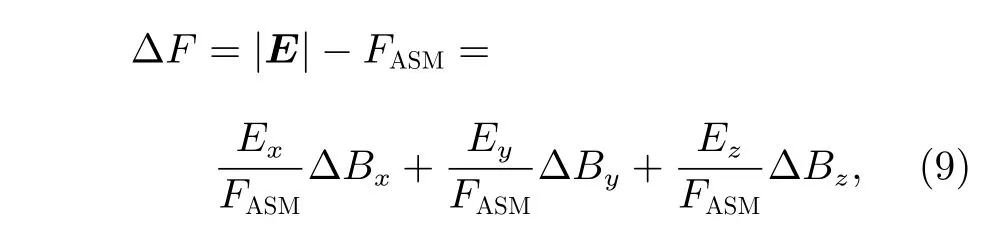
具体推导为
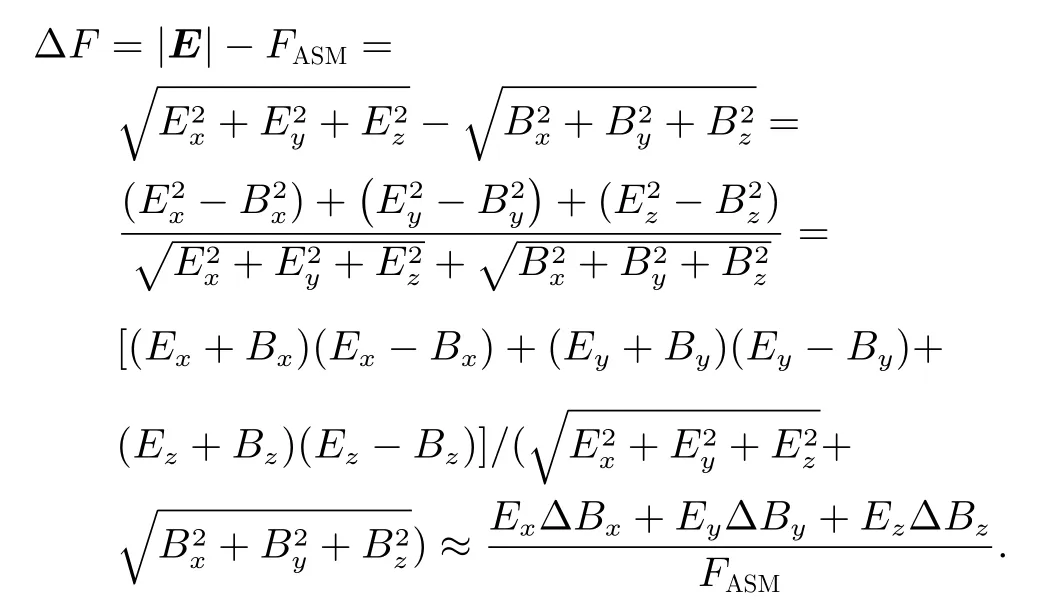
式中,FASM为标量磁强计测量的磁场标量值,具体表示为
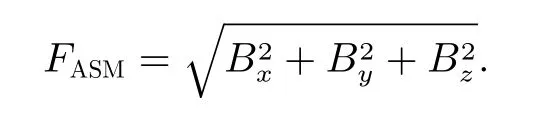
将式(8)代入式(9)中,标量残差可表示为矩阵形式
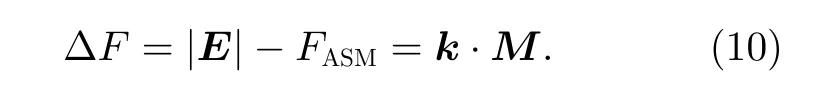
式中,k为待求校正参数矢量;M为磁场数据矢量,具体表示为
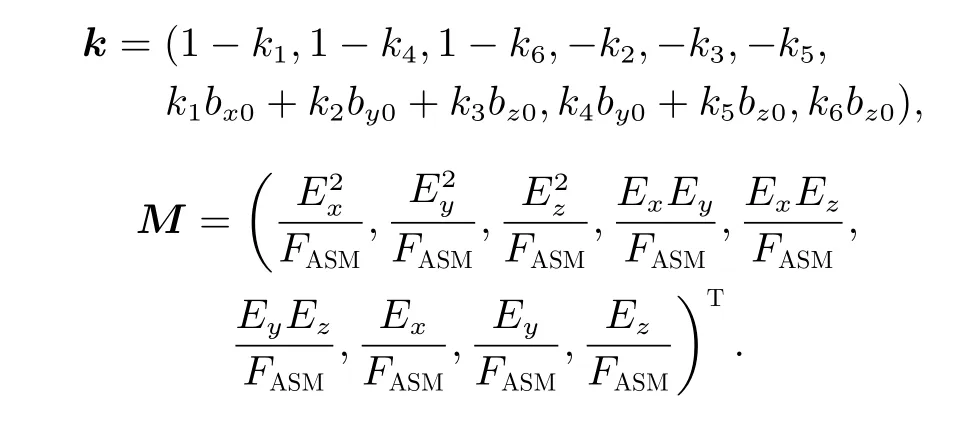
针对上述线性模型采用迭代重加权最小二乘(Iteratively Reweighted Least Squares,IRLS)算法实现。损失函数定义为
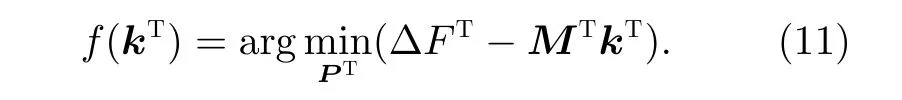
待求参数矢量为
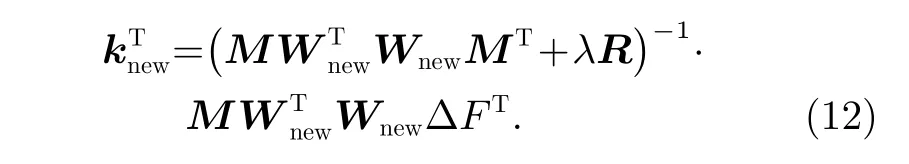
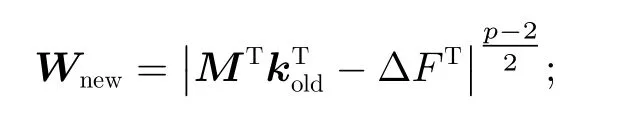
R为正则化项,减少迭代过程中由于矩阵奇异造成结果不准确的情况。通过适当选取参数p、正则化项以及迭代次数,实现损失函数的极小化。
2.2 基于参数辨识更新的非线性校正算法
基于参数辨识更新的非线性校正算法采用非线性最小二乘方法,从极小化磁场标量残差的角度出发,直接考虑非正交角、偏差以及标度因子矩阵对磁场测量的影响。相比线性校正算法中简化非正交性矩阵得到的线性校正模型,非线性校正算法直接对矢量磁强计的误差参数进行辨识更新,直接得到非正交角、偏差以及标度因子的校正结果。
由式(3)矢量磁强计处的磁场矢量,得到磁场标量表达式为[17]

式中,矢量磁强计标度因子、非正交角及偏差共9 个参数,可由参数矢量m表示,有
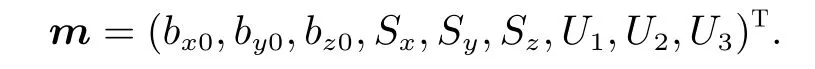
矢量磁强计与标量磁强计磁场测量的标量残差可以表示为

式中,δdk为第k次迭代的残差;Gk为Jacobi 矩阵;权重矩阵在每次迭代中更新,为对角阵形式。具体表示为
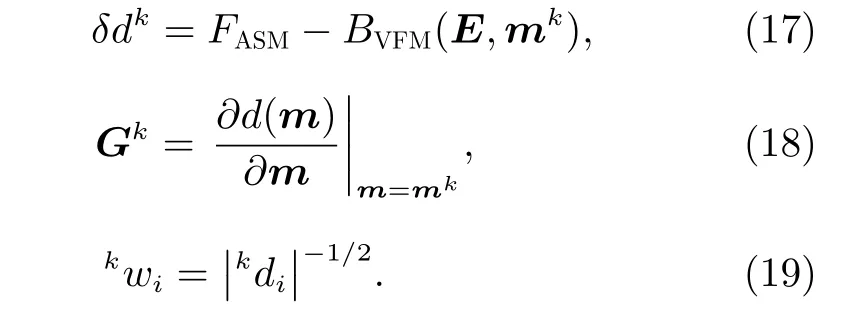
式中kwi为第k次迭代中权重矩阵的对角线元素,取决于第k次迭代中每个样本点对应的残差量大小。
3 仿真校验
3.1 仿真数据模拟
由于目前国际上SWARM 等卫星并未公开磁场探测的0 级数据,为验证本文算法的有效性,为中国后续高精度地磁测量卫星磁场标定提供参考,这里通过数学仿真的方式构造原始探测数据。由国际通用地磁场模型IGRF13 系数以及磁位函数的球谐表达式,建立地球磁场模型[18]。地磁位的球谐函数表达式为
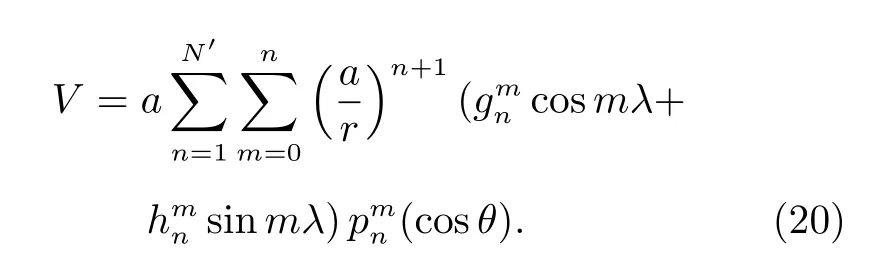
式中,a为地球半径,r为观测点离开地心的径向距离,θ为地理余纬;λ为 东经;(cosθ)为n阶m次的缔合勒让德函数;N′取14;和为地磁场球谐系数。图2 给出了全球地磁场仿真结果。
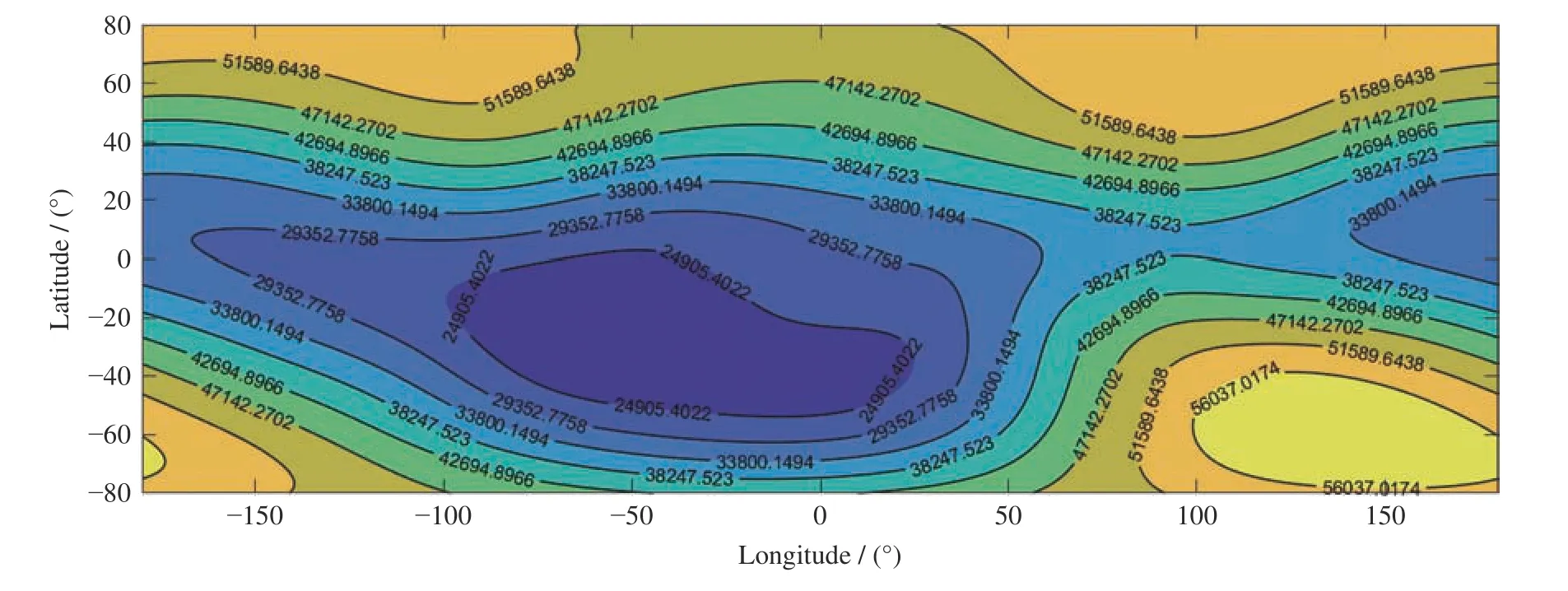
图2 全球等强度地磁分布Fig.2 Global geomagnetic map of equal intensity
针对某地磁测量卫星,轨道高度400 km,轨道倾角87.357°,升交点赤经297.019°,卫星轨道为圆轨道,考虑地球扁率摄动的影响。
假定标量磁强计与矢量磁强计初始采样频率均为50 Hz,标量磁强计测量值的固定误差设置为0.3 nT,其他仿真参数在表1 中给出。卫星本体坐标系定义为:O点位于卫星质心,Ox轴在轨道平面内指向速度方向,Oz轴指向地心,Oy轴垂直于轨道平面且与Ox和Oz轴构成右手坐标系。假设卫星本体系与矢量磁强计坐标系重合。
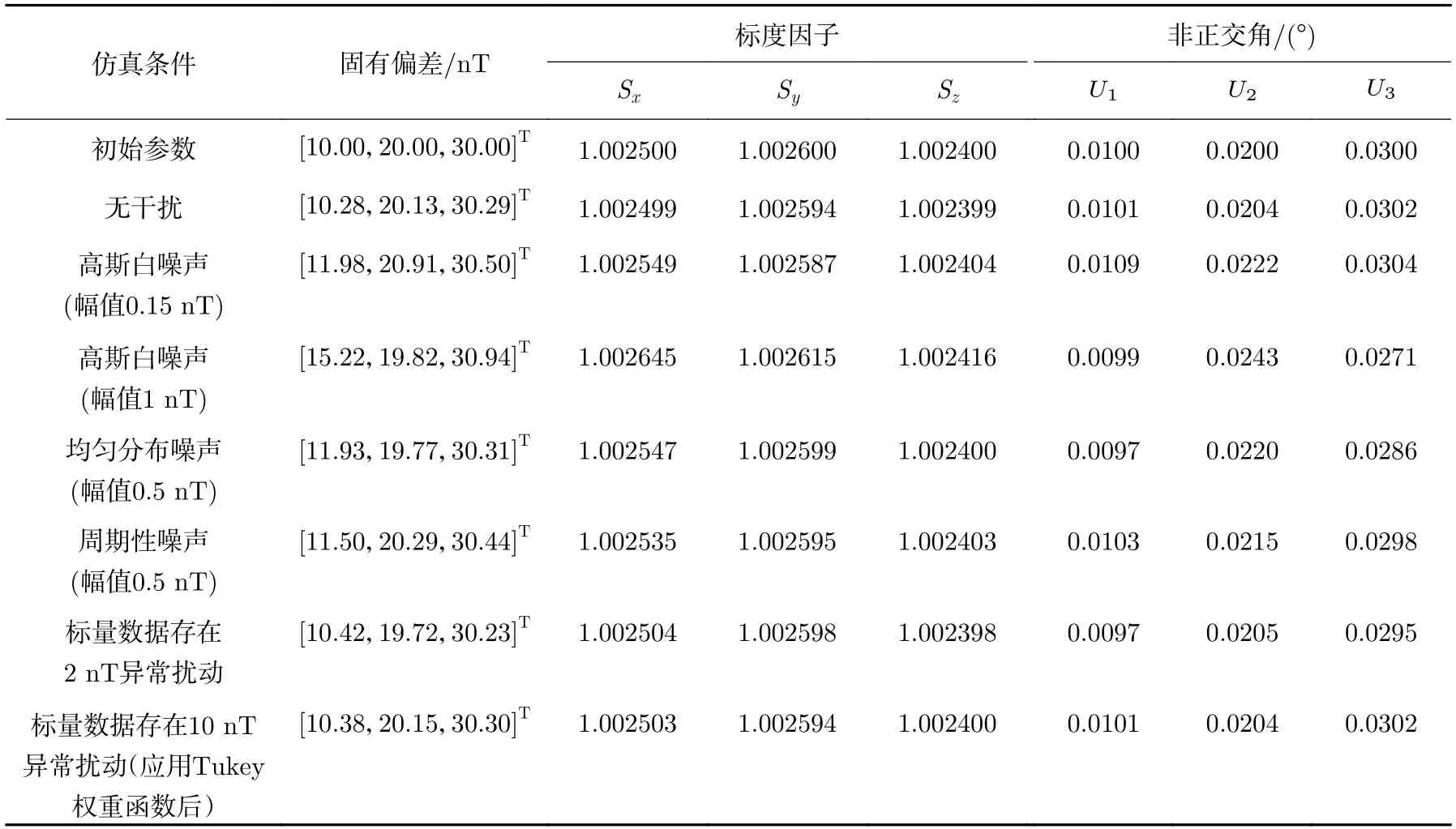
表1 不同情况下非线性校正算法参数辨识结果与初始参数对比Table 1 Parameter identification results of the nonlinear correction algorithm in different cases compared with the initial parameters
3.2 标量校正算法对比
在上述初始参数给定的情况下,研究引入传感器误差后两种校正方法的有效性。将两种校正方法进行对比分析,在仿真中不考虑其他磁场干扰的影响。
卫星本体坐标系下的磁场仿真数据(共计124000 组)如图3 所示。从图4 可以看出,传感器初始参数设置带来的x轴磁场测量误差最高达85 nT,y轴误差最高达98 nT,z轴误差最高达81 nT。
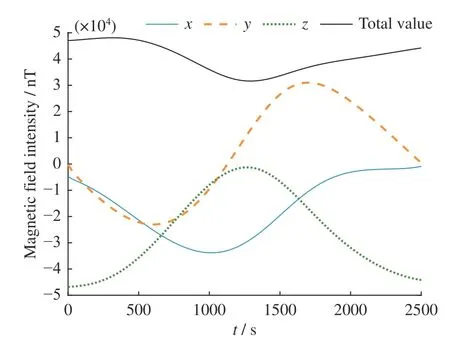
图3 采样频率为50 Hz 时的磁场仿真数据Fig.3 Magnetic field simulation data at sampling frequency of 50 Hz
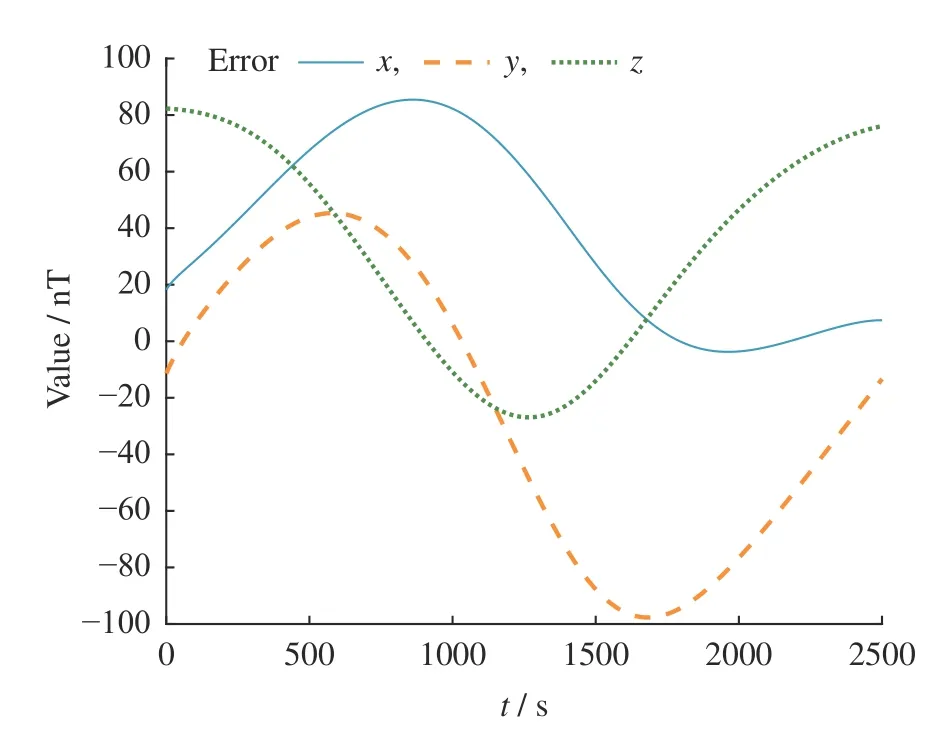
图4 三轴初始测量误差Fig.4 Initial measurement errors of the three axes
图5 表明,经线性校正算法校正后,三轴误差在±0.352 nT 范围内变化,标量残差在±0.0008 nT 范围内变化。图6 表明,经非线性算法校正后,磁场三轴误差在±0.341 nT 范围内变化,标量残差在±0.0007 nT 范围内变化。
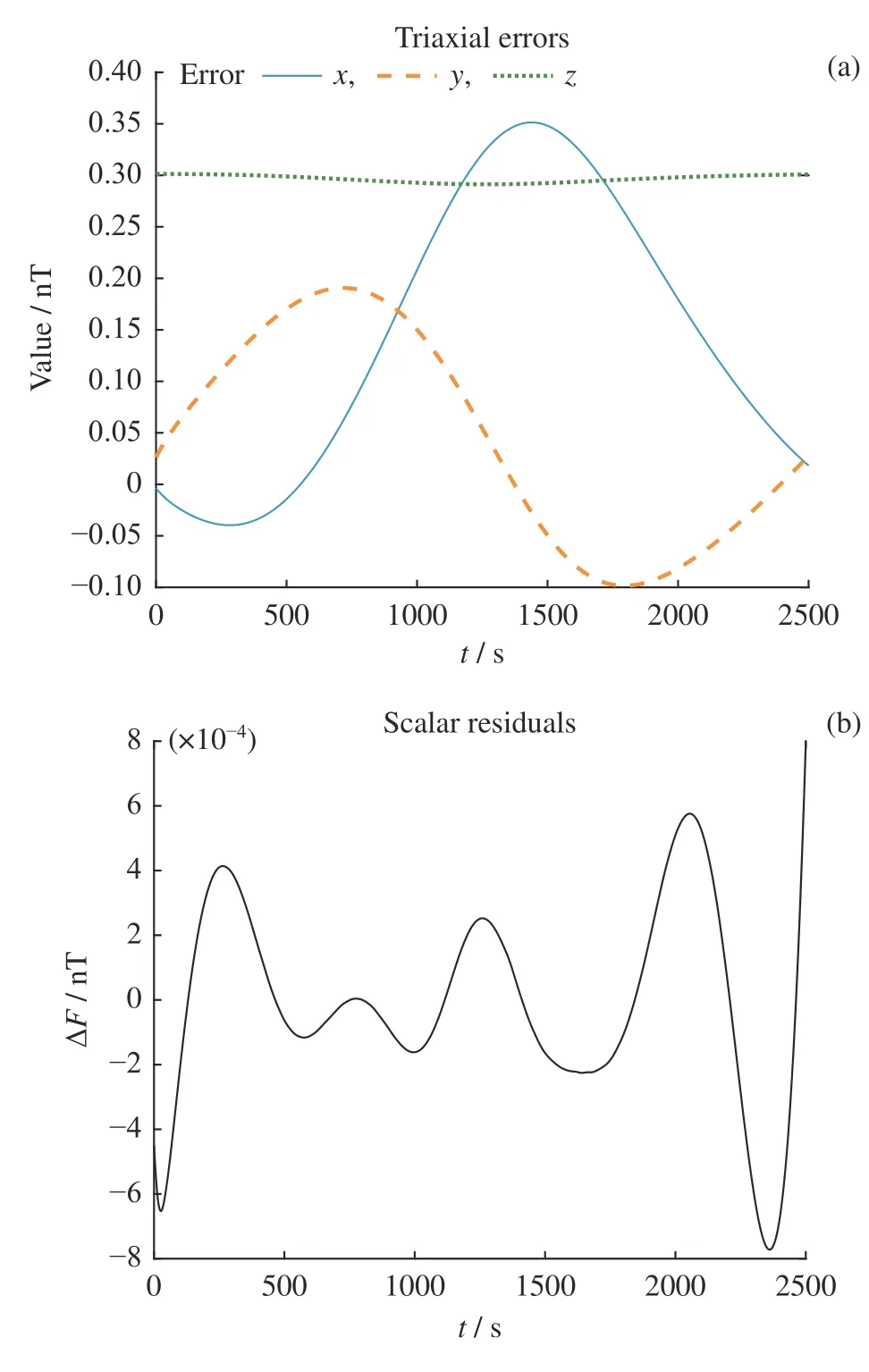
图5 经线性模型校正后的磁场三轴误差变化曲线以及标量残差Fig.5 Magnetic field errors and scalar residuals after linear model correction

图6 经非线性模型校正后的磁场三轴误差以及标量残差变化曲线Fig.6 Magnetic field errors and scalar residuals after nonlinear model correction
对比两种算法的校正结果,在考虑矢量磁强计非正交角、标度因子和偏差的影响下,两种算法校正结果基本相同。
基于小量近似的线性校正算法通过更新磁场矢量数据和误差模型参数实现校正效果,最终的辨识参数为校正后矢量磁场数据(误差<0.5 nT)对应的误差参数;基于参数辨识更新的非线性校正算法通过不断更新误差模型参数,使其逼近磁场矢量测量数据对应的误差参数,实现校正效果。
非线性校正后的传感器参数辨识结果列于表1,偏差量误差在±0.23 nT 以内,三轴标度因子误差保持在±0.000006 nT 以内,非正交角误差在±0.0004°以内,辨识后传感器参数均保持在较高精度。
3.3 噪声干扰情况下仿真对比
分析矢量磁强计不同形式测量噪声干扰对校正方法的精度影响。由于两种校正方法在噪声干扰情况下的校正结果相似,因此这里给出了非线性方法的校正结果。
添加幅值为0.15 nT 的高斯白噪声,校正后三轴误差由于受矢量磁强计误差的限制,其振荡幅值在±0.6 nT 以内。标量残差受噪声影响较大,其范围由±0.0007 nT 增大至±0.5 nT。添加幅值为1 nT 的高斯白噪声,三轴误差水平基本保持在±2.5 nT 以内。对比图7 和图8 可以看出,校正后三轴误差与标量残差的幅值均与噪声相关,表明噪声对传感器误差造成了叠加影响,标量残差受噪声影响较大。图9 给出了矢量磁强计存在幅值为0.5 nT 的均匀分布噪声和周期性噪声时,经算法校正后的三轴误差。结果表明,校正误差不受噪声形式影响,基本与噪声的幅值水平保持一致,误差分布与噪声具体分布相关。结合表1 不同形式的噪声干扰对比结果可以得出,参数辨识结果仅与噪声幅值相关,与噪声形式无关。
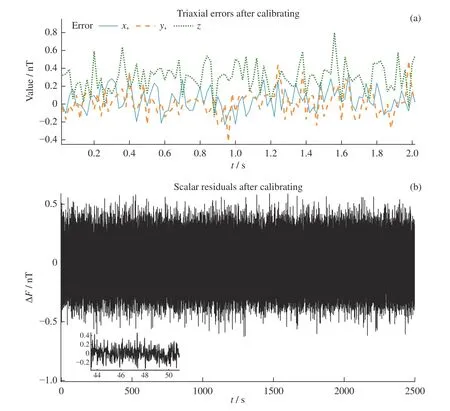
图7 添加幅值为0.15 nT 高斯白噪声干扰后的校正结果Fig.7 Calibrating results disturbed by Gaussian white noise which amplitude is 0.15 nT
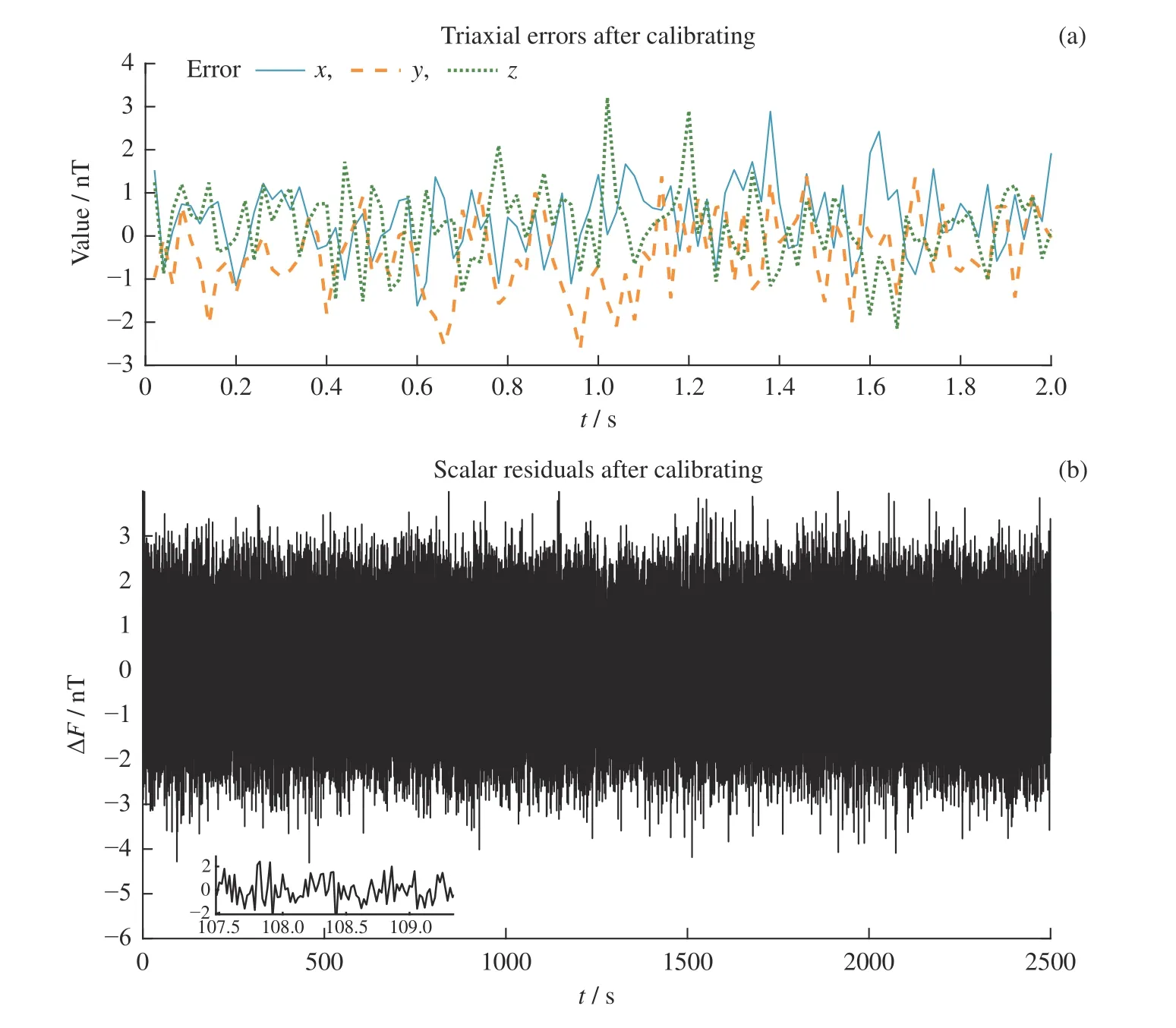
图8 添加幅值为1 nT 高斯白噪声干扰后的校正结果Fig.8 Calibrating results disturbed by Gaussian white noise which amplitude is 1 nT
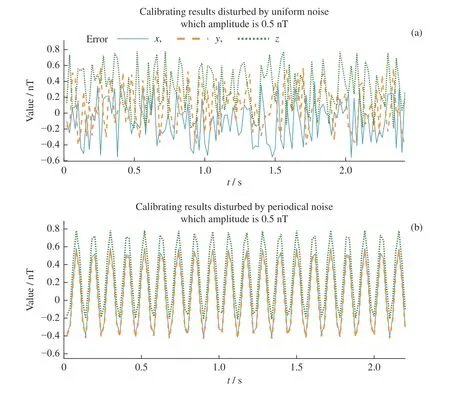
图9 添加幅值为0.5 nT 均匀分布噪声和周期性噪声干扰后的校正结果Fig.9 Calibrating results disturbed by uniform noise and periodical noise which amplitude is 0.5 nT
3.4 异常扰动情况下仿真对比
考虑标量磁强计测量过程中,可能由于数据处理单元电压的瞬变导致测量结果中出现异常值[19],同时考虑该异常体现在标量磁场测量值的瞬间突变,且无法通过数据预处理进行消除。这里针对磁场标量数据的异常扰动问题,对线性和非线性校正算法的处理结果进行分析。
在标量数据中添加单次大小为2 nT 的异常扰动,该异常扰动由瞬间脉冲仿真实现,矢量数据不受标量异常的影响。
由图10 可以看出,标量数据存在2 nT 的异常扰动时,对线性算法校正精度影响较大。考虑线性校正算法第k次迭代中利用k-1 次校正结果,将异常值造成的误差反复迭代,因此受标量数据异常值的影响较大。增大异常扰动至5 nT,非线性校正算法精度也受到影响。由于两种算法均通过最小化均方误差实现参数求解,扩大了异常值带来的影响。为提高算法的鲁棒性,将权重函数改进为Tukey 权重[20],有
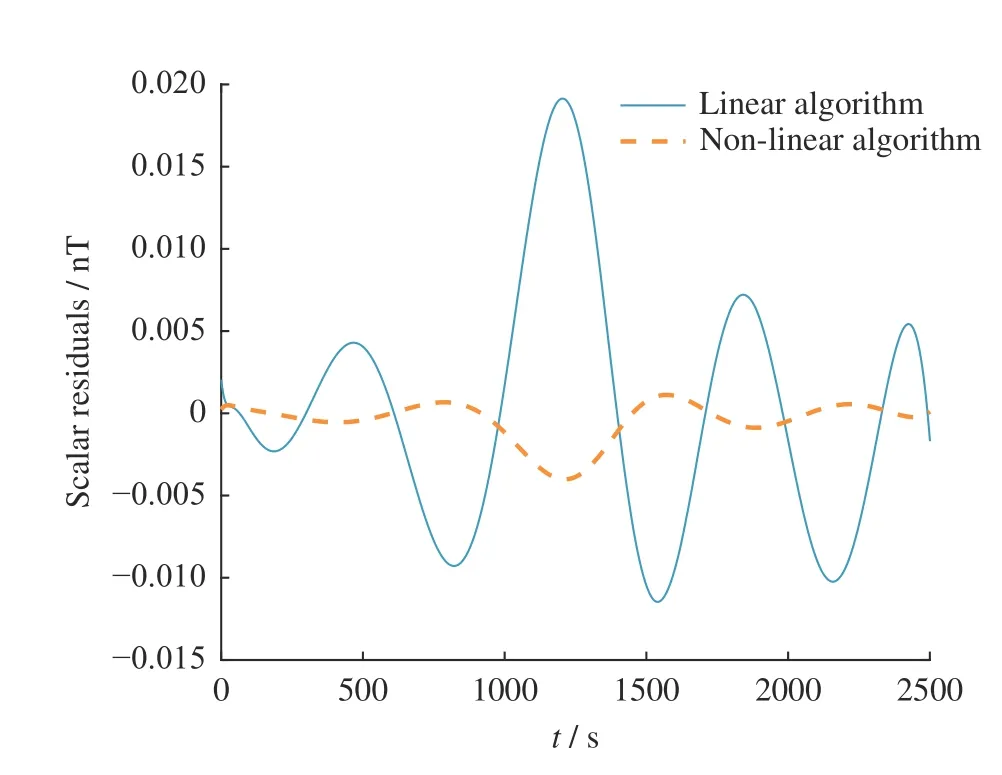
图10 标量数据中添加2 nT 异常扰动后的校正结果Fig.10 Calibrating results of scalar data adding 2 nT anomaly perturbation

式中,δi为数据残差,ε为定义异常值的削波函数。Tukey 权重函数通过削弱标量数据中异常值的权重,提高算法的鲁棒性。数据中的异常值由削波函数ε体现,当数据对应的拟合残差大于ε定义的阈值时,则视为异常值。Tukey 权重函数使异常值处权重为0,不参与算法运算,降低干扰。改进权重函数后,标量数据添加10 nT 的异常扰动,两种校正算法的标量残差如图11 所示,两种算法基本不受异常值的影响。同时,由表1 非线性算法参数辨识结果可以看出,权重函数的改进提高了非线性校正算法的参数辨识性能。这表明在应用Tukey 权重函数有利于提高算法的抗干扰能力。
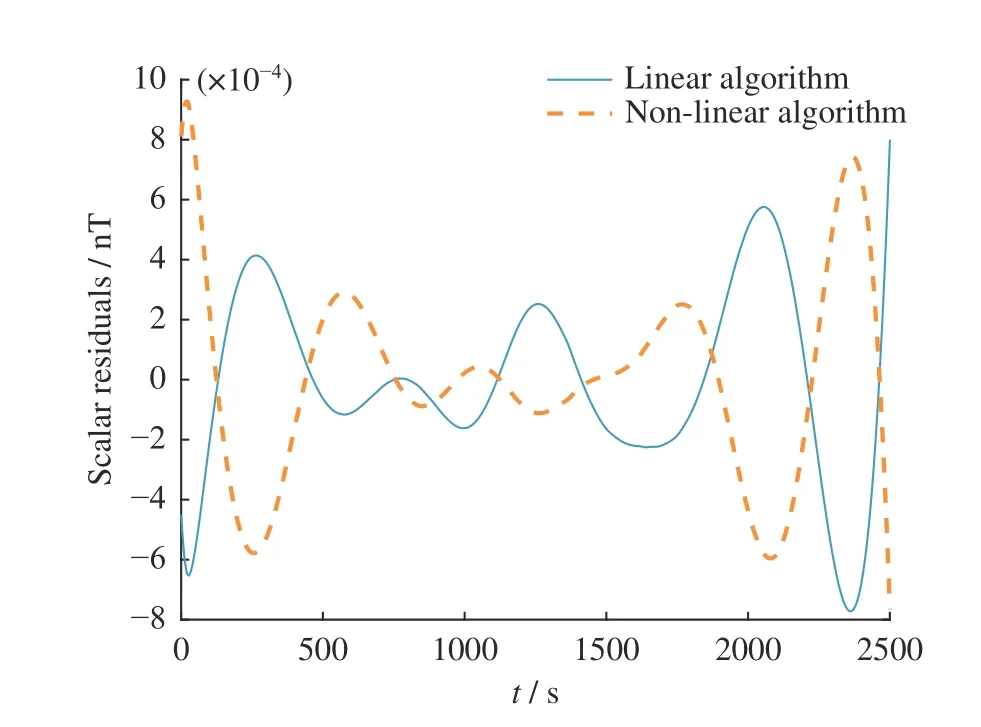
图11 标量数据中添加10 nT 异常扰动后的校正结果Fig.11 Calibrating results of scalar data adding 10 nT anomaly perturbation
4 结论
针对地磁测量卫星矢量磁强计测量误差的在轨标定问题,分别设计了基于小量近似的线性校正算法和基于参数辨识更新的非线性校正算法,仿真了传感器误差影响下的磁场测量数据,校验分析了两种磁场标定算法的效果。其中,基于小量近似的线性校正算法在考虑矢量磁强计非正交角均为小量的基础上进行设计,同时矢量磁强计的误差模型仅考虑非正交角、标度因子和偏差的影响,因此线性校正算法的近似是允许的。卫星在轨运行期间,由于不确定性因素引起的建模误差,对于小量近似的线性模型校正方法具有一定局限性。非线性校正算法从矢量磁强计误差模型参数辨识更新的角度出发,通过求解矢量磁强计误差参数矢量的Jacobi 矩阵实现磁场测量数据校正。相比线性校正算法,基于参数辨识更新的非线性校正算法的参数扩展性更强,更适用于复杂误差模型的磁场数据校正。
仿真结果表明,在考虑矢量磁强计标度因子、偏差、小角度非正交角的影响且矢量磁强计测量噪声幅值低于0.5 nT 的情况下,两种算法校正后的三轴误差均在0.5 nT 以内,非线性校正的辨识参数与初始参数误差在合理范围内,算法不受测量噪声的影响。同时,将算法中关于残差的权重函数改进为Tukey 权重函数提高了算法的鲁棒性,适用于地磁测量卫星磁场探测数据的在轨标定。研究结果可为中国张衡一号、澳门科学一号等高精度地磁测量卫星数据处理提供参考。
